基于“类比”思想下“三化”形式学习有效性探究——以《5.1分式》起始课为例

王冬平

(浙江省杭州钱塘新区学正中学 浙江 杭州 310000)

“类比”思想能够将一些抽象的知识转化为形象的概念帮助学生更好的主动理解知识点，将一些新知识转化为旧知识，这样学生能够更好地理解和接受，降低学生的学习难度，消除学生内心的畏难情绪，数学思维在这一过程中得以培养。[1]

分式是在学生学习了整式运算、因式分解的基础上进行的，是今后继续学习分式的性质、分式的运算及解分式方程的前提.本课是浙教版七下第五章起始课内容，本次课堂教学中运用类比思想结合“三化”形式能够有效改变原有教学模式的弊端，做到学有所得、学有所思。“三化”即化“被动”学为主动学；化“不动”学为“能动”学；化“机动”学为“思动”学。

1.目标与目标解析

笔者用整数的除法引入，目的是引导学生将整数类比整式，了解分式的形成。其次抓住运算这一核心，分离出分数的本质属性为分式的产生提供思路,最后引导学生用分式解决实际问题，充分体验数学源于生活又服务于生活。

2.学情分析与问题诊断

2.1 学生的数学基础。在本节课之前，学生已有了列代数式的经验，掌握了分数、整式的相关知识，但对于主动转换知识，不同情境下应用同类知识能力有所欠缺，缺乏同类知识迁移学习技巧。

2.2 学生的数学障碍。通过前期的测试调查，大多数学生虽接触过分式只是懂得解题的套路方法，对于为什么会存在分式无意义，如何让分式成为有意义以及如何让此分式值为零此类问题学生更多时候是知其然并不知其所以然。

3.教学过程设计

前测：对于学生整式学习进行简单摸底。

3.1 化“被动”学为“主动”学，循序渐进，获知概念。

活动1：任意选择两个整数，并对其进行相加、相减、相乘、相除运算，观察其结果是否仍是整数？

8+3； 8-3； 8×3； 8÷3

师生活动：探究任意两个整数相加、相减、相乘的结果都仍是整数，但是相除的结果不一定是整数。

抛出问题：两个整数相除，若结果不是整数，怎样规范的表示所得结果？(引导学生回顾用分数表示结果。)[3]

活动2：(小组合作，共同探索)任意选择两个整式，并对其进行相加、相减、相乘、相除运算，观察其结果是否仍是整式？

a+(2a+1);a-(2a+1);a×(2a+1);a÷(2a+1)

师生活动：引导学生通过计算发现，整式与整式相加、相减、相乘的结果仍为整式，但整式除以整式的结果不一定是整式。

抛出问题：分数使用来表示那些不能整除的结果，类比表示a÷(2a+1)的结果。

类比示意图：

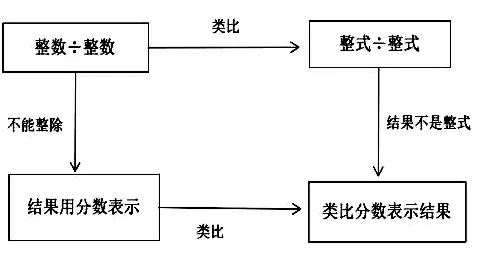
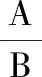
设计意图：在活动1，活动2两个过程中学生运用“类比”思想解决问题的同时，逐渐在脑海里建立“分式”的轮廓，这种轮廓意识的产生完全来自学生在课堂上结合两个活动的主动探索。

3.2 化“不动”学为“能动”学，类比整式求值尝试分式求值。

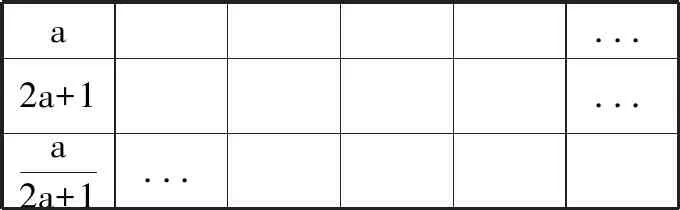
a...2a+1...a2a+1...

师生互动：通过上述的探究，你发现分式的值还有特殊的时候吗？

设计意图：通过活动3，学生以小组探究的形式，更加直观了解了分式的特性。

3.3 化“机动”学为“思动”学，从实际情景出发引发思考。“思动”学习形式是呼吁学生在深刻理解知识的基础上记忆知识并把握知识之间的联系，将知识迁移应用到实际问题情境中做出决策。

例题：

王珂和李明沿同一路线从学校出发去下沙宝龙城市广场，已知王珂每分钟走a米，李明每分钟走b米，如果李明提前2分钟走，王珂去追李明。

(1)若a>b那么王珂追上李明需要多长时间？

(2)当a=60,b=50时，求王珂追上李明所需的时间；

想一想，若a=50,b=50呢？(它所表示的实际情境是什么？)

设计意图：在实际生活中用分式表示问题中的数量关系时，不仅要保证分式本身有意义，还要保证字母索取的值符合实际背景。

课堂小结

课堂上学生们在小组合作中畅所欲言，模拟情境，结合本节课知识将自己投入角色中，获取了“分式”概念相关知识的同时又解决了实际问题。

【形成知识体系】

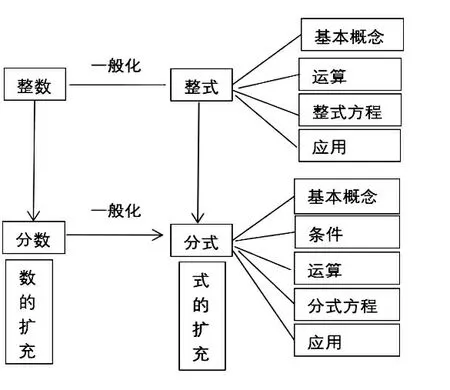
在同学们探讨补充中逐渐形成如上完整的知识体系，这一总结过程结合之前的课堂活动探索过程培养了学生自我整理的学习习惯，并指明今后探索学习的方向。

作业布置：校本作业A2，3,5，B6

设计意图：巩固并反思“分式”的形成，利用旧知识类比迁移新知识，打好基本功真正理解“分式”概念、有意义及求值。

4.课后反思——“三化”应用误区及有效化

并不是所有教材课本习题都是适用于任教班级学生，首先要了解本班学生数学基础，其次，思考要有长远化，对于数学知识的整体思考，并不局限于本节课或本单元，需拓展后期知识,教学上应考虑个体差异，对于基础好的学生可以引导他在不耽误学习进度同时进一步探索。

最后，需强调的是帮助学生建立“类比”思想意识并不是呼吁他们为了“类比”而“类比”，更不应设置看似热闹学生都“动起来”但对于本课或后期知识学习帮助不大的课堂探究环节，可以说，结合学情特点，设置合理问题、鼓励学生探索知识前后整体性是“三化”形式课堂需要抓住的重点。