基于AHP-隶属度函数的试制整车评价研究

肖璇 解嘉铖 赵新 韩野 潘禹澎

（一汽奔腾轿车有限公司奔腾开发院,长春 130013）

主题词：试制车 层次分析法 隶属度函数 整车评价

1 引言

汽车的产品质量是销量的基础保证，而试制车用于开发阶段动力总成匹配、底盘系统调校、电气系统标定和道路试验认可等，因此试制阶段产品质量直接影响整车开发。当前汽车产业正经历百年未有之大变局，行业发展面临前所未有的机遇与挑战，因此，为充分支撑新产品开发，实现自主品牌高质量发展，不断提升试制阶段产品质量显得极为重要。

为提升试制阶段产品质量，需要对试制车进行准确评价，并结合评价结果进行针对性改善。同时精准的整车评价还可以将不同项目的整车质量进行对比；将同一项目不同阶段的整车质量进行对比，并以此来准确判断整车质量是否提升。

本文构建了试制车全新评价指标，并基于层次分析法和隶属度函数法，确定评价指标权重并对整车状态和各指标状态进行实评研究，对装配制造质量改进提供重点方向，对产品设计变更提供具体思路。

2 试制样车评价指标及权重

层次分析法（AHP）是由美国匹茨堡大学教授运筹学家萨蒂所提出，其是把半定性半定量的问题转化为定量分析，核心是对评价指标通过1～9标度法进行两两比较确定相对重要程度[1]。

2.1 评价指标的选取

经过专家组多轮讨论研究，本文确定三级评价指标如下：一级指标为试制车整车状态[2]，整车状态主要考察5个二级指标，分别是内外饰状态、机舱和底盘、电气功能、走行和异音以及密封性。

（1）内外饰状态考察的三级指标为零件主体、零件表面、零件与对手件、操作与动作。

（2）机舱和底盘主要考察指标为机舱底盘间隙与干涉、部件支撑刚性、机舱底盘部件及其附件质量、油液/气泄漏。

（3）电气功能考察指标为锁与门窗系统控制与操作、灯光系统功能与控制、驾乘系统显示与控制、空调系统和音响娱乐系统。

（4）走行和异音考察指标为动力性、制动性、噪声与振动和操纵性。

（5）密封性考察指标为淋雨密封性和整车气密性。

2.2 评价权重的设定

样车试制过程大致分为3个阶段：骡子车阶段、工程样车阶段和OTS 车阶段，由于试制车不同于商品车，传统的Audit 评审是列举所有评审问题并进行分数累加，无需考虑权重，因此Audit评审适用于商品车或者预批量阶段车辆。试制车在骡子车、工程样车和OTS车阶段的车辆用途、功能要求和质量要求各不相同。

（1）骡子车是在产品开发初期，利用现有车型的白车身改装，由非生产工装制造的部件和总成试装出来的样车，用于零件空间的装配检查，以及汽车最初的性能数据采集、底盘性能测试、功能验证与认证，因此骡子车多关注其底盘性能，而内外饰状态权重则较低。

（2）工程样车是利用部分非生产目的的工装样件、软模件及平台共用件，进行车型首轮装配的样车，外观和内饰与量产车基本一致，用于检出与解决设计问题和装配问题，以及提供各项试验用车进行零部件/总成/整车的性能、可靠性验证和开发认证。所以工程样车权重与具体试验项目密切相关，如基础标定用车对内外饰，电气功能要求较低，而对走行性要求较高。

（3）OTS 车是利用生产工装样件装配的试装车，完全按照工艺要求标准、模拟量产环境，满足批量生产要求，不按生产节拍进行装配。用于验证品质问题和装配问题解决方案，和进行零部件OTS 认可路试，验证产品设计性能与可靠性。可见OTS 认可车的零件为工装件其要求与商品车接近，因此OTS车辆内外饰状态则需占有较大权重。

指标权重的确定方法有特尔斐法、熵权法、因子分析权数法、信息量权数法、独立性权数法、主成份分析法和层次分析法。因为层次分析法是国内外质量评价的主要手段之一并且应用较为成熟[3]，所以本文采用层次分析法计算指标权重。

2.2.1 评价矩阵的建立

评价矩阵的建立是通过1～9 标度法对评价指标进行两两互评，从而确定它们之间的相对重要程度。即评价指标之间的重要程度分为9个等级，aij=1、3、5、7、9 分别表征第i行元素比第j列元素同样重要、稍微重要、明显重要、强烈重要和极端重要，aij=2、4、6、8分别表征重要性位于上述相邻判断的中间。由此可见1～9 是2 者之间重要程度由低到高，并且评价矩阵为正互反矩阵。

本文以工程样车阶段基础标定车为例进行评价矩阵建立和实车评价并得到如表1 所示的二级指标评价矩阵和表2 至表6 所示的三级指标评价矩阵。

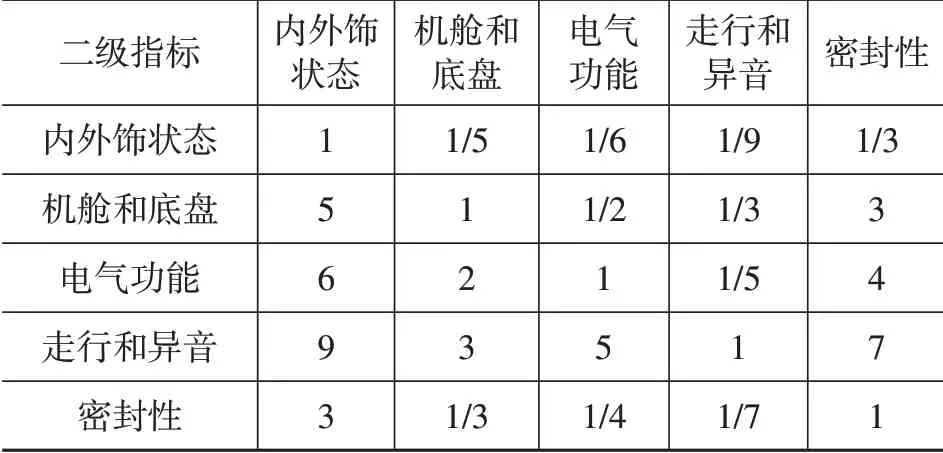
表1 二级指标评价矩阵

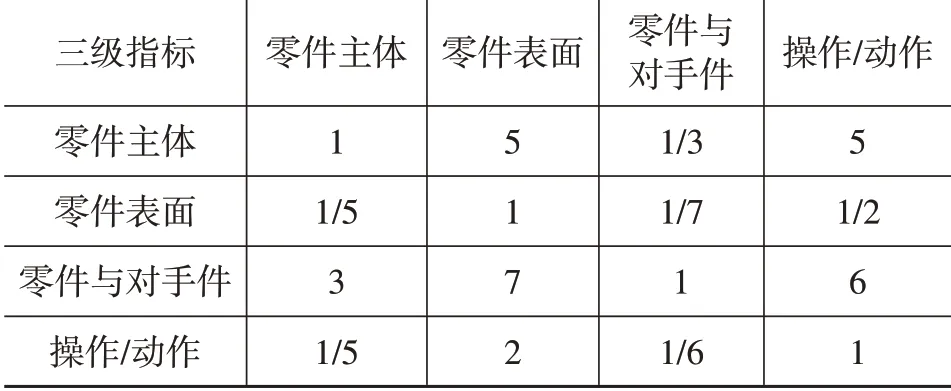
表2 三级指标评价矩阵

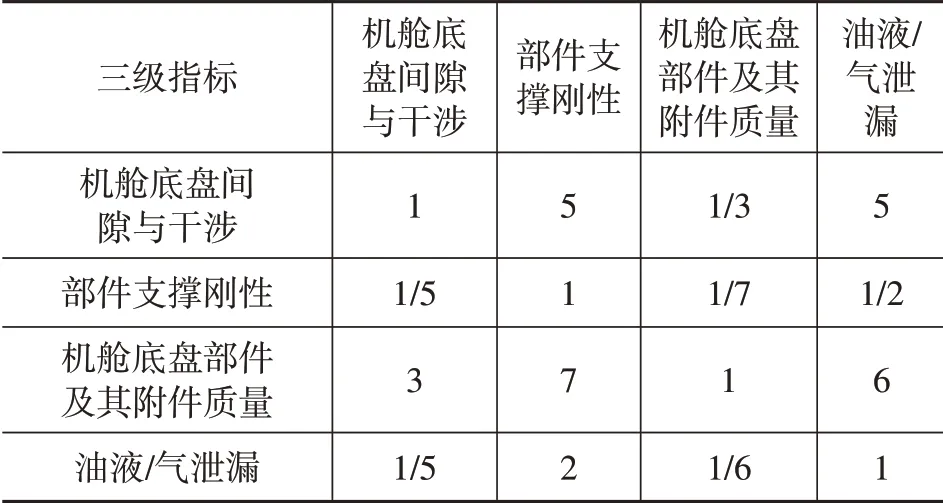
表3 三级指标评价矩阵

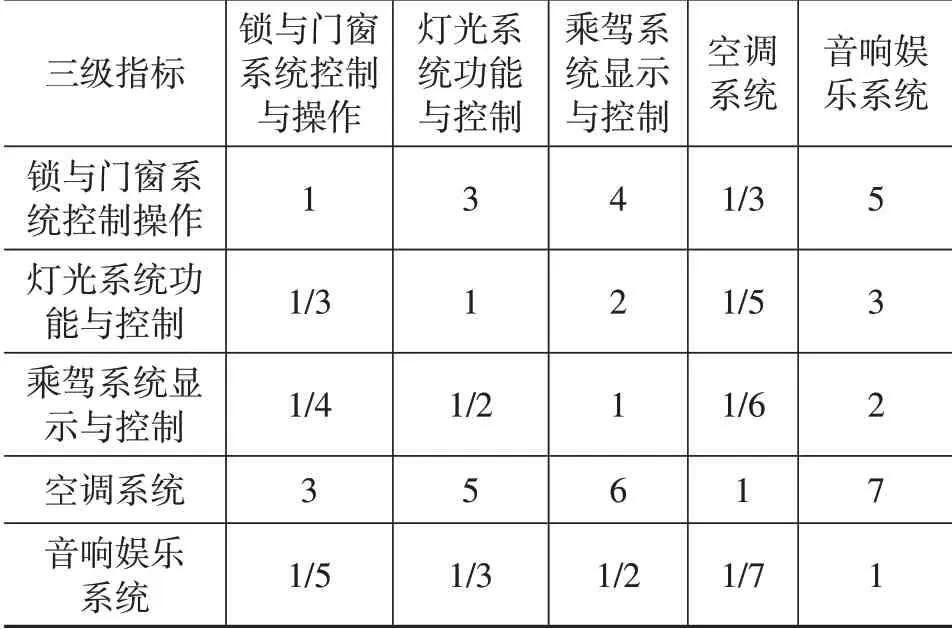
表4 三级指标评价矩阵

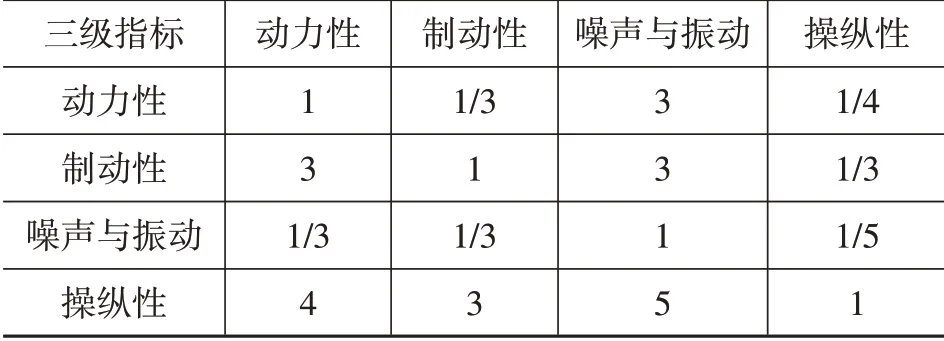
表5 三级指标评价矩阵

表6 三级指标评价矩阵

2.2.2 评价权重的计算

多数研究者为方便计算，采用均方根法求解。而当矩阵是一致阵时，矩阵的最大特征值所对应的特征向量即为权向量。所以当矩阵满足一致性条件时，最大特征值的特征向量可近似为权向量，记为W。因此，本文采用特征向量法并通过MATLAB 进行求解。矩阵一致性通过式（1）和式（2）判断。其中二阶矩阵必有一致性。

式中，RI为常数由矩阵阶数确定；λmax为矩阵最大特征值；n为矩阵阶数。

通过计算并通过式（3）将权值向量W归一化后可得二级指标各项权重Q为：

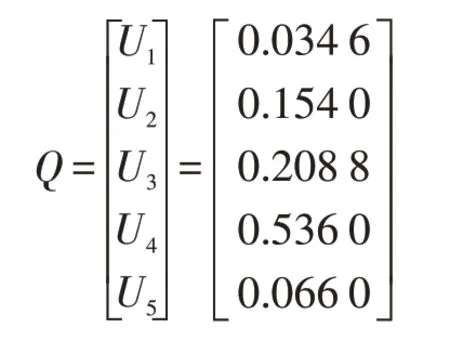
同理，通过计算并归一化后可得各三级指标权重Q1、Q2、Q3、Q4、Q5为：

3 试制车整车评价

3.1 隶属度函数的建立

隶属度函数的构造带有主观性，每个建立者都会建立不同的隶属度函数，但只要能反映和解决模糊评价的问题，隶属度函数的建立即是有效。构造隶属度函数的方法主要有模糊统计法、例证法、专家经验法和二元对比排序法。本文在专家经验的基础上初步建立粗略的隶属度函数，再经过不断的实践检验、修改和完善，最终得到如式(4)～(5)所示隶属度函数[4-6]。其中r1(x)、r12(x)、r3(x)、r4(x)分别代表评价为不合格、较差、良好和优秀的隶属度。

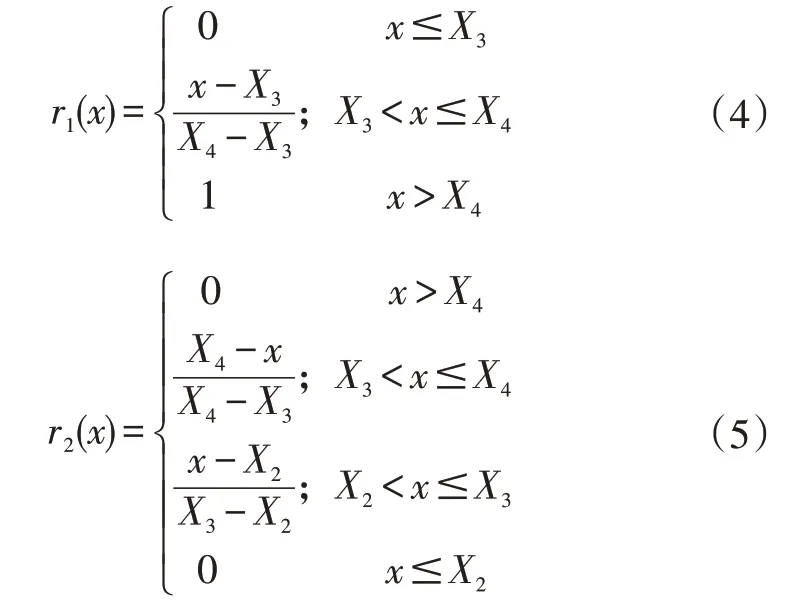
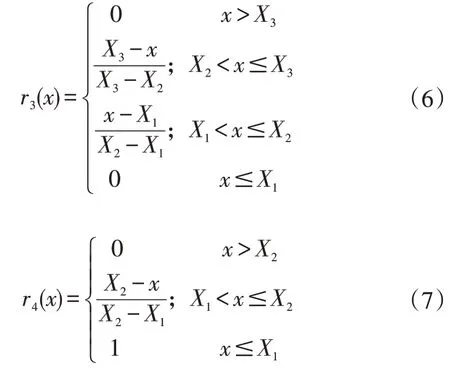
式中，X1、X2、X3、X4为评分阈值，本文取X1=0，X2=10，X3=120，X4=250，得如图1 所示函数图像。

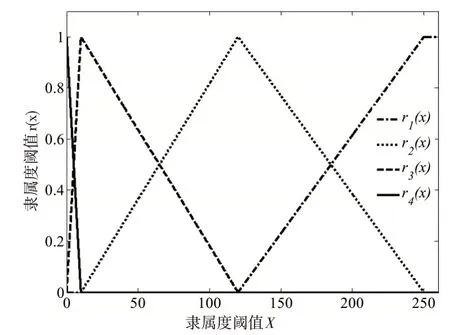
图1 隶属度函数

3.2 N项目试制车状态

N 项目为某自主品牌一款B2B 纯电动乘用车，是传统汽车制造商向移动出行服务公司转型的重要战略车型。本文的评价步骤为首先专家组现场评审并进行评审问题汇总。将评审问题按严重程度分为三级，其中Ⅰ级问题赋10分，Ⅱ级问题赋5分，Ⅲ级问题赋1分，通过各指标总分数代入隶属度函数，便可得到各三级指标隶属度矩阵。

通过对N 项目试制车进行评价并计算隶属度函数得到如下隶属度矩阵。

根据最大隶属度原则可见零件主体和零件与对手件两项指标处于较差状态，零件表面和操作/动作两项指标处于良好状态。同理可知其余三级指标状态都为良好和优秀状态。

根据公式Bi=(i=1、2、3、4、5)，可得二级指标评价评语矩阵R。

由评语矩阵和最大隶属度原则二级指标内外饰状态处于较差状态，其余二级指标均处于良好状态。

同理根据公式B=QTR，可得一级指标评价评语矩阵。

由此可见，虽然内外饰状态较差，但试制车整车状态为良好状态。这是因为基础标定用车对内外饰的需求不高。同时为提升质量可将权重较高的走行和异音进行重点改善。

4 结束语

本文首先确定了试制车三级评价指标，并通过层次分析法确定各指标权重，然后结合某N项目具体实车进行整车评价，并通过隶属度函数法判断三级指标状态隶属度，最后通过各级指标权重和隶属度计算得到试制车整车状态。

研究发现层次分析法结合隶属度函数法可以让主观评价更具客观性，更加适用于非商品车质量评价，既可以为质量提升提供重点改善方向，也可以量化整车质量，为通过项目节点决策提供数据支撑。

此方法在试制领域的应用仍未达到Audit评审和NOVA-C评审在商品车领域的成熟度，评价指标和隶属度函数仍需要工程师和研究者不断完善。