基于元学习的航空电子设备特征选择算法推荐方法

2021-07-05李睿峰许爱强孙伟超王树友

系统工程与电子技术 2021年7期

李睿峰, 许爱强, 孙伟超, 王树友

(海军航空大学, 山东烟台 264001)

0 引言

在航空电子设备故障诊断中,由于测试项目众多,导致原始数据维数较高,需要消耗大量的运算时间与存储空间[1]。因此,如何去除冗余信息和不相关特征,对测试数据进行约简,是航空电子设备故障诊断研究领域的一个基本问题[2-3]。

近年来,特征选择一直是一个活跃的研究领域[4],一个好的特征选择算法可以有效提取数据集中的关键信息[5-6]。文献[7]在电子电路故障诊断中使用粗糙集约简冗余特征。文献[8]提出了一种考虑特征相关性构成的特征选择算法。文献[9]将粒子群优化方法应用于特征选择过程。文献[10]将超限学习机技术应用于特征选择过程。文献[11]研究了基于K-means聚类的特征选择算法。

现有的特征选择算法通常都是针对某一具体应用而开发的,在特定的学习任务上表现出了优于其他算法的性能,但这不能表明该算法总是“优越”的[12],不同的特征选择算法可能会偏向于不同的数据集。因此,为了确定哪种特征选择算法对当前任务最有效,需要事先发掘这些算法对于各类数据集的适用情况。

元学习是一种利用以往知识经验来为新任务推荐有效学习算法的方法,目前已经在数据挖掘领域得到了广泛的应用。通过元学习,可以提取历史数据集和学习算法的元特征[13],在新的学习任务到来之时,结合与当前数据集最为相近的历史数据集上各类算法的性能,推荐有效的学习算法[14]。因此,建立一个用于特征选择算法推荐的元学习系统,可以直接为给定的故障诊断任务寻找最佳算法,有效避免因遍历所有特征选择算法导致的计算时间和空间上的开支。

此外,由于航空电子设备大部分时间处于正常状态,历史数据中故障样本贫瘠,数据集具有严重的类别不平衡特点。因此,建立的特征选择算法推荐系统应该能够更好地适应数据集不平衡这一特点。

综上,提出了一种基于元学习框架的航空电子设备特征选择算法推荐方法。首先,分析了采用基于统计和信息论的元特征来描述历史数据集的方法;然后,提出了考虑分类精度、查准查全率(precision recall curve, PRC)面积、算法运行速度和选择特征数量的综合指标,用于评价算法性能;最后,给出了特征选择算法推荐方法的框架,以及对于新数据集的算法推荐过程。采用了自动测试系统(automatic test system, ATS)日常维护中采集到的42种航电设备的测试数据,结合13个过滤型特征选择算法建立了元数据库,采用留一法进行了交叉验证。

1 元数据库建立

根据前文分析,特征选择算法在给定数据集上的性能和数据集特征密切相关。因此,建立元数据库首先需要对数据集特征(元特征)进行提取,并明确用于衡量算法性能的评价指标。

1.1 元特征提取

高质量的元特征[15]才能保证为新数据集推荐的特征选择算法更加合理。典型的元特征包括基于统计和信息论的元特征、基于基准分类器的元特征和基于模型的元特征等[16-19]。其中,基于统计和信息论类型的元特征被广泛采用[12]。基于统计和信息论的元特征又可以分为3类:一般元特征、统计元特征和信息论元特征。

假设具有N个样本的数据集表示为

(1)

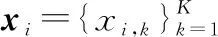
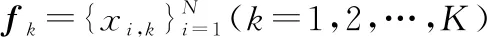
1.1.1 一般元特征

一般元特征用于概述数据集的基本信息,包括:① 样本数量N;② 特征维数K;③ 输出值数量M;④ 数据维度dim=K/N。

1.1.2 统计元特征

统计元特征用来表征数值型特征向量的统计学特性,包括各类特征的分布特性以及特征之间的相关性。这些特征主要有以下内容。

(1) 标准差:σ(fk)。

(3) 协方差

(4) 相关系数

(5) 偏度

(6) 峭度

1.1.3 信息论元特征

基于信息理论的元特征更适用于描述离散特征,由于从航空电子设备采集的测试数据集中每类特征在每个样本上都对应着独立的取值,因此可以应用信息论元特征。

特征向量fk的熵用于度量其随机性,表示为

(2)

式中:qi,k=P(xi,k)为特征向量fk对每个xi,k的取值概率。

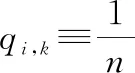
(1) 规范化类熵

式中:πm=P(lm)为每个类输出的取值概率。

(2) 规范化特征熵

(3) 联合熵

(4) 互信息

MI(fk,y)=H(fk)+H(y)-H(fk,y)=

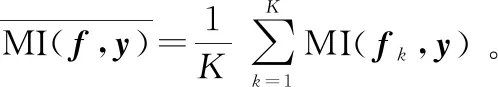
(5) 等价特征数

(6) 噪信比

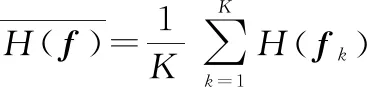
1.2 算法性能评价

一个算法性能的优劣,可以从多个方面进行评价,数据挖掘领域通常采用多标准度量指标。文献[20]结合学习算法准确性和总执行时间提出基于比率的多标准度量指标ARR多准则评估方法。文献[14]在此基础上针对特征选择算法推荐问题的特点,将选出的特征数量考虑在内,提出了EARR(extend ARR)多标准度量指标。这两种方法都采用了两个算法指标间的比值进行计算,以消除指标间量纲差异带来的影响。

航空电子设备面临着测试数据不平衡的问题[18],正常样本的数量常常是故障样本数量的几倍甚至几十倍,因此仅仅依靠分类精度来衡量算法的性能是不全面的。而且,故障样本的检测率在航空电子设备故障诊断领域中更有意义,也更为重要,因此本文在衡量算法性能时考虑了PRC面积指标。PRC是以查准率和查全率(基于混淆矩阵得出)为坐标轴绘制的曲线,曲线下面积的大小在一定程度上表征了学习器在查准率和查全率上取得相对“双高”的比例。在样本数量不均衡的数据集里,PRC面积更能有效衡量分类器性能的好坏。

在EARR多标准度量指标的基础上,进一步将PRC面积考虑在内,就可以得到一个综合指标，即算法Ai相比Aj在数据集Dk上的综合度量指数(multi-metric index， MMI):

(3)

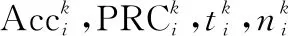
进一步,用算法Ai相比于其余算法在数据集Dk上MMI值的算术平均值表示算法Ai在数据集Dk上的MMI值:

(4)

式中:N为特征选择算法数量。

2 特征选择算法推荐方法

2.1 方法框架

明确了元特征和算法性能指标之后,就可以基于历史数据集建立元数据库,进而开发出用于特征选择算法推荐的元学习框架，如图1所示。其主要思想是利用元特征来描述数据集,并学习不同算法的性能;然后针对给定数据集与历史数据集的相似程度,利用元数据库选出合适的特征选择方法。

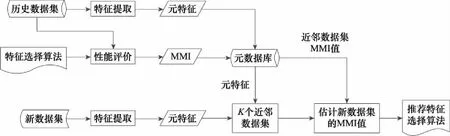
图1 算法流程图Fig.1 Algorithm flow chart

其中,元数据库由历史数据集的元特征和候选特征选择算法在这些数据集上的MMI构成。新数据集到来之时,根据元特征寻找其近邻数据集,推荐合适的特征选择算法。

2.2 推荐过程

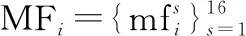
(5)

由于欧几里得距离是数据挖掘领域常用的衡量数据集之间距离的指标,因此新数据集Dnew和历史数据集Di之间的距离就可以表示为

(6)

通过式(6),可以找到新数据集Dnew的k个近邻数据集。如果dist(Dnew,Ds)=0,则视为Dnew与历史数据集Ds完全一致(这种情况的可能性极小,除非Dnew就是某个历史数据集),直接从元数据库中提取出候选特征选择算法在数据集Ds上的MMI值排序,作为推荐结果。

在dist(Dnew,Di)≠0的情况下,从元数据库中提取出候选特征选择算法在这k个历史数据集上的MMI值,利用Dnew和Di(i=1,2,…,k)之间的距离对其加权求和,则候选算法在Dnew上的综合指标可估计为

(7)

根据式(7),可以评估每个特征选择算法在Dnew上的综合指标,进而将候选算法根据估计的指标值进行排序。整个推荐过程可以表示如下。

步骤 1提取数据集Dnew的元特征,并运用式(5)进行归一化处理。

步骤 2根据式(6)计算Dnew和各历史数据集Di之间的距离,并将距离值从小到大进行排序。

步骤 3如果存在dist(Dnew,Ds)=0,直接从元数据库中提取出特征选择算法在数据集Ds上的综合指标排序,作为推荐结果。

步骤 4在dist(Dnew,Di)≠0的情况下,根据步骤2的结果找出Dnew的k个近邻数据集,运用式(7)估计候选算法在Dnew上的MMI值。

步骤 5使用估计的MMI值对特征选择算法进行排序,作为推荐结果。

3 实验分析

3.1 评价指标

目前尚没有统一的指标用来评价元学习方法的性能,但关注点通常在于衡量推荐结果与理想结果的差异性。文献[20]采用Spearman秩相关系数衡量算法推荐排序与理想排序之间的一致性,以评估推荐排序的质量。文献[14]采用了Friedman检验和Holm procedure检验判定各数据集上候选算法之间是否存在显著性差异,进而提出了推荐命中率这一评价指标。此外,文献[14]提出了推荐性能比例的概念,计算推荐算法与最优算法性能指标的比值,以衡量两者的接近程度。为了对特征选择算法的推荐结果进行有效评价,本文采用了推荐命中率和推荐性能比例两个指标。

(1) 推荐命中率

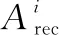
(8)

进一步,推荐命中率可以表示为

(9)

式中:G表示全部数据集的数量。

(2) 推荐性能比例

通过推荐命中率,可以判定推荐的算法是否有效。在此基础上,推荐性能比例能够进一步展示推荐的算法与最优算法在性能上的差距。推荐系统在数据集Di上的推荐性能比例表示为

(10)

3.2 实验设置

(1) 数据集

ATS在对航空电子设备日常维护中采集到的检测数据,对于内场维修中的故障诊断具有重要意义[18],因此本文采用了某飞行部队修理厂航电车间3年来对42个航空电子设备的检测数据建立元数据库。这些设备覆盖通信导航、显示控制、电子对抗等3个专业,各设备对应的测试项目和指标是根据履历本要求来确定的,测试结果包含布尔型、整型、浮点型等数值型数据。在检修过程中,如果遇到某个测试项目异常的情况,会通过返厂检查的方式确定其故障类别。数据集信息如表1所示。

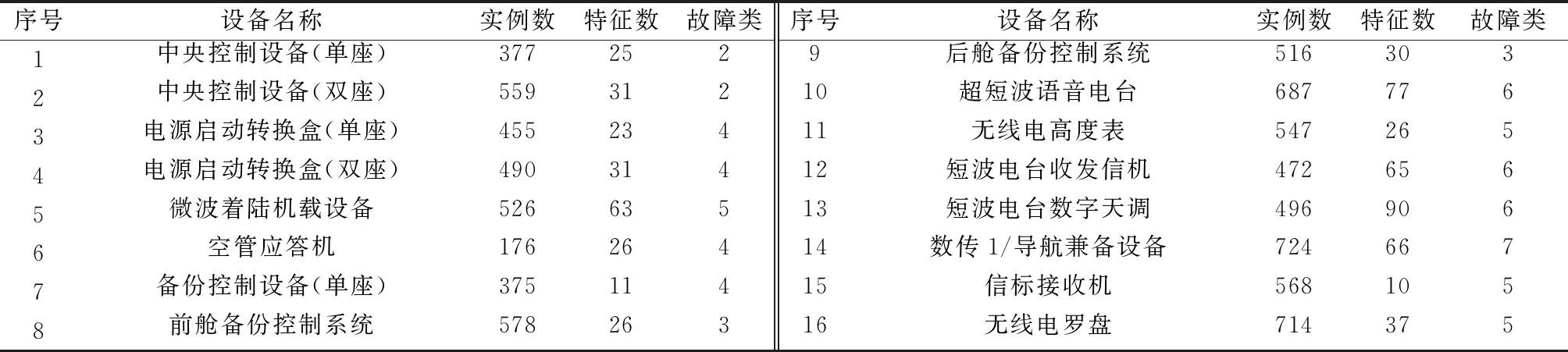
表1 航空电子设备数据集信息

续表1

ATS对设备施加的每个测试项目对应着数据集的一个特征。由表 1可以看出,这些数据集的特征数量从8 到229不等,实例数量从132到858不等。此外,由于航空电子设备大部分时间处于正常状态,因此设备历史数据中正常数据的规模远大于故障数据。实验采用留一法在这些数据集上对本文提出的特征选择算法推荐方法进行评价,并与计算MMI值时不考虑PRC面积的方法进行了比较。

(2) 特征选择算法

在Weka实验环境下,选择了13种特征选择算法。这些算法是不同搜索策略和评价方法的组合,是以往研究者为解决特定领域的特征选择问题而提出的,并且得到了广泛的应用。其中，搜索策略包括顺序搜索、遗传搜索[21]、秩搜索[22]、散射搜索[23]、禁忌搜索[24]等。评价方法包括相关性指标[25-26]、一致性指标[27-28]等。具体介绍如表2所示。

表 2 采用的特征选择算法

虽然Weka框架封装的特征选择算法远多于13种,但是其他算法(例如用于特征评估的算法[29],贪婪搜索策略[30]等)只能给出特征排序,需要通过设置阈值的方式选出子集,阈值设定会涉及到多方面因素,故没有将其作为候选算法。此外,新提出的特征选择算法都可以在Weka框架内实现。

(3) 分类器

由于不同的分类器内部机制不同,对特征选择算法的偏好程度也不同,为了对所提出的特征选择算法推荐方法进行客观评价,保证该方法并不只局限于某种类型的分类器,实验选择了4 种具有代表性的分类算法:基于决策树的C4.5、基于概率的朴素贝叶斯(Naive Bayes)、基于规则的 PART和基于实例(instance-based)算法(其近邻值设置为1，IB1)[14]。这些分类器代表了各自所属的类型,在以往的相关研究中被广泛采用。

(4) 参数设置

关于参数α和β对实验结果的影响,相关领域的研究人员已经进行了深入分析,在α和β取10%的情况下,推荐系统已经很大程度地偏向于推荐运行速度快且选出的特征数量少的算法。为了充分发掘参数α和β对推荐系统性能的影响,实验将参数α和β均设置为从1%到10%,以1%步长增长的取值序列,采用网格搜索法,以最大化推荐性能比例均值为目标,寻找最优参数设置。此外,文献[14]通过研究指出,k近邻值设置为历史数据集数量的28%到47%之间会取得较好的推荐效果,故本文将k值设置为15。

3.3 实验过程

针对每个数据集的特征选择和分类过程均在Weka3.8.4实验环境下进行,该阶段可以得到分类精度、PRC面积、特征数量、运行时间等实验结果。MMI值计算、确定最优算法集合、算法推荐和结果评价过程在MATLAB 2018a软件中运行。实验电脑配置为:Windows 10操作系统,Inter Core i7-7700HQ CPU,2.80 GHz主频和8 G RAM。具体实验过程如下。

(1) 建立元数据库

首先,按照第1.1节给出的公式,采集所有数据集的元特征。然后,在这些数据集上应用第3.2节列举的特征选择算法,通过 5×10 折交叉验证,收集分类精度、PRC面积、运行时间、特征数量等指标值,根据式(3)和式(4)计算MMI值。最后,将每个数据集的元特征和MMI值组合为二元组,添加到元数据库。此处将5×10 折交叉验证的结果分别计算MMI值,用于后面最优算法集合的确定,取其均值添加到元数据库。

(2) 确定最优算法集

对于数据集Di,前面的计算中得到了50 组 MMI值。由于这些指标数据通常不能满足正态性以及方差齐性,因此选择非参数假设检验的Friedman检验来确定每个数据集上 13个算法是否存在显著性差异。如果检验结果显示这些算法的性能不存在显著差异,那么这 13 个特征选择算法均被加入到最优算法集合中。否则,在此基础上进一步进行多重比较,将MMI均值最大的算法作为最优算法,挑选出其余算法中与之没有显著差异的算法加入到最优算法集合中。

(3) 算法推荐及结果评价

将每个数据集Di依次作为测试数据集,其余41个数据集构成元数据库。首先,根据当前数据集Di的元特征,按照式(6)从元数据库中识别出其k个近邻数据集。然后,基于式(7)和k个近邻数据集上的MMI值,估计各特征选择算法在Di上综合指标MMI值,并将这些估计值进行排序。最后,利用第3.1节中给出的评价指标对推荐结果进行评价。

为了确定最优参数组合,实验过程中需要根据第3.2节设定的参数α和β取值范围,重复计算MMI值,并根据推荐结果计算推荐性能比例均值。以取得最大推荐性能比例均值的α和β值作为最终的实验参数。

3.4 结果分析

受文章篇幅限制,不再对参数寻优过程作详细描述,只在实验结果中备注了最终参数取值。

3.4.1 推荐命中率

在42个数据集上推荐排名第1位的算法如图 2所示。4个子图分别为4个分类器上的结果,“○”表示推荐命中,“×”表示推荐未命中。不考虑PRC面积指标的算法推荐结果如图3所示。

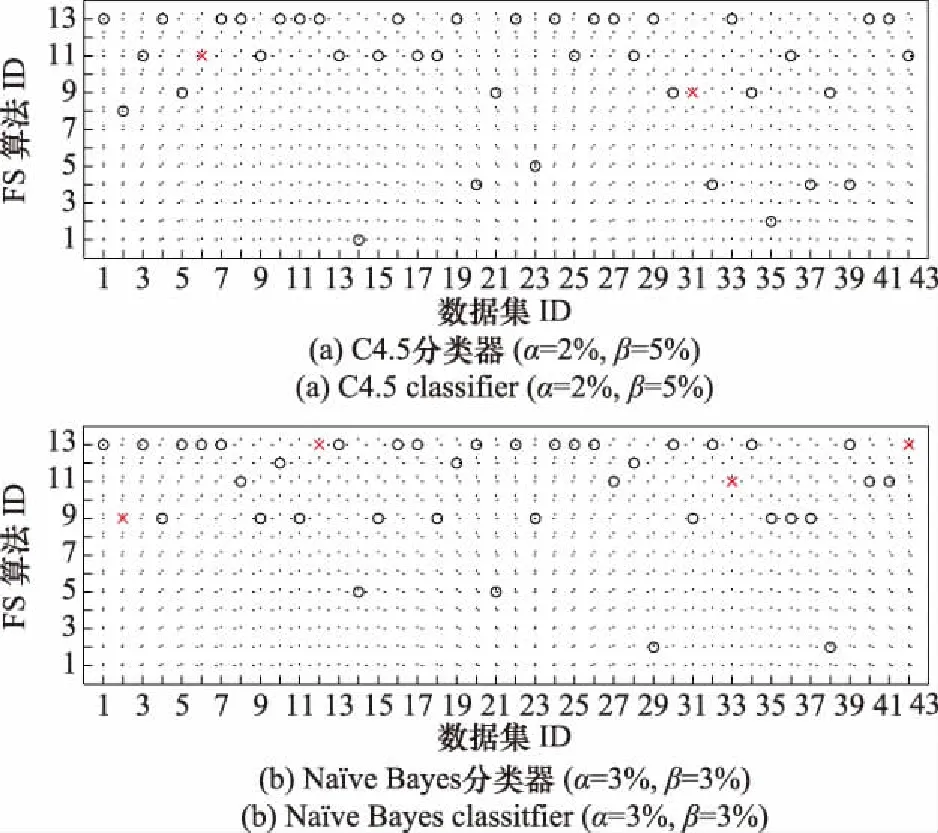
图2 算法推荐结果Fig.2 Algorithm recommendation results

在MMI值不考虑PRC面积的情况下,推荐结果如图3所示。

图3 不考虑PRC面积指标的算法推荐结果Fig.3 Algorithm recommendation results without considering PRC area index

根据图2和图3的结果,结合式(8),可以得到推荐系统在各个数据集上的推荐命中情况。进一步,运用式(9),可得两种方法的推荐命中率,结果如表3所示。

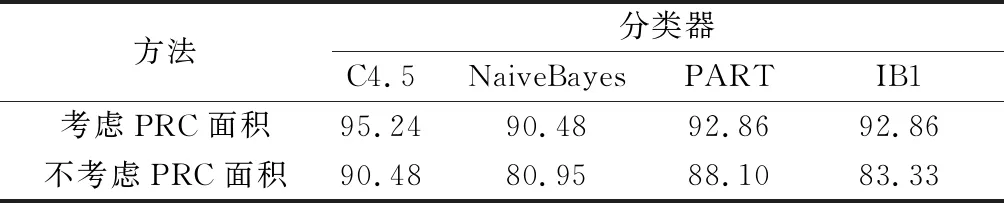
表3 推荐命中率对比

由图 2、图 3和表 3可以得出以下结论。

(1) 本文提出的特征选择算法推荐方法能够为42个数据集中的大部分推荐合适的算法。在选用的4个分类器上,均取得了较高的推荐命中率,分别为40、38、39和39个数据集推荐了最优的特征选择算法,说明该方法的泛化性能较好。另外,所提方法为每个数据集推荐的特征选择算法各不相同,说明为数据集推荐最合适的特征选择算法是非常必要的。

(2) 采用C4.5分类器的情况下推荐命中率最高,只有2个数据集没有推荐命中,说明决策树类的分类器对于处理当前问题更有优势,在具体应用中建议采用决策树类的分类器,为特定数据集推荐特征选择算法。

进一步,将排名前两位、前三位的算法作为推荐结果,如果其中至少有一个算法与最优算法无显著差异,则表明推荐命中,结合式(8)确定推荐命中情况,进而运用式(9)计算推荐命中率,结果如表4所示。

从表4可以看出,以排名前三位的算法作为推荐时,推荐命中率已经达到一个相当高的水平,因此可以将实验输出设置为推荐排名前3位的算法。

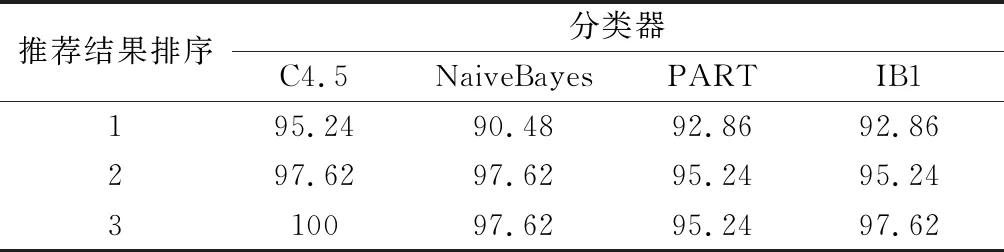
表 4 推荐命中率对比

3.4.2 推荐性能比例

根据式(10)计算排名第1算法的推荐性能比例如图4所示。

图4 不同分类器推荐性能比例Fig.4 Recommendation performance ratio of different classifies

在不考虑PRC面积的情况下,推荐性能比例如图5所示。由于在计算综合指标时考虑PRC面积会进一步增大不同算法间MMI值的差距,因为不考虑PRC面积相当于统一认定算法间PRC面积的比值为1。为了消除这种影响,实验中计算推荐性能比例时,根据两种方法得出的算法排序,统一采用考虑PRC面积方法计算得到的MMI值来计算。

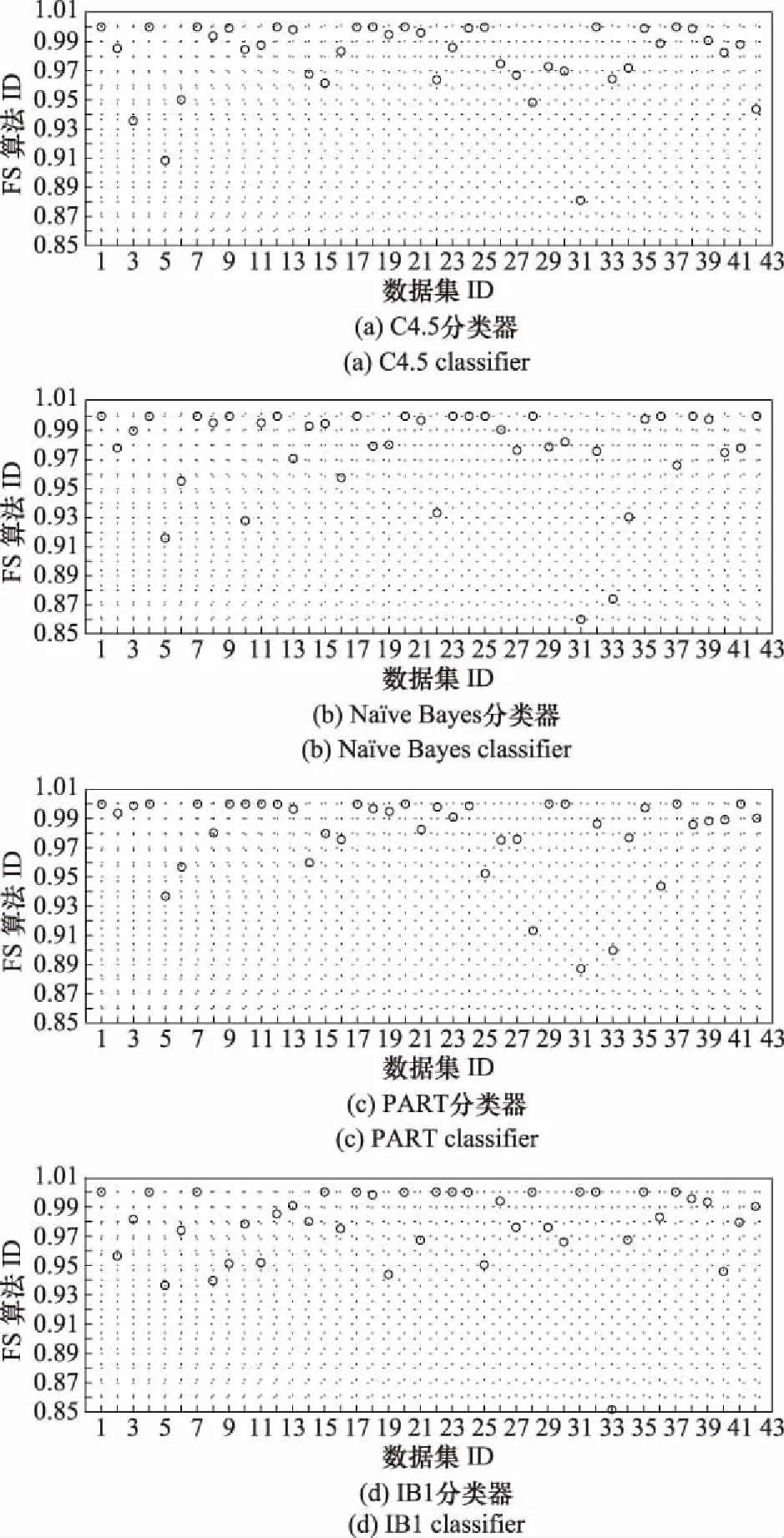
图5 不考虑PRC面积不同分类器的推荐性能比例Fig.5 Recommendation performance ratio of different classifiers without considering PRC area

进一步,计算4个分类器上的推荐性能比例均值,结果如表5所示。

表 5 推荐性能比例均值

由图 4、图 5和表 5可以看出,本文提出的推荐方法在4个分类器上的推荐性能比例普遍较高,最低值也高于93%。且在相当一部分数据集上,推荐性能比例为100%,表明经过推荐得到的算法与最优算法完全一致或者性能基本一致。相比较而言,不考虑PRC面积指标的算法推荐性能比例普遍低于考虑PRC面积指标的推荐方法,且推荐性能比例为100%的数据集也少于后者。

由于航空电子设备测试数据集具有显著的不平衡性特点,从表 5可以看出,考虑PRC面积的方法推荐结果更能接近最佳特征选择算法。这说明采用推荐的特征选择算法会取得较高的MMI值,实际上最终选出了哪些特征并不重要,因为MMI值高的特征选择算法能够更好地兼顾诊断精度、PRC面积这些正面指标和运行时间、特征数量这些负面指标,必将对后续的故障诊断产生有利影响。

当前应用于修理厂的ATS大多数只具备对航空电子设备的测试功能,部分ATS可以进行简单的故障诊断,而缺乏对测试数据的深入分析和处理。本文提出的特征选择算法推荐方法可以封装到ATS,在日常的检测和维护过程中,将采集到的测试数据提取元特征并添加到元知识库中,在有紧急需要的情况下调用推荐方法,为当前故障诊断任务推荐合适的特征选择算法,在保证后续故障诊断精度的前提下进一步提高效率,同时又能兼顾航空电子设备测试数据不平衡的特点。