基于概率测度的确信可靠性建模与分析方法

2021-07-05李泊远

系统工程与电子技术 2021年7期

李泊远, 康锐, 余丽

(北京航空航天大学可靠性与系统工程学院, 北京 100191)

0 引言

经过较长时间的发展,国内工业领域逐渐认识到可靠性系统工程的重要性。对于企业的可靠性工程,基本的故障归零模式[1]得到了比较广泛地运用,即发现故障、反馈信息、进行改进与验证。对于可靠性要求较高的企业会在设计、生产阶段组织多项可靠性试验,如环境筛选试验、可靠性验收试验、强化试验等,推广试验把关的可靠性应用模式[1],旨在正式交付之前通过改进设计或筛选的方式提高产品可靠性。

然而,上述可靠性应用模式主导的可靠性工程存在以下两方面的问题:

(1) 可靠性工程师在产品设计完成后进行设计失效模式与影响分析(design failure mode and effects analysis， DFMEA)等工作,仅仅是对原有设计的分析与优化,无法在产品设计之初就对系统进行正向设计,无法在产品的设计研发阶段采取措施提高产品可靠性;

(2) 在产品的设计生产过程中,对设计因素与环境因素中存在的不确定性缺乏认知,无法准确定量度量在实际情况下不确定应用场景中产品的可靠性。

为了解决上述可靠性工程中存在的问题,定量描述产品的性能变化与不确定性,以便在产品设计阶段提高产品可靠性,Kang等人提出了确信可靠性理论[2]。确信可靠性理论遵循可靠性科学最基本的3个原理:裕量可靠原理、退化永恒原理和不确定原理[3]。对于这3个原理,可以用以下3个方程来表示。

裕量方程:M=G(P,Pth)>0

(1)

(2)

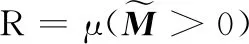
(3)

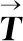
当研究对象的检测数据量大时,对于不确定性的度量,主要考虑确定性模型中参数的分散性,即固有不确定性。固有不确定性反映客观世界固有存在的随机特征,可以用概率测度进行度量[2]。在新产品的设计过程中,由于缺乏可用数据、对故障机理认知不足、缺乏单元内在关联机理认知等原因,会产生概率测度不适用的认知不确定性[4],可基于不确定理论采用不确定测度[5]进行度量。对于固有不确定性与认知不确定性相结合的情况,可采用机会测度进行度量[5]。

为了将确信可靠性理论转化为实践可行的可靠性设计流程,本文提出了基于概率测度的确信可靠性建模与分析方法,并以某型电连接器作为案例进行展示。本文为可靠性设计工作进行了创新性的理论探索和工程实践,为产品可靠性水平以及企业可靠性系统工程能力的提升起到了指导性作用。

1 分析流程

基于概率测度的确信可靠性建模与分析方法如图1所示。首先确定产品的关键性能参数与性能阈值。在这一阶段,通常利用功能性能裕量分析(functional performance margin analysis, FPMA)进行确定。基于FPMA的分析结果,利用理论分析、仿真建模、实验建模等方法,构建关键性能参数与设计参数、环境参数、使用参数的函数关系,建立性能方程。结合性能参数阈值,建立裕量方程。

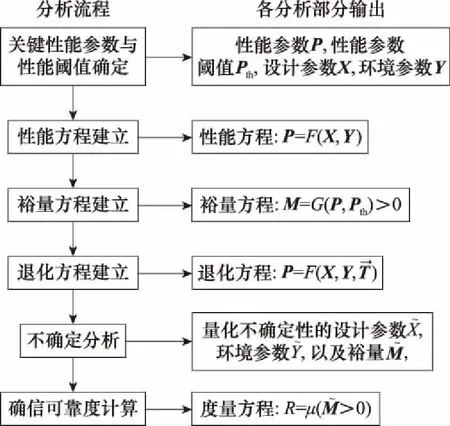
图1 分析流程Fig.1 Analysis process

在退化方程建立阶段,通过开展失效机理分析与退化实验,确定参数的退化规律,结合关键性能参数的裕量方程,建立退化方程。

在不确定分析阶段,通过确定主要参数的分布,量化其不确定性。通过确信可靠度计算从零时刻至任一时刻度量的可靠度,实现产品可靠性的建模与分析。

2 关键性能参数与性能阈值确定

本文利用FPMA确定关键性能参数与性能阈值。FPMA是一种有序开展对产品功能、性能及裕量分析的形式化方法。开展FPMA的根本目的是对产品的功能、性能进行充分理解和分解,获得其主要故障机理、关键性能参数、性能阈值等信息,为后续的可靠性分析、可靠性实验验证等过程奠定基础,为实现产品的预期质量目标提供依据。

FPMA主要包括功能分析、性能分析、阈值分析3部分内容。在功能分析阶段,明确产品基本的结构组成、功能原理、任务剖面等信息,建立对象的结构树、功能树。在性能分析阶段,确定关键性能参数,分析关键性能参数特征,建立研究对象的性能分解表与失效机理分析表,明确可能的影响因素、敏感应力、失效机理等信息。在阈值分析阶段,深化和量化产品需求分析,明确关键性能参数失效的阈值。

一般情况,性能参数阈值有以下几种。

(1) 规范阈值:技术规范中规定的性能参数极限值,可以通过产品规格书或使用手册查询。

(2) 设计阈值:产品设计过程中确定的性能参数设计极限值,通过设计报告或设计手册可以查到这个阈值。

(3) 工作阈值:产品能正常工作的性能参数极限值,可以通过正常条件的性能试验测试确定。

(4) 破坏阈值:产品达到破坏的极限性能参数值,一般通过极限条件下的性能试验确定。

规范阈值、设计阈值、工作阈值和破坏阈值是递增的,在实际分析过程中应依据研究对象的应用场景与工作剖面进行阈值取值。

基于FPMA,明确了研究对象的关键性能参数、性能阈值以及其对应的影响因素、失效机理等信息,为可靠性分析、可靠性实验提供了依据。

3 性能方程建立

由式(1)的裕量方程可知,当阈值确定时,只需要明确性能参数与设计参数、环境参数、使用参数之间的函数关系,建立性能方程,从而量化产品参数的不确定性,计算产品的可靠性。性能方程可采用理论分析、仿真建模与实验建模的方法进行求解。对于全新产品的可靠性设计,由于缺乏样品与实验条件的限制,通常采用仿真建模的方法。仿真建模的步骤如图2所示。

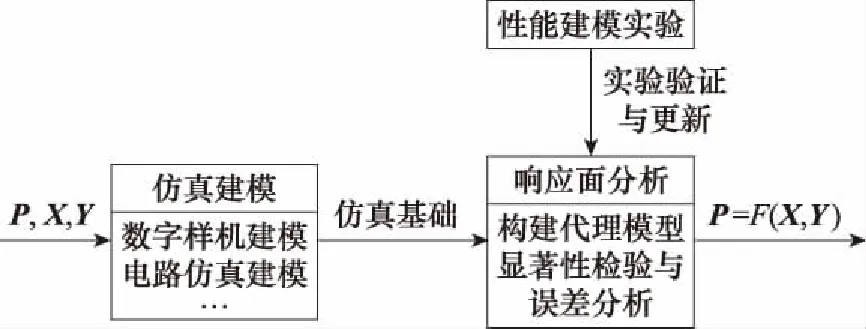
图2 仿真建模步骤Fig.2 Steps of simulation modeling

建立产品的数字样机模型、电路仿真模型等仿真模型,并加载不同的载荷历程,开展仿真分析,从而量化不同工作载荷、环境载荷下关键性能参数的变化,为后续分析提供仿真基础。

完成仿真建模后,对研究对象开展响应面分析,构建关键性能参数的代理模型,拟合关键性能参数与设计参数、环境参数、使用参数之间的函数关系。

响应面分析是一种拟合各因素之间关系的试验设计方法[6]。在响应面分析中,设置特殊的实验或仿真设计,进而拟合得到整体的影响因素与响应之间的函数,并进行优化设计[7]。对于响应面的构造,由于多项式模型具有数学表达式较为简单、计算量小、收敛速度快等特点,并且可以显式表达[8],因此在实际应用中,通常采用多项式近似模型进行分析。

在实际的响应面分析中,基于FPMA分析结果确定影响因素、响应因素以及对应的取值范围,选择合适的响应面设计方法并设置实验,按照实验组因素进行仿真得到响应结果。基于上述流程,便可拟合关键性能参数的代理模型,并对拟合模型进行显著性检验与误差分析来验证模型的准确性。

为了提升性能建模的准确性,可开展性能建模实验作为仿真建模的验证与补充,利用实际实验数据对已有的代理模型进行更新,最终给出更新后的代理模型与性能方程。

在设计实验时,需要确定实验样品的配置以及对应的实验应力与加载方式并设计实验剖面。为了对仿真建模构建的代理模型进行更新,尽量控制实验样品制造与实验剖面设置满足响应面分析中的中心点配置,并将实验响应结果作为响应面分析的中心点结果代入分析,得到更新后的性能参数代理模型。

4 裕量方程建立

对于性能参数的参数特性,可分为以下3类[9]。

(1) 望小特性(smaller-the-better, STB):参数特性值越小越好,特性理想值为0。

(2) 望大特性(larger-the-better, LTB):参数特性值越大越好,特性理想值为无限大。

(3) 望目特性(nominal-the-better, NTB):参数特性具有特定的目标值。

则性能裕量m表示为

(4)

式中:p为性能参数;pth为性能阈值;pth,U为性能阈值的上限值;pth,L为性能阈值的下限值。由裕量方程可知,m≤0时产品失效。

依据关键性能参数的属性确定裕量方程模型,根据FPMA确定的性能阈值与性能方程相结合,建立裕量方程,为后续退化方程建模与确信可靠性分析提供分析基础。

5 退化方程建立

在退化方程建立阶段,通过理论分析与实验分析的方法,针对产品的寿命指标要求,确定关键性能参数全寿命周期内的变化规律,建立关键性能参数的退化方程,为针对寿命指标的确信可靠性分析提供基础。

与性能方程建立过程类似,退化方程的建立可以通过理论分析、仿真建模、实验建模的方法进行。对于理论分析,一般适用于退化机理明确、失效模式单一的对象,不适用于较为复杂的系统以及失效机理尚不明确的研究对象。对于仿真建模,同样需要对研究对象开展耗损型机理分析,在分析的基础上进行数字样机建模,设计并开展仿真应力分析,获取相应应力分析结果作为耗损故障机理的模型输入,拟合模型参数,建立关键性能参数的退化方程。

对于影响因素复杂、难以开展仿真的研究对象,可通过退化实验的方式确定退化方程。依据失效机理分析确定施加应力及水平,计算加速因子,设计退化实验剖面。并开展加速实验,基于实验过程获取应力数据以及产品性能数据,进行确信可靠性退化建模,并对数据进行统计分析,最终建立关键性能参数的退化方程。

6 不确定分析

不确定分析阶段的目的在于确定主要偏差参数与分布形式,通过确定设计参数、环境参数与使用参数的不确定分布来量化参数的不确定性。

在数据样本量充分的情况下,主要考虑固有不确定性的影响,采用概率分布描述参数的不确定性,基于概率统计原理对大样本数据进行统计分析,拟合关注参数的概率分布。在选择参数分布类型时,通常基于以下准则[10]:① 对于已有充分研究的参数,可根据研究结果直接确定分布类型;② 对于未充分研究但存在充分测量样本数据的参数,可通过测量结果进行选择;③ 对于研究不充分且难以测量的参数,可通过先验与专家信息进行假设,在确定参数分布类型后,可基于已有研究与实际检测数据,利用矩估计、最小二乘估计、极大似然估计等参数估计方法计算分布参数。

7 确信可靠度计算

获得参数分布之后,进行关键性能参数的确信可靠度计算。由裕量方程可知,当性能裕量大于0时,可认为产品未发生失效。因此,可靠度可表示为度量方程,即性能裕量大于0的不确定性。将参数分布代入关键性能参数的裕量方程,即可度量性能可靠度。

使用概率测度描述参数不确定性时,可基于随机变量的运算法则计算裕量的概率分布以及可靠度。如果裕量方程形式复杂,难以使用运算法则计算分布,可采用蒙特卡罗方法进行数值仿真,得到性能裕量大于0的概率。针对研究对象的寿命指标,基于关键性能参数的退化方程,将其代入裕量方程,可计算任一时刻的确信可靠度。针对可靠性指标优化产品设计,从而实现可靠性的正向设计与定量设计。

8 案例分析

以某型电连接器为案例,开展确信可靠性建模与分析,验证该可靠性设计流程的可行性。

8.1 关键性能参数与性能阈值确定

针对电连接器开展FPMA,确定其关键性能参数、性能阈值以及可能影响关键性能参数的敏感因素信息、失效机理等。

电连接器主要包括公母胶头、插针插孔、包胶模材料、O型环、内外螺纹、线材等部分,在电气终端之间提供连接与分离功能。

依据产品客户之声(voice of customer, VOC)、DFMEA、结构树、失效分析树、P图等资料,完成了对产品的功能分析。产品主要包括导电(电能量或信号传输)、耐压、绝缘、防水、固定、防呆和插拔7种功能单元。

(1) 导电单元:在端子连接后传输电能量或信号。

(2) 耐压单元:在额定电压内安全运作,以及能够承受振动、插拔以及其他类似现象所引起的瞬间过载。

(3) 绝缘单元:在额定工作电压以及温度、湿度、污染等因素影响下绝缘电阻符合规定要求。

(4) 防水单元:保证使用寿命期间IP67的防护要求。

(5) 固定单元:保证各连接件之间旋转、振动、正常拉拔不松脱,保证防水要求,实现正常的电能量或信号传输。

(6) 防呆单元:避免使用者错误的插拔操作。

(7) 插拔单元:保证连接器良好的操作手感和寿命周期内稳定的插拔力。

在性能分析部分,基于产品VOC以及DFMEA,确定本案例中的关键性能参数为电连接器工作过程中的最大温升。针对温升参数进行性能分解,分析影响温升的结构设计参数,得到性能分解表(见表1),为后续仿真建模提供依据。

表1 电连接器性能分解表

对影响温升的主要单元与失效机理进行分析,得到失效机理分析表(见表2),为退化方程建模提供分析依据。

表2 电连接器失效机理分析表

对于温升,依据行业经验与实验结果,使产品失效的极限性能值,即破坏阈值为30 K。根据GJB/Z 35-1993对于电连接器的降额要求以及产品的实际应用场景,设定产品温升的规范阈值小于破坏阈值25 K,即规范阈值为5 K。后续对于产品温升的确信可靠性分析将基于规范阈值5 K展开。

8.2 性能方程建立

求解温升的性能方程,表征温升与设计参数、环境参数、使用参数的函数关系。首先开展电热仿真,计算不同工作载荷与环境载荷条件下产品的温度变化情况。

研究采用ANSYS Workbench的电热耦合模块进行仿真。对于所需材料参数,根据供应商提供的资料,得到零件、材料与属性如表3所示。

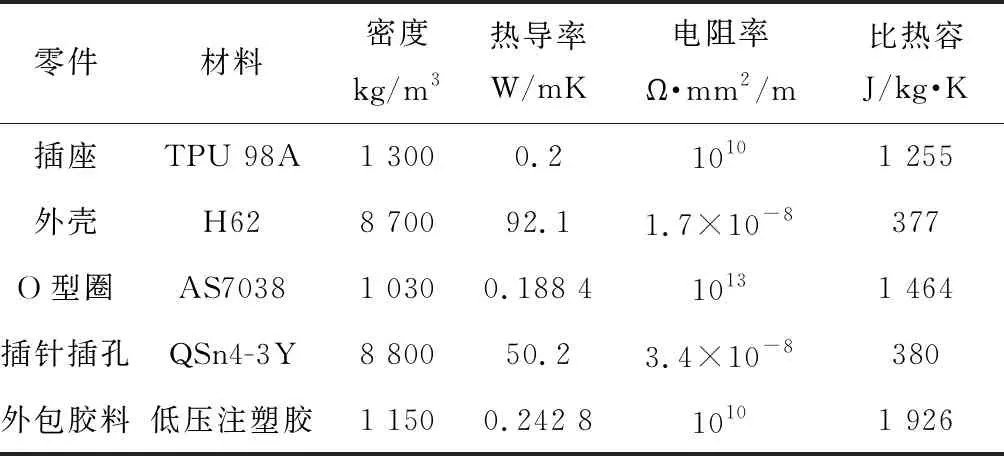
表3 各单元材料及属性

由于开展热仿真分析,探究最大温升,不考虑组件的变形与相对位移,因此各接触对接触类型全部设置为绑定。

根据产品实际约束情况施加约束。环境温度设置为正常工作温度25 ℃。对外壳与外包胶模表面施加对流换热,对流换热系数设置为5.78。对于热辐射,外包胶材料的辐射率按0.95计算,金属外壳表面镀镍,辐射率按0.35计算。

在插针端面施加电载荷,额定电流1 A。在连接器工作过程中,除了导体电阻生热,由于接触表面凹凸不平以及氧化膜、气体吸附层的存在,会产生额外的接触电阻[11]。为了考虑接触电阻的影响,此处将其对温度的影响模拟为在接触件表面时加载功率密度载荷[12]。由产品监测数据可知,正常工作下的接触电阻为4 mΩ左右,由仿真电压监测可知端子电阻为2.164 mΩ,则除体电阻外的接触电阻为1.836 mΩ,插针插孔接触面积经计算为2.865×10-9mm2。计算可得施加的总功率密度为640.81 W/m2。

仿真后产品整体温度状况如图3所示。产品整体最高温度为28.386 ℃,相比环境温度25 ℃上升3.386 ℃。温度最高区域为端子连接处,因此针对电连接器端子部分的温升数据进行分析并以此进行建模。在仿真模型的基础上,进行响应面优化,计算温升的代理模型,拟合温升与设计参数、环境参数以及使用参数的函数关系。

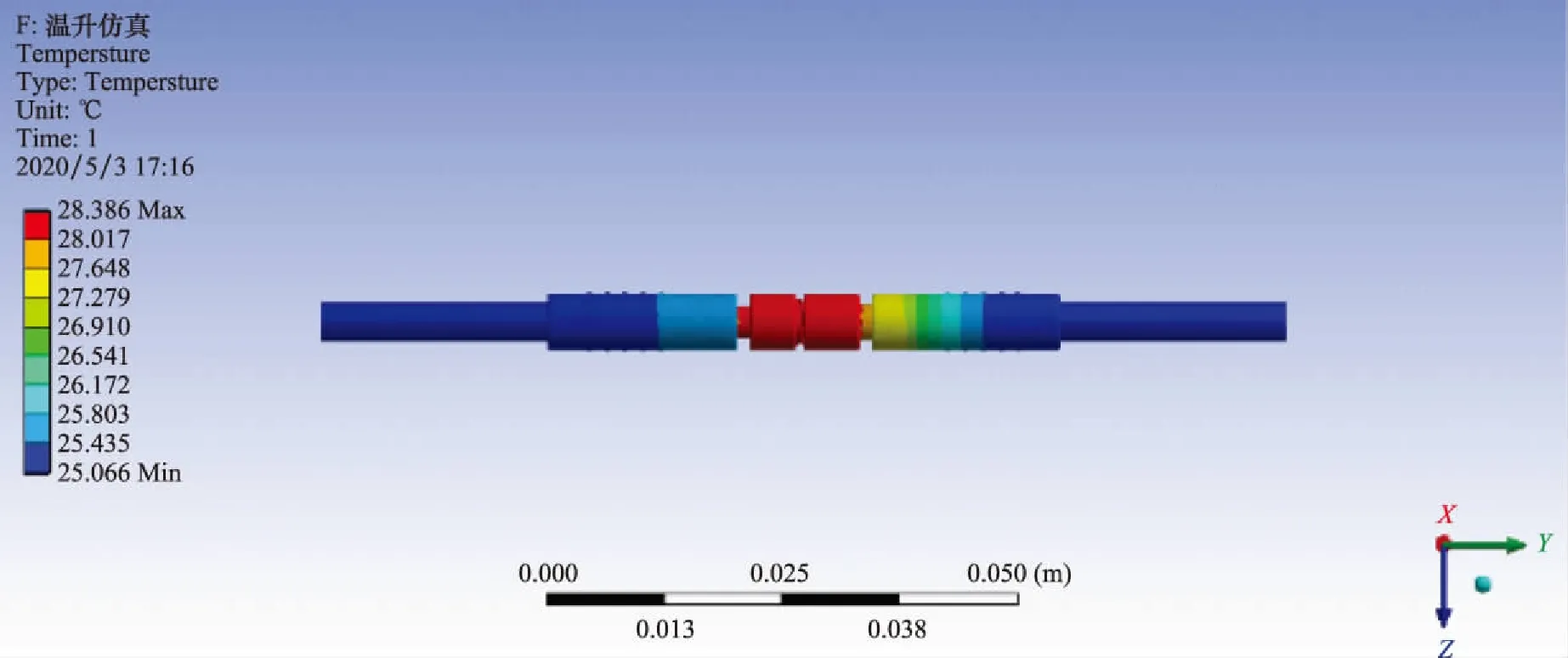
图3 25 ℃环境下产品温度分布Fig.3 Product temperature distribution under 25 ℃ environment

根据已完成的FPMA,影响温升的设计参数为导体电阻率以及表征端子横截面积的端子半径。研究表明,电镀规格与插孔分离力主要影响体电阻外的接触电阻[13],因此将接触电阻作为影响温升的参数。对于环境参数则考虑环境温度对温升的影响。对于使用参数则考虑电流的影响。响应因素即为温升。对于因素范围的确定,需要保证所取值位于可行域中,能保证实验以及仿真能正常实现,不会由于载荷过大等原因导致产品破坏或仿真中断,所取范围如表4所示。

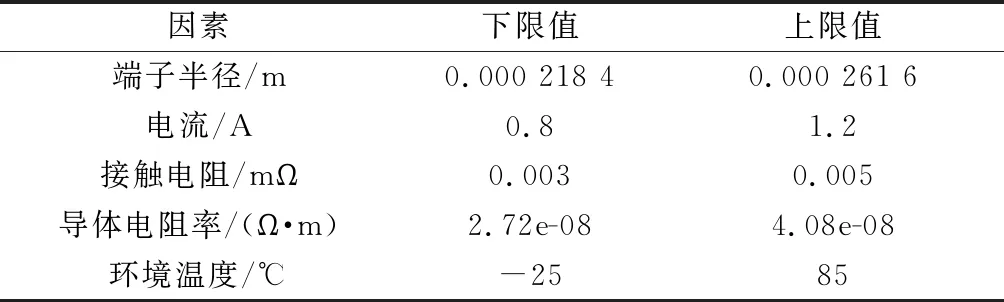
表4 响应面分析因素

采用Box-Behnken Design (BBD)方法,利用Design-Expert软件设计试验,并利用ANSYS Workbench按照试验设定因素进行仿真。

经过显著性检验,本次研究采用二阶模型拟合代理模型,得到拟合函数:

ΔT=6.667 19-41 294.916 63D1-4.481 53I-

586.140 03R+1.605 87×107ρ+0.017T-

20 949.074 07D1I-7.638 89×105D1R-2.433 96×

1011D1ρ+24.200 34D1T+1 636.25IR+

1.058 82×108Iρ-0.018 409IT-1.176 47×109Rρ-

2.168 18RT-1.530 75×105ρT+1.294 77×

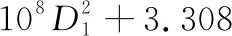
(5)

式中:ΔT指温升;D1指端子半径;I指电流;R指接触电阻;ρ指端子电阻率;T指环境温度。对模型进行显著性检验与相关性检验,计算得到模型F值为7 703.75,表示该模型符合假设。

对拟合出的回归方程进行误差统计分析,多元相关系数R2为0.999 9,说明具有强相关性;变异系数C.V.%=0.515 9%<10%,表明实验的可信度和精确度较高;有效信噪比计算结果为343.962 76,大于4则视为合理[14]。可以看到,拟合的方程符合上述检验性原则,证明其具有良好的适应性。

在性能建模实验阶段,为了验证代理模型,选取电连接器端子样品进行温升测试实验,检测其接触电阻等参数以及最大温升,验证并更新温升代理模型结果,如图4所示。依据GB/T 5095.3—19975a,选取5个插针插孔接触对,进行温升测试实验,记录温度随时间变化曲线。环境温度设置为25 ℃,电流为1 A,通电时间为4 h,如图5所示。各接触对的接触电阻以及最大温升如表5所示,其中S5温升显著高于其他实验组,分析是由于焊接不良造成实验数据异常,因此在后处理中剔除该组数据。

图4 实验前端子接线情况Fig.4 Terminal wiring before experiment environment

图5 端子放置于隔热箱中进行实验Fig.5 Terminals placed in the heat insulation box for experiment

由温升测试数据可知,端子工作过程中的最大温升与仿真结果相差较小,平均误差为11.26%,证明温升的仿真建模能够较好地拟合实际情况。将S1～S44组数据加入响应面分析中,经过显著性检验,最终得到温升的代理模型为

ΔT=6.508 72-41 431.391 71D1-4.488 16I-

588.975R+1.605 87×107ρ+0.016 99T-

20 949.074 07D1I-7.638 89×105D1R-2.433 96×

1011D1ρ+24.200 34D1T+1 636.25IR+

1.058 82×108Iρ-0.018 409IT-1.176 47×

109Rρ-2.166 29RT-1.530 75×105ρT+

2.465 43×10-6T2

(6)

表5 端子接触电阻、最大温升、仿真温升与相对误差

对上述模型进行误差统计分析,相关系数R2为0.998 6,变异系数C.V.%为1.57%,有效信噪比为116.096。更新之后的温升代理模型适应性好,可以很好地拟合实际温升情况。

对更新前后代理模型进行误差验证,结果如表6所示。更新前代理模型平均误差为20.07%,更新后代理模型平均误差为14.45%,模型更新更有良好的效果。对响应分析模型进行求解。采用软件进行优化,设置响应值最小值。此时设置环境温度固定为25℃,得到优化结果如图6所示。

表6 更新前后模型相对误差

图6 温升响应面分析优化结果Fig.6 Temperature rise response surface analysis optimization results

为使温升尽可能小,接触电阻、电流都取误差范围内的最小值,导体电阻率取3.8E-08。而表征端子横截面积的端子半径则取0.000 246 019 m。此即为通过响应面分析得到对于端子半径这一产品设计参数的理论优化结果。

8.3 裕量方程建立

经过仿真建模与响应面分析以及性能建模实验的验证与更新,最终得到温升的性能方程。结合温升阈值,建立温升的裕量方程：

MΔT=ΔTm-ΔT=

5-(6.508 72-41 431.391 71D1-4.488 16I-

588.975R+1.605 87×107ρ+0.016 99T-

20 949.074 07D1I-7.638 89×105D1R-

2.433 96×1011D1ρ+24.200 34D1T+

1 636.25IR+1.058 82×108Iρ-0.018 409IT-

1.176 47×109Rρ-2.166 29RT-1.530 75×

9 220.050 13R2+2.465 43×10-6T2)>0

(7)

式中:MΔT为温升的性能裕量;ΔTm为温升规范阈值;ΔT指温升;D1为端子半径;I为电流;R为接触电阻;ρ为端子材料电阻率;T为环境温度。

8.4 退化方程建立

对于电连接器的各设计因素,插针插孔接触对的接触电阻会在产品实际使用过程中发生退化,由出厂时的低值逐渐变大,进而导致温升上升,最终致使产品失效。

在插拔初期,接触表面的接触点会随着插拔的推碾发生塑性变形,使实际的接触面积增加,收缩电阻减小[15],而膜层电阻也会由于氧化膜层的磨损而减小。随着插拔次数的增加,表面摩擦产生的磨屑会使得镀金层严重磨损,甚至裸露基体铜,接触表面质量严重下降,收缩电阻逐渐增大。而由于基体铜的裸露以及表面质量下降,表面氧化加剧,膜层电阻也会逐渐增加[16]。同时经过多次插拔,端子本身也会发生形变,从而导致正压力下降,接触电阻增加[17]。因此研究表明,接触电阻随插拔次数呈现波动中增加的趋势,且初期波动较大,波动幅度会随插拔次数逐渐减小。

研究采用实验的方式确定接触电阻的退化规律。研究对象的质量目标为插拔寿命100次,设计退化实验为机械插拔寿命实验,利用实验过程中监测的接触电阻值,度量插拔次数对于接触电阻的影响,拟合接触电阻与插拔次数的函数关系。

参照GB/T 5095.5-1997、IEC 61076-2-105-2008(M5)、SAE/USCAR 2标准,选取5个插针插孔接触对,进行机械插拔实验,试验时操作速率为8～10次/min。端子在无电负荷的情况下,经过500次的机械插拔。每隔50次插拔,测量接触对的接触电阻并记录。

实验之后5个插针插孔接触对接触电阻以及平均接触电阻随插拔次数变化情况如表7所示,数据折线图如图7和图8所示。

图7 5个插针插孔接触对接触电阻变化Fig.7 Change of contact resistance of five pairs of terminals

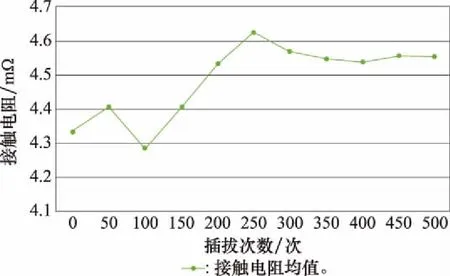
图8 平均接触电阻变化Fig.8 Average contact resistance change

表7 接触电阻随插拔次数变化情况

基于失效机理分析以及实际实验结果,对于接触电阻随插拔次数变化的趋势采用线性函数与结合指数因子的三角函数加和的函数形式来拟合,具体为

(8)

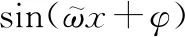
表8 退化曲线拟合结果

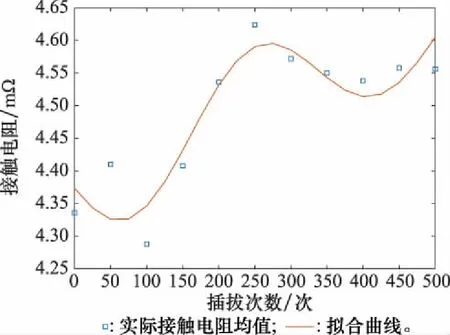
图9 拟合曲线与实际接触电阻均值分布Fig.9 Fitting curve and actual mean value distribution of contact resistance

经计算,拟合曲线各点误差绝对值的期望为0.729 961 603%。由R2、拟合图像以及相对误差可以看出在数据较少的情况下,当前结果能够较好地拟合变化趋势且不过拟合。综上,接触电阻随插拔次数的退化方程为

R=0.000 474 7t+4.388+

0.104e-0.000 850 4tsin(29.89t+18.71)

(9)

式中:R为接触电阻;t为插拔次数。

8.5 不确定分析

为量化各参数的不确定性,研究选取100个样品进行产品端子半径以及接触电阻的检测。由于数据量比较大,因此本次研究假设这两个参数为随机变量,遵循正态分布,并采用极大似然估计拟合正态分布的均值与方差。对于电流偏差与端子材料误差引起的电阻率偏差,同样假设其遵循正态分布[18],并设置变异系数为0.1与0.05。

8.6 确信可靠度计算

8.6.1 固有可靠度计算

基于度量方程与计算得到的裕量方程,采用蒙特卡罗方法进行随机抽样,利用数值仿真求解裕量大于0的概率。将如表9所示的参数分布数据代入,计算在不同环境温度下的产品确信可靠度,环境温度取-25 ℃、30 ℃、85 ℃。温升规范阈值为5 K,数值仿真得到可靠度结果如表10所示。

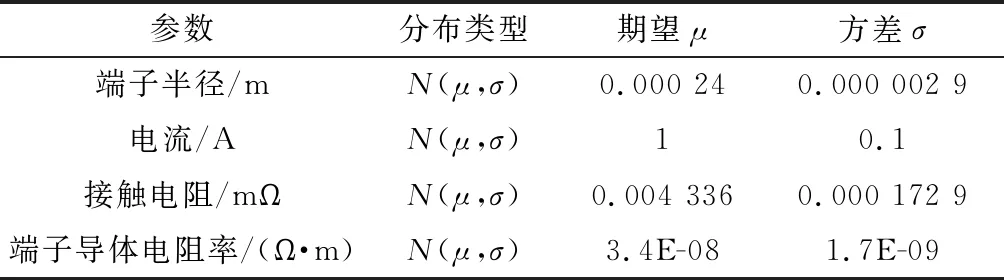
表9 参数分布

表10 不同环境温度下的固有可靠度

各环境温度下产品温升固有可靠度较高。这说明当前对于各参数设计合理,对于端子半径、接触电阻的不确定性控制到位,产品在出厂时可以保证较高的可靠度。下面基于数值仿真结果进行参数敏感度的分析。

(1) 端子半径

如图10所示,温升可靠度随端子半径的均值变化比较明显,而端子半径方差对于可靠度的影响较小。端子半径的均值在0.2～0.25 mm时可靠度呈线性增长趋势,在0.25～0.3 mm范围内可靠度曲面逐渐平缓。而可靠度随半径方差的变化不明显,曲面平缓。

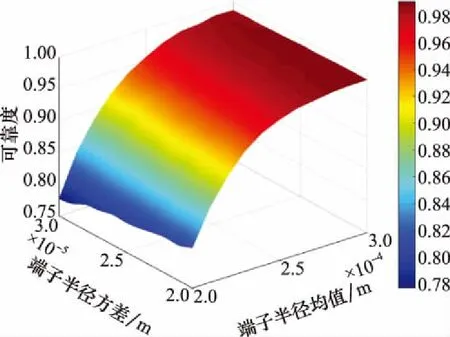
图10 温升可靠度随端子半径均值与方差变化Fig.10 Temperature rise reliability varies with terminal radius mean and variance

(2) 电流

而对于电流,其均值与方差变化对温升可靠度影响均比较明显。在电流均值较小时,可靠度接近1;而电流均值较大时,可靠度下降明显。在均值较小时,方差越小可靠度越高;在均值较大时,方差越大反而可靠度越高(见图11)。

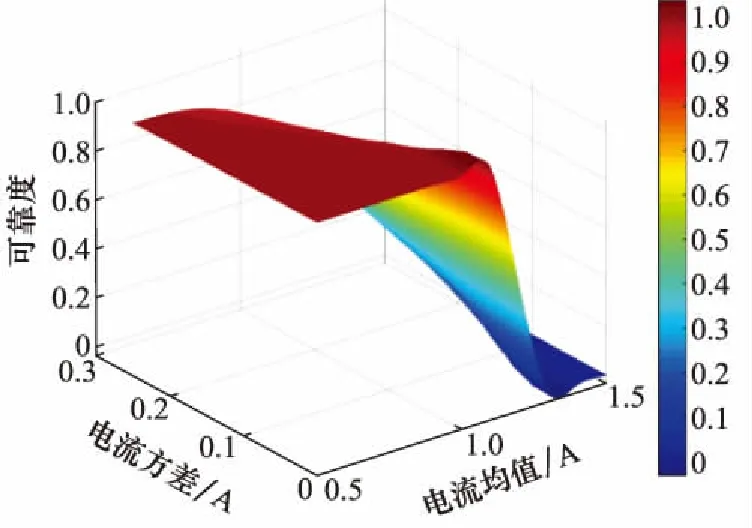
图11 温升可靠度随电流均值与方差变化Fig.11 Temperature rise reliability varies with current mean and variance

在电流均值较小时,方差越小可以保证不会出现过大的奇异值,而在电流均值较大时,较大的方差会导致出现真实值进而提高可靠度。这对于望小特性的参数是通用的。

(3) 接触电阻

如图12所示,接触电阻的均值对产品可靠度影响明显。可靠度随接触电阻均值增加而下降。在接触电阻较小时,可靠度接近1;而接触电阻较大(如大于4 mΩ)时,产品可靠度下降明显。可靠度随接触电阻方差也存在类似上述电流方差变化的趋势,但变化不明显,趋势平缓。

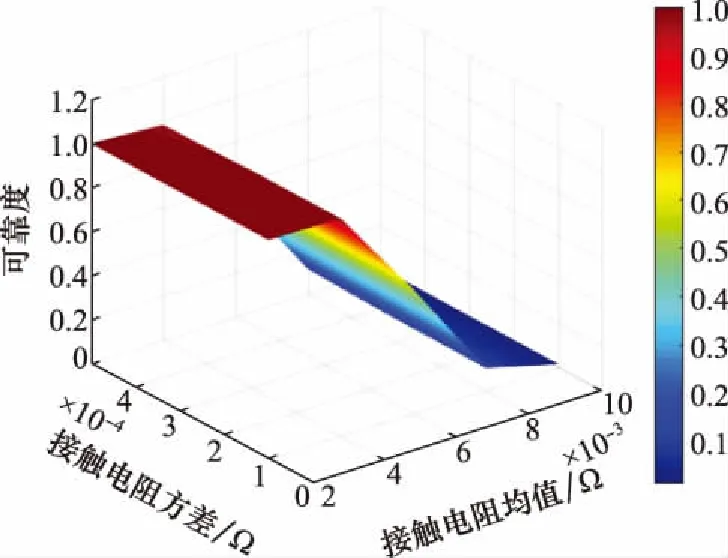
图12 温升可靠度随接触电阻均值与方差变化Fig.12 Temperature rise reliability varies with the mean and variance of contact resistance

(4) 导体电阻率

如图13所示,可靠度随导体电阻率均值的增加整体下降,而电阻率方差对于产品可靠性影响不大。由于在产品材料确定的情况下导体电阻率偏差较小,且几乎不发生退化,因此导体电阻率对于可靠度的影响较小。

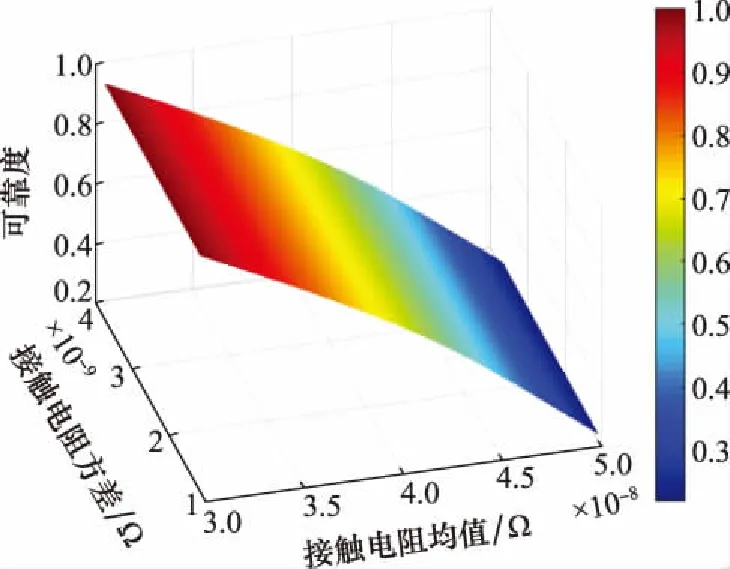
图13 温升可靠度随导体电阻率均值与方差变化Fig.13 Temperature rise reliability varies with the mean and variance of conductor resistivity

(5) 环境温度

图14为环境温度变化对于可靠度的影响。随着环境温度上升,产品可靠度呈增长趋势。研究表明[19],环境温度升高加快了产品热传导、热对流、热辐射的速率,辐射系数增大,散热系数增大,有利于产品与环境的热交换,从而导致产品相比于环境温度的温升有所降低,进而提升了温升参数的可靠度。由于绝对温度的升高可能会引发其他可靠性、安全性相关的问题,后续研究可以以绝对温度作为关键性能参数评价和优化产品。通过对各因素均值与方差的分析,可知连接器的端子半径均值、电流均值与方差、接触电阻均值对可靠度影响较大。

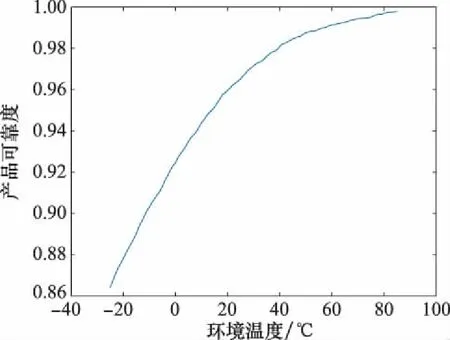
图14 环境温度对于温升可靠度的影响Fig.14 Influence of ambient temperature on temperature rise reliability

对于端子半径,需要在满足其他条件的情况下,优化半径设计,以及在生产过程中进行严格的质量管理。对于电流因素,应注重降额设计,并且确保产品工作环境的电应力稳定。对于接触电阻,一方面应控制端子电阻率偏差,严格端子材料的质量把控,减少材料杂质,降低残次品率;另一方面在生产过程中严格把关端子表面的电镀规格以减缓镀层的氧化腐蚀,以及严格插针插孔尺寸以及缩口处理,以确保插孔分离力不致使插针插孔松脱。

8.6.2 使用可靠度计算

由退化方程建立得到接触电阻随插拔次数的退化方程。将实验检测数据与模型拟合数据进行数值仿真得到产品可靠度随插拔次数变化的趋势。由计算结果可知,随着接触电阻在插拔过程中的波动,温升可靠度也产生波动并且呈现整体下降的趋势。为了保证产品的使用可靠性,需要在产品设计阶段增大温升裕量,延缓接触电阻退化,控制各设计参数、环境参数与使用参数的不确定性。