基于模态分析的印刷电路板力学性能研究
2021-07-05周嘉诚毛宽民
胡 超 ,刘 芳 ,周嘉诚 ,毛宽民
(1.宁夏大学 机械工程学院,宁夏 银川 750021;2.武汉纺织大学 机械工程与自动化学院,湖北 武汉 430073;3.华中科技大学 机械科学与工程学院,湖北武汉 430074)
伴随中国智能制造2025 的不断推进,电子科技技术飞速发展,人们对于电子设备可靠性的需求也越来越高,电子设备尺寸、形态等也在不断地更新迭代。电路板作为电子设备的核心部件,特别是在无人机狭小舱内、高温车载等复杂工况振动环境下,采用四周固定约束方式,其结构的稳定性与抗冲击能力一直备受学者们关注。据研究表明,振动对印刷电路板及其组件系统的性能和稳定性有着非常大的影响[1-2]。因此,对印制电路板(PCB 板)及元器件进行模态分析和振动特性分析是非常重要的。
周嘉诚等[3]利用ANSYS 有限元软件对无人机用PCB 板进行模态仿真分析,通过改变PCB 板的芯片布局及增加紧固点的方式加强了PCB 板的抗振能力,提高了PCB 板的稳定性。李本等[4]利用ANSYS 软件,对某火控PCB 板进行了一系列动力学特性分析,找到了该PCB 板的共振点及易损点的位置,同时利用试验模态分析验证了该模型的准确性。王文博[5]利用ANSYS APDL 对机载PCB 板进行建模仿真,提出转换约束安装方式,采用预应力安装及板面增加加强筋的方法,实现PCB 板的抗振优化。鲍丙豪等[6]利用ABAQUS 软件对印刷电路板组件(PCBA)进行了模态仿真及试验模态分析,发现固定方式及芯片分布位置对PCB 板的可靠性影响较大。
虽然在电路板结构分布、焊点可靠性和约束方式上已有诸多解决方法,但是多为理论分析判断电路板易损位置,对电路板及组件在军用试验条件下的力学可靠性研究较少,并没有依据相关标准试验来检验判断。本文根据某电子产品的印刷电路板,设计改进了其结构及元器件分布,利用有限元仿真软件ANSYS Workbench 对印刷电路板进行建模及模态分析。同时,采用锤击模态试验法,测试了该印刷电路板的频率及振型,通过与仿真结果相对比,确保了印刷电路板建模的准确性。然后依据军用试验指标,对该有限元模型进行了频率响应分析及随机振动分析,并与模态结果进行了对比。
1 模型建立
所设计的印刷电路板长132 mm,宽77 mm,厚1 mm,3 排5 列共15 个芯片接口,9 块边长为5.5 mm 的芯片通过无铅焊点焊接在印刷电路板上,印制电路板模型如图1 所示。

图1 印制电路板模型Fig.1 Printed circuit board model
印制电路板、芯片以及无铅焊点的材料参数如表1 所示。
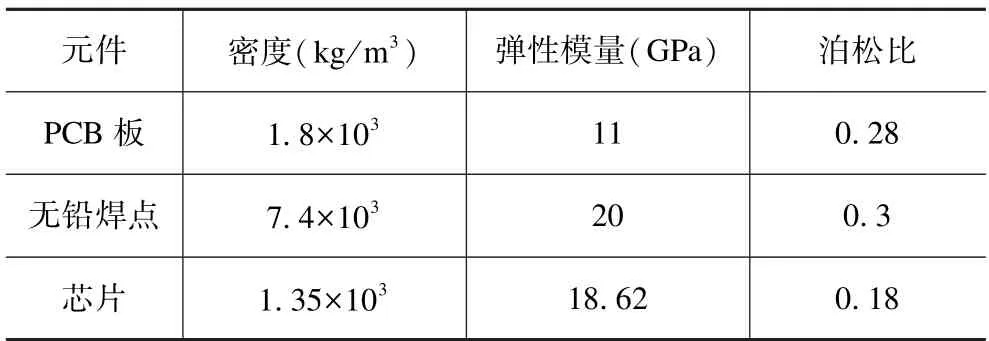
表1 印制电路板材料参数Tab.1 Printed circuit board material parameters
本文建立有限元模型采用的是ANSYS Workbench软件平台,与经典的ANSYS APDL 相比,求解模块相同,但Workbench 具有操作简易、模块化程度较高等优点。同时,在建立有限元模型时,考虑到有限元软件计算时间及效率问题,特将焊点简化成6 mm 的正方形薄片。有限元模型如图2 所示,利用Multizone 方法定义Hexa 类型对该模型进行网格划分,模型包含有193918 个单元,78900 个节点,单元为Solid 186 模型。该单元为具有大变形、大应变以及蠕变等特性的正六面体单元,含有20 个节点数,每个节点都具有x、y、z三个方向的平移自由度。印刷电路板、无铅焊点及芯片之间采用Boned 的约束连接关系,即经典APDL模式下的MPC 约束算法。引脚及部分结构采用了简化处理。

图2 有限元模型Fig.2 Finite element model
2 模态试验及仿真分析
2.1 模态试验
采用四周固定的方式将印刷电路板用螺栓固定在自制的夹具稳定台上,利用西门子LMS 振动测试平台进行锤击模态测试,测试现场如图3 所示。

图3 模态试验现场Fig.3 Modal test site
选用的传感器为东华测试的微小型IEPE 压电式加速度传感器,力锤为PCB 公司的微型力锤。试验前,在LMS 模态分析模块内对印刷电路板模型进行建模,选取9 个响应点并建立其对应的坐标,定义其中一个点为激励点,通过点对点的连线来描述实体尺寸结构。同时,考虑到电路板尺寸问题,试验采取单输入单输出的形式,即锤击同一个激励点,每次锤击采样前更换加速度传感器贴放位置(更换到下一个响应点)。将输入的力信号与响应信号采集后,通过LMS 模态分析模块进行数据分析,得到的前四阶模态试验结果分别如图4(a)、(b)、(c)和(d)所示,固有频率如表2 所示。白色连线平面及固定序号点1~3 为原始模型,离开白色平面的凹凸点连线及序号点1′~3′为模态试验振型,序号点1~3 与序号点1′~3′一一对应。
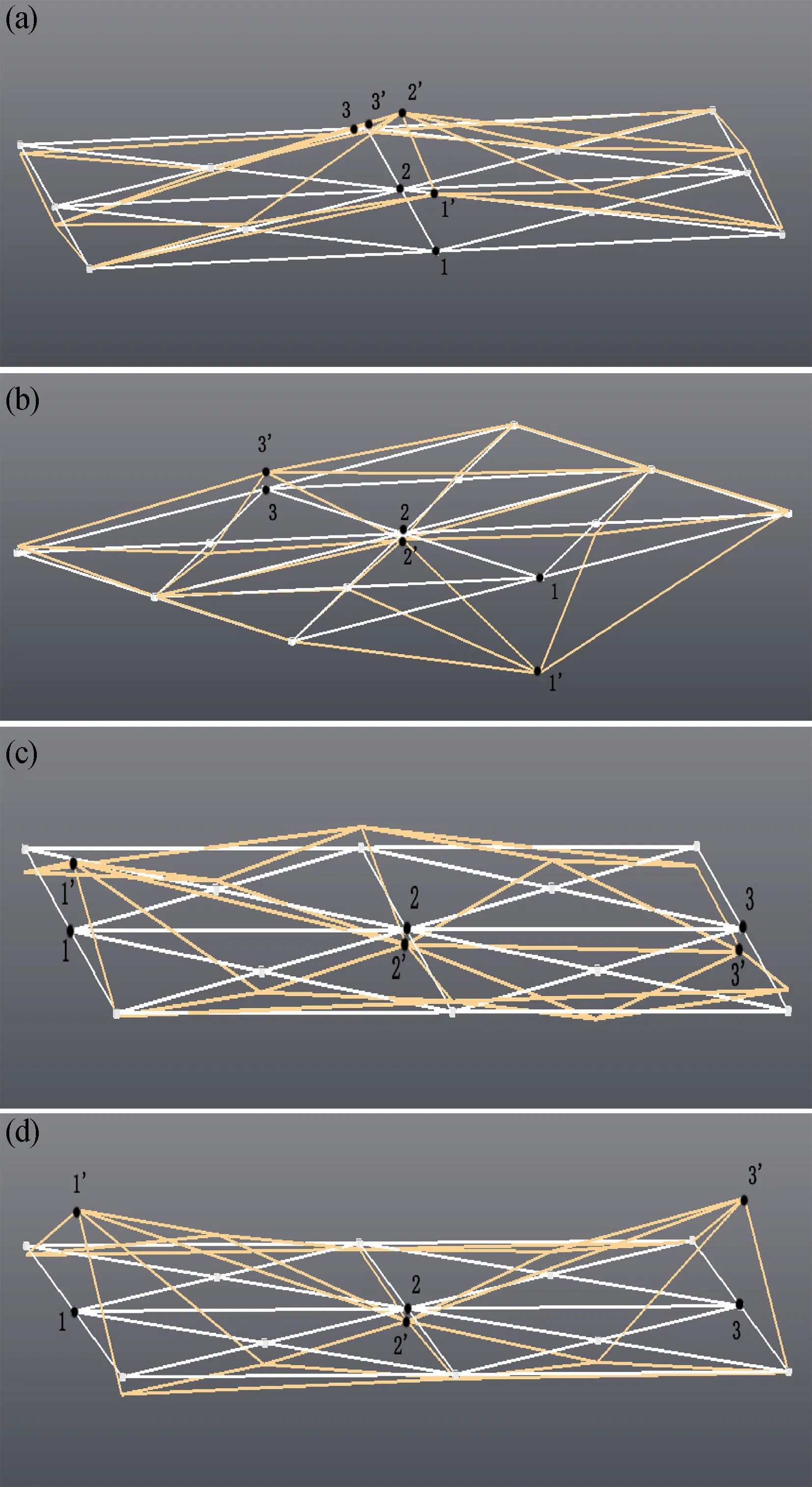
图4 (a)模态试验一阶振型;(b)模态试验二阶振型;(c)模态试验三阶振型;(d)模态试验四阶振型Fig.4 (a)Mode test first-order mode;(b)Mode test second-order mode;(c)Mode test third-order mode;(d)Mode test fourth-order mode
2.2 模态仿真
采用Workbench Modal 模块对印刷电路板进行模态仿真分析。为更好地与实际模态测试环境约束相对应,使用Fixed Support 约束螺栓孔,忽略螺栓预紧力作用。Solver Type 选择为Direct(直接法),即经典APDL 下的Block Lanczos 法。求解得出该系统前五阶模态的固有频率,如表2 所示。前四阶固有模态振型依次见图5(a)、(b)、(c)和(d)。
由图5 和表2 可知,印刷电路板在四角固定约束的情况下,仿真计算求解出的一阶固有频率为275.58 Hz,振型为弯曲形变,最大变形发生在无约束的中线部位,容易造成芯片及焊点的疲劳破坏。越靠近两边约束位置,PCB 板的变形量越小,这说明四周固定的约束方式不会造成固定处的螺栓紧固件产生较大的局部应力。后三阶模态的振型多为翘曲,局部变形量较大,约束位置同样变形量较小,可在出现局部变形处添加约束,防止较大变形损坏电路板。三阶与四阶模态固有频率相近,振型区别不大。仿真结果与试验模态的各阶频率差值都在5%以内,振型吻合度较高,说明该印制电路板的有限元建模方法有较好的准确性。同时,确定了其一阶固有频率,通过调频等手段可避免工况频率接近固有频率时产生共振现象[7]。
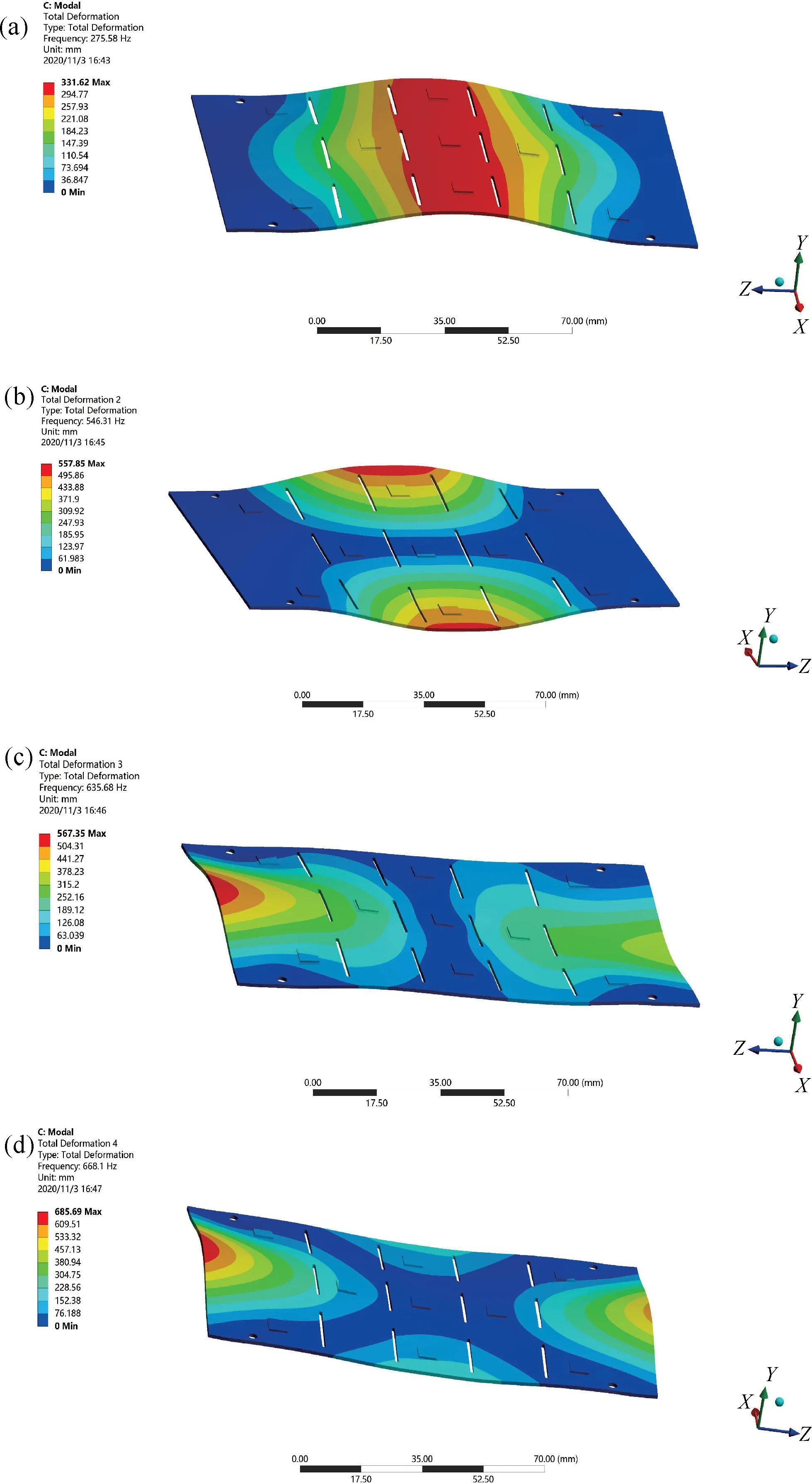
图5 (a)模态分析一阶振型;(b)模态分析二阶振型;(c)模态分析三阶振型;(d)模态分析四阶振型Fig.5 (a)Modal analysis first-order mode;(b)Modal analysis second-order mode;(c)Modal analysis third-order mode;(d)Modal analysis fourth-order mode
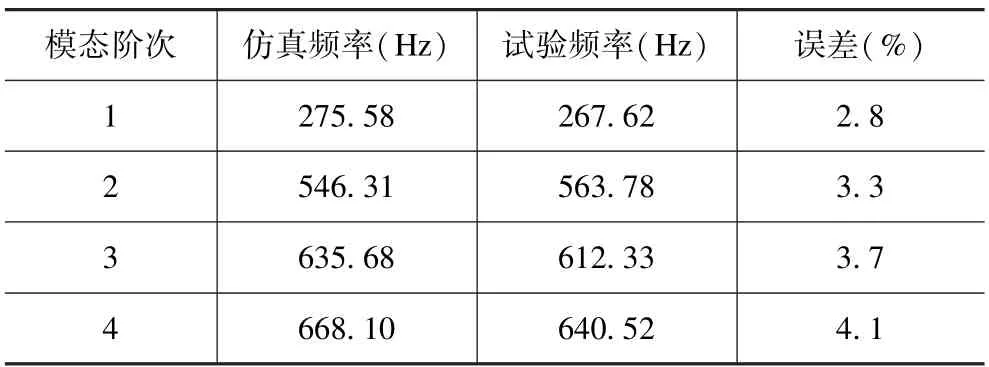
表2 模态仿真及试验对比Tab.2 Modal simulation and test comparison
3 冲击响应及随机振动分析
3.1 冲击响应分析
冲击是电子设备所受外界最普遍的影响之一,剧烈的瞬时运动会使系统加速度、速度、应力及位移等发生显著突变,对PCB 板造成永久性损坏[8]。工况下的冲击激励往往是十分复杂的,为模拟冲击激励,可以将其处理成具有一定规则性的响应谱形式,比如矩形、后峰锯齿形等。本文参照国军标GJB150.18-86 军用设备环境试验方法的冲击试验[9],采用半正弦波对PCB 板进行冲击响应分析,其表达式如式(1):
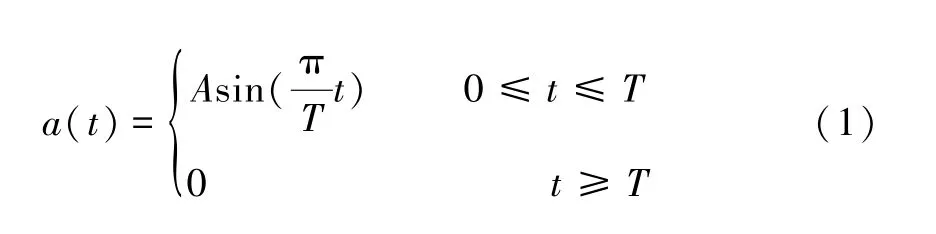
式中:A为加速度幅值;T为冲击时间。
采用Workbench 中的Transient Structural 模块进行冲击响应分析,在该PCB 板有限元模型的约束处定义半正弦波的加速度载荷,加速度峰值为50g,冲击时间为11 ms,选择模态叠加法,采用时间增量步进行有限差分计算,得到瞬时下y方向上的加速度及位移响应分别如图6 和图7 所示。
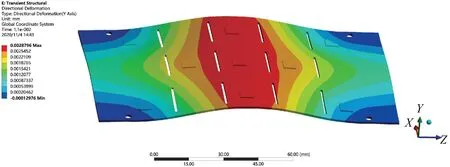
图6 y 方向上的位移响应图Fig.6 Displacement response diagram in y direction
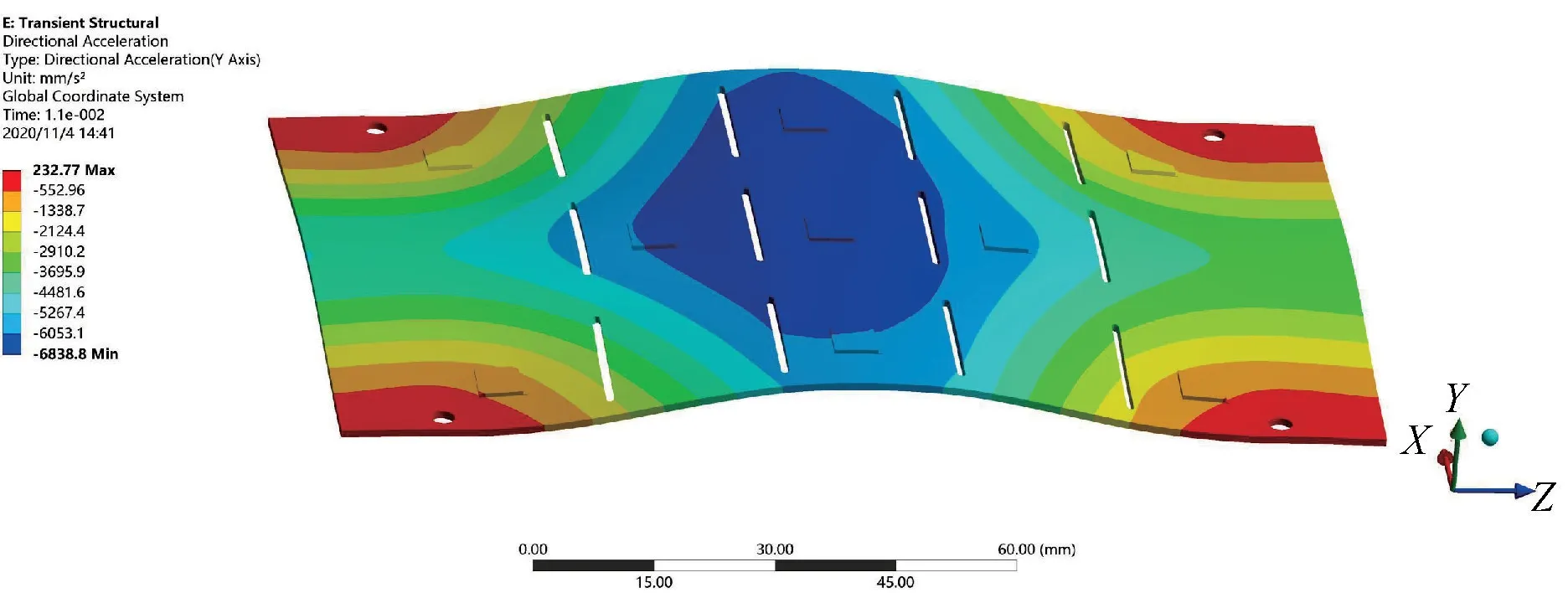
图7 y 方向上的加速度响应图Fig.7 Acceleration response diagram in y direction
由上述应力云图可以看出,受到瞬态冲击后,位移响应主要发生在PCB 板的中线部位,此时弯曲变形量最大,最大位移量为0.00254 mm,与模态一阶振型相符。冲击响应向约束部位处逐渐减缓,说明四周固定约束对PCB 板的抗冲击能力有着一定作用。中线部位加速度响应的绝对值最大,响应较为剧烈,会对中线部位的芯片及焊点造成影响,需要做一定的加固处理。中线处与四角处加速度方向相反,印刷电路板的耐受能力和强度需要达到一定的程度。
3.2 随机振动分析
电子设备大约有30%以上的失效或者故障是由于振动引发的,尤其是宽频随机振动。工况下的随机振动如果超过设计极限值,将会引起焊点破坏,影响PCB 板的稳定性及可靠性[10-11]。采用Workbench 中的Random Vibration 模块进行随机振动分析,PCB 板约束情况与模态分析相一致,载荷谱采用国军标GJB150-86 环境试验要求中典型的宽带加速度功率谱密度[10],频率范围为20~2000 Hz,如图8 所示。
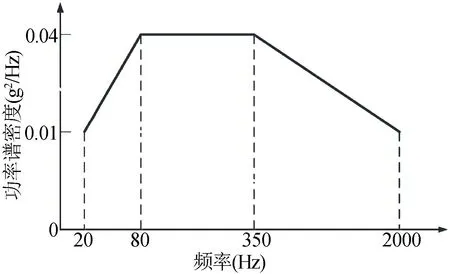
图8 典型随机振动加速度激励谱Fig.8 Typical random vibration acceleration excitation spectrum
在随机振动分析输出的响应值中,1σ解采用Steinberg 的高斯分布三区间法,假定所有参数都是服从平均值为0 的(高斯)正态分布,即响应值服从标准差为σ的正态分布[12-13]。1σ下电路板的应力响应分布如图9 所示,1σ下焊点部位的应力响应分布如图10所示。
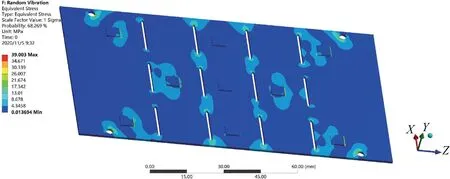
图9 1σ 下电路板的应力响应图Fig.9 Stress response graph of circuit board under 1σ
根据随机振动的理论,计算一阶响应公式为:
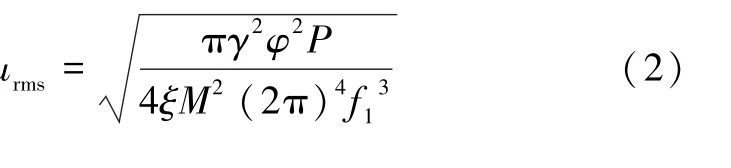
式中:urms为1σ下单方向上的位移响应;ξ为阻尼比;f1为一阶固有频率;M为广义质量;γ为模态参与系数;φ为一阶模态振型;P为加速度形式输入参数。
由上述仿真结果可知,一阶模态1σ下单方向响应为0.085 mm,参考一阶模态仿真最大应变值计算随机振动响应理论值为0.078 mm,二者结果接近,说明此随机振动仿真合理。从上述应力云图可以看出:约束处的最大应力响应值为17.342 MPa,芯片处的应力响应较小,没有产生局部应力。局部应力响应主要集中在焊点处,如图10 中局部放大图所示,此时的最大局部应力为39.003 MPa,位于左上焊点处,靠近约束处的焊点需要额外的加强。
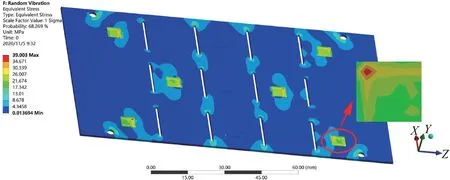
图10 1σ 下焊点的应力响应图Fig.10 Stress response diagram of solder joint under 1σ
此外,y方向上的位移响应如图11 所示,由图11可以看出,最大变形量为0.3214 mm,变形量从中线向两端缓减,这与模态分析得到的振型相吻合,中线处的位移量较大,会对印刷电路板在工况下的稳定性造成一定影响。
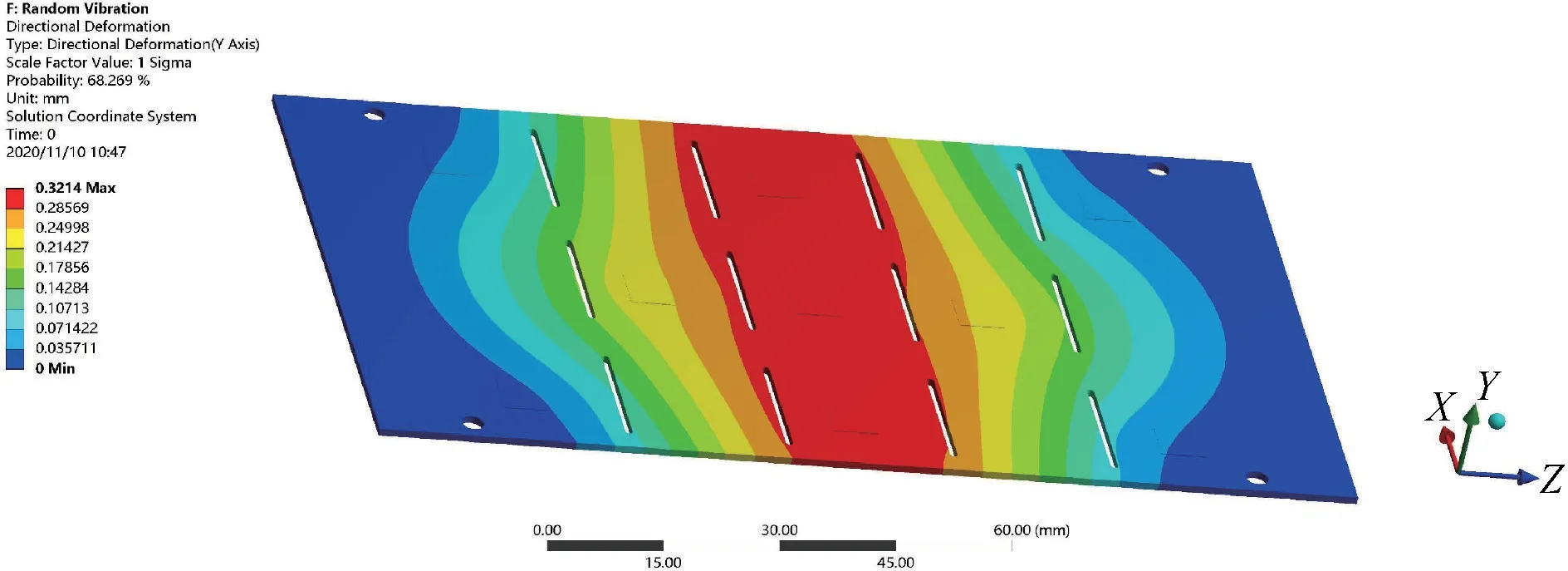
图11 y 方向上的位移响应图Fig.11 Displacement response diagram in y direction
4 结论
(1)本文利用ANSYS Workbench 对某印刷电路板进行了有限元建模,通过模态仿真和模态试验相对比,验证了该建模方法及所建立的PCB 板模型的准确性和实用性。
(2)通过模态仿真及模态试验分析,获得了该PCB 板的动力学特性,其一阶固有频率为275.58 Hz,振型为PCB 板中线附近发生弯曲形变,说明中线部位的芯片容易损坏。为后续PCB 板的抗振优化设计、避免共振等问题提供了基础。
(3)依据军用技术标准的电子设备试验环境对该PCB 板进行了冲击响应及随机振动分析。发现在典型的激励下,该电路板的应力应变指标都在许用范围内。但也存在着局部应力较大、中线处造成芯片及焊点损坏等问题。为后续该PCB 板的结构优化及可靠性分析提供了一定指导依据。
(4)冲击响应与随机振动求解得到的位移响应与模态分析相符,预测最易失效的芯片位置一致,都位于中线处,可以进行有选择性的仿真。
