单热源热流陀螺仪敏感机理的研究
2021-07-05朴林华王育新
李 备,朴林华,王育新
(北京信息科技大学 理学院,北京 100192)
传统的微机械陀螺仪都是利用固体质量块来检测加速度或角速度,这种结构会导致陀螺仪出现诸多问题,如抗冲击能力差、体积无法进一步缩小、难以集成、性能不稳定、灵敏度不高等。近年来,利用热流代替固体质量检测加速度或角速度的微型热流体陀螺仪可解决这些问题。Zhu 等[1]提出了一种新型微机械角速度传感器,该传感器是基于中央加热器的自然对流传热工作的,可将角速度的变化转换为气流方向的偏移,进而引起温度场的变化,通过检测温度的变化量敏感角速度。该传感器可作为角速度传感器,也可作为双轴加速度计。后来,Leung 等[2]通过体硅加工技术制作了热对流加速度计,这种加速度计频率响应好、成本低,极具市场潜力。然而,这些热对流陀螺仪或加速度计通常需要大体积的微机械腔体,无法进一步小型化,在进一步加热的过程中无法产生明显的温度差,造成其角速度信号不易检测、灵敏度太低。大多数热对流陀螺仪或加速度计使用较长的加热丝加热周围环境,需要消耗大量的功率,导致其无法应用于便携式电子设备[3]。因此研究一种低功耗、体积小、高灵敏度的热流体陀螺具有十分重要的意义。本文设计了一种新型单热源热流陀螺仪,该陀螺具有小尺寸的“十”字型腔体,可使热敏电阻产生明显的温度差;同时将两根加热丝并联构成单热源,既能降低功耗,也能保证加热温度不至于过高。为了降低传感器的制作成本,缩短研发周期,提高传感器的性能,在制作流片之前,需要对传感器的敏感机理及影响传感器性能的诸因素进行大量的理论研究。本文通过COMSOL Multiphysics 建立有限元模型,计算单热源热流陀螺仪在有无角速度时的温度场和等温线的变化情况,研究该新型结构陀螺的敏感机理,为该陀螺后续的结构改进、性能优化奠定理论基础。
1 结构原理
新型单热源热流陀螺仪的结构主要由盖板、基底和敏感元件组成,其三维结构如图1 所示。敏感元件含两根并联的加热丝H1、H2和两对平行的热敏电阻TD1和TD2、TD3和TD4,加热丝和热敏电阻均由同一温度系数的铂材料构成。加热丝由相同频率的周期性方波驱动,可产生对称分布的热流。两根加热丝并联构成单热源,这样设计既能减小加热丝的热损耗,也能防止在加热过程中温度过高造成芯片损坏。两对热敏电阻可检测施加Z轴角速度时热流引起的温度变化,敏感Z轴角速度。“十”字型腔体与盖板共同构成热流的工作空间,其优点是利于热流的均匀流动,热敏电阻可产生明显的温度差,便于角速度的检测。单热源热流陀螺仪的剖面图如图2 所示。

图1 单热源热流陀螺仪结构示意图Fig.1 Structure of single heat source thermal flow gyroscope

图2 单热源热流陀螺仪剖面图Fig.2 Profile of single heat source thermal flow gyroscope
新型单热源热流陀螺仪的工作原理如图3 所示。在没有角速度时,H1、H2通电加热,产生对称分布的热流,腔内的温度分布对称,TD1和TD2、TD3和TD4上的温度相同,温度差为零,如图3(a)。当在Z轴施加逆时针的角速度时,对称分布的热流会受到科氏力的作用,向相反的方向偏转,TD1和TD2、TD3和TD4产生相反的温度差[4],如图3(b)。定义:

图3 单热源热流陀螺仪原理图Fig.3 Principle of single heat source thermal flow gyroscope
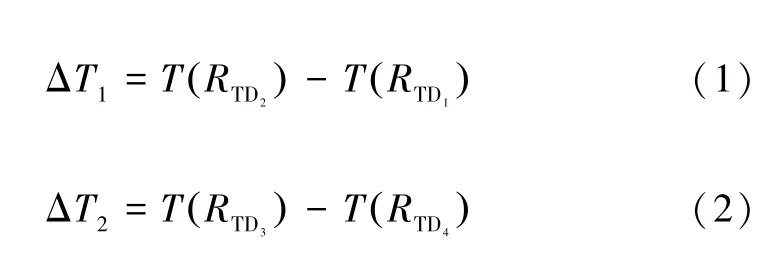
式中:T(R(i))为热敏电阻R(i)的温度;i为TD1和TD2、TD3和TD4中的任意一个[7];ΔT1为热敏电阻TD1和TD2的温度差;ΔT2为热敏电阻TD3和TD4的温度差。
温度差的平均值可由以下公式计算:
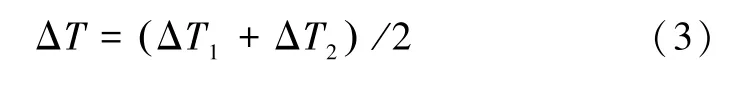
式中,ΔT为两对热敏电阻温度差的平均值。
两对热敏电阻TD1和TD2、TD3和TD4分别与参考电阻Rref连接组成两组惠斯通电桥,如图4 所示;两组惠斯通电桥分别与差分放大器连接,两路信号通过求和放大器,得到输出电压Vout。

图4 两对热敏电阻的读出电路原理图Fig.4 Principle of readout circuit for two pairs of thermistor
输出电压Vout计算公式为:
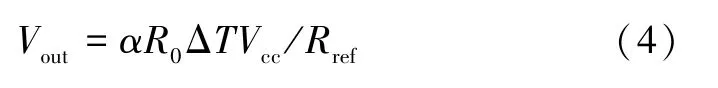
式中:R0是热敏检测丝的初始电阻值;α是铂丝的电阻温度系数;Rref是平衡惠斯通电桥的参考电阻;Vcc是电桥的输入电压[5]。通过公式(4) 可得输出电压Vout。
当角速度ωz为零,ΔT1=ΔT2=0,ΔT=0,Vout=0;当角速度ωz不为零且方向为逆时针,ΔT1>0,ΔT2>0,ΔT>0,Vout>0;若角速度ωz不为零且方向顺时针,则ΔT1<0,ΔT2<0,ΔT<0,Vout<0。
综上所述,单热源热流陀螺的输出电压不仅与两个热敏电阻之间的温度差有关,还与输入角速度大小有关,则有:

由公式(5)可知,通过热敏电阻的温度差可得到相应的输出电压,根据输出电压可计算出Z轴角速度的大小。
2 物理模型
当热源加热时,腔体内的气体在重力场和Z轴角速度的联合作用下产生自由对流,热流沿着工作空间的Y轴产生中心对称的温度分布[9]。而在Z轴方向上,同一X-Y平面内的热敏电阻对Z轴温度梯度的敏感是相同的,因此对于Z轴陀螺来说重力场的影响可以忽略[7]。为简化模型和方便计算,在模型中仅选取敏感元件所在的X-Y平面进行二维建模。单热源热流陀螺仪的物理模型如图5(a)所示。
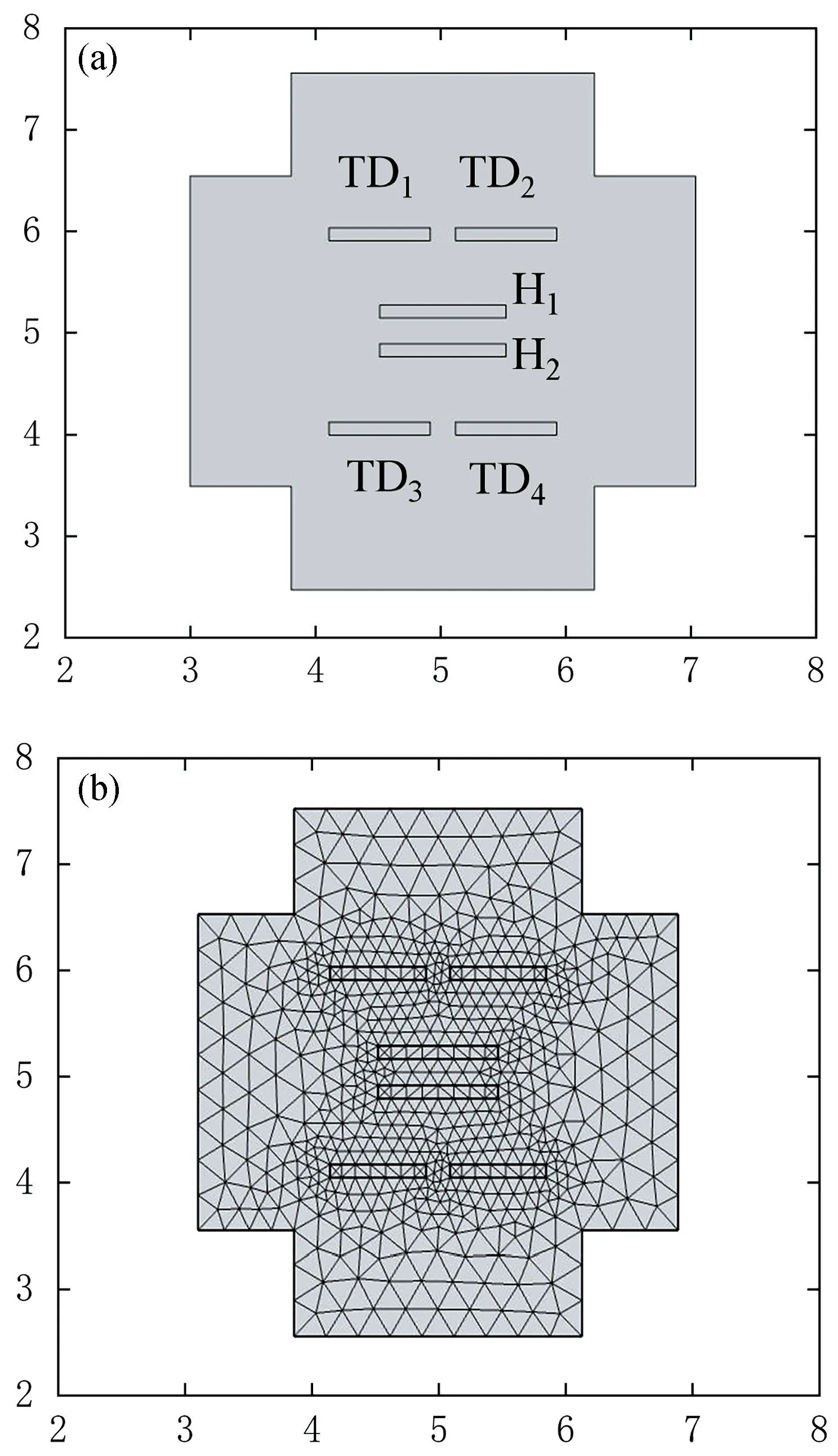
图5 (a)二维仿真模型及(b)网格划分Fig.5 (a)Two-dimensional simulation model and(b) mesh generation
3 数学模型
单热源热流陀螺仪腔体内部的气体流动和温度变化过程符合质量方程[6]、动量方程[7]、能量方程[8]和状态方程[9]:


式中:ρ、、μ、ωz、cp、T、k、P和R分别为气体密度、速度矢量、动力粘度、角速度、比热容、气体温度、导热系数、压力和理想气体常数。
4 有限元法求解
在确立物理模型和数学模型后,通过有限元法利用COMSOL 软件对陀螺的敏感元件在有无角速度时温度场的变化情况进行分析和计算。其求解过程如下:
(1)建立有限元模型[10]。建立如图5(a)所示的有限元模型。热源加载的驱动信号为周期性变化的方波信号,设置研究类型为瞬态。
(2)模型参数设置。对敏感元件部分设置加热丝和热敏电阻的材料、密度、导热系数及定压比热容。对腔体部分设置工作气体的密度、比热容及导热系数。设置热源驱动信号的占空比、频率和幅值。最后,设置沿Z轴方向的输入角速度,其大小为ωz=10 rad/s。
(3)物理场选择。在敏感元件腔体内部,因热源加热引起温度场的变化,选择共轭层流物理场,其中包括固体和流体传热、层流两个物理场。系统会在多物理场中自动生成非等温流动物理场。
(4)划分网格。网格划分质量会影响计算精度、计算时间及收敛性,为了节省计算时间和降低对计算机的要求,网格的单元尺寸设定为常规。网格划分结构如图5(b)所示。
(5)计算。定义瞬态研究的计算时间单位和时间步长后进行计算。
5 计算结果和讨论
随着热源的不断加热,敏感元件腔体内部的温度必然会发生变化[5]。由于H1、H2的温度变化相同,仅分析热源H1处的温度变化。方波的周期为0.2 s,热源H1温度升高的时间和温度下降的时间均为0.1 s。热源温度的计算结果如图6 所示,在1 s 内热源H1处的温度也随着时间变化呈现规律性波动式的增长,1 s内热源温度提高了0.43 K(TH1为热源H1的温度)。

图6 热源H1处的温度变化Fig.6 Temperature change at heat source H1
在无角速度输入时,温度场和等温线的计算结果如图7 和图8 所示。图7 为热源H1、H2加热时陀螺密封腔体内温度场的变化情况,图8 为热源H1、H2加热时陀螺密封腔体内等温线的运动情况。在t=0.1 s,腔体内温度均匀分布;在t=1 s,腔体内温度达到热平衡。根据计算结果分析可知,在无输入角速度的条件下,热源加热产生的热流对称地流向热敏电阻,两对热敏电阻的温度位于同一等温线上,其温度变化是相同的,所以两对热敏电阻温度差的平均值ΔT=0。

图7 热源H1、H2加热时陀螺温度场的运动情况Fig.7 The motion of gyro temperature field when heating by heaters H1 and H2
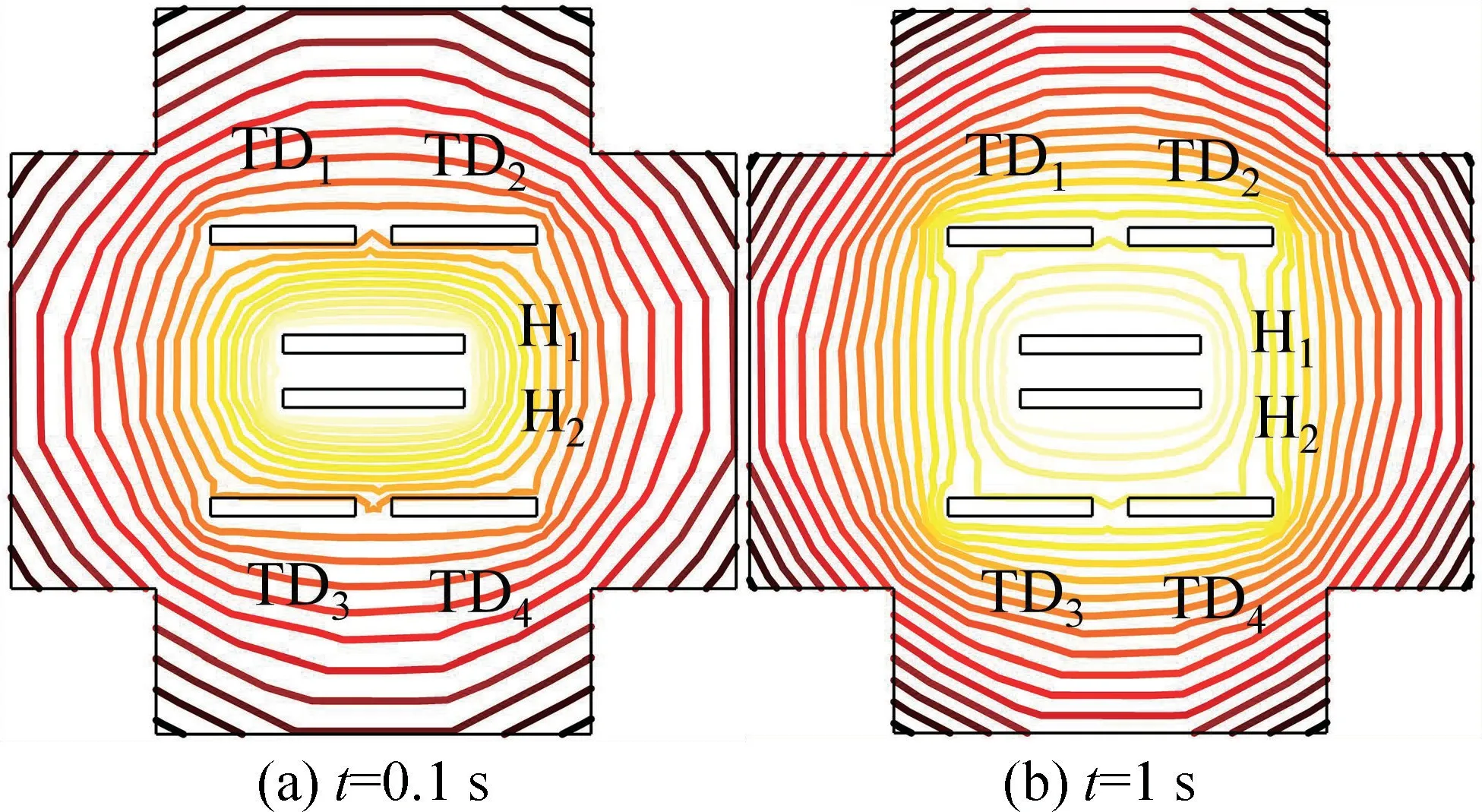
图8 热源H1、H2加热时陀螺等温线的运动情况Fig.8 The motion of gyro isotherms when heating by heaters H1 and H2
当角速度为10 rad/s 时,ΔT1和ΔT2的变化曲线如图11 所示。其中ΔT1为TD1和TD2的温度差曲线,ΔT2为TD3和TD4的温度差曲线。由此可得,单热源热流陀螺仪的二维仿真模型能够敏感温度差的变化,且TD1和TD2的温度差在T=0.06 K 温度范围内上下波动,TD3和TD4的温度差在T=0.05 K 温度范围内上下波动,热敏电阻总的温度变化为ΔT=0.055 K。
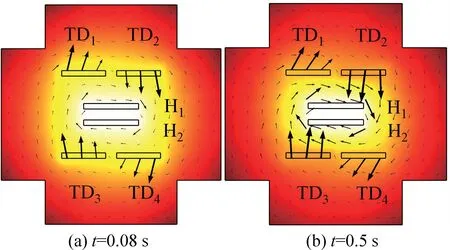
图9 ωz=10 rad/s 时,热源H1、H2加热时陀螺温度场的运动情况Fig.9 The motion of gyro temperature field when heat source H1 and H2 are heated at ωz=10 rad/s
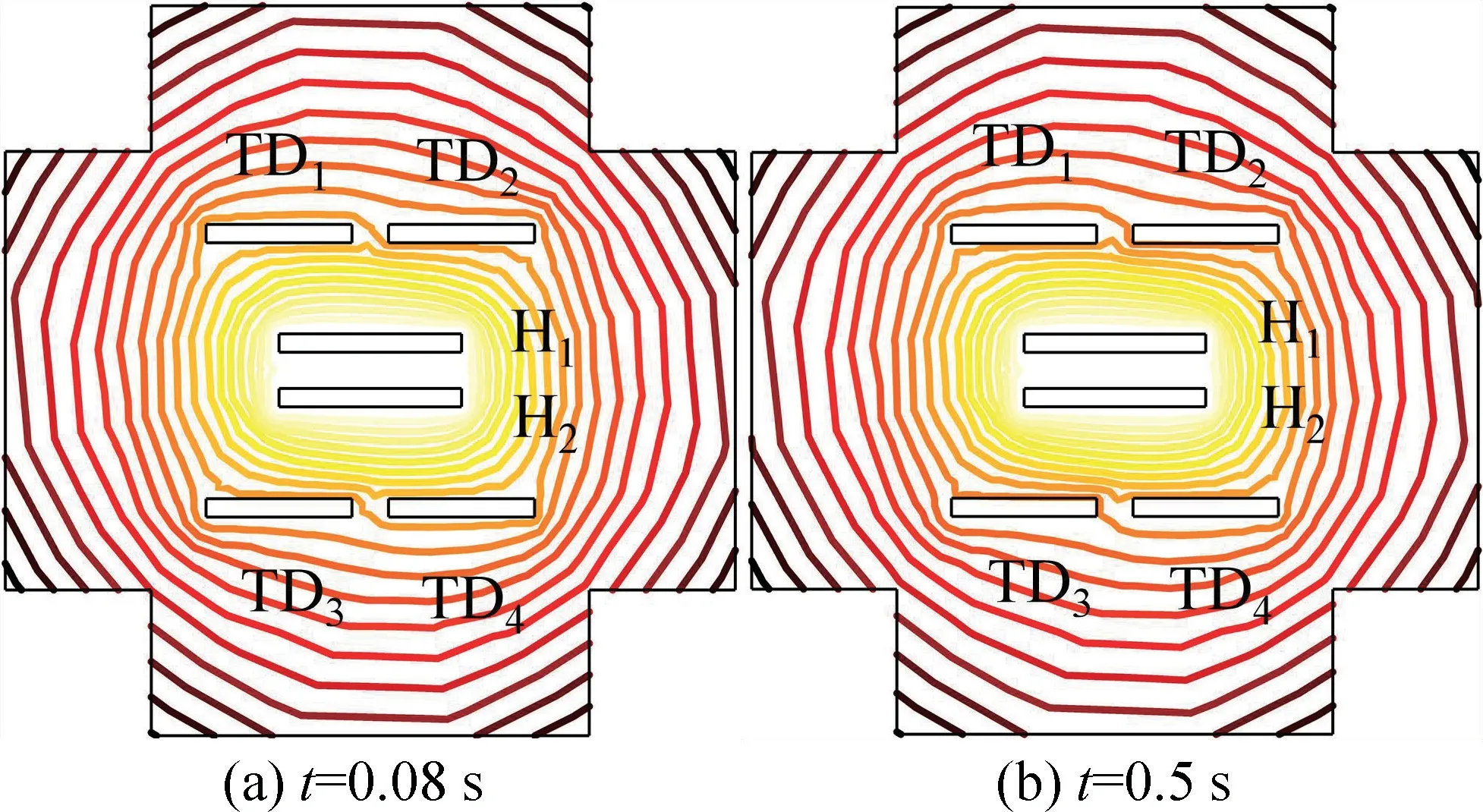
图10 ωz=10 rad/s 时,热源H1、H2加热时陀螺等温线的运动情况Fig.10 The motion of gyro isotherms when heat source H1 and H2 are heated at ωz=10 rad/s
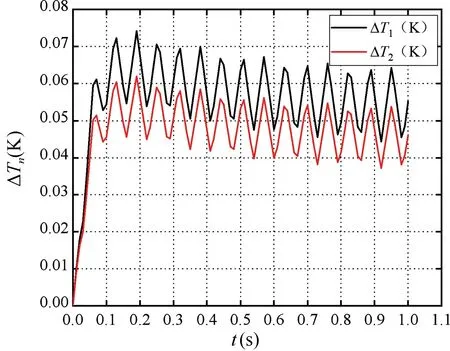
图11 ωz=10 rad/s 时,ΔT1和ΔT2的变化曲线Fig.11 The changes curves of ΔT1 and ΔT2 at ωz=10 rad/s
设单热源热流陀螺仪的输入角速度与热敏电阻的平均温度差满足关系式:
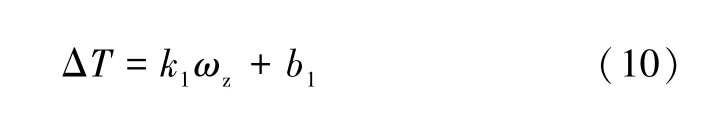
设热敏电阻的平均温度差与输出电压满足关系式:
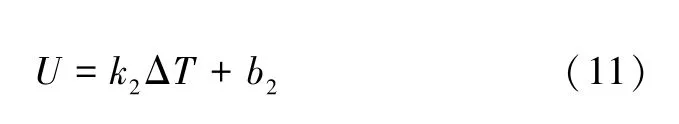
则单热源热流陀螺仪的输入角速度与输出电压满足关系式:

设比例系数k=k1k2,截距b=k2b1+b2,图12 为经过最小二乘法的线性拟合后,单热源热流陀螺仪的灵敏度拟合直线。由该图可知,关系式的比例系数为k=0.005 V/(rad·s-1),截距b=0.005 V,其输入输出关系式为:

图12 陀螺的灵敏度拟合直线Fig.12 Sensitivity fitting line of gyroscope
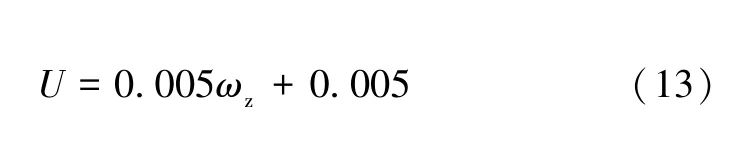
结果表明,在±20 rad/s 角速度范围内,两个热敏电阻之间的温度差的平均值ΔT随角速度的增加而线性增加。因此,在±20 rad/s 角速度范围内单热源热流陀螺仪具有陀螺效应,其灵敏度为5.29×10-3V/(rad·s-1),非线性度为6.81%。由于该模型未考虑重力场[6]对陀螺非线性度造成的影响,因此会造成温度差曲线和拟合直线存在一定的偏差。
6 结论
本文提出了一种单热源热流陀螺仪,介绍了其结构和原理:利用两根加热丝并联,形成一个周期性加热的单热源;利用两对对称分布的热敏电阻来检测Z轴角速度作用下引起的温度变化,从而检测Z轴角速度。同时,利用COMSOL Multiphysics 对该陀螺进行了有限元分析,得到了其腔室内气体在无角速度和有角速度时温度场和等温线的运动情况。计算结果表明,单热源热流体陀螺仪的角速度与输出电压成正比,具有陀螺效应。经最小二乘法的线性拟合后,单热源热流陀螺仪的输入角速度与输出电压的比例系数k为0.005 V/(rad·s-1),灵敏度为5.29×10-3V/(rad·s-1),非线性度为6.81%。与现有的微机械热流陀螺仪相比,该陀螺具有抗冲击能力强、结构简单、成本低、功耗低[11]等优点,可应用于导航、汽车电子、便携式电子设备[12]等领域。
