耗能连梁采用新型复合阻尼器后对剪力墙结构性能的影响

2021-07-05何晴光

兰州理工大学学报 2021年3期

何晴光, 尚进, 党育,2

(1. 兰州理工大学甘肃省土木工程防灾减灾重点实验室, 甘肃兰州 730050; 2. 兰州理工大学西部土木工程防灾减灾教育部工程研究中心, 甘肃兰州 730050)

现代高层建筑越来越需要具备震后可快速恢复的能力,使用消能减震技术是提升高层建筑结构震后可快速恢复功能的一种有效方法[1].何晴光等[2]提出了一种新型自复位耗能摇摆柱,可用于加固改造已有结构及震后遭到破坏的结构.徐飞等[3]对一种新型卷边PEC柱的抗震性能进行研究,结果表明该新型柱具有良好的耗能能力、自复位效果和安全冗余度.

剪力墙结构是高层建筑的主要抗侧力体系,而连梁作为抗震第一道防线,其震后功能能否快速恢复、有效降低震后经济损失是亟待解决的问题.鉴于此,可更换连梁[4]在剪力墙结构中研究与应用越来越广泛.辛辛那提大学Fortney等[5-6]最早明确提出连梁“保险丝”的概念,并将保险丝放置于连梁中,进行往复试验.结果表明,连梁破坏集中于保险丝部分,耗能能力强,便于震后修复与更换.圣母大学Kurama等[7-8]提出了一种将后张拉、无黏结预制联肢剪力墙的钢连梁与混凝土墙肢连接的可更换连梁,通过钢绞线把连梁和墙肢相连,并在连接处安装角钢.地震作用下,通过角钢的塑性变形耗散地震能量.檀国大学Chung等[9]研究了一种摩擦耗能装置,通过对三种不同连梁的剪力墙进行非线性时程分析,得出安装摩擦阻尼器的剪力墙结构具有更好的抗震性能.多伦多大学Lyons[10]开发了一种新型黏弹性阻尼器,该阻尼器将黏弹性材料和约束钢板组合在一起,黏弹性材料会随着约束钢板的运动而运动,并依靠通过黏弹性材料的剪切变形来耗散能量.周云[11-12]研制的钢管铅芯阻尼器,综合应用了铅芯挤压、剪切变形和钢管屈服三种耗能机制.通过对阻尼器进行往复荷载试验和疲劳性能试验,证明该阻尼器耗能性能稳定、滞回曲线饱满.刘少波等[13]基于泡沫铝/聚氨酯复合材料研制出能够发挥黏弹性阻尼器和摩擦阻尼器各自耗能特点的摩擦阻尼器(AF/PU摩擦阻尼器),通过对阻尼器进行性能试验和疲劳性能试验,研究得出AF/PU摩擦阻尼器具有较高且稳定的阻尼比,且滞回曲线饱满.

关于可更换连梁的研究依旧在不断深入,连梁阻尼器在工程上更是具有良好的应用前景.本次研究将针对课题组的发明专利:叠合齿形钢板黏弹性剪切型耗能阻尼器,利用ABAQUS有限元软件,提出一种可以有效代表其性能的等效力学模型,并与仿真模型进行对比验证.再将其应用于高层剪力墙结构的连梁中,进行罕遇地震下的动力时程分析,研究复合阻尼器的抗震性能.以钢筋混凝土连梁刚度为参照,研究了复合阻尼器替换刚度比的取值对结构减震效果的影响,为类似工程的消能减震设计提供参考依据.

1 等效力学模型在ABAQUS中的实现

1.1 叠合齿形钢板黏弹性剪切型耗能阻尼器基本构造及耗能原理

叠合齿形钢板黏弹性剪切型耗能阻尼器(以下简称复合阻尼器)是一种专门安装于连梁跨中的可更换部件[14],该复合阻尼器由黏弹性材料、齿形约束钢板、软钢钢板、连接角钢、普通螺栓、可更换端板组成.薄钢板和橡胶材料交替叠合后经高温硫化而成为复合黏弹性体,软钢钢板通过连接角钢及普通螺栓与两端端板相连,如图1所示.

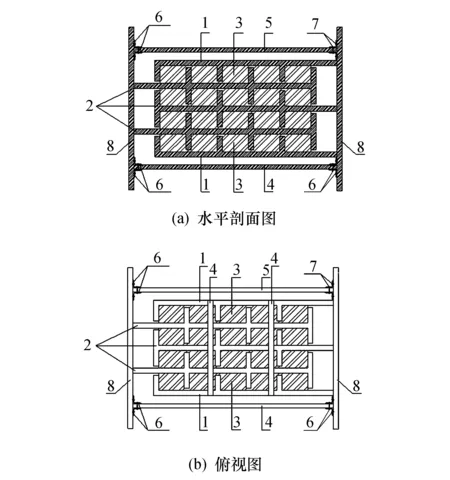
1.外包约束钢板;2.中间约束钢板;3.黏弹性材料;4.预应力钢板;5.软钢钢板;6.连接角钢;7.普通螺栓;8.可更换端端板图1 叠合齿形钢板剪切耗能型阻尼器构造Fig.1 Drawing of shear energy-dissipative damper with the tooth type of superimposition

复合阻尼器的耗能原理：在多遇地震下,保持弹性状态,可以为剪力墙及连梁提供刚度；在罕遇地震下,剪力墙发生弯曲及轴向变形,使连梁发生竖向相对变形,此时连梁会带动复合阻尼器两侧的齿形钢板产生竖向运动,使黏弹性材料和软钢钢板联合工作产生剪切变形,共同消耗地震能量.

1.2 复合阻尼器有限元仿真模型

文献[15]依据专利文献[14]中的设计方法,利用ABAQUS有限元软件,建立了不同构造参数、不同性能参数的仿真模型并进行了模拟加载研究.表1和图2所示的是其中一种构造参数的仿真模型.结果表明,复合阻尼器滞回曲线饱满、耗能性能稳定、耗能能力强,充分利用了低屈服点软钢的剪切滞回变形和黏弹性材料的剪切滞回变形两种机制耗能.当连梁两端相对位移较小时,阻尼器中低屈服点软钢处于弹性阶段,黏弹性材料耗能；当连梁两端相对位移较大时,软钢进入塑性耗能阶段,软钢与黏弹性材料共同耗能,但以前者为主,且塑性阶段耗能性能稳定,由于阻尼器中特有的齿状咬合设计,使阻尼器齿间有较大的相对变形能力.在复合阻尼器规格尺寸按实际连梁需求确定后,可通过调节黏弹性材料厚度和层数、软钢板厚度、软钢屈服点及软钢开缝形式实现连梁阻尼器不同性能的需求.

表1 阻尼器构件参数

图2 复合阻尼器仿真模型Fig.2 Simulation models of composite dampers

1.3 等效的简化力学模型

上述仿真有限元模型单元分格精细包含数千个单元且单元类型复杂,虽然可以实现对构件性能进行比较准确的模拟,但在结构分析中采用多个这样的精细有限元模型时会使计算工作量大为增加,不利于结构整体设计计算.为实现复合阻尼器工程应用,有必要采用一种等效的简化模型替代上述精细有限元模型.本次研究基于ABAQUS有限元平台,提出模拟复合阻尼器的等效力学模型,使简化模型与有限元模型二者在耗能性能上基本一致后,实现在结构分析中代替后者并提高计算效率的目标.等效力学模型由平移连接器(Translation type):Slot单元与Springs/Dashpots单元组合而成,如图3所示.Slot单元与Springs/Dashpots弹簧阻尼单元互相垂直.Slot单元代表复合阻尼器中的软钢材料;Springs/Dashpots单元代表复合阻尼器中的黏弹性材料.在Slot单元属性中输入初始刚度和屈服力值即可定义软钢材料的剪切滞回性能；在Springs/Dashpots单元属性中输入黏弹性材料的等效刚度和等效阻尼值即可定义黏弹性材料的剪切滞回性能.

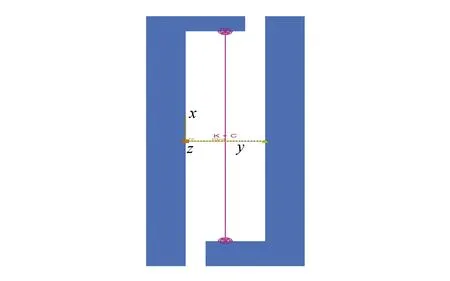
图3 等效简化模型

虽然两种单元联结方向不同,但可以在定义单元参数时对出力方向进行规定使二者并联工作.定义软钢材料的剪切行为时,特别要设置Slot单元的局部直角坐标系.Slot单元虽水平放置,但其剪切位移为竖向,因此定义局部坐标系x轴为竖向,表示Slot单元可沿局部坐标系x轴运动,连接Slot单元的两点相对位移不变.

1.4 滞回曲线

将文献[15]中对表1、图2所示的仿真模型模拟得到的滞回曲线进行力-位移关系转化,计算出Slot单元的初始刚度约为52 kN·mm-1、屈服力为22 kN；经过大量试算模拟,得出Springs/Dashpots单元的等效刚度系数为8 500 kN·m-1、等效阻尼系数为4 600 kN·s·m-1.

对等效力学模型施加频率为0.3 Hz、幅值分别为2.2 mm和5 mm的连续剪切荷载,如图4所示.各加载5圈后,提取力、位移数据,绘成滞回曲线,并与仿真模型对比,如图5所示.从图中可以清楚地看出,滞回曲线反映了黏弹性材料和软钢的特征,且等效力学模型与仿真模型的滞回曲线基本吻合,特别是进入屈服阶段吻合程度较高,故提出的等效力学模型可以很好地模拟复合阻尼器的剪切行为.图5也表明不同位移幅值下复合阻尼器的滞回曲线形状相似,说明阻尼器的性能比较稳定.

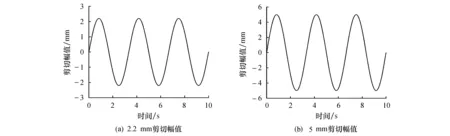
图4 加载曲线Fig.4 Amplitude curve of monotone loading

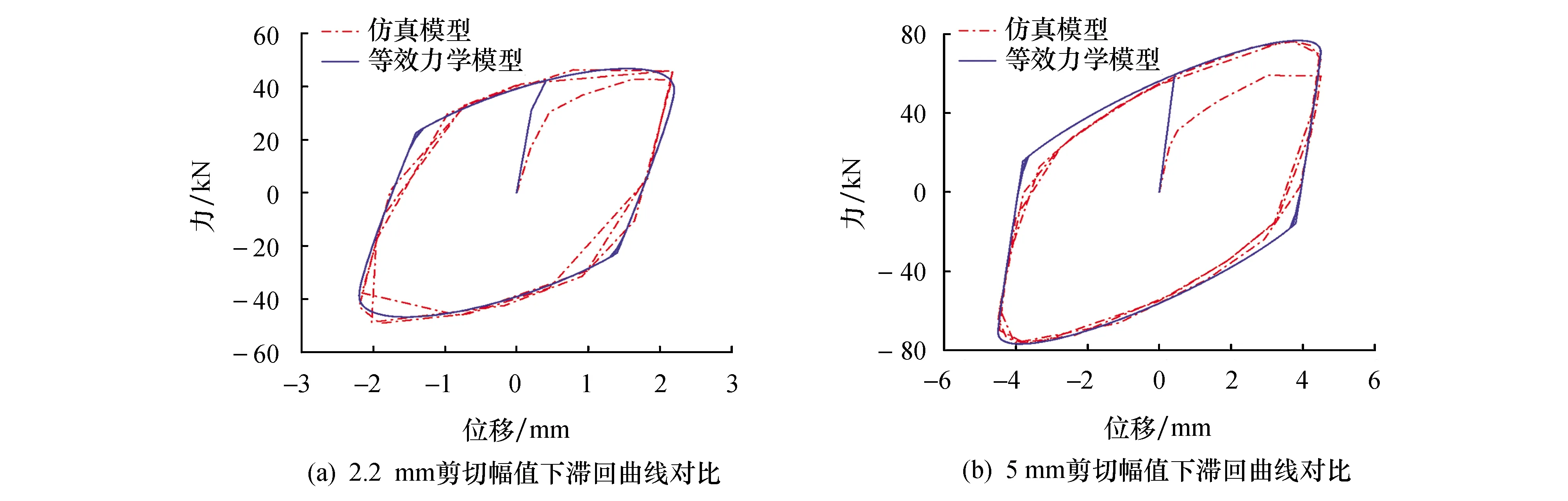
图5 滞回曲线对比Fig.5 Comparison of hysteresis curves

2 复合阻尼器减震性能

2.1 模型概况及选用地震波

根据现行规范,利用PKPM软件设计一立面及平面布置规则的高层剪力墙结构.结构所在区域属于8度(0.20g)抗震设防区,设计地震分组第一组,Ⅱ类场地土,特征周期为0.35 s,剪力墙的抗震等级为二级.结构信息如图6、表2所示.

表2 剪力墙结构楼层信息

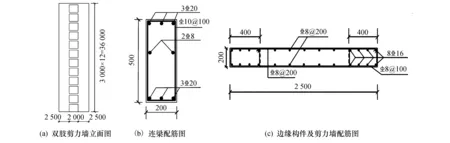
图6 结构配筋和部件

基于PKPM设计结果,利用ABAQUS有限元软件,分别建立传统双肢剪力墙模型(记为TW结构)与设置可更换复合阻尼器的剪力墙模型(记为NW结构)进行抗震性能对比分析,复合阻尼器设置在剪力墙的各层连梁跨中.

从美国FEMA-P695报告[16]中建议的22条地震动记录中选择了7条地震波进行动力弹塑性时程分析,所选地震动信息见表3.采用峰值加速度(PGA)作为地震动强度(IM)指标,依据规范对各地震动按8度大震(0.40g)进行调幅,并取各结构在7条地震动下的最大均值响应进行分析.

表3 地震动信息

对TW、NW结构模型进行模态分析,得到基本周期(括号内为经验值[17]),见表4.两个模型的基本周期值均在经验值范围内,算例模型具有工程代表性,也说明装有复合阻尼器的NW结构模型由于连梁的改变使整体刚度有所下降.

表4 模型基本周期

2.2 弹塑性时程分析

2.2.1层间位移角

提取两个模型在7条波下的层间位移,计算出最大层间位移角均值,绘制成沿楼层高度变化的曲线,如图7所示.可以看出两个结构的弹塑性层间位移角都小于规范限值,同时可以明显看到装有复合阻尼器的NW结构层间位移角小于TW结构,可见复合阻尼器在减小结构整体刚度的情况下仍然可以对整个结构的变形实现较好的控制效果.

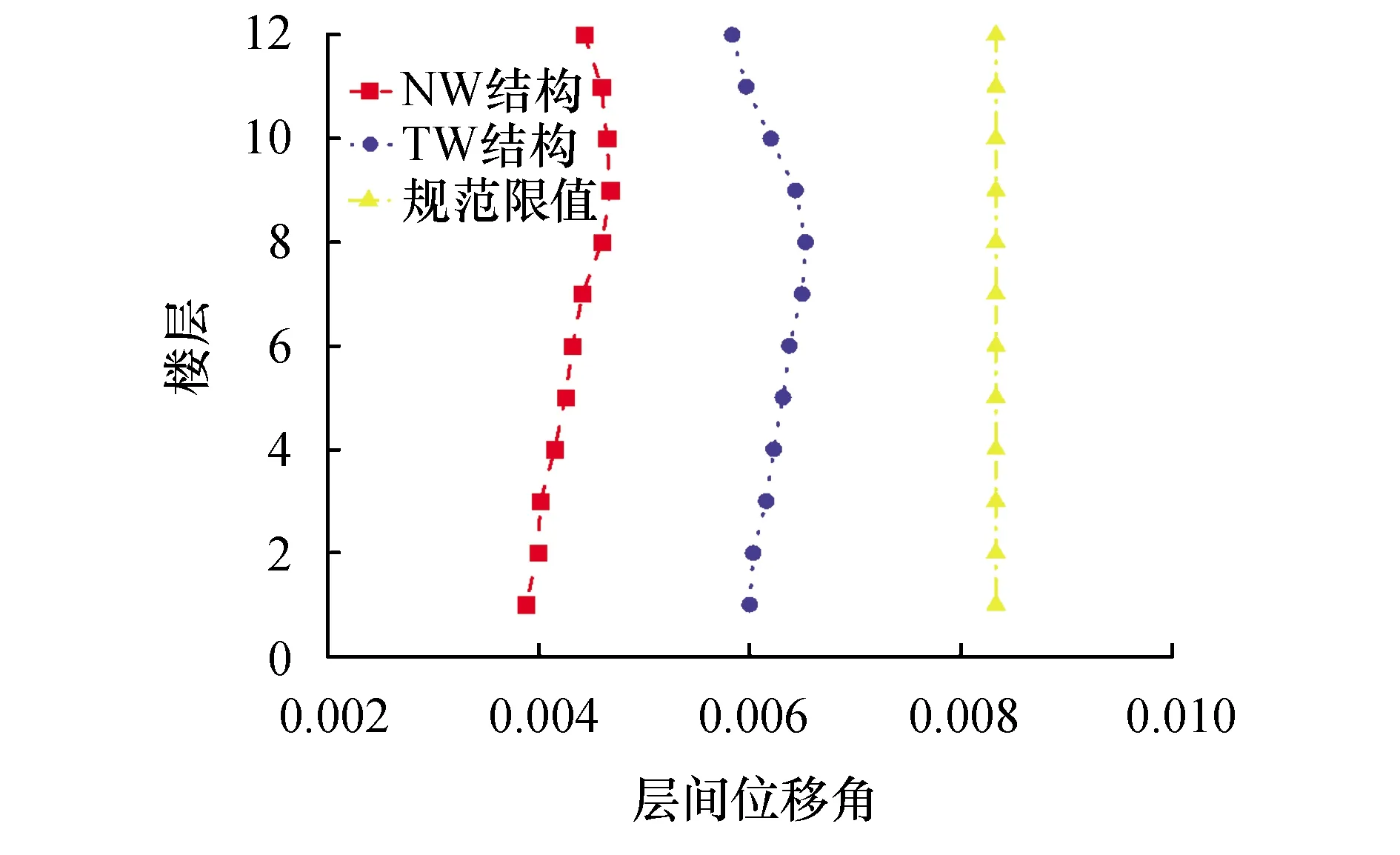
图7 层间位移角

2.2.2基底剪力

TW、NW两个结构基底剪力对比结果见表5.结构布置复合阻尼器后基底剪力有明显的降低,结构的最大减震率为32.01%,最小减震率为24.87%.并且以Northridge-1地震波为例,给出两个结构基底剪力时程曲线对比情况,如图8所示.设置复合阻尼器可更换连梁的剪力墙结构，从而有效减小结构基底剪力.

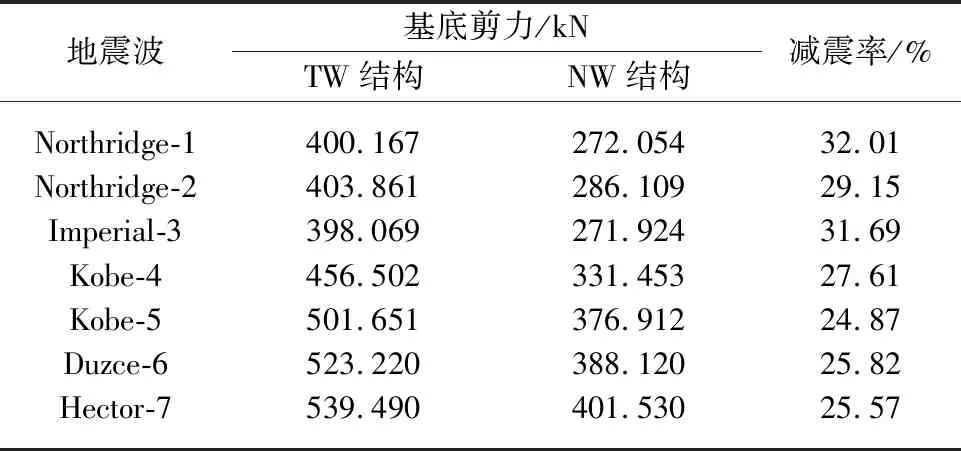
表5 基底剪力对比

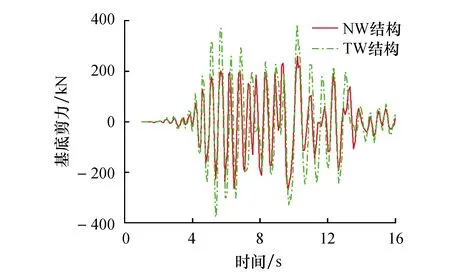
图8 基底剪力时程曲线

2.2.3连梁损伤

可更换连梁的特点就是使连梁的塑性变形主要集中在连梁阻尼器上,这有利于震后对阻尼器进行更换.借助ABAQUS程序中的损伤分析工具,采用混凝土损伤本构可以定义结构的受拉损伤变量(DAMAGEC)和受压损伤变量(DAMAGET),本文利用这两个指标来比较TW、NW两个结构的连梁损伤情况.混凝土的受压、受拉损伤因子取值见文献[18].图9显示了TW、NW两个结构在Kobe-4波的作用下,可更换连梁和传统连梁的等效塑性应变云图.从图中可知,传统连梁的各部分基本进入了塑性状态,不利于震后的维修与加固.而在NW结构中连梁变形集中在复合阻尼器上,非屈服段基本保持弹性,从而实现震后的替换和易修复.

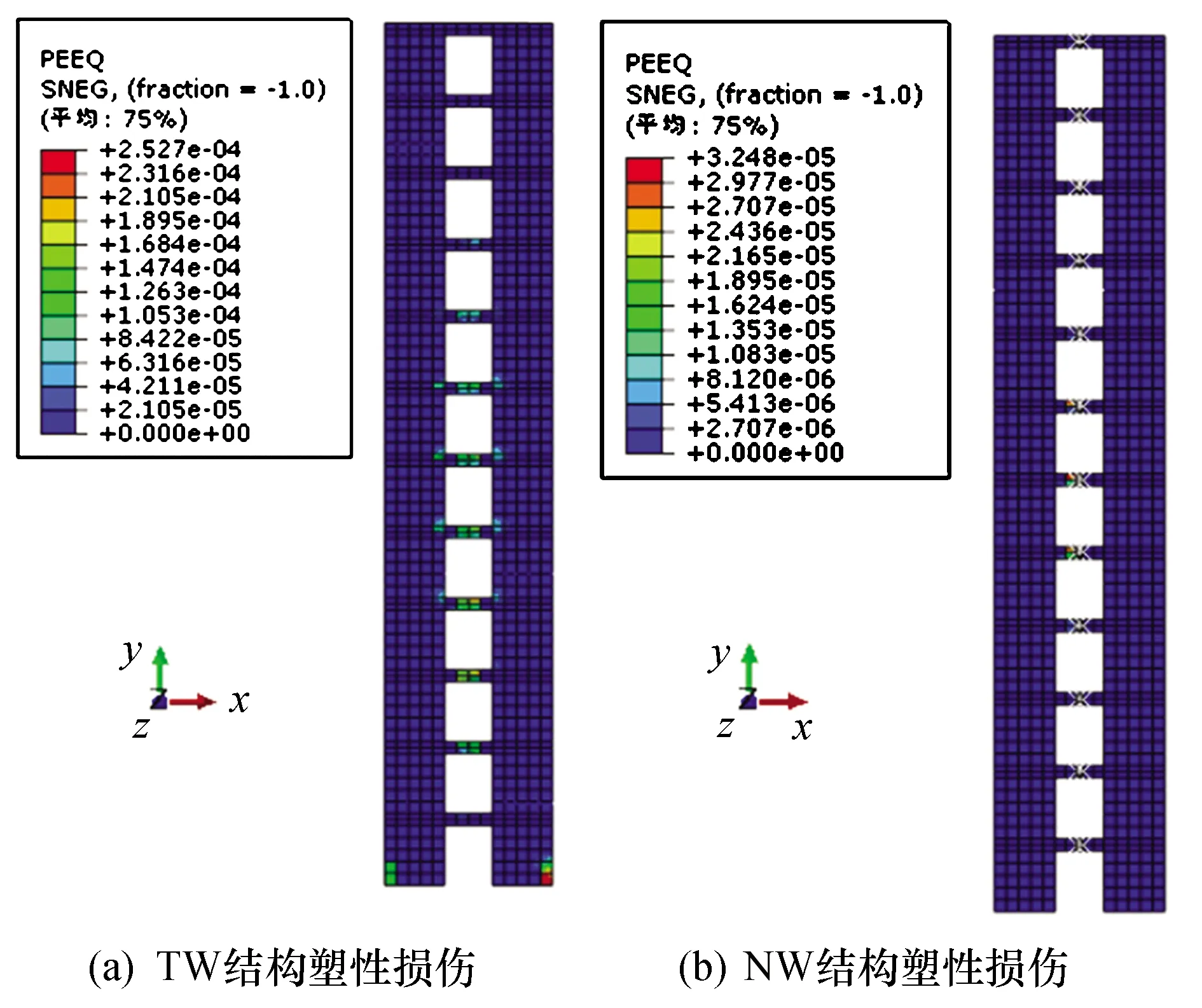
图9 结构连梁塑性损伤云图Fig.9 Equivalent plastic strain of coupling beams

3 复合阻尼器的剪切刚度需求

剪力墙结构中为了使各墙肢可以更好共同工作,连梁通常设计成一个跨高比偏小的构件.安装复合阻尼器的新型连梁要替换传统连梁的功能,必须满足一定的刚度需求.为了便于在工程设计中对1.3节中的等效简化模型参数进行快速合理地设置,以传统连梁的横向刚度作为参考值是容易理解和接受的.另一方面了解连梁安装不同等效刚度的复合阻尼器后对结构地震响应的影响规律,对后期实现工程应用也可以提供有意义的设计参考.

3.1 普通钢筋混凝土连梁横向刚度需求

连梁安装复合阻尼器的目的是替换传统钢筋混凝土连梁的功能.为研究复合阻尼器的刚度需求,建立不同梁高且连梁跨度为3 000 mm的传统钢筋混凝土剪力墙模型.墙肢设计参数同2.1节表2,地震动信息同表3.对各结构进行罕遇地震下的动力时程分析,得到结构最大层间位移角均值,部分模型的计算结果见表6.可以看到对于本模型,当梁高为600 mm时,结构最大层间位移角超过规范限值(1/120)；试算中以50 mm为梁高增量,而当梁高为750 mm时,结构最大层间位移满足规范要求,于是把梁高为750 mm的连梁的横向刚度作为本模型中普通钢筋混凝土连梁的刚度需求.并定义满足罕遇地震时层间位移限值的连梁横向刚度为连梁经济刚度,这里定义的刚度值包含了弯曲变形和剪切变形的影响.

表6 不同梁高的层间位移角

分别利用考虑了弯曲与剪切影响的结构力学公式[19]和ABAQUS有限元软件对截面尺寸为200 mm×750 mm,跨度为3 000 mm的连梁进行刚度计算,得到的连梁横向刚度值见表7.两种计算方法得到的数据相差很小,工程设计时可直接采用有限元计算刚度进行结构计算分析.

表7 刚度对比

3.2 新型耗能连梁的替换刚度比及其影响

在连梁跨中安装复合阻尼器后形成新型耗能连梁,耗能连梁由两侧的普通钢筋混凝土段和中间的复合阻尼器串联而成.为研究新型耗能连梁横向刚度值对结构地震响应的影响程度,定义安装复合阻尼器的耗能连梁的串联刚度与传统连梁经济刚度之比为替换刚度比.

改变复合阻尼器等效力学模型的初始刚度可得到不同初始刚度下新型耗能连梁的串联刚度和经济刚度比见表8,表中复合阻尼器的初始刚度取值参考文献[15]的研究结果.从表中对比结果来看,新型耗能连梁的横向刚度对传统连梁而言取值较小,其意义在于增大连梁的剪切变形能力并使之在剪切往复变形过程中耗能从而保护主体结构.

根据表8,对替换刚度比分别为0.1、0.2、0.3、0.4、0.5的剪力墙模型,进行罕遇地震下的动力时程分析,研究替换刚度比与结构地震响应之间的关系.

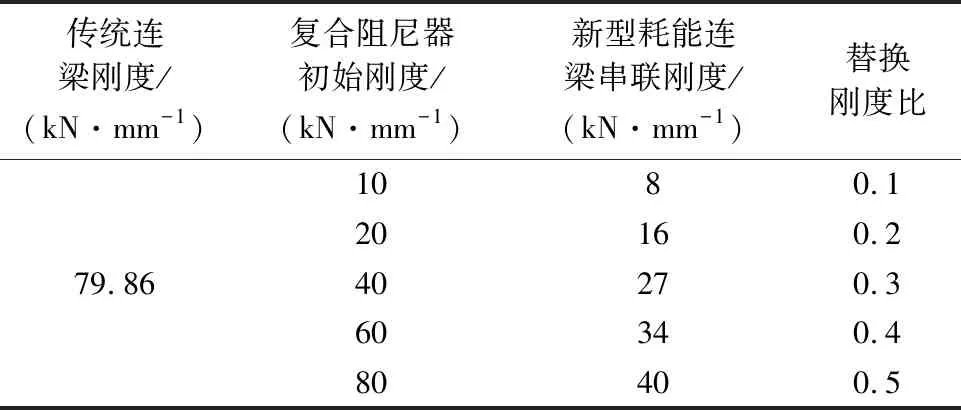
表8 替换刚度比

3.2.1层间位移

结构最大层间位移均值随替换刚度比变化的曲线如图10所示.对比发现,替换刚度比对层间位移影响较大.虽然新型耗能连梁的刚度较传统连梁有所下降,但各层层间位移响应较传统连梁的结构反而有一定减小,当替换刚度比为0.4时,结构每层的层间位移峰值响应最小.

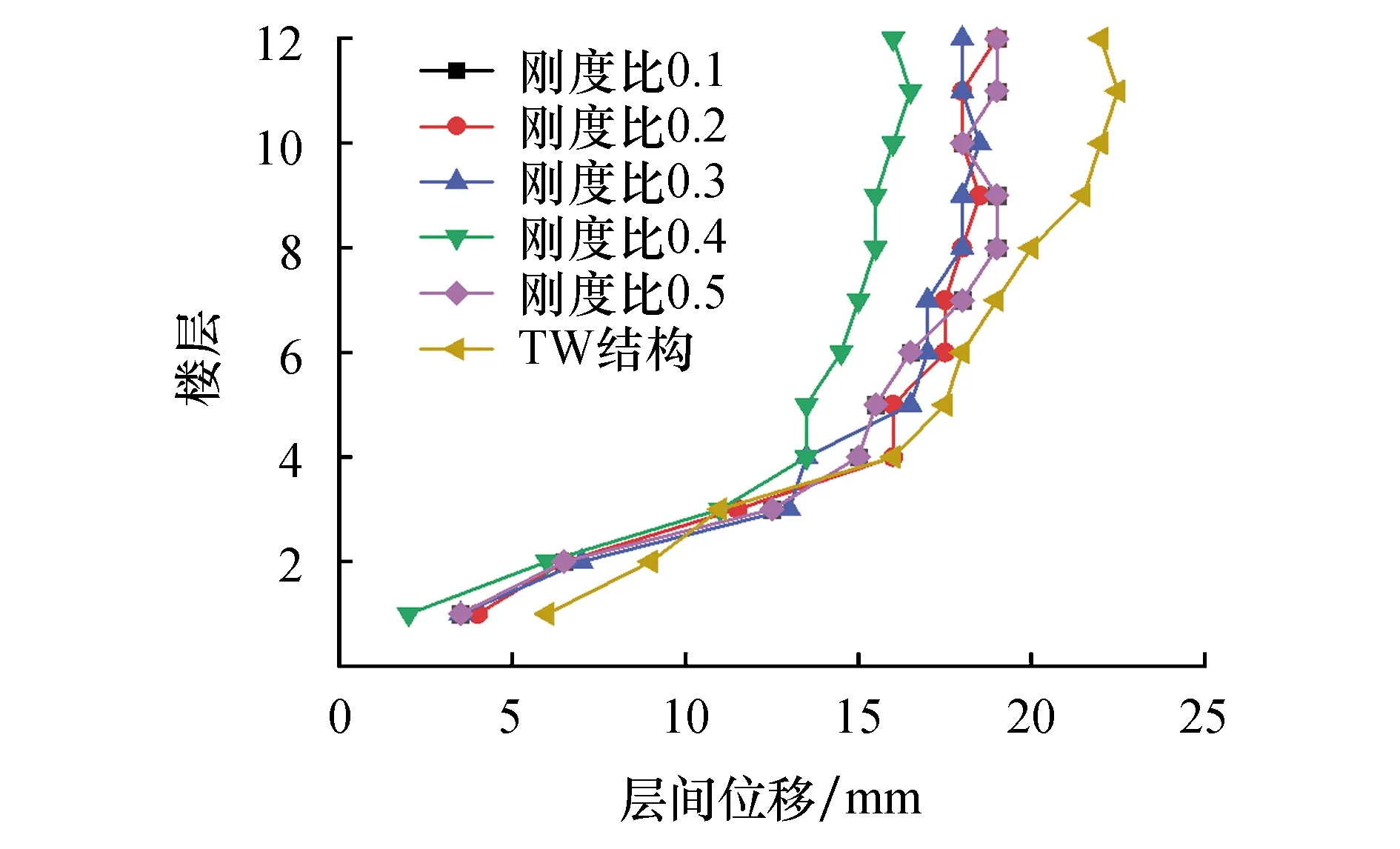
图10 层间位移变化曲线Fig.10 Change of inter-story drifts

3.2.2基底剪力

基底剪力是评价结构所承受地震作用的一个参考指标,统计各地震波作用时的结构最大基底剪力并计算最大基底剪力平均值,绘制结构最大基底剪力均值随替换刚度比变化的曲线如图11所示.从图中可以看出,比较传统连梁的剪力墙而言,采用新型耗能连梁的剪力墙结构基底剪力明显减小.替换刚度比从0.1至0.5逐渐增大过程中,基底剪力呈先减小后增大的变化趋势,且当替换刚度比取0.4时,结构基底剪力值最小.

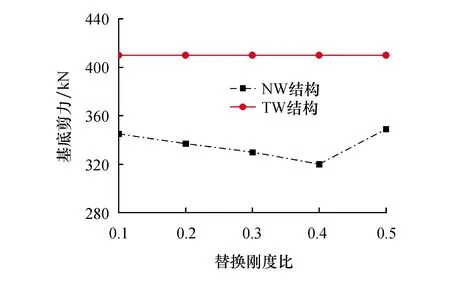
图11 基底剪力变化曲线

3.2.3顶点加速度

结构最大顶点加速度均值随替换刚度比的变化曲线如图12所示.从图中可以看出,顶点加速度随替换刚度比的变化规律与基底剪力随替换刚度比的变化规律一致,当替换刚度比为0.4时,结构顶点加速度峰值响应最小.

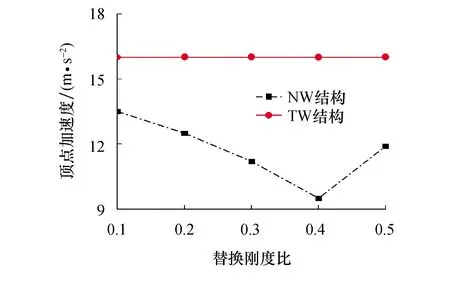
图12 顶点加速度变化曲线Fig.12 Change of peak acceleration

从上述3项性能指标的分析结果中可以看出,新型耗能连梁的刚度值虽然比传统连梁小,却对结构抗震性能有明显的提高,且不同替换刚度比对结构的减震性能改善程度不同.对本文中的模型而言，当刚度比取0.4时,结构获得了更好的减震性能.

3.3 耗能分析

为观察复合阻尼器的耗能过程,选择替换刚度比为0.4的模型,提取结构各层连梁中Slot单元的力与位移值数据,绘成滞回曲线.图13所示为Northridge-1地震波激励下第1层、第6层、第12层中Slot单元的力与位移关系曲线.可以看出复合阻尼器的竖向剪切幅值分别为3.1、6.2、5.1 mm,所有耗能软钢都进入了塑性状态;滞回曲线形态说明软钢材料在罕遇地震时耗能充分；中间楼层连梁阻尼器剪切位移幅值最大,耗能效果最为明显.

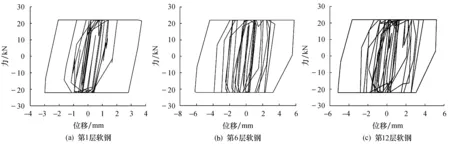
图13 软钢滞回曲线Fig.13 Hysteretic loop of steel

设置复合阻尼器主要是将变形集中于连梁跨中阻尼器处,从而通过阻尼器的变形与耗能减小连梁混凝土的变形与损伤,而复合阻尼器在震后易于维修与更换.以输入Northridge-1波时的响应为例,观测模型在替换刚度比为0.4时混凝土的应变.发现在Northridge-1波作用过程中连梁悬臂段出现的最大主拉应变约为2.4×10-4,最大主压应变仅为1.8×10-5,说明连梁跨中在安装复合阻尼器后两侧悬臂段一直处于弹性工作阶段.