基于图论的中国高铁网节点中心性进化研究

祝延波

(青海民族大学 物理与电子信息工程学院, 青海 西宁 810007)

高铁以高速、大容量、集约型、通勤化的特征,在中等距离的出行上具备极强的竞争力.中国高铁快速发展,许多大中小城市因高铁而串联,客流、物流、资金流在城市间、地区间的流动更加便捷和高效.高铁网络正以前所未有的速度改变、影响着中国城市的格局,一座座高铁沿线城市正在崛起.随着中国高铁建设的深入进行,中国越来越多的城市开始进入高铁时代.截至2019年底,中国铁路营业里程已经达到13.9万km,其中高铁3.5万km,居世界首位.2019年全球高铁客运量为35亿人次,其中中国21.5亿人次,占比超过60%.高铁时代,城市边界被打破,空间距离被淡化,时间距离成为主要标尺[1-3].

中国高铁的诞生和发展促进了城市间的竞争和融合,缩短了地理空间距离,极大地促进了人民群众出行方式、工作方式、生活方式乃至思维方式的变革,也极大地推动了中国社会的发展,中国高铁成为中国一张靓丽的名片,向世界展示着中国速度和中国魅力.同时,随着高铁网的不断延伸和完善,高铁影响半径不断延长,各类资源在交通节点、交通干线、交通圈内重新分配,区域内的经济联动更加密切.随着兰新高铁、沪昆高铁、广昆高铁、京港(台)高铁、呼南高铁、包(银)海高铁、兰(西)广高铁、沿江高铁、沿海高铁、京兰高铁、厦渝高铁等八纵八横线路的建成通车,中国高铁网通达城市和覆盖范围会进一步扩大,重要性会愈加凸显.

高铁的竞争力和优势显而易见,高铁在中国也得到了迅猛的发展.近年来，图论在各种复杂交通网络如铁路网、公交网、公路网、航线网、轨道交通网等领域得到了广泛应用.本文旨在通过对中国高铁网进行基于图论的复杂网络分析,研究和分析判定重要节点的算法,用网络仿真分析软件 Pajek对这些重要节点的复杂网络特征值、进化过程进行对比分析,确定不同时段的节点重要性量化值,寻找节点重要性波动变化的原因,发现其中的进化特征和规律.

1 相关工作

复杂网络拓扑结构的异质性,导致网络中不同节点对于网络的结构和功能的影响表现迥异.

通过抽象的图来研究复杂网络有助于比较不同网络之间的异同点从而找到其中的共性特征,为分析和研究它们的拓扑性质提供有效算法.网络科学中对节点重要性的度量及排序研究日渐升温[4-5],挖掘各类复杂网络中的重要节点,有针对性地研究其性质特征具有重要意义,网络重要节点挖掘与分析已成为复杂网络理论研究方向的热点.

一个具体交通网络可抽象为一个由点集V和边集E组成的图G=(V,E).V中的每一个点可表示一个具体的交通枢纽,如一个空港、一个公交站点、一个车站、一个城市等.E中的每一条边可以表示连接两个城市、两个交通枢纽、两个车站、两个空港或公交站点之间的路线等.这样就可以将交通网络问题转变为图来进行研究.

一些学者利用图论对公路网、航线网、城市公交网、轨道交通网等交通复杂网络进行研究，取得了较好的效果.于宝等[6]利用站点重要性综合评价指标挖掘中国高铁网的重要站点, 通过计算网络效率和最大连通子图,分析了中国高铁网在随机攻击和蓄意攻击下的表现,但他们的计算主要依据节点度和介数.谌薇薇等[7]构建了基于二阶张量的轨道交通网络的拓扑结构模型,对模型的度和度分布、网络直径、平均路径长度、聚类系数等特征指标进行分析,并用3个中心性指标评价网络节点重要度,然后以重庆市轨道交通网络为例对该方法进行了验证,但论文并未列出评价算法.闫玲玲等[8]对中国航空网节点重要性用5种方法进行了排序和攻击实验,仿真结果表明,基于介数中心性的节点重要性排序方法能够更准确地刻画网络中节点的重要性；并将节点的直接影响力和节点邻居之间连接的紧密程度结合起来,提出了一种基于度和聚类系数的新指标.雷永霞等[9]利用Pajek软件建立了高速铁路客运专线无向加权运输网络模型,分析了该网络模型在随机站点攻击和蓄意站点攻击下的连通鲁棒性和功能鲁棒性评价指标,结果表明中国高铁网络在随机站点攻击下体现出高度的连通鲁棒性和功能鲁棒性,在蓄意站点攻击下体现出高度的连通脆弱性.钟业喜等[10]从流空间理论出发,从网络密度、中心度特征、网络层级特征等方面分析了中国城市高铁网络结构特征,从首位联系、联系强度、结合点轴理论等区域空间结构的相关理论对中国高铁城市网络的地域组织模式进行了深入研究.阮逸润[11]研究了复杂网络单节点与多节点重要性排序问题,提出了一种基于邻域相似度的复杂网络节点重要度评估算法,分别从网络鲁棒性与脆弱性、信息传播动力学的评价角度对网络节点重要性进行了度量.黄建华等[12]提出了具有二维特征的节点重要性评价指标体系,该指标体系综合考虑了网络静态结构和动态网络流两方面的影响因素.

本文通过对中国高铁不同时段通车运营路段的综合分析[1-3],借助网络仿真分析工具Pajek分别构建了基于图论的中国高铁网，如图1～3所示.该网络中的节点为国内各城市高铁站,网络中的边为连接这些高铁站的高铁线路.图1是宝兰高铁通车(2017年7月)后的中国高铁网，图2是截止2020年年初运营中的中国高铁网，图3是规划的2035年八纵八横中国高铁网.

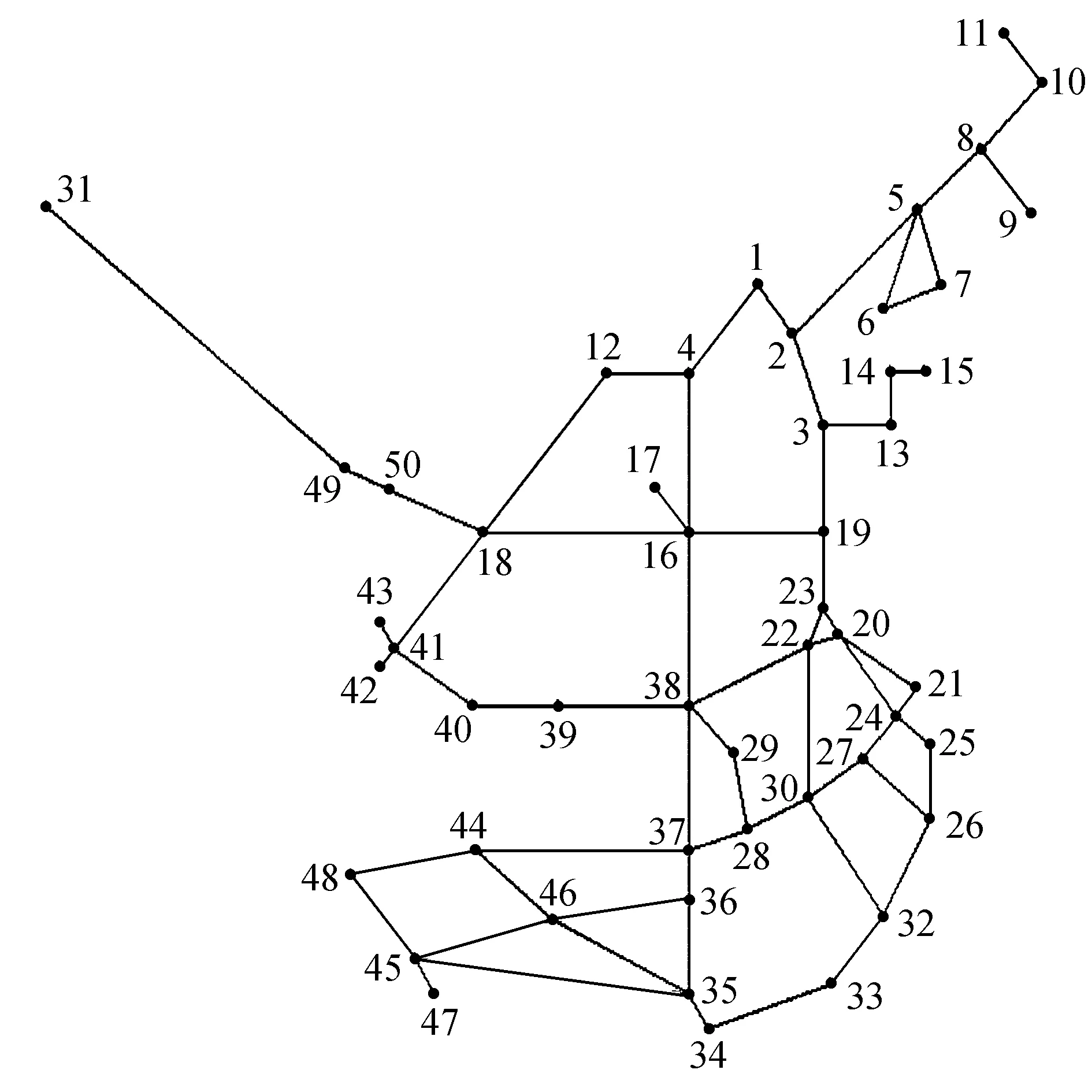
图1 2017年宝兰高铁通车后的中国高铁网

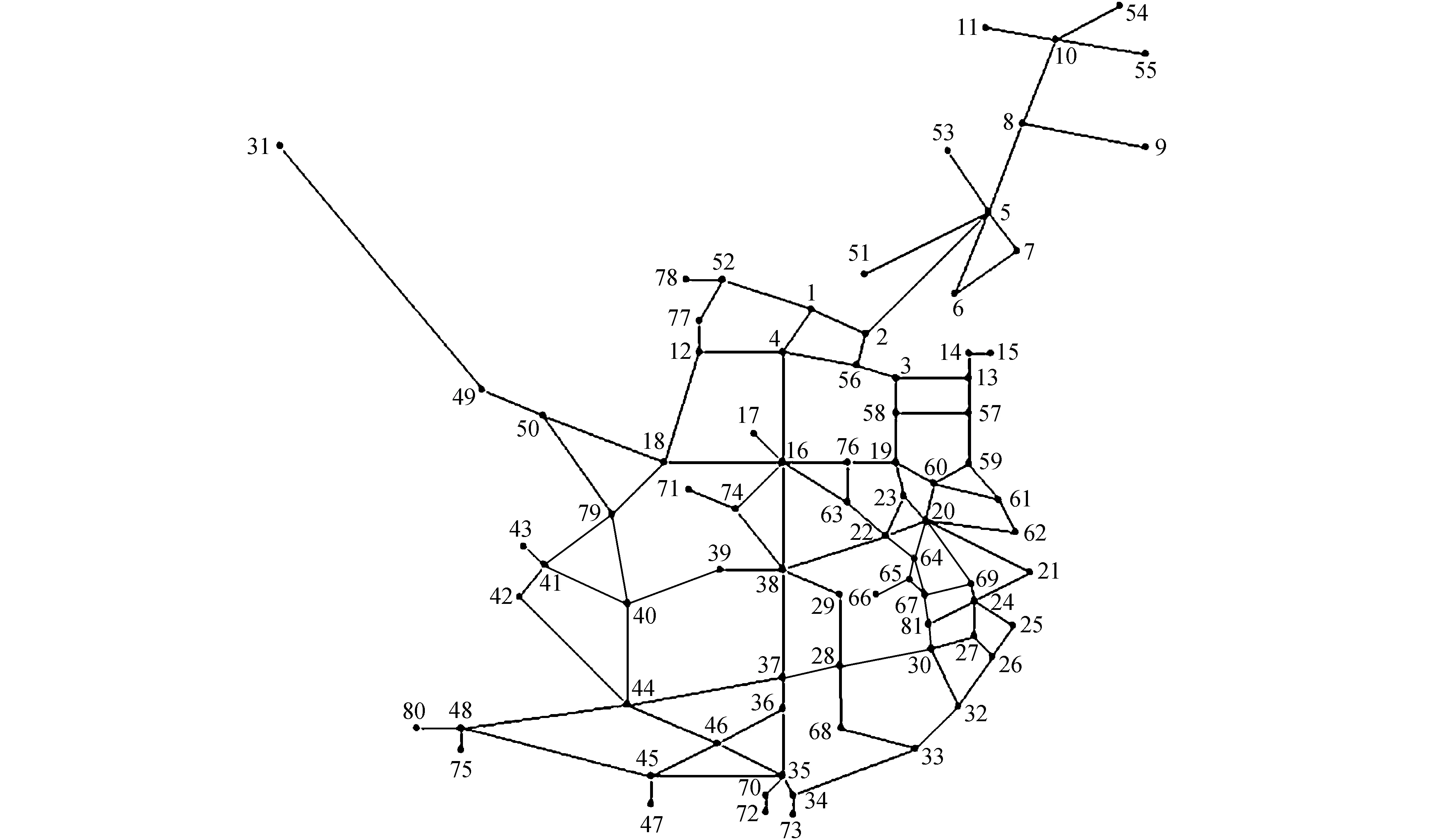
图2 2020年初的中国高铁网

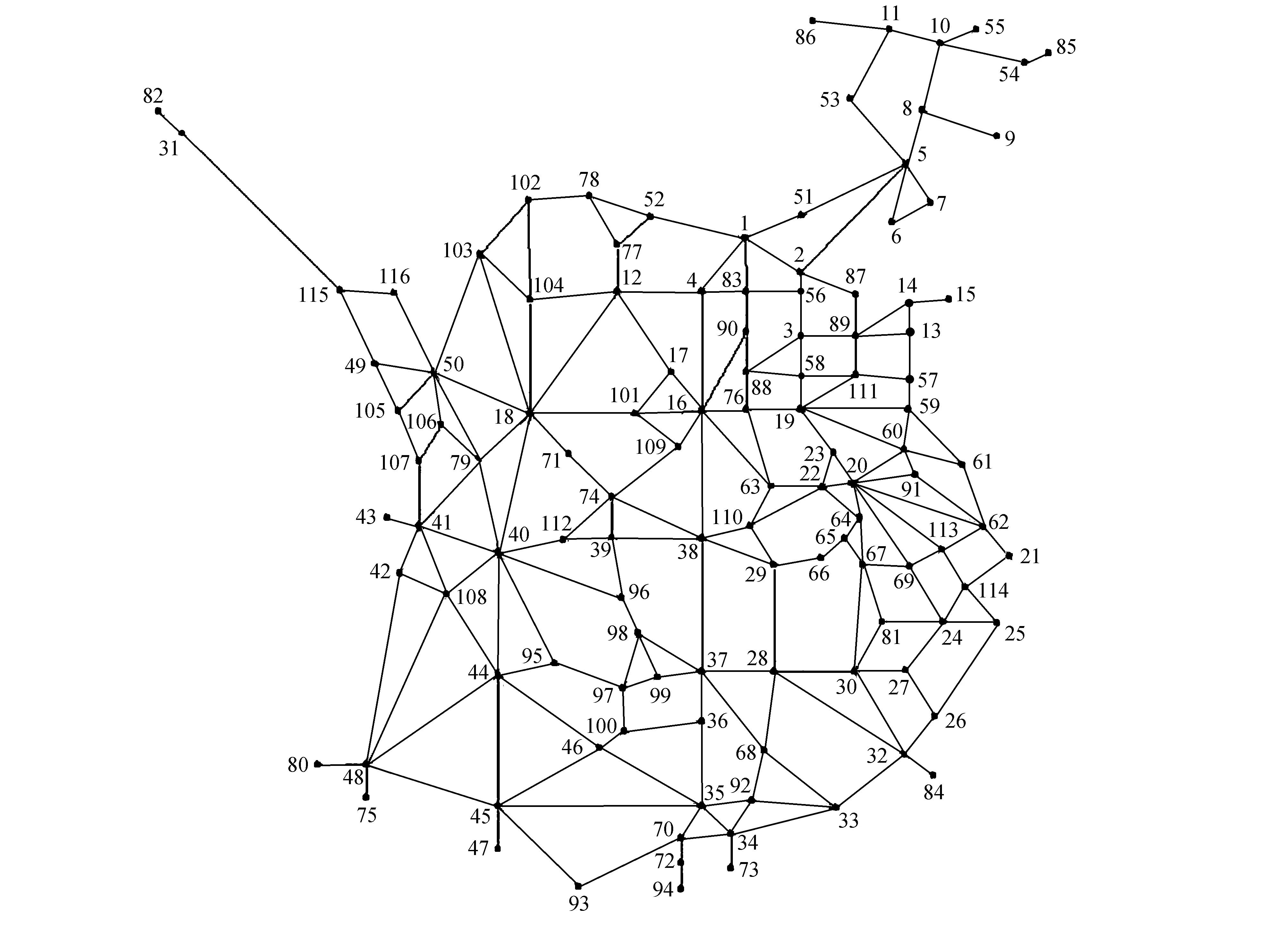
图3 2035年规划的中国高铁网

图1～3中的网络节点编号对应的城市为:北京(1)、天津(2)、济南(3)、石家庄(4)、沈阳(5)、大连(6)、丹东(7)、长春(8)、珲春(9)、哈尔滨(10)、齐齐哈尔(11)、 太原(12)、青岛(13)、烟台(14)、荣成(15)、郑州(16)、焦作(17)、西安(18)、徐州(19)、南京(20)、上海(21)、合肥(22)、蚌埠(23)、杭州(24)、宁波(25)、温州(26)、金华(27)、南昌(28)、九江(29)、上饶(30)、乌鲁木齐(31)、福州(32)、厦门(33)、深圳(34)、广州(35)、衡阳(36)、长沙(37)、武汉(38)、宜昌(39)、重庆(40)、成都(41)、乐山(42)、都江堰(43)、贵阳(44)、南宁(45)、桂林(46)、北海(47)、昆明(48)、西宁(49)、兰州(50)、承德(51)、张家口(52)、通辽(53)、牡丹江(54)、佳木斯(55)、德州(56)、日照(57)、曲阜(58)、连云港(59)、淮安(60)、盐城(61)、南通(62)、阜阳(63)、芜湖(64)、铜陵(65)、安庆(66)、铜宣城(67)、赣州(68)、湖州(69)、中山(70)、十堰(71)、珠海(72)、香港(73)、襄阳(74)、玉溪(75)、商丘(76)、大同(77)、呼和浩特(78)、广元(79)、大理(80)、黄山(81)、霍尔果斯(82)、衡水(83)、平潭(84)、绥芬河(85)、满洲里(86)、东营(87)、菏泽(88)、潍坊(89)、聊城(90)、扬州(91)、惠州(92)、湛江(93)、澳门(94)、怀化(95)、常德(96)、邵阳(97)、益阳(98)、娄底(99)、永州(100)、洛阳(101)、包头(102)、银川(103)、榆林(104)、合作(105)、陇南(106)、松潘(107)、宜宾(108)、南阳(109)、黄冈(110)、临沂(111)、恩施(112)、苏州(113)、嘉兴(114)、张掖(115)、武威(116).

2 节点重要性排序算法

复杂网络本质上的非同质拓扑结构,决定了网络中每个节点的重要程度是不同的,就像一个人在一个机构或部门中扮演的角色和重要性是不同的.一个节点是否重要在不同视角下的评价标准各不相同,一个节点之所以比其他节点更重要,是因为该节点能够在更大程度上影响着网络的结构与功能.

复杂网络重要节点排序算法主要有基于网络拓扑结构和网络传播动力学模型两大类.近年来，国内外基于网络结构的节点排序算法主要有四种：基于节点近邻的排序方法(度排序)、基于网络全局信息的排序方法(接近中心性排序和介数中心性排序)、基于节点位置信息(K-Shell法)的排序方法以及基于随机游走的排序方法(PageRank、LeaderRank与H指数).

网络节点的度中心性指标、聚类系数和介数中心性指标分别从局部、中观和全局视角研究了网络节点重要性.接近中心性指标从一个新的角度考虑,指标值越大的节点在网络中所处的位置越靠近网络中心.

网络节点的度值反映了节点对网络中其他节点的直接影响力；节点的接近度反映了节点到达其他节点的难易程度,是评价节点是否处于网络中心位置的重要指标；节点的介数则反映了节点在网络中的连接作用,是网络中的“桥”节点.

本文选择节点度中心性(degree centrality,DC)、介数中心性(betweenness centrality,BC)、接近中心性(closeness centrality,CC)这三个指标来评估网络中节点的重要性.

定义1度中心性(DC).节点i的度中心性DCi定义为节点i的度值d(i)与网络中所有节点值减1的比值,即：

DCi=d(i)/(n-1)

(1)

定义2介数中心性(BC).网络中经过一个节点的最短路径数越多,则这个节点就越重要.介数中心性为所有最短路径经过节点的路径数目的比率,表示节点对介质传输的控制能力,属于全局特性的指标.节点i的介数中心性BCi计算公式为

(2)

其中：α(s,t)为介质从节点s传输到节点t的最短路径数;α(s,t|i)为介质在s与t间传输过程经过节点i的最短路径数.

定义3接近中心性(CC).接近中心性CC(i)定义为节点i到其他所有节点距离的平均值的倒数.节点i的接近中心性为节点通过传播对其他节点产生影响的能力,由节点到网络中其他所有节点的距离总和的倒数衡量.节点i的接近中心性计算公式为

(3)

针对单个指标无法有效反映网络节点中心性的问题,本文定义网络节点重要性评估指标由度中心性、介数中心性和接近中心性三个指标混合而成,并表示为

K(i)=100×(αDCi+βBCi+γCCi)

(4)

其中:α≥0,β≥0,γ≥0,且α+β+γ=1.由于αDCi+βBCi+γCCi的值为(0,1),在式(4)中将节点重要性K(i)取值设定在(0,100).在评估静态网络节点中心性时,可以根据现实网络的具体特征调整参数α、β和γ的大小,以反映不同评估指标的相对重要性.

图4是各节点在不同时段参数α、β和γ取不同值的得分情况.其中:A组表示参数α、β和γ的取值分别为α=1/3,β=1/3,γ=1/3；B组表示α=0.4,β=0.4,γ=0.2；C组表示α=0.2,β=0.4,γ=0.4；D组表示α=0.4,β=0.5,γ=0.1；E组表示α=0.5,β=0.4,γ=0.1.

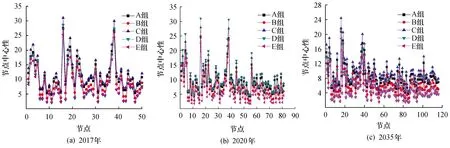
图4 中国高铁网节点重要性Fig.4 Nodes importance of CHSRN

通过对α、β和γ选取满足条件的值进行多次反复仿真实验,发现C组实验由于设定γ=0.4,导致不同时段一些节点如洛阳、益阳、九江、衡阳、宜昌、承德等排名异常靠前,原因是这些节点和网络中的重要节点如郑州、武汉、长沙、北京等相邻,导致这些节点的CC值较大,因此不考虑这组值.通过对A、B两组实验结果分析发现部分节点排名异常,原因与C组实验相似,因此也不考虑A、B 组实验值.

利用Pajek分别计算出图1～3中各节点的度数、介数中心性和接近中心性,结合式(1，4)计算出中国高铁网不同时段的重要节点Top20如表1所列(E组：α=0.5,β=0.4,γ=0.1).

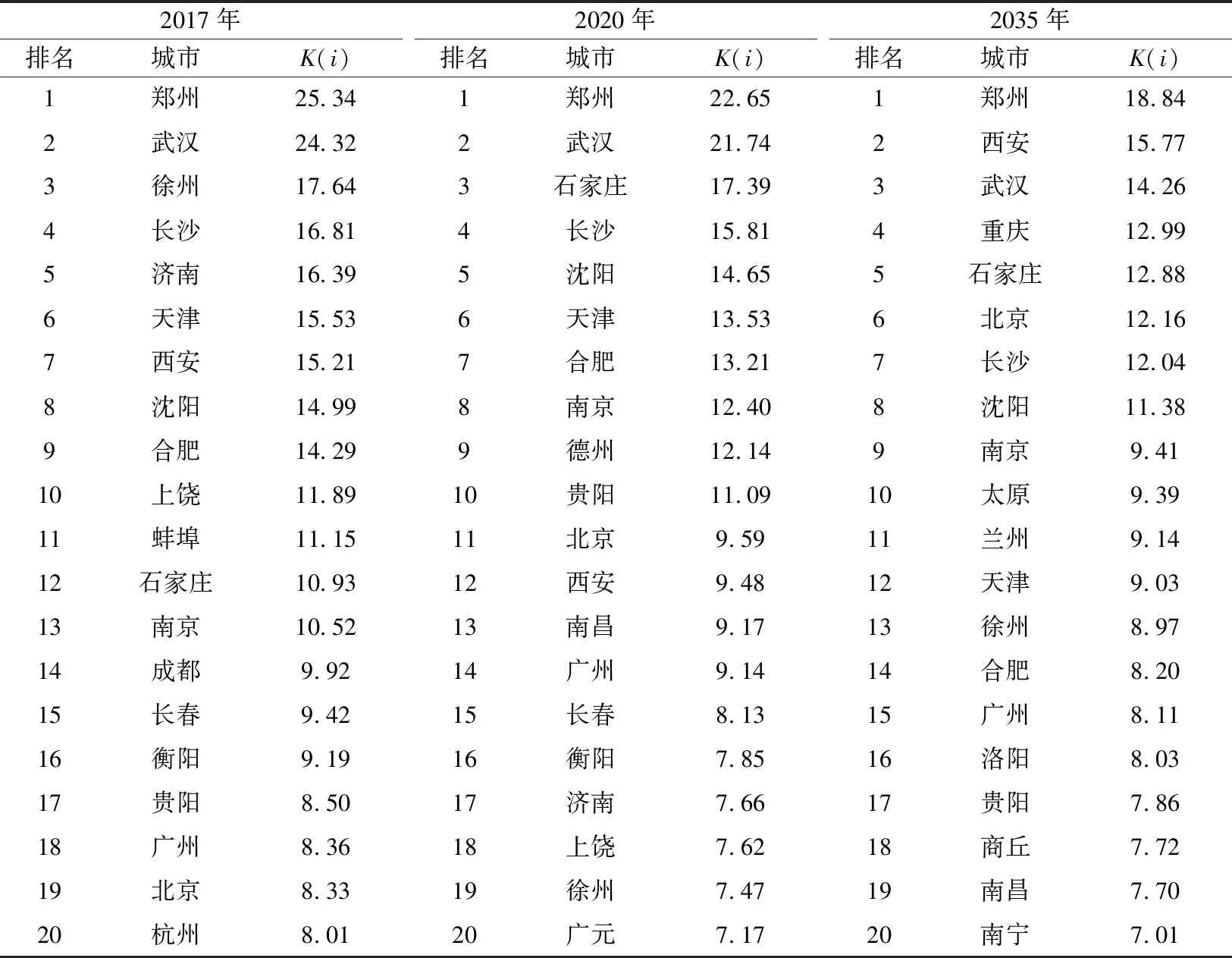
表1 中国高铁网不同时段的重要节点Top20

3 节点重要性进化分析

对表1进行对比分析可以发现,在不同时段,郑州得分均排列第一,这说明在高铁时代,郑州是中国高铁网最重要的核心节点.在不同时段郑州、武汉、长沙、沈阳都排名在Top10,这说明了这些城市在中国高铁网中具有重要的核心枢纽地位.事实亦如此,郑州、武汉、长沙是京广高铁的重要枢纽,同时也分别是陆桥通道、呼南通道、沿江通道、厦渝高铁和沪昆高铁的重要枢纽,从图1～3也可看出这些节点正是京广高铁上最重要的节点.沈阳是京沈高铁、津沈高铁、哈大高铁、沈丹高铁的重要枢纽,是东北诸多城市的必经节点,因此沈阳的排名也较稳定.

此外,南京、北京、西安、广州、天津、石家庄、贵阳、合肥、徐州在不同时段全都位于Top20,这些节点也是中国高铁网的重要站点.北京、广州是京广高铁的两个端点,分别连接京张高铁、京沪高铁、京沈高铁、京港高铁、南广高铁、兰广高铁、广湛高铁、贵广高铁.天津是京沪通道和沿海通道上的重要枢纽,也是进出关的重要枢纽.西安是陆桥通道、京昆通道、包海通道上的重要枢纽,随着国家八纵八横规划高铁线路的完工,西安的重要性超过了武汉和长沙,跃居第二.

石家庄是青银通道和京广通道上的重要枢纽,贵阳是兰广通道、包海通道、沪昆通道上的重要枢纽,合肥是沿江通道和京港(台)通道上的重要枢纽,徐州是陆桥通道和京沪通道上的重要枢纽.济南、南昌、蚌埠、上饶、成都、重庆、长春、德州、广元、衡阳、太原、杭州、南宁、洛阳在不同时段位于Top20, 这些节点也是中国高铁网的重要节点.基于不同时段Top20节点重要性进化过程的分析结果见表2～4.

从表2可以看出,长沙、长春、衡阳排名有所下降；石家庄、北京排名上升较快；南京、广州略有上升；济南、上饶、蚌埠、杭州排名持续下降；徐州、西安、成都排名波动较大(先降后升),主要原因在于三个节点的介数中心性下降较大,然后又回升较多所致(徐州：0.295—0.071—0.108；西安：0.217—0.118—0.250；成都：0.095—0.033—0.041).因为2017年徐州是京沪高铁和陆桥通道的重要枢纽,所以排名很高；2020年随着徐州周边的商丘、淮安、济宁和其他地方的高铁相继开通,徐州的排名下降较大；而随着连徐高铁的通车,徐州作为连接路桥通道、沿海通道、京沪通道的枢纽其作用也进一步凸显,其排名又上升较快.成都排名波动的原因与徐州相似,随着成都周边广元、重庆到兰州、贵阳等地的高铁开通,成都的排名下降较多；随着成昆高铁的通车,成都排名又有较大上升.

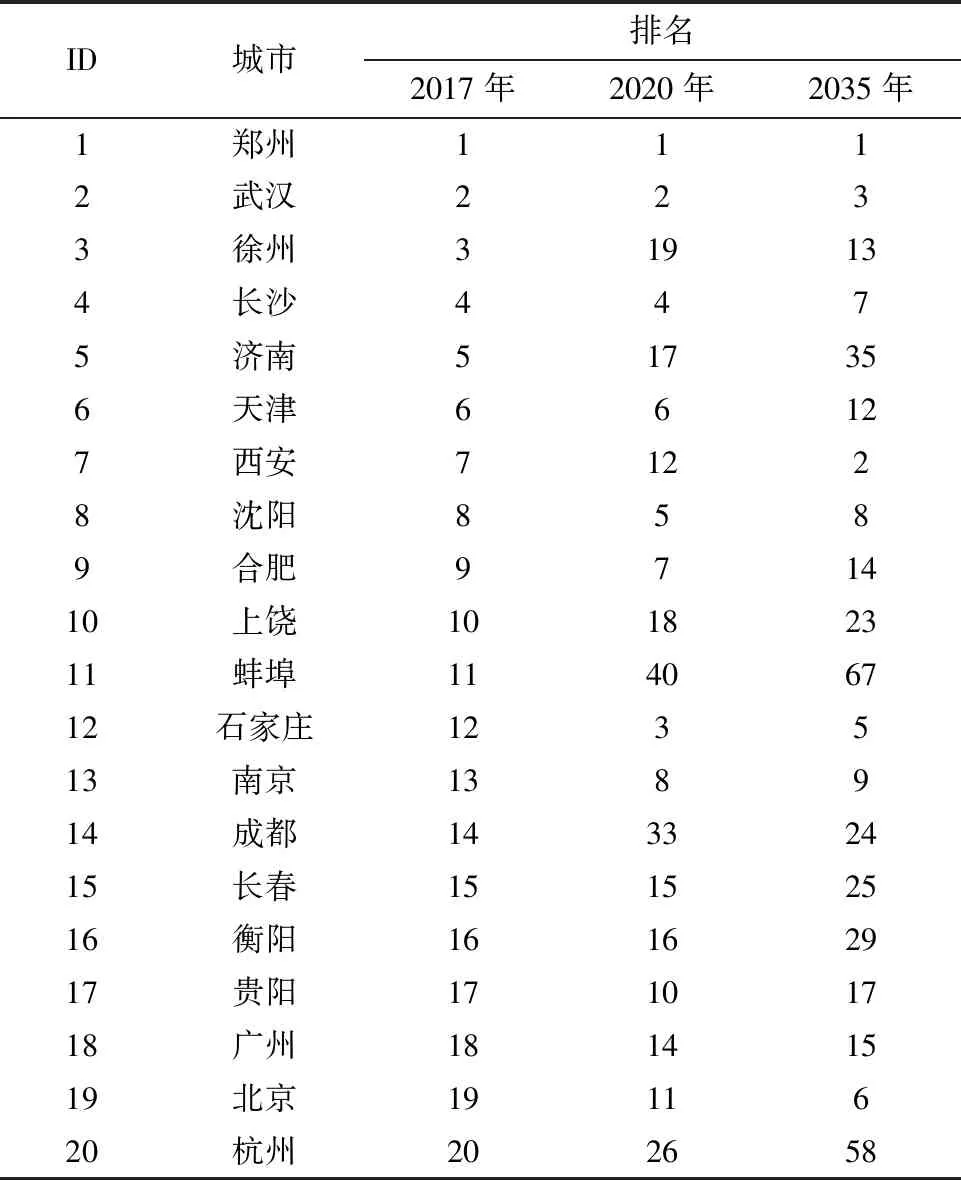
表2 中国高铁网Top20节点进化表(2017年)

天津、长春、衡阳的排名有所下降.而天津的排名下降原因在于京沈高铁通车后,进出关不需绕行天津(天津的介数中心性从0.244降为0.135).长春(介数中心性从0.12降为0.083)、衡阳(介数中心性从0.098降为0.063)排名下降的原因和天津类似,从沈阳可以绕行至哈尔滨.

济南、蚌埠、上饶、杭州的排名有较大的下滑,主要原因是随着高铁路网的完善,其相邻城市开通了其他高铁线路,导致这几个城市介数中心性持续下降(济南：0.272—0.096—0.043；蚌埠：0.137—0.023—0.018；上饶：0.136—0.081—0.057；杭州：0.048—0.045—0.013),最终排名下滑较多.济南排名下滑的另一个原因是随着京港通道的开通,在京沪高铁和京广高铁之间有了一条和它们平行的线路.

石家庄、南京、广州的排名处于先升后降状态.主要原因是随着石济高铁的开通,石家庄成为连接京沪高铁和京广高铁的重要节点(石家庄介数：0.134—0.313—0.219；南京介数：0.102—0.147—0.101；广州介数：0.06—0.104—0.091；石家庄度数：3—4—5；南京度数：4—7—8；广州度数：4—5—6).

北京的排名一直处于上升状态.随着京张高铁、京沈高铁、京港高铁的建成通车,北京的枢纽地位不断增强.这从北京介数中心性变化也可看出来(北京介数：0.101—0.141—0.197).

从表3可以看出,广元的排名有所下降,德州的排名下降较快.主要原因在于2020年前后广元是连接西南、西北高铁线路的唯一枢纽,随着兰成高铁、成西(宁)高铁、西(安)渝高铁的开通,广元的重要性降低了(广元介数中心性从0.203下降至0.027)；随着京港高铁的开通,德州介数中心性下降较多(从0.203下降至0.027).

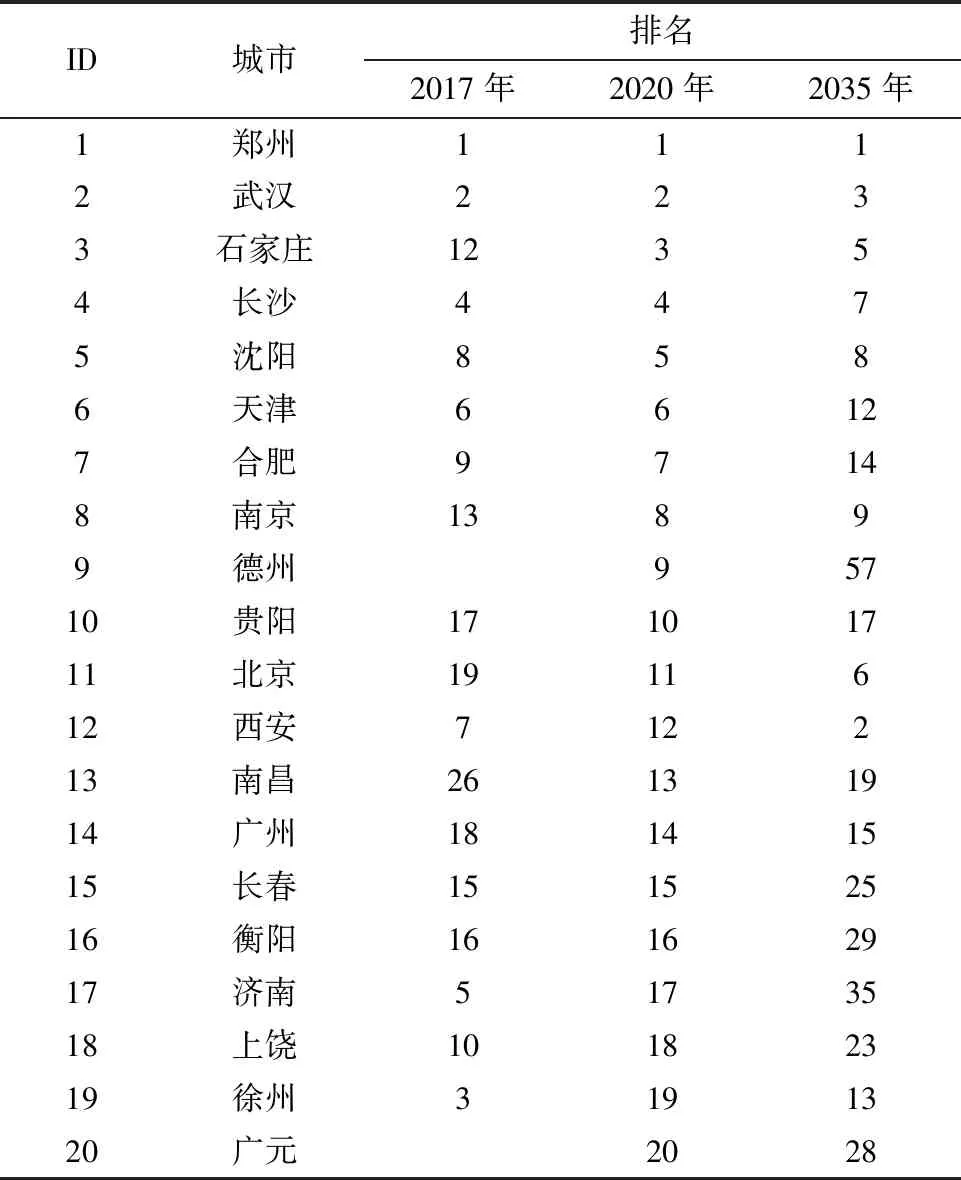
表3 中国高铁网Top20节点进化表(2020年初)

从表3还可以看出,南昌的排名也出现了波动(先升后降),原因与南京、广州类似(南昌的介数中心性：0.032—0.114—0.088).

从表4可以看出,重庆、太原的排名有了较大的提升,这主要是由于西(康)渝高铁、厦渝高铁、湘渝高铁、渝昆高铁、郑太高铁、太(中)银高铁的开通,这些城市的高铁运营线路增加较多(重庆度数：2—4—8；太原度数：2—3—5),介数中心性相应增加较快(重庆介数中心性：0.031—0.057—0.183； 太原介数中心性：0.024—0.053—0.125),节点重要性日益增强所致.

表4 中国高铁网Top20节点进化表(2035年)

从表4还可以看出,兰州、南宁的排名出现波动(先降后升).原因是和2017年相比,2020年兰州、南宁的度数没有变化,2035年则有兰成、兰银、南贵(阳)、南湛(江)等多条高铁线路通车,相应地兰州、南宁的介数中心性也出现波动(兰州介数中心性：0.080—0.049—0.104；南宁介数中心性：0.045—0.033—0.065).

通过对表1～4的分析发现，重要节点排名进化演变有四种主要方式：基本稳定不变(郑州、武汉、长沙、沈阳)；持续上升(重庆、太原、北京)；持续下降(杭州、济南、上饶、蚌埠)；波动，而波动又有先升后降(石家庄、贵阳、德州)和先降后升(徐州、西安、成都、兰州、南宁)两种.

4 结论与讨论

本文基于图论分别构建了不同时段的中国高铁网(图1～3),借助复杂网络仿真分析工具Pajek 对不同时段(2017、2020、2035年)中国高铁网各节点分别进行了复杂网络特征分析(节点度、接近中心性、介数中心性等),针对不同时段分别确定了Top20的重要节点(表1),对这些节点中心性进化过程进行了分析研究(表2～4),分析了这些重要节点排名持续上升、下降或波动的原因.

随着中国高铁网的的逐步完善,呈现出下列特征：

1) 每个节点重要性得分呈逐步下降的趋势.

2) 整个网络的平均度数、特征向量逐渐增加.

3) 整个网络的介数中心性、接近中心性、网络密度均呈现下降趋势.

中国高铁网是一个覆盖范围广、构成多样、地位重要的复杂网络.研究发现，随着八纵八横高铁规划线路(沿海通道、京港通道、包海通道、呼南通道、兰广通道、京兰通道、青银通道、沿江通道、京昆通道等)的完工,一些节点的重要性会有较大的提升,如西安、重庆、太原、兰州、成都、徐州等,原因在于随着这些重要节点度数的增加,其介数中心性也随之增加,节点重要性排名也随之增加了；一些新的重要节点会出现,如上饶、襄阳、聊城、阜阳、赣州、洛阳、商丘等；有些节点的重要性排名有所下降,原因在于随着中国高铁网开通线路的增加,互为备份路段增多,整个路网不断完善,整个网络的鲁棒性不断提高,这些节点的介数中心性下降较多,导致节点重要性降低.部分节点在不同时段排名出现了波动,对这些节点波动的原因本文也进行了分析.

本文的研究主要基于中国高铁网的拓扑结构和节点地理位置,综合考虑节点运量、通达车次、通达线路等业务指标是下一步的研究内容.