h形双排桩在边坡与基坑联合支护中的应用研究

洪世海

(福建省建筑设计研究院有限公司 福建福州 350001)

0 引言

随着我国城市化进程逐步加快，城市建设用地日益紧张。福建省地处丘陵地带，目前平原地区建设用地面积逐渐减少，越来越多工程项目建设于山地。山地建筑在场地平整与主体结构施工过程中需要进行大量边坡与基坑支护工作，因此合理选择边坡与基坑支护型式是山地建筑工程的一个重要课题。

双排桩支护作为一种新型基坑支护结构，已经广泛应用于全国各地的基坑工程。当双排桩中的前排桩桩顶高程低于后排桩时，即形成所谓的h形双排桩支护结构。许多学者及工程技术人员对h形双排抗滑桩在滑坡治理工程中的应用做了诸多研究[1-6]，国家规范《铁路路基支挡结构设计规范》亦有提及椅式双排桩在路基支挡结构中的应用[7]，但h形双排桩支护结构在边坡与基坑支护工程中的研究与应用相对较少。截至目前，h形双排桩支护结构的计算模型与计算方法并未在相关标准与规程中予以明确。本文将依托某实际边坡与基坑联合支护工程，探讨h形双排桩支护结构的计算模型与方法。

1 工程背景

泉州市某安置住宅小区设二层地下室，地下室基坑开挖深度约为10.0 m。拟建场地东侧用地红线存在一高度为6.0 m的陡坎，陡坎坡顶为行车道路与已建民房。由于陡坎临空面位于用地界线之内，需在该侧对陡坎进行切坡开挖，在场地与行车道路之间形成高度6.0 m的永久性挖方边坡。加之场地内地下室基坑开挖，场地东侧将形成高度16.0 m的临时性深基坑，其中，永久性边坡高度约为6.6 m，临时性基坑深度9.4 m。基坑开挖完成后，拟建场地边坡及基坑与周边的位置关系剖面图如图1所示。综合场地地质条件、周边环境及支护结构破坏后果严重性判定，本边坡工程安全等级为一级，基坑支护结构安全等级为一级。

图1 场地东侧边坡及基坑支护型式剖面图

1.1 场地工程地质与水文地质条件

该项目建设场地为剥蚀残山地貌，场地内边坡与基坑开挖影响范围内的地基土，主要可以分为素填土、凝灰熔岩残积粘性土、全风化凝灰熔岩、砂土状强风化凝灰熔岩、碎块状强风化凝灰熔岩、中风化凝灰熔岩等6层岩土层。其中，基坑与边坡开挖过程中，侧壁出露的土层主要为全风化凝灰熔岩层。场地内各岩土层的主要计算参数如表1所示。

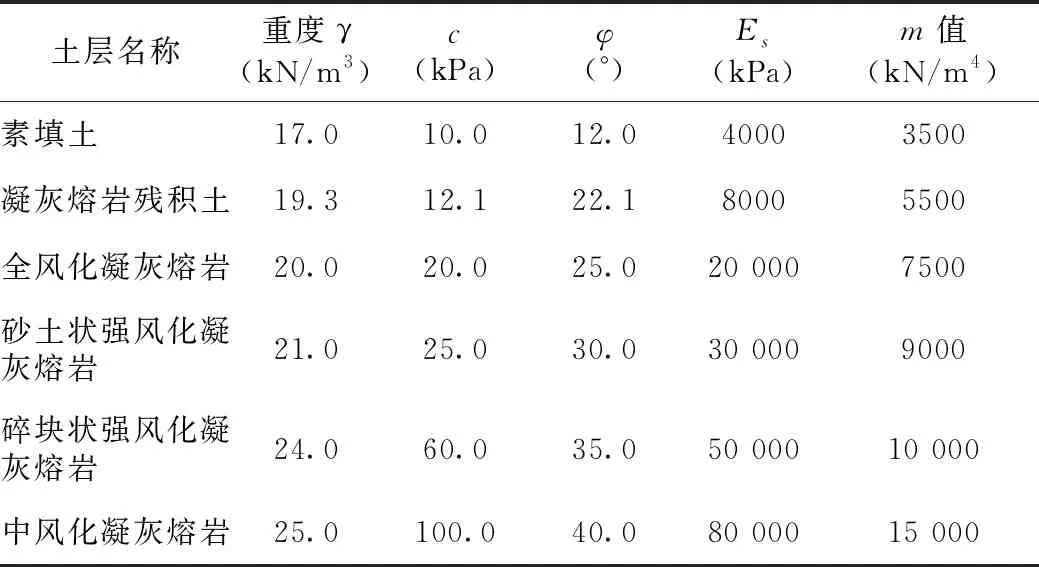
表1 场地主要地层计算参数表

场地内地下水主要为赋存于残积土层、全风化岩层与强风化岩层中的孔隙-裂隙型潜水。上述土层均为弱透水性土层，富水量差，场地地下水对边坡与基坑开挖影响较小。

1.2 边坡与基坑支护方案

该项目东侧位置上部永久性边坡高度为6.6 m，下部临时性基坑深度为9.4 m，边坡坡顶紧邻已有民房。为保证边坡与基坑开挖期间民房的安全性，边坡与基坑采用外锚式h形双排桩支护。考虑到边坡支护桩紧邻已有民房，为最大限度减少支护桩施工对邻近建筑物的影响，边坡支护桩采用人工挖孔桩，支护桩规格φ800@1300 mm，桩长13 m，排桩顶采用1.3 m×0.8 m冠梁连成整体，设两道不可拆除的永久性预应力锚索；基坑支护桩采用旋挖成孔灌注工艺，支护桩规格φ800@1300 mm，桩长13.0 m，排桩顶采用1.2 m×0.7 m冠梁连成整体设三道永久性预应力锚索，除第三道锚索水平间距为1.3 m外，其余各道锚索水平间距均为2.6 m。前后排支护桩在永久性边坡坡脚位置设置一道钢筋混凝土连系梁，连系梁截面为0.7 m×0.7 m，水平间距2.6 m，以上支护结构总体形成h形椅式双排桩结构。边坡与基坑支护结构剖面图如图1所示，双排桩及连系梁平面布置如图2所示。

图2 h形双排桩支护桩与连系梁平面布置

2 h形双排桩结构计算模型的建立

2.1 计算模型的确定

对于h形双排桩支护结构，抑或是长短桩组合的双排桩支护结构，现行国家规范尚未给出明确的计算模型与方法，目前市场上的商业设计软件也无法计算该型式的支护结构。对于h形双排桩，许多设计人员采用的简化计算方法是忽略连系梁的作用，将前后排支护桩分开计算结构内力与变形。对前排桩而言，该方法将前排桩桩顶以上的土体重量等效为地面超载，采用弹性支点法计算单排桩的内力与位移，这种简化方法从原理与计算模型上并没有存在太大问题。应当注意的问题仅仅是前排桩的桩顶附近位置由于受到连系梁约束作用，实际受到的弯矩值大于简化模型的弯矩计算值。然而对后排桩而言，单排桩弹性支点法的计算模型在前排桩被动侧土方未开挖时是适用的；但在前排桩被动侧土方开挖后，后排桩被动区土体不再符合半无限平面的假定，对后排桩的约束作用机理改变，此时单排桩弹性支点法计算模型不再适用。此外，分离式计算模型无法准确分析连系梁对前、后排支护桩变形和内力产生的影响，故而采用传统分离式排桩计算模型得到的计算结果存在一定缺陷。

本文参照行业标准《建筑基坑支护技术规程》4.1节与4.12节[8]中对弹性支点与双排桩支护结构的计算模型规定，采用平面杆系弹性支点法原理对h形双排桩支护结构内力与变形进行整体计算。排桩后方主动侧土体产生水平土压力荷载作用于支护桩桩身，土压力按朗肯土压力理论进行计算。前后排支护桩与连系梁简化为竖向放置于地基之上的弹性梁单元，预应力锚索简化为水平向弹性支座。基坑开挖面以下土体提供的反作用力简化为弹簧单元，弹簧的水平反力系数与分布土反力分别按式(1)与式(2)计算。

ks=m(z-h)

(1)

ps=ksv+ps0

(2)

位于前后排支护桩之间的土体按薄压缩层理论简化为拉结于双排桩杆件上的弹簧单元，桩间土弹簧单元刚度系数与桩间土对桩侧压力分别按式(3)与式(4)计算。

kc=Es/(sy-d)

(3)

pc=kcΔv+pc0

(4)

在弹性支点法模型中，预应力锚索作为支护桩弹性支座，其刚度系数按式(5)与式(6)计算。

(5)

(6)

由于连系梁与后排支护桩之间连接构造原因，连系梁上下侧仅有少量纵向钢筋植入后排桩中，其植筋长度难以满足传递平面弯矩要求，故连系梁与后排桩连接点按铰接计算；而与前排桩顶部通过冠梁连接，其纵向受力钢筋的锚固长度均能满足传递弯矩要求，故连系梁与前排桩连接点按刚接计算。本文计算所采用的h形双排桩支护结构的计算模型如图3所示。

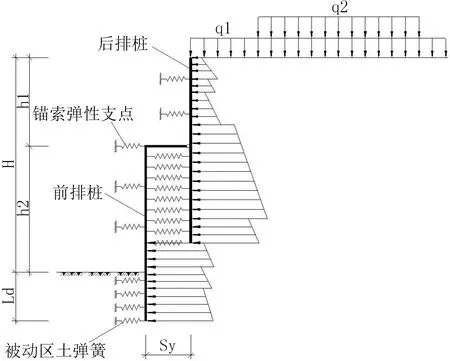
图3 h形双排桩支护结构计算模型

2.2 结构分析计算参数的选取

根据前文确定的计算模型，本文基于大型通用有限元分析软件ANSYS采用荷载-结构法对h形双排桩支护结构进行计算。结构计算中，前后排桩与连系梁采用三维线性有限应变梁beam188单元模拟，土体弹簧则采用轴向弹簧-阻尼器combin14单元模拟，各弹簧弹性系数依据前文所述方法计算确定，根据土体材料无法受拉的特性，弹簧单元在计算过程中不能出现受拉状态，否则应判定为无效弹簧。表2为排桩与连系梁单元的计算参数表，锚索弹簧单元的设计参数与支锚刚度值如表3所示。计算模型中水平土压力采用朗肯主动土压力理论计算，计算土压力所采用的土层抗剪强度指标如表1所示。

表2 结构构件有限元计算参数

表3 预应力锚索参数表

2.3 计算工况的设定

考虑到项目总体施工顺序及周边环境保护要求，该项目边坡与基坑采用自上而下逆作方式施工，即在边坡支护桩施工完成后，自边坡坡顶标高逐步向下开挖，锁定一道锚索，开挖一层土方；开挖至永久性边坡坡脚标高后，施工基坑支护桩，并施工混凝土连系梁连接前后排支护桩，而后逐层向下开挖，同样采用锁定一道锚索开挖一层土方的方式，直至开挖至基底设计标高。根据上述施工方式，支护结构计算中共分6个施工工况，如表4所示。

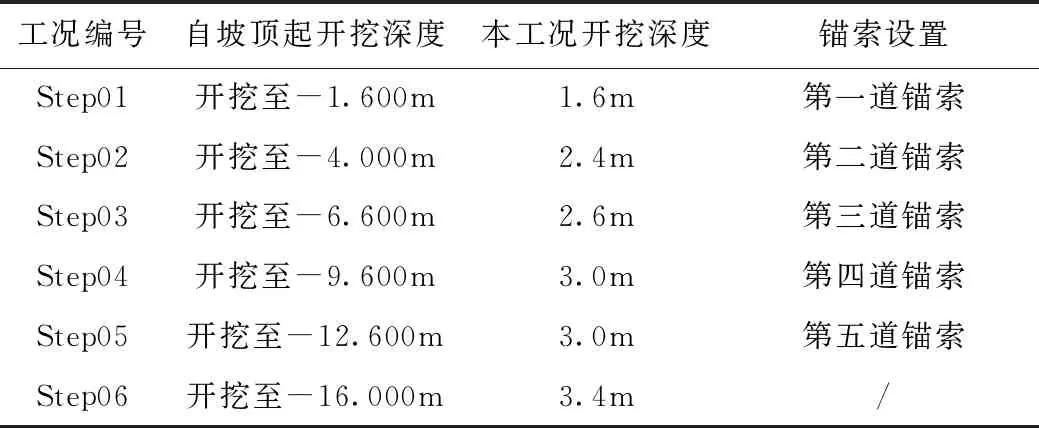
表4 开挖施工工况设定表

3 支护结构计算结果分析

3.1 分离式简化模型计算结果分析

采用前、后排桩分离的简化计算模型时，因该模型无法分析后排桩在基坑开挖之后内力与变形，为与后文中整体模型计算结果对比，本次以前排桩计算结果进行两种计算模型的对比分析。采用分离式简化模型计算得到前排桩的变形和弯矩图分别如图4～图5所示。从图中可以看出，采用分离式简化模型计算得到的前排桩桩身最大变形约为34.40 mm，桩身最大弯矩值约为793.07 kN·m，设置于基坑支护桩前的三道锚索轴向拉力标准值自上而下分别为198.20 kN、145.09 kN、147.62 kN。

图4 简化模型前排桩各工况下水平位移曲线

图5 简化模型前排桩各工况下弯矩图

3.2 整体式模型计算结果分析

经计算，采用整体模型计算得到的前排桩与后排桩在各开挖工况下水平位移分别如图6～图7所示。

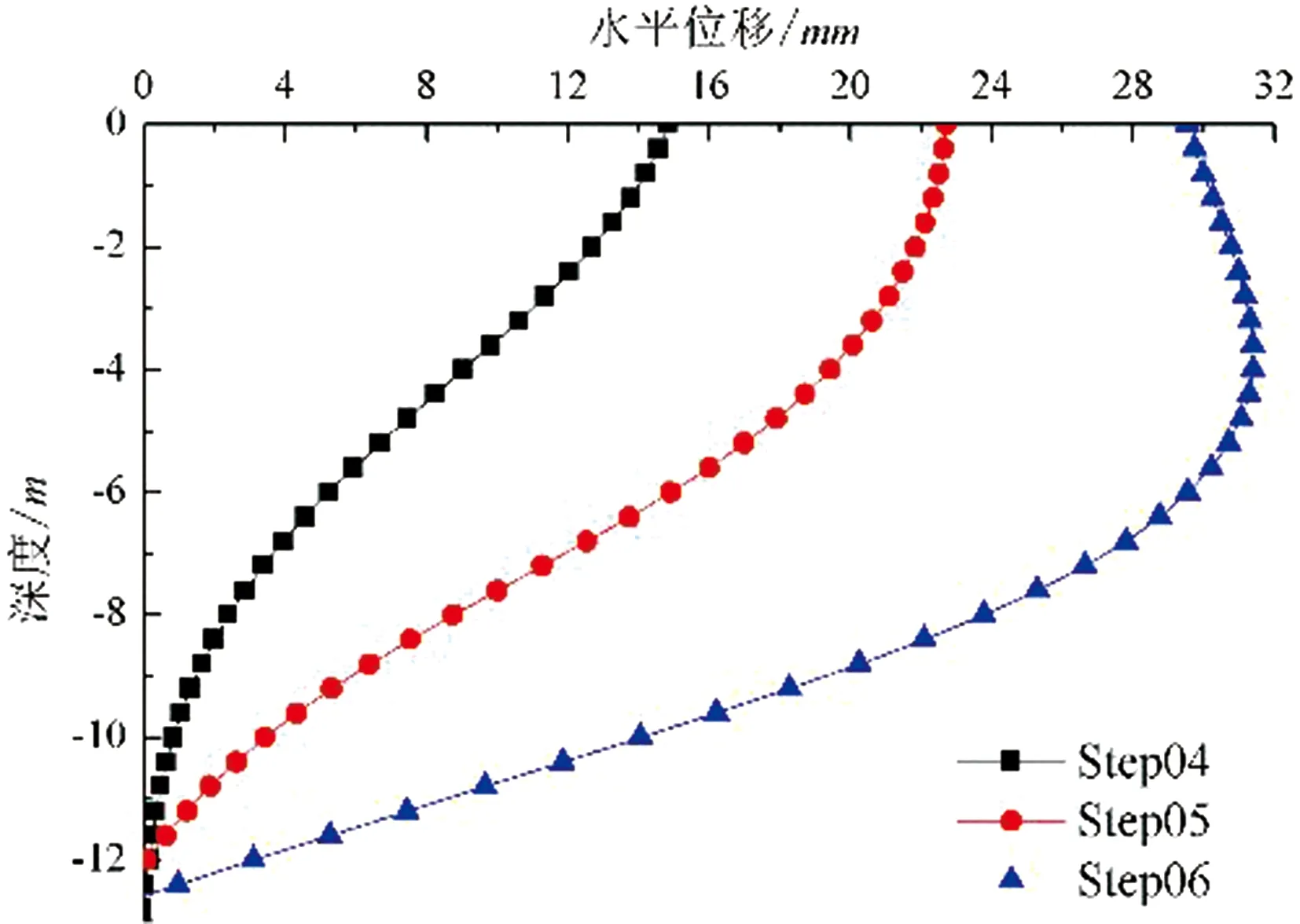
图6 整体模型前排桩各工况下水平位移曲线

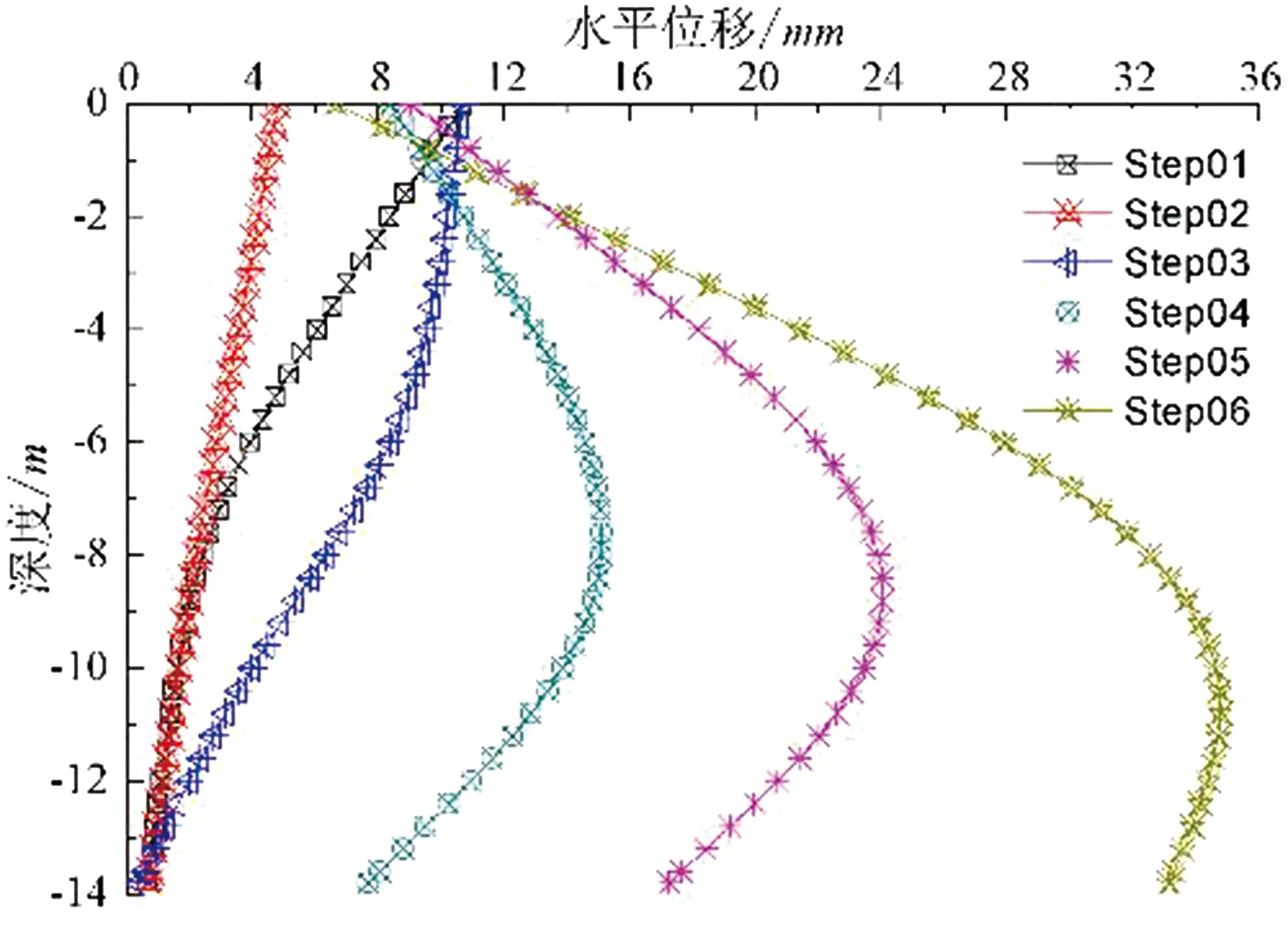
图7 整体模型后排桩各工况下水平位移曲线

分析支护桩变形计算结果可知，随着边坡与基坑被动侧土方开挖，支护桩水平变形逐渐增大。位于前排基坑支护桩的变形曲线呈典型外锚式排桩的变形特征，桩顶变形受到第三道锚索与连系梁约束作用，变形略小于深部位置，这种变形模式随着开挖深度增大越发明显，桩身最大变形位置深度约为10.4 m，最大变形约为31.39 mm。位于后排边坡支护桩变形规律则分为两个阶段，第一阶段为前排桩被动侧土方开挖之前，支护桩变形曲线亦呈现出外锚式单排桩的变形模式；随着前排桩被动侧土方逐步开挖，后排桩逐渐呈现出“踢脚型”变形规律，产生最大变形位置位于后排桩桩底至连系梁之间，最大变形约为34.79 mm。

对比后排桩嵌固深度范围内前、后排桩桩身位移可以发现，该范围内后排桩桩身水平位移大于前排桩桩身位移，说明双排桩之间土层发生压缩变形，用于模拟桩间土体的弹簧单元没有出现受拉状态，符合计算模型中桩间土的薄压缩层假定。桩间土受到后排桩的推力，产生压缩，同时将压力传导至前排支护桩，使前排桩产生变形。

图8与图9分别为前排桩与后排桩在各开挖工况下桩身弯矩图，根据弹性支点法计算结果，在工况Step06，各道锚索受到轴向拉力标准值自上而下分别为57.24 kN、106.61 kN、265.01 kN、174.98 kN、220.23 kN。从图中可以看出，前排基坑支护桩在桩顶位置明显受到连系梁转角变形约束作用，桩顶弯矩不再为零；随着基坑被动侧土方开挖，桩身弯矩逐步增大，最大弯矩位置略高于基坑开挖面，至开挖到基底时，桩身最大弯矩标准值约为685.57 kN·m。后排边坡支护桩桩身弯矩随着桩前土方开挖深度增加而逐步增大，在基坑内土方尚未开挖时(工况Step01～Step03)，桩身最大弯矩值变化较小，约为146.56 kN·m；而在基坑内土方开挖后(工况Step04～Step06)，由于支护桩发生“踢脚状”变形，桩身弯曲变形曲率增加，弯矩值急剧增大，至开挖到基底时，桩身最大弯矩约为395.82 kN·m。

图8 整体模型前排桩各工况下桩身弯矩图

图9 整体模型后排桩各工况下桩身弯矩图

图10 整体模型连系梁各工况下弯矩图

图10为h形双排桩连系梁在各开挖工况下的弯矩图，在所有工况中，连梁受到最大弯矩为297.85 kN·m。基坑开挖后各工况中(Step04～Step06)，连系梁轴力值分别为-140.56 kN、-100.27 kN、-67.13 kN，连系梁始终处于受压状态，其受到的剪力值分别为88.91 kN、29.43 kN、61.89 kN。

对比两种计算模型计算结果可以看出，前排桩被动侧土方开挖后，后排桩桩身变形与弯矩值持续增大，出现“踢脚”变形现象，而采用简化计算模型却无法正确计算这种工况。就前排桩的计算结果而言，采用整体式计算模型时，由于连系梁对前排桩转角约束作用，支护桩顶的弯矩不再为零，受此影响，支护桩下部位置桩身弯矩最大值较简化模型计算结果略有减少，两种计算模型计算得到的桩身最大变形则较为接近。

对比两种模型计算得到的锚索轴力标准值，可以发现，对设置在基坑支护桩上的锚索而言，简化模型计算得到的锚索轴力小于整体模型计算得到的锚索轴力。分析这一现象，其原因在于后排桩受主动土压力作用向基坑开挖方向变形后，双排桩之间土体受挤压对前排桩产生侧向压力，该侧向压力值大于简化模型计算中采用的朗肯主动土压力理论值，进而使整体模型计算中得到的锚索轴向拉力标准值增大。这一点从各工况中连系梁始终处于受压状态也可以间接反映出来。

4 结论

本文以某边坡与基坑联合支护实际工程为算例，研究了长短桩组合的h形双排桩支护结构内力与变形的计算模型，同时对应用于工程中的分离式简化计算模型与整体计算模型的计算结果进行对比分析。通过ANSYS有限元分析软件对弹性支点杆系结构的分析，得出如下结论：

(1)结合规范中的弹性支点法提出了h形双排桩支护结构的计算模型，计算模型能够对前排桩、后排桩、连系梁及锚索等构件进行整体计算分析，精确得出支护结构在各开挖工况下的内力与变形。

(2)当采用简化模型计算支护结构内力与变形时，对后排桩其计算得到的内力与变形偏小，且无法准确计算前排桩前土方开挖后支护结构的内力与变形；对前排桩其计算得到的最大内力与变形与整体式模型相接近，能满足工程应用要求。

(3)当采用分离式简化模型进行支护结构计算时，鉴于其计算结果的误差，应在实际进行排桩配筋计算时进行调整。对于后排桩，适当加强嵌固段配筋，对于前排桩，适当加强桩顶附近位置配筋。