高速铁路滚子轴承中凸度滚子接触参数分析与轴承稳健设计模型
2021-07-04杨咸启时大方刘国仓
杨咸启,时大方,刘国仓
(1.安徽建筑大学 城市建设学院,安徽 合肥238076;2.浙江天马轴承集团有限公司,浙江 湖州313200;3.黄山学院,安徽 黄山245041)
1 线接触问题概述
在高速铁路轴承和重载轧机轴承等一类滚子轴承中,多是采用圆柱滚子轴承或是圆锥滚子轴承,其中的接触问题主要属于线接触类型。由于滚子和滚道接触都是具有限长度的,不符合理想的线接触类型问题的条件,只能通过数值计算方法计算。随着载荷的增加,有限长线接触区域会逐渐扩大[1-3]。当载荷比较大时,在接触区两端部边界会出现很高的应力集中问题,如图1(a)所示。为了消除这种不利的应力集中现象,滚子的母线需要采取修形设计。早先的修形母线通常采用小角度倾斜直线或圆弧曲线,等等。经过这样修形后的滚子能够降低接触应力集中度,但不能完全避免应力集中,如图1(b)所示。如果滚子母线采用圆弧曲线,可以避免滚子边缘应力集中,如图1(c)所示。但这时接触中心区的接触应力会比较高,它会减少轴承接触疲劳寿命。经过不断深入的研究发现,如果滚子母线采用对数型曲线,理论上可以完全消除应力集中现象,可以使接触压力分布接近均匀,如图1(d)所示。因此,在重要的滚子轴承设计中都推荐采用对数型曲线来作为滚子的母线。设计中通常的做法有两种:1.滚子母线直接采用对称型的对数曲线;2.在滚子母线中段采用一段直线,在滚子两端部采用对数曲线,使两者光滑连接。这样接触应力就能够比较均匀分布。

图1 不同的母线滚子接触压力分布情况
滚子母线经过修形后,接触应力和接触变形计算比较复杂,目前还没有理论计算公式可直接应用。有条件的情况下可以采用商业分析软件来计算,但这些软件所采用的计算模型需要事先确定,给计算带来不便。本文针对不同的滚子母线曲线,讨论它们的接触应力特点,提出采用线条元模型的计算方法。由于母线修形主要在滚子端部,因此,在滚子中部可采用理想线接触计算方法,而在滚子端部则采用简化的计算方法。当计算出表面的接触压力后可以进一步计算接触体内部材料的应力[2-7],从而为轴承的接触疲劳分析及其他特性计算服务,为轴承设计带来方便。经过接触力学参数分析之后,提出了高速和重载铁路滚子轴承优化稳健设计思想和方法,丰富了轴承设计理论。
2 理想线接触压力计算模型
设两个光滑的弹性圆柱体长度同为l,其轴线平行,在外力Q作用下对中接触,这就是一种理想的线接触模型,如图2(a)所示。
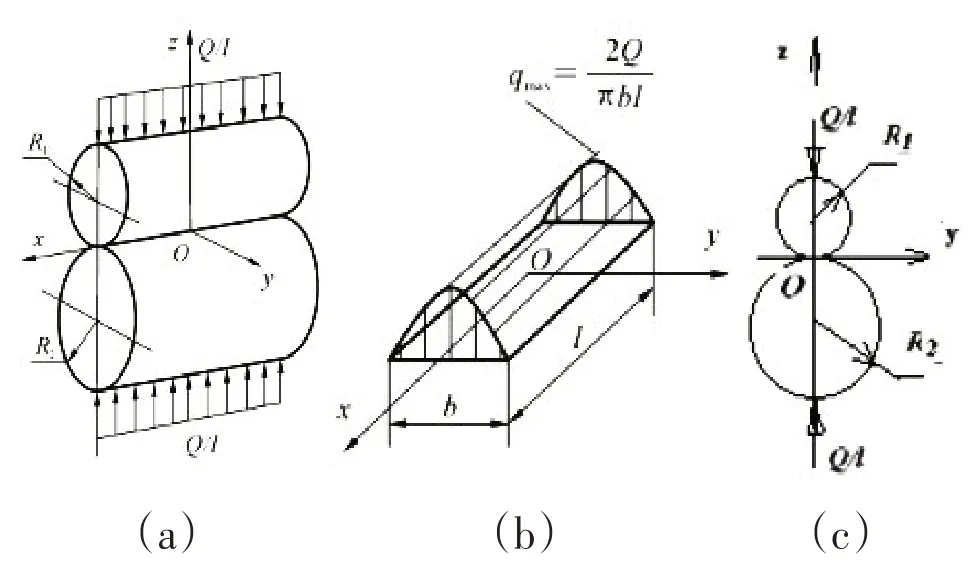
图2 两个长度相同圆柱体理想线接触模型
由赫兹接触理论知道,对点接触模型,首先假设接触区形状为椭圆形状,再假定接触压力分布为与椭圆形区域相适应的椭球形分布,最后利用接触表面几何方程和接触变形协调条件,确定出接触区的大小和压力分布函数。对于理想的线接触模型,同样也采用假设接触区域为矩形,沿滚子轴线的接触压力为均匀分布,沿周向的压力分布为椭圆曲线,即为椭圆柱形状,如图2(b)所示的接触区域及接触压力放大图。这样,理想线接触问题可以转化为平面接触问题,如图2(c)所示。对无限长线接触问题,它可转化为平面应变问题(εx=0),对等长度线接触它可转化为平面应力问题(σx=0)。但线接触问题与点接触问题不同,在弹性力学理论上,它存在接触变形不能确定的问题。
在文献[7]中,介绍了理想线接触模型的理论计算公式。在理想线接触条件下,假设接触压力分布函数为:

式中,qmax为接触表面的最大压力,b为接触区半宽度。
由外力与接触力的平衡条件,并且利用半椭圆柱体的体积积分得到

因此,得到接触表面的最大压力为

为了求出接触表面上的变形,当已知压力的分布函数后,由波西涅斯克解[7],接触表面的变形可以表示为

式中,E为弹性模量,ν为泊松比,代表矩形接触区域。
利用变量积分变换方法,上式中的积分变换为

进一步,如果两个接触圆柱体的半径分别为R1、R2,其材料弹性模量和泊松比分别为E1、ν1;E2、ν2。利用接触表面的几何关系和变形协调条件,可以导出接触区域半宽度和最大接触压力的计算公式。根据平面接触的特点,假设开始接触点的切平面保持不变,接触变形发生应该满足下面的接触变形的协调条件。

上式中,δ(0)代表初始接触点上两个圆柱体的变形和(也称为两者的弹性变形趋近量)。
在上面的方程中,两个柱面之间的距离近似为

这样,接触变形的协调条件(5)可以改写为

如果采用两个圆柱体的参数来简化表示时,可令

方程(6)是一种广义积分方程,不容易直接求解。但上述方程是包含变量y的函数关系式,将方程(6)对y求导数,得

对上式积分得

比较上方程变量的系数得到

将接触压力公式(2)代入上式,得接触区域半宽度为
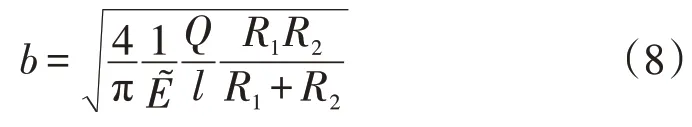
利用方程(6),进一步将两个圆柱体的接触中心趋近量化简为

上式对于坐标y的任意值都应该成立。特别当y=0时,必须满足

式中的J(0)还不能直接求出。
为了解决这一问题,通常采用近似的计算方法。例如K.L.Johson利用平面应变状态积分,导出两个圆柱体接触区中心弹性趋近量近似公式为

式中,Q为作用外力,l为接触圆柱体长度,R1、R2分别为接触圆柱体的半径,b为接触区域半宽度,E1、ν1;E2、ν2分别为材料弹性模量和泊松比。
G.Lundberg与H.Sjovall针对轴承中的理想线接触区中心弹性趋近量近似公式为

式中,Q为接触区作用外力,l为接触圆柱体长度,E、ν分别为轴承材料弹性模量和泊松比。为轴承内外圈与滚动体接触结构参数。
而A.Palmgren通过试验给出带凸度的圆柱体接触中心弹性趋近量的近似公式为

式中,Q为作用外载荷(N),l为接触圆柱体长度(mm),͂为当量弹性模量(MPa)。
对于平面应变状态下,接触表面下,沿对称轴上的主应力为

因此,在对称轴上的最大剪应力为

具体计算得出,当z=0.786b,τmax(x=0)=0.301qmax。当z=0.165b,τmax(x=0)=0.262qmax。
对于平面应力状态下的应力,如两个圆盘接触,表面下沿对称轴上的主应力计算时,将上面的平面应变状态主应力公式中的泊松系数ν换成ν/(1+ν)即可。
3 有限长线接触压力的有限条元分析方法
有限长线接触如图3(a)所示。Harris等人已经介绍了典型的有限长线接触的计算例子,计算结果如图3(b)、(c)所示[2,3]。从图中可以看出,有限长线接触的接触压力分布,在圆柱的端部出现了明显的应力集中。接触区域的形状也不再是严格的矩形形状。
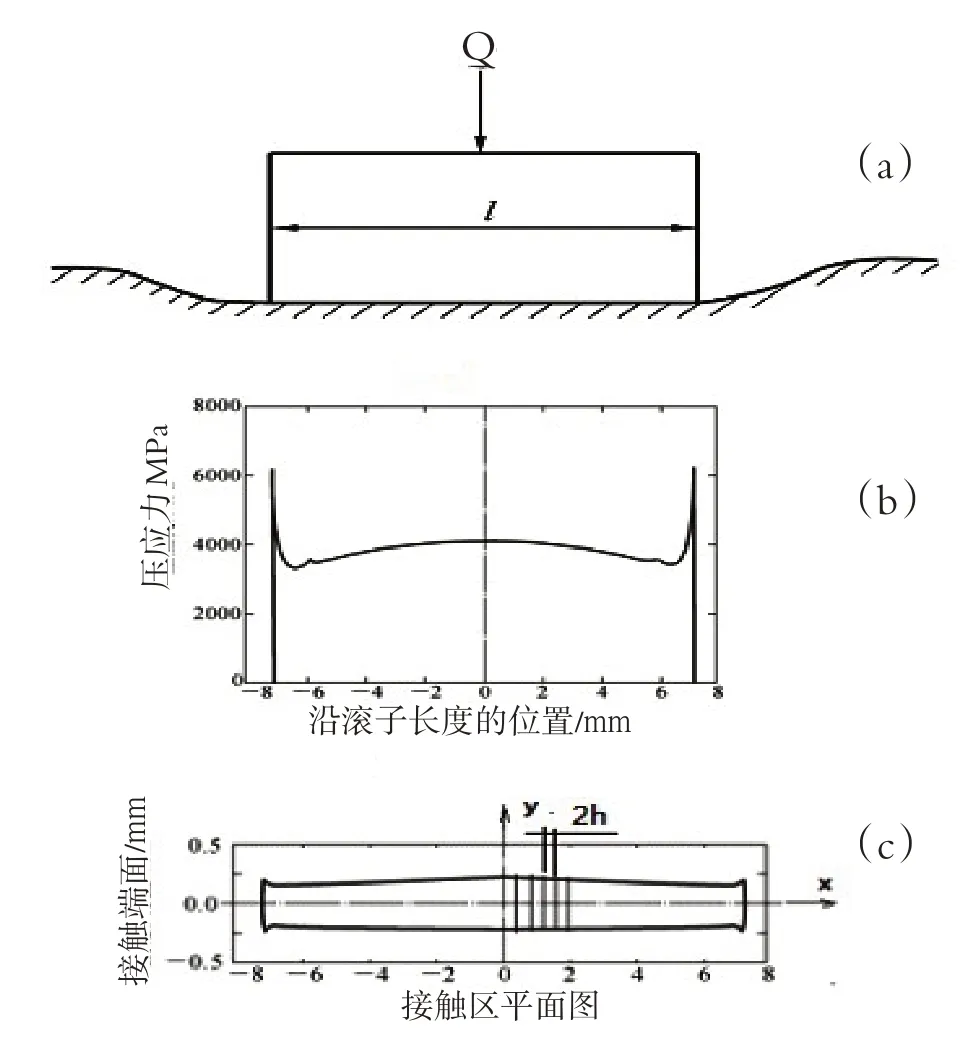
图3 典型有限长线接触结果
对于接触问题求解,需要满足的第一个要求是接触力平衡条件,即在接触区上的全部接触压力合力与外载荷平衡,设接触区的分布压力为q(x,y),载荷平衡关系可以表示为:

接触问题求解需要满足的第二个要求是两个物体接触变形满足协调条件,即

其中,δ(0)为接触体1与2的接触区中心的变形之和,w1(x,y),w2(x,y)为接触体1与2的接触表面上各点的变形,z1(x,y),z2(x,y)为接触体1与2的接触表面形状各点的坐标。
又根据表面接触变形位移的计算方法(波西涅斯克模型)[7],接触表面上各点的变形大小为:
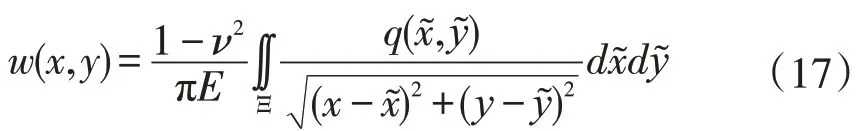
方程(15)-(17)是接触问题求解的基本方程,目前还没有理论解,多采用数值方法求解。先设定可能的接触区域,并划分为一系列的微小矩形单元面(如图4),在每个小的单元面上假定接触压力为常值(未知量),利用接触压力平衡条件(15)和接触变形协调条件(16),建立求解方程[4]。但这样做求解的未知量比较多,需要迭代次数多,计算费时。

图4 接触区域划分
如果针对线接触压力分布和接触区域的特点,将接触区域沿长度x方向划分为微小单元条nij,长度与宽度为2h×2b,如图3(c)中的线条分割所示的条状区域。在每个微小单元条接触区域上,我们假设接触压力分布函数为(见图5):

图5 接触压力分布函数模型

式中,q m(x)为x轴上最大接触压力,B(x,y)为有限条上压力变化的分布函数。
根据不同的接触压力分布模型,B(x,y)可以取不同的函数形式来插值模拟接触压力变化。本文进一步假设沿y方向压力的变化为椭圆函数,则B(x,y)可以取为:
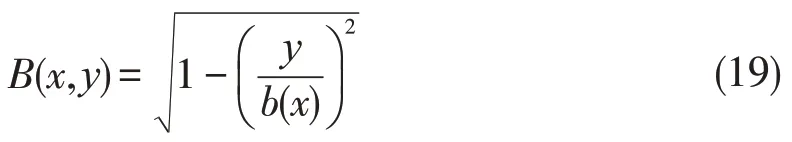
式中,b(x)为接触区半宽度。
下面再建立数值计算方法。在微小单元条接触区域nij中心点(xij,y ij)上,接触变形的计算公式(17)中的积分可表示为:

将式(20)带入到两个物体接触变形协调条件(16)后,可以得到

式中,ij=1,2,3,…,MN,MN为x坐标轴方向上数值计算点总数量,δ0=δ(0)。
式(21)是有MN个方程的方程组,其中的未知量为q m有MN个,及δ0共有MN+1个。这样不能直接求解,需要再增加接触压力平衡方程(15)。
在接触压力为半椭圆分布假设下,接触平衡条件(15)的积分表示为:
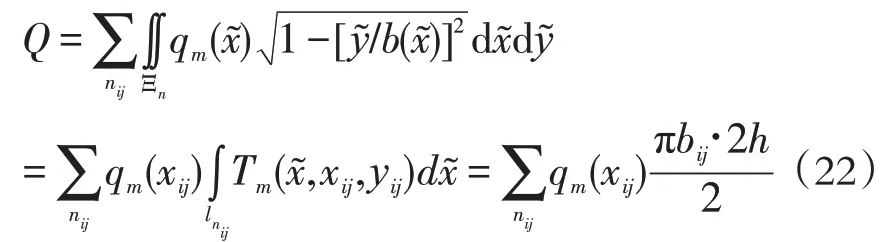
这样,联立式(21)、(22)为1组方程组。求解这些方程组可以得到接触区域上的压力分布qm和δ0。在整个求解过程中,由于接触区大小在计算之前是未知的,必须首先假定接触区域形状大小进行试计算,计算中必须保证接触压力为非负值(q m≥0)。通过不断迭代修正接触区,最后确定出符合实际的接触区的形状和接触压力的分布。
4 轴承中的有限长线接触参数的工程计算方法
在滚子轴承工程设计计算中,当计算接触压力时,需要确定接触区半宽度b,它与线接触滚子的母线形状有关。下面针对几种滚子母线形状函数,讨论接触区参数的工程计算方法。
设圆柱滚子的总长度为lw;初始接触点的直径为Dw,作用接触载荷为QW,有效接触区长度为le,一对接触圆柱体的半径分别为R1、R2。
4.1 对数曲线型母线滚子
在对数母线滚子的设计中,为了使滚子母线为光滑完整的对数曲线,同时也与滚子的凸度相对应,对数曲线通常要根据滚子的凸度值来设计,而凸度设计值可以由滚子最大的受载接触变形来确定。一般采用的光滑完整的对称型母线的对数曲线函数为:

式中,ε0为滚子凸度值,α、β为系数。当x=0时,z=0;当x=l e/2时,z=ε0。利用这些条件可以确定函数中的系数α、β的值。
有时为了滚子母线加工方便,只在滚子的端部区域采用对数曲线修形,而在滚子中部仍然采用直线。这时的滚子母线函数形式为:

其中,l0为滚子直母线段长度,ζ、η为系数。当x=l0/2时,z=0;当x=l e/2时,z=ε0。利用这些条件同样可以确定函数中的系数ζ、η的值。当式(20)中的l0=0,它与式(23)相似。对数曲线型母线滚子剖面如图6所示。
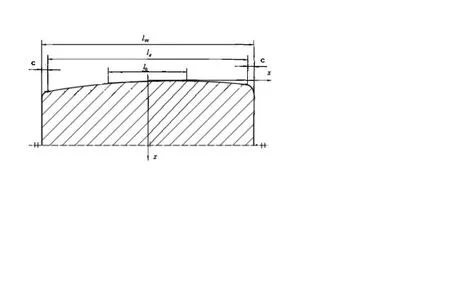
图6 对数母线滚子剖面图
对于上面两种形式的对数曲线滚子,接触区的宽度和接触压力的计算方法可统一如下。
在保证满足外力与接触压力符合平衡方程(15)的前提条件下,将载荷QW分为两部分,一部分由滚子直线段承担,一部分由滚子端部曲线段承担。若QW比较小,接触区不超出滚子有效接触长度时,QW全部由直母线部分承担,可采用理想线接触参数计算方法(公式(1)-(3))。而当QW比较大时,整个对数曲线母线部分的接触参数计算方法如下:

其中,Q C为滚子直线段承担的载荷,Q E为对数曲线段承担的载荷,Q W=Q C+Q E。aE、bE分别为滚子直线段端点处的接触椭圆长、短半轴尺寸。Σρ(x)=2/D w+z″(x)±ρi,e,z″(x)为滚子母线的接触点处的曲率,ρi,e为内圈(或外圈)接触点处的周向曲率,,d m为轴承节圆直径,α为轴承接触角。符号“-”对应内圈,“+”对应外圈。
当载荷QW很大,接触区长度已经超出滚子有效接触长度时,接触区成为完整的线接触模型,可采用线接触公式计算如下:
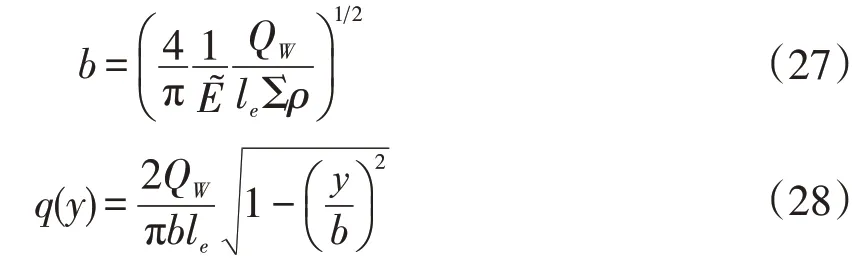
4.2 圆弧倒角曲线型母线滚子
当滚子母线采用对称型部分圆弧修型母线,圆弧曲线与直线光滑连接,则滚子的母线函数为:
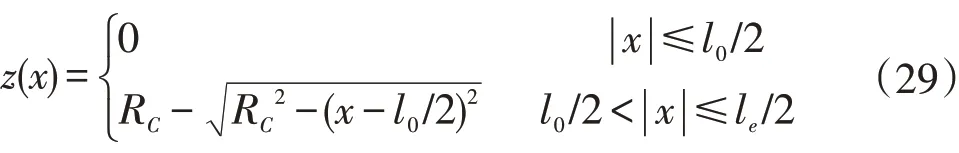
其中,l0为滚子直母线长度值,圆弧半径R C=[(l w-2c)2-(l w-2t)2]/(8ε0),l w为滚子全长,c为滚子端面倒角尺寸,t为凸度修正圆弧部分长度,ε0为滚子凸度值。滚子母线剖面如图7所示。

图7 滚子部分圆弧修型母线剖面图
这时,接触区的宽度和接触压力的计算方法也需 要 按 照 式(26)-(28)计 算,此 时 取Σρ=2/D w+1/R C±ρi,e。
4.3 倾斜直线倒角修型母线滚子
如果滚子母线采用对称型倾斜直线倒角修型母线,则滚子的母线函数为:

其中,l0为滚子直母线长度值,θ为斜直线倾角。滚子母线剖面如图8所示。

图8 滚子倾斜直线修型母线剖面图
这种母线不常采用,它的接触区的宽度和接触压力可采用线接触公式(1)-(3)近似计算[2.3]。
4.4 大圆弧曲线型母线滚子
如果滚子母线采用对称完整大圆弧曲线母时,则滚子的母线函数为:
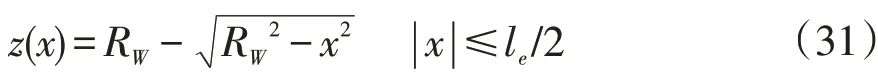
其中,RW为滚子直母线弧的半径值。滚子母线剖面如图9所示。
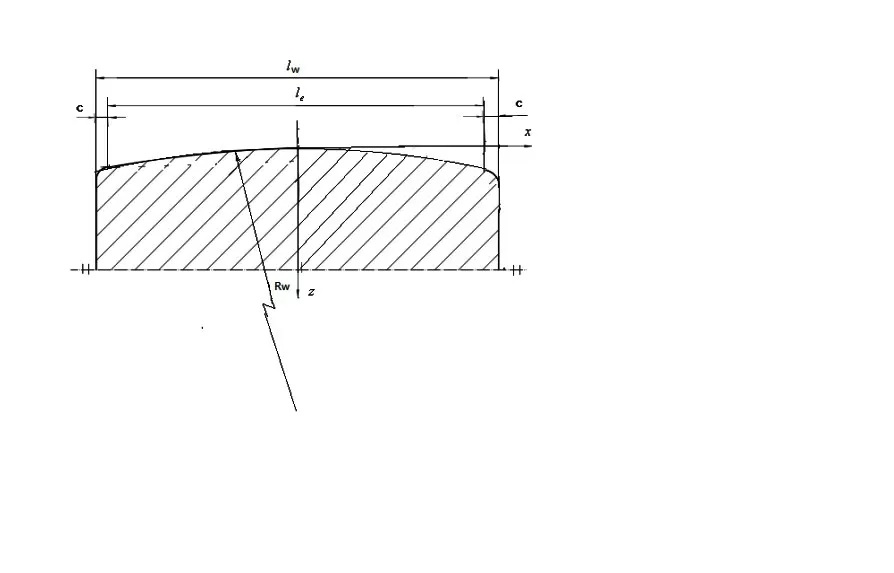
图9 大圆弧滚子数母线剖面
此时接触区为椭圆,椭圆尺寸大小和接触参数按照点接触公式计算如下[2,7]:

上面各式中,取Σρ=2/D w+1/R w±ρi,e,a*,b*为赫兹接触计算系数。
如果随着载荷的增加,出现椭圆长轴值超出滚子有效接触区长度,这时需要对点接触结果进行适当修正[8]。
5 轴承滚道接触力学参数化设计的数学模型
对于一般的圆锥滚子轴承,滚道接触参数a、b、δ、qmax与轴承接触点处的曲率、接触载荷以及材料力学性能常数等有关。因此,对整个轴承来说,可以建立下面一种泛函关系式:
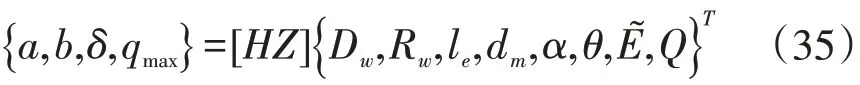
式中,左边的量为圆锥轴承滚道接触参数,右边是与轴承接触点处的结构参数、材料常数、接触载荷等。[HZ]是一种矩阵泛函关系。
当对一些轴承滚道接触参数作出某些要求(或限制)时,可以对结构参数进行规划设计。这是一种接触力学参数设计思想。采用数学方法表达时,可以写成
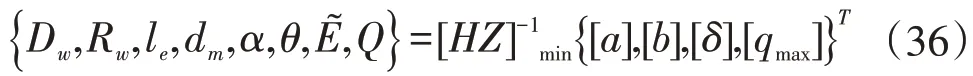
其中[a],[b],[δ],[qmax]表示对接触区域尺寸、接触变形和最大接触压力等参数的限制性要求值。它们可以根据需要来挑选。
[HZ]-1min表示泛函矩阵逆向优化运算,这一过程可以利用程序在计算机上完成。
对于其他类型的滚子轴承,也可以建立类似的设计模型。对于球轴承,滚道接触参数a、b、δ、qmax与轴承接触点处的曲率、接触载荷以及材料力学性能常数等有关。因此,对整个轴承来说,可以建立下面一种泛函关系式

式中,左边的量为深沟球轴承滚道接触参数,右边是与轴承接触点处的结构参数、材料常数、接触载荷等。[HZ]是一种轴承接触参数计算过程的矩阵泛函关系。
当对轴承接触参数作出某些要求(或限制)时,则可以对轴承滚道结构参数进行规划设计。这是一种接触力学参数化设计思想。采用数学方法表达时可以写成

其中[a],[δ],[qmax]表示对接触区长轴尺寸、变形和最大接触压力等参数的限制性要求值,它们可以根据情况来挑选。
[HZ]-1min表示泛函矩阵逆向优化运算。根据接触力学中的计算公式和稳健优化原理进行分析,这一过程可以利用程序在计算机上完成。
对接触参数的限制性要求取值,应该根据不同的使用场合,选择不同的限制值。例如,对通用轴承,限制值可以选择稳健的可靠性高的值,对应的设计称为稳健的可靠性设计;而对于特殊使用的专用轴承,限制值可以选择极限值,对应的设计称为极限设计[8]。
6 结论
本文讨论了滚子轴承中凸度滚子有限长线接触问题的计算方法,主要的结果如下:
1.在有限长线接触数值计算方法中,建立了有限条元分析模型。与传统的数值计算方法相比,它可以有效地简化计算过程,提高计算效率。
2.针对滚子轴承设计中不同的凸度滚子母线,提出了接触区形状和接触压力的工程计算方法。它与商业软件系统中的模型方法计算结果对比,本文方法与软件方法得到的接触参数计算结果接近。
3.建立轴承接触参数的稳健优化设计的模型理论,为提高轴承的可靠性使用性能提供了方法。
