聚焦新旧知识 有效备战中考——以初三阶段的数学复习教学为例

湖南省长沙市南雅中学 吴宏波

复习课是初三阶段的重点，为了帮助学生有效备战中考，教师应基于课程标准和学生的基本需求优化复习教学策略，引导学生在自主知识建构中全面把握数学结构。同时，教师还应鼓励学生自主探索，使学生在新旧知识的衔接中强化复习效果。

一、明确复习计划，提高复习有序性

数学学科中所涉内容较多，为了提高复习的有序性，教师可以安排三轮复习，并明确每一轮复习的计划，以确保学生能够根据复习计划展开针对性的学习与练习，从而提高复习效果。

以“一元一次方程”这一单元的复习教学为例，首先，可以让学生以课本为指导进行复习，通过梳理知识脉络初步帮助学生建立逻辑思维能力。例如：

一元一次方程的定义：只含有一个未知数，未知数的次数都是1，等号两边都是整式。一般形式为ax+b=0。

一元一次方程的解法：需要考虑等式的基本性质和解方程的一般步骤。

等式性质1：如果a=b，那么a±c=b±c。

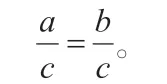
解方程一般步骤：去分母——去括号——移项——合并同类项——未知数的系数化为1。

这一环节，学生能够牢记基本的概念和性质，并掌握一定的解题方法和技巧，同时对知识形成系统化的认知。

其次，在构建基础知识结构后，可以着手从教学重点出发，实现学生的综合能力提升。可以借助经典例题展开专题复习，让学生对一元一次方程有更加深入的理解。例如：

（1）已知3 是关于x的方程2x-a=1 的解，则a的值是？

（2）已知（a-3）（2a+5）x+（a-3）y+6=0 是一元一次方程，求a的值。

以上问题既考查了学生对一元一次方程相关概念的理解，也考查了学生对一元一方程解法的掌握程度。对于学生掌握这一专题知识具有重要作用。

最后则是对学生考试习惯和应试技巧的培养，可以选择模拟训练的方式，让学生根据自身情况进行针对性的练习，利用试卷了解学生的考试情况和状态，安排层次性的训练题，并及时与学生进行心理沟通。

二、回归课本基础，进行知识建构

课本是基础，学生在解数学题时所应用到的理论和法则都与课本息息相关。所以，教师应给予学生充足的时间查漏补缺，在回归课本的过程中完成知识建构，从而更好地投入复习备考中。

以“不等式与不等式组”这一单元的复习教学为例，为了带领学生回归课本基础，且能够让学生在复习中自主进行查漏补缺，我要求学生在复习中画出思维导图，进行基本的知识建构，使学生对该单元知识有更全面的了解。

首先是知识要点归纳：基本概念、不等式的性质、规律与方法、不等式（组）在实际生活中的应用。

不等式的基本概念有：不等式、不等式的解、一元一次不等式、一元一次不等式组等。

不等式的性质包括：不等式两边加或减去同一个数或式子，不等号方向不变；不等式两边都乘或除以同一个正数，不等号方向不变；不等式的两边都乘或除以同一个负数，不等号方向改变。

不等式的规律与方法：分别掌握一元一次不等式和一元一次不等式组的解法。

不等式组在生活中的应用：学校购买了篮球和排球共100 只，篮球单价130 元，排球单价100 元，如果购买100 只球所花费用不少于11800 元，不超过11900 元，有哪些购买方案？

通过对以上知识要点的归纳，能够使学生全面掌握单元基础知识。其次是单元知识关系。

不等关系包含不等式、一元一次不等式、一元一次不等式组。

不等式包含不等式的性质。

一元一次不等式与一元不等式组都包含解法，解法中需要掌握解集和数轴的表示方法，并进行实际应用。

在回归课本基础的过程中，教师应给予学生充分的自由，促使学生在知识架构的基础上对该单元知识有全面的了解。在知识建构中，学生的数学应用能力也可以得到提升。

三、开展专项复习，提高复习针对性

很多学生在复习某一部分知识的过程中都存在复习效果不佳的问题，为了有效避免时间上的浪费，教师可以根据学生的复习情况组织专项复习，为学生提供针对性复习的机会，使学生的复习效果得到有效提升。

针对“用二次函数解决实际问题”这一重要考点，我开展了一场专项复习。在复习教学过程中，我对学生进行了分组，要求各小组学生先进行二次函数相关知识的总结，例如：二次函数的解析式（一般式、顶点式、两根式）；二次函数的性质；二次函数的图像与a、b、c符号的关系；二次函数与一元二次方程的关系等。之后，组织学生以小组为单位展开专项复习，为学生提供相应练习题，如下：

（1）某钢笔进价8 元一支，按10 元一支出售，每天能够卖出20 支，如果每支涨价1 元，就会少卖两支。为了获得最大利润，售价应定为多少？

（2）将一条长20 cm 的铁丝剪成两段，两段各围成一个正方形，则这两个正方形面积之和的最小值是多少？

让学生进行练习，并要求学生记录自己在解题中遇到的问题。

通过专项复习，学生对如何用二次函数解决实际问题有了更为深刻的认识，同时对不同类型的练习题进行了分析，从而理解了用函数知识解决最值问题的思路，这对于提高初中生的数学解题能力起到了重要作用。

四、增强训练强度，提高复习效率

复习教学离不开训练，备考所备的是学生对数学题的理解能力和解题能力。正所谓“熟能生巧”，只有增强训练强度，让学生在训练中完成对相关题型的复习和强化，才能真正提高复习效率，促使学生有效备战中考。

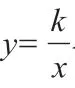
在带领学生进行了初步复习之后，我向大家分发了一份难度体现层次性的训练题，要求学生自主选择，并在完成某一难度习题的基础上朝更高层次冲击。内容如下：

基础难度：

已知y=（m-2）是反比例函数，则m的值是多少？

中等难度：

已知y=y1+y2，y1与x成正比例，y2与x成反比例，当x=-1 时，y=1，当x=2 时，y=1，求y关于x的函数关系式。

高等难度：

（1）求k的值。

（2）求点P到原点的距离。

这一方法能够将学生的注意力集中到某一专题或板块的训练中，从而了解到特定专题中容易出现的问题以及相关问题的解决方法，这对于提高学生的解题能力和复习效果都将产生积极的影响。

综上所述，初三阶段的复习教学对于学生的中考成绩有着极大的影响，所以教师应从多个方面出发，引领学生在掌握基础知识的同时,能够根据自身需求进行针对性复习，从而有效提高复习效率。