高中数学平面向量解题中的消元思想
2021-07-03四川省双流中学
四川省双流中学 覃 朗
高中阶段,数学是重要学科,在数学教学内容中,平面向量是重点之一。平面向量数学知识有机融合了代数知识与平面几何知识,具备较强的逻辑性和概念性,学生在实际学习中会面对各种困难,所以在解平面向量习题时,教师需引导学生掌握并灵活运用消元思想,打破思维定式的束缚,强化学生分析问题和解决问题的能力。另外,掌握消元思想解决数学问题也是高中学生必须掌握的一项技能,是学生学习和解决平面向量问题的主要思想方法。
一、消元思想在解决平面向量习题中的作用
针对平面向量题型,想要有效、快速地找到解题方法,并简化解题思路和步骤,有效拓展学生的思维,让学生确立正确的解题意识,就需要学生具备删繁就简的能力,并对于题中已知条件与设问求解之间的内在联系有正确的认知,这就离不开消元思想的应用。通过消元思想的应用,能够促使学生更好地理解与记忆相关教学知识,在很大程度上提升了学生的解题能力,提高了学生的解题效率。通过消元思想的应用,还能够有效激发学生学习平面向量知识的兴趣,促使学生主动学习相关知识,帮助学生树立学习信心。在消元思想的影响之下,学生学习平面向量相关知识,探寻有效的解决问题的方法,这是学生数学问题意识和学科素养形成的关键,有助于教学目标的实现。
二、运用消元思想解答平面向量问题的过程与步骤
平面向量数学问题大多涉及一些抽象和复杂的变量。在实际解题的过程中,每一个变量或是转化关系都需要等效代换或者进行化简操作,利用复杂的变量关系求解出某一个变量的值,这种思想与方法就是消元。在高中数学问题的解答中,消元思想既是教学重点,需要学生消化吸收,也是教学难点,非常考验教师的授课能力,合理应用消元思想,才有助于学生顺利解题。应用消元思想解答平面向量习题,主要可以分为四个步骤:
其一,审查题干。仔细审读题干,将题目中包含的数量关系、隐含条件等筛选出来,这是审读题干的第一步。同时,审读题干也是学生了解和理清题目信息的基础。只有认真审题,才能够建立正确的解题思路,对后续的解题有重要作用。
其二,依据题意,将题干条件转化成数量关系式,然后对关系式进行比较,对具备相同数值的量进行消去处理。
其三,对于题干的审查过程,如果没有找到具备相同数值的量,可以用特殊的数或者关系式分别乘两边,通过一定的变换,可以导出相应的量,从而实现变量消除,然后再应用消元思想。
其四,在应用消元思想解答高中数学中的平面向量习题后,教师还要引导学生将结果代入算式和关系式,在检查的过程验证消元思想。这样既可以帮助学生更好地理解和应用消元思想,又可以帮助学生形成谨慎的解题习惯,促使学生在消元思想的应用中能够更加灵活,实现融会贯通。
三、消元思想在平面向量中的运用
作为高中数学教学内容中的重点,数学思想与方法能够有效帮助学生理解与解答相应的习题,也是学生灵活运用所学知识解决问题的基础条件。在实际的高中数学教学中,教师要合理渗透数学思想与方法,依据具体的题目为学生分析具体的数学思想运用方法和运用技巧,还可以依据自己的经验进行总结,让学生在运用数学思想思考和解题的过程中不断提升知识运用能力和解题能力。另外,消元思想作为高中数学几何部分知识解题的重要桥梁,有机联系了代数知识与几何知识,通过相关知识的学习,能够促使学生深入了解代数与几何之间的内在联系。
1.基本定理实现消元
无论是解题教学,还是面对平面向量消元问题时,都可以运用平面向量基本定理解决实际问题。需要注意的是,这个过程不能太过于死板,因为不同题目涉及的向量也存在一定的差异,在实际解答问题时,要依据具体的题目进行基本向量的选择,然后通过实际问题的分析,有选择性地利用线性组合来表示未知向量或是其他向量,类似这样的解题方法和思想也属于消元方法的一种,体现出了转化思想。
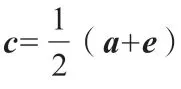
2.图像性质实现消元
消元思想不固定、不唯一,应用方法和途径较为广泛。用其解题的过程中,主要是向量的表示和相互的等效转化或是代替,然后再结合实际情况进行运算实现消元。但对于一些题目,由于涉及图形,无法应用运算法有效消元,这时就需要利用图像的性质进行消元。对于图像性质的应用,首先是图形的构建,充分利用线段中点的性质,然后再利用向量运算实现消元。另外,一些题目还需要利用一些几何知识,借助几何概念、特征和定理等才能顺利解题。此时,需要教师明确习题的分类,有效引导学生从数形结合思想与方法入手,融合与转化图形性质。对于图像性质的运用,不但可以进行消元解题,还可以借助直观真实的图像,帮助学生理解和找出不同向量间的关系,从而为消元思想解题提供可能和支持,这种综合数学思想的合理融合与应用,可以有效培养高中学生的解题能力。
例如:ABCD为任意凸四边形,A1、C1分别为AB与CD的中点,B1、B2与D1、D2分别为BC与DA的三等分点,EF为A1C1与B1D2及A1C1与B2D1的交点,求证:A1E=EF=FC1。对于这道习题的解答,需要借助平面几何的相关知识,可以在平面上任取一点O,通过点O构建各个向量,通过各条线段之间的关系,可以轻松构建向量关系,实现问题的解答。
总而言之,消元思想对于解答平面向量问题有重要作用。在实际教学中,教师要在传授平面向量知识的同时,教授学生相应的消元思想与方法,通过消元思想在平面向量不同题型中的应用,促使学生进行深度思考和学习,理清其中的向量关系,从而灵活运用消元思想与方法实现正确解题,提升学生的解题效率。
