基于高中数学核心素养理念的启思作业设计研究

河北省邯郸市第二中学 刘艳霞

核心素养是时下的流行词，高中数学核心素养包括数学抽象、直观想象、数学建模、逻辑推理、数学运算和数据分析。在数学教学活动中，作业的合理布置和交流反馈无疑是影响教学效果的重要因素，启思作业应运而生。启思作业的内容设置应针对所学基础知识、基本技能和基本方法展开，充分考量学生的知识结构和学情特点，着眼学生的未来发展和需求，培养学生的思维能力与方法、思维的层次性与逻辑性、思维的严谨性和清晰脉络，从而形成思维集成块。本质特征就是引领学生思维的形成和延伸，启发学生思维的兴趣和燃点，导引学生去探究、去尝试、去合作、去反思，使教学和学习在深层次发生，思考与探究相融而趣，以达启发思考、延伸思维、启迪智慧之目的。

一、题组策略

题组通常指一类问题的不同呈现形式，一般是在意义上、形式上、解题路径上做一些调整。目的是通过练习实现深度理解、灵活运用的效果。如三角函数求值问题题组训练。

训练一：齐次求值问题。

题组训练引导学生仔细体会“型”与“法”的内在关联，“型”对思维的启发，“法”对思维的拓延，从思维发展的角度厘清思维形成与发展的脉络，从本质上实现思维的进阶。题组训练对知识的呈现为链状结构，便于知识的深层拓展，能够挖掘出隐藏于知识背后的思想方法，从而加固加深知识的理解和迁移能力，发展学生的核心素养。

二、变式策略

启思作业的变式训练是对第一个问题的诱变，可以是同向重复变式训练，可以是异向发散思维训练。通过变式训练引导学生对问题和方法进行探究，从而及时进行归纳和反思；或者通过不同方向的散射，实现对基础知识、基本技能和基本方法的灵活理解和迁移应用，即对思维的拓延。

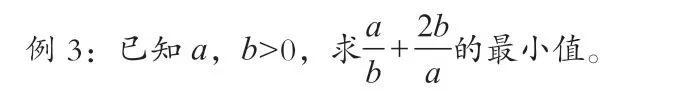
思考：根据上述问题，你能延拓出其他问题吗？针对这些问题，你能用不少于两种方法求解吗？应用基本不等式求函数最值的问题，你有哪些想法？

三、梯级策略

通常是指问题设计的梯度和层次的变化，是对问题的发散和深层次探究。目的是探究思维脉络、拓展思维向度和深刻性，从而实现深度学习的重要手段。

例4：（1）若定义在区间[a，a+2]上的奇函数f（x）满足（x1-x2）（f（x1）-f（x2））＜0，若f（1）=-2，则函数f（x）的值域为_。

（2）对于定义域为D的函数f（x），若存在区间同时满足下列条件：①f（x）在[m，n]上是单调的；②当定义域是[m，n]时，f（x）的值域也是[m，n]，则称[m，n]为该函数的“和谐区间”。下列函数存在“和谐区间”的有（ ）。

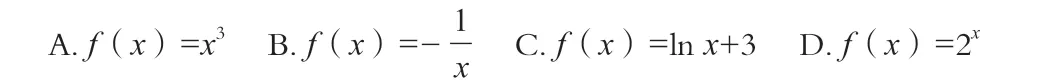
点拨：两个问题两个层面，一个侧重知识的宽度，一个展现思维的厚度和深度，是训练思维、拓展思维、实现进阶的有效题型。

梯级训练重在强调思维的内化、深化，重在联系联想。从一个小的问题出发，逐步丰满其体量，丰富其内涵，建立广泛的联系和联想，实现对问题的深化理解，逐步实现深度学习、深度思维。

启思作业的开发和设置就是要在启思上做文章，通过不同的作业模式，满足不同学生的发展需要，激发每个学生数学学习的兴趣，将自主学习与合作探究深度融合，真正做到优等生吃得饱、中等生吃得好、学困生吃得消，从而使不同的学生在数学学习上得到不同的发展，真正落实核心素养，提升学生的数学应用和创新意识，发展学生的关键能力和必备品格，培养德智体美劳全面发展的社会主义建设者和接班人。