培养自主学习能力，提升初中学生数学学科素养

江苏省启东市继述中学 施婧婧

当前，初中学生最缺的就是自主学习能力，他们不会主动提问，不会主动拓展，不会主动将认知转化为能力，一言以蔽之，他们的学习以被动为主，以教师布置任务为主。要改变学生被动学习的现状，教师就要改变教学方式，培养学生自主学习的意识，进而让自主成为习惯，让学习成为自然。

一、培养学生自主发现问题的习惯

培养学生自主学习的能力首先要培养学生自主发现问题的能力。学生习惯了只完成教师布置的作业，不愿意多思考，其实只有养成自主找寻问题的习惯，进而去解决问题，才能提升能力。自主发现问题能让学生发现认知的本质，能发现自己思维的特点。以人教版初三数学下册“锐角三角函数”为例，教师设置这样的题目：如图1 所示，在Rt △ABC中，∠C=90°，AC= ，BC= ，解这个直角三角形。

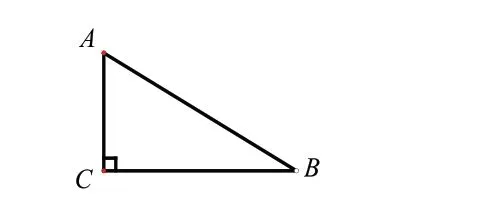
图1

学生几乎没怎么动脑筋就解答出这道题，即A=30°，B=60°，AB=2 。在学生做完之后，教师提问：大家能不能从这道题中发现一些问题呢？学生就开始思考这道题还传达了哪些信息，通过解答这道题有哪些收获。学生对照着原题，想想条件与结论，进而发现了这样的问题：要确定一个直角三角形的形状和大小，至少需要知道哪些元素呢？由此延伸出另外一个问题：直角三角形中到底有几个元素？在这些元素中，除直角外，如果再知道两个元素，这个三角形是不是就可以确定了？一个看似简单的问题，如果让学生带着一双发现的眼睛来分析，他们会发现更多奥秘。让学生主动发现问题，能将他们从题海中解放出来，能给他们更多思考的时间。

二、培养学生主动进行小组合作的习惯

培养学生自主学习的习惯就是要提升他们解决问题的能力，就是要让他们成为学习的主人。学生在学习数学的过程中经常会遇到一些难题，要解决这些问题，靠自己的力量可能不够，这时候就可以借助小组的力量，自主去找寻解决问题的突破口。遇到难题的时候，大多数学生想到的可能是老师会讲，等明天再说。其实采取合作的方式往往能让学生有更多机会主动学习，能使学习成为自己的事，别人只要稍微点拨，问题也许就会迎刃而解。

以人教版初三数学上册“实际问题与二次函数”为例：已知某商品的进价为每件40 元，现在的售价是每件60 元，每星期可卖出300件。市场调查反映：如调整价格，每涨价1 元，每星期要少卖出10件；每降价1 元，每星期可多卖出20 件。如何定价才能使利润最大？学生遇到这样的题目可能毫无头绪，不知道题目讲述的重点是什么，要从题目中找出怎样的等量关系。这时候，小组长会提醒学生：如果设该商品定价为x元，利润为y元，是不是就可以列出一个关系式？这样的提醒能让学生将繁杂的题目转化为定价与利润之间的关系描述。当学生还是一脸茫然时，小组长又提醒他们分组讨论。自然地，学生就将x、y分成不同的情况来讨论：当x＞60 时，y=（x-40）×[300-10（x-60）]=-10x2+1300x-36000， 当x=65 时，ymax=6250。有学生以为讨论可以结束了，小组长说：既然有x＞60 的情况，那么x＜60 会是怎样？于是学生发现当x＜60 时，y=（x-40）×[300+20（60-x）]=-20x2+2300x-60000，当x=57.5 时，ymax=6125。由此推断当x=65 时，ymax=6250，即定价为65 元时，利润最大。明显地，是小组合作学习推动了自主学习的深入。

三、培养学生主动拓展能力的习惯

学生在学习数学的过程中经常会出现浅尝辄止的现象，这说明学生没有长久地坚持自主学习，也说明他们自主学习的深度不够。其实对学生来说，自主学习还意味着要不断拓展学习的深度，要让自主成为推动学生多元能力生成的动力。

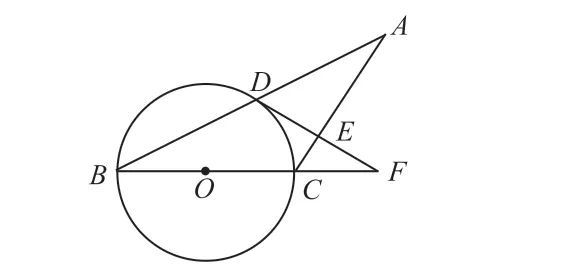
图2

以人教版初三数学上册“直线和圆的位置关系”为例：如图2 所示，△ABC中，AC=BC，以BC为直径的⊙O交AB于D，过点D作DE⊥AC于点E，交BC的延长线于点F。求证：AD=BD。当学生连接CD后，发现BC是直径，就能推断出CD⊥AB，再从BC=AC中推断出BD=AD。有了这样的结论之后，学生就开始进一步思考：能不能从这道题目中发现更多规律？因为这一课学的是直线与圆的关系，于是他们想到DF是不是⊙O的切线？在自主学习的理念背景下，教师要进一步拓展学生这方面的能力。学生从OB=OD能推断出∠B=∠BDO，再从BC=AC中推断出∠B=∠A，∠A=∠BDO，所以OD//AC，而DE⊥AC，自然就推断出OD⊥DF，进而就有了DF是⊙O的切线。

可见，学生学习数学的过程就是提升数学素养的过程，要提升学生的数学素养，最重要的就是提升他们自主学习的能力。