多措并举，深度复习

江苏省扬州市汤汪中学 孙东明

初中复习阶段时间紧、任务重，为了提高复习的质量和效益，教师需要选择多种举措落实深度复习，促使学生逐步掌握初中阶段的复习重点，提高备考效率。

一、夯实基础，构建知识网络

夯实基础要求学生把握基础知识与基本技能，也就是通过复习各单元知识结构，构建知识网络，从而了解到知识点之间的联系。

在二次函数的复习中，可以引导学生总结函数的解析式，即：

一般式：y=ax2+bx+c（a≠0）。

顶点式：y=a（x-h）2+k（a≠0），顶点的坐标为（h，k）。

两根式：y=a（x-x1）（x-x2）（a≠0），与x轴的交点为（x1，0），（x2，0）。

除了解析式外，基础知识还包括二次函数的性质、二次函数的图像与a、b、c的关系、二次函数与一元二次方程的关系。

二次函数的图像与a、b、c的关系：a决定抛物线的开口方向；a、b决定对称轴的位置；c决定抛物线与y轴交点的位置。

二次函数与一元二次方程的关系：二次函数图像与x轴的两个交点的横坐标x1，x2，是对应一元二次方程的两个实数根。

通过这一基础夯实过程，学生能够对二次函数知识有更为全面的把握，同时能够从已构建的知识中进行迁移和拓展，从而提高复习效果。

二、整体规划，细化复习方案

为了贯彻课标内涵，做到深度复习，教师应重视对复习方案的细化，要让学生了解到如何展开有效复习，如何稳扎稳打地提高复习效果。在一元二次方程的复习中，教师可以按照“基础知识—模拟训练—巩固提升”三个步骤进行复习。

1.基础知识盘点

总结一元二次方程的概念：

（1）只含有一个未知数，未知数的最高次数是2，且系数不为0，是整式方程。一般形式为ax2+bx+c=0（a≠0）。

（2）总结一元二次方程的解法：

①直接开平方法：形如（x+a）2=b（b≥0）的方程，x+a=± ，所以，x1=-a+ ，x2=-a- 。

②配方法：形如ax2+bx+c=0（a≠0）的方程，可通过化形、移项、化系数为1、配方这一过程完成。

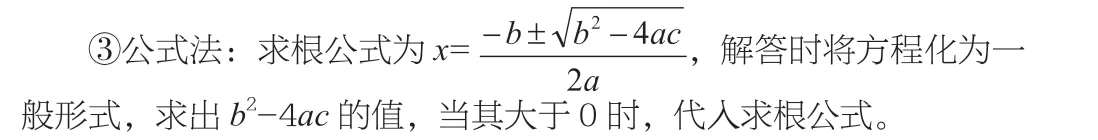
④因式分解法：提公因式法、公式法、十字相乘法。

2.模拟训练

教师可以为学生提供与一元二次方程相关的训练题，如：

（1）解方程：（2x+3）2=4（2x+3）；9x2+6x+1=0。

（2）有一面积为150 m2的长方形鸡场，鸡场的一边靠墙，墙长18 m，另三边用竹篱笆围成，竹篱笆长为35 m，求鸡场的长和宽各为多少？

在选择或设计模拟训练题的过程中，教师要充分考虑问题的内容、难度，使其能够满足不同层次学生的需求。

3.巩固提升

教师可以在巩固提升阶段借助试卷考试，引导学生进行错题分析，使下一步的复习更具针对性。

三、专题训练，提高综合能力

专题训练能够以专题的形式帮助学生一步步掌握复习的重点知识，提高综合能力。为了发挥出专题训练的最大效果，专题的选择要准、划分要合理，如此才能使学生在专题训练中强化复习效果。

针对方程型的专题训练，要引导学生按照顺序训练，即：找出题中的等量关系、设未知数、列方程、解方程、检验方程。

如：某电脑公司受经济危机影响，今年三月份甲种型号电脑每台售价比去年同期降价1000 元，如果卖出相同数量的电脑，去年销售额为10 万年，今年只有8 万元。

（1）今年三月份电脑每台售价多少元？

（2）为增加收入，公司决定销售乙种型号电脑，乙种型号电脑每台进价3000 元，甲种型号电脑每台进价3500 元，公司预计用不多于5 万元、不少于4.8 万元的资金购进两种电脑共15 台，有几种方案？

对该问题的解决主要训练了学生对函数方程的应用能力，对于学生建立两个变量之间的等量关系具有重要作用。

总之，为了提高学生的复习质量，教师绝对不能忽视对多种举措的应用，反而应该结合复习大纲和学情有效落实对学生的深度复习引导工作，进而提高学生的整体复习效果。