电动汽车悬架结构设计和动静态特性分析与优化
2021-07-03尹垂鹏钟海龙黄彦青雷铭民汪毓鑫
尹垂鹏,钟海龙,黄彦青,雷铭民,汪毓鑫
(华南理工大学广州学院,广东 广州 510000)
引言
汽车的基本的动力性要求已无法满足时代的要求,因此,对汽车的稳定性、操纵性和安全性的要求变得日益严格,而悬架在此方面充当着不可或缺的角色。
麦弗逊作为悬架中的经典代表,虽然存在着不足,但其简洁的结构与制造成本低等优点也为其在悬架市场中占有一份不小的地位。而对麦弗逊前悬架进行虚拟样机实验能够达到真实悬架的实验效果,且相较于传统的实车实验,虚拟样机实验设计周期短,工作效率高等优点也为悬架的优化设计带来了便捷。
Adams软件在机械系统的动力学以及力学分析中有着较为突出的作用,通过Adams对悬架进行仿真分析并将悬架的参数进行优化处理,得出较为理想的参数,并将仿真实验结果与实车相结合,经过不断尝试与分析将麦弗逊悬架进行优化从而提高整车的基础性能。
1 麦弗逊悬架建模分析
1.1 麦弗逊悬架结构分析
本文所建立的悬架模型为麦弗逊式,主要组成包括转向节、减震器、螺旋弹簧、转向器、车架、转向横拉杆以及三角臂。悬架之间通过各运动副以及铰链连接构成麦弗逊悬架模型。
1.2 仿真条件的假设
(1)车辆相对于地面静止。
(2)所有的零部件均为刚体,不会因为轮跳的影响而变形。
(3)忽略摩擦力以及各零件之间的间隙。
1.3 麦弗逊悬架的建立
1.3.1 建立悬架所需参数
对于悬架模型的建立,悬架所需的各项硬点坐标如表1所示,决定着悬架各部分的空间位置分布情况,如果硬点坐标设计得不合理,将会直接影响整车的性能。整车相关参数如表2所示。本次研究将从厂家所获得到的悬架各硬点参数以及整车的相关性能参数代入悬架子系统中以便接下来的仿真优化分析。
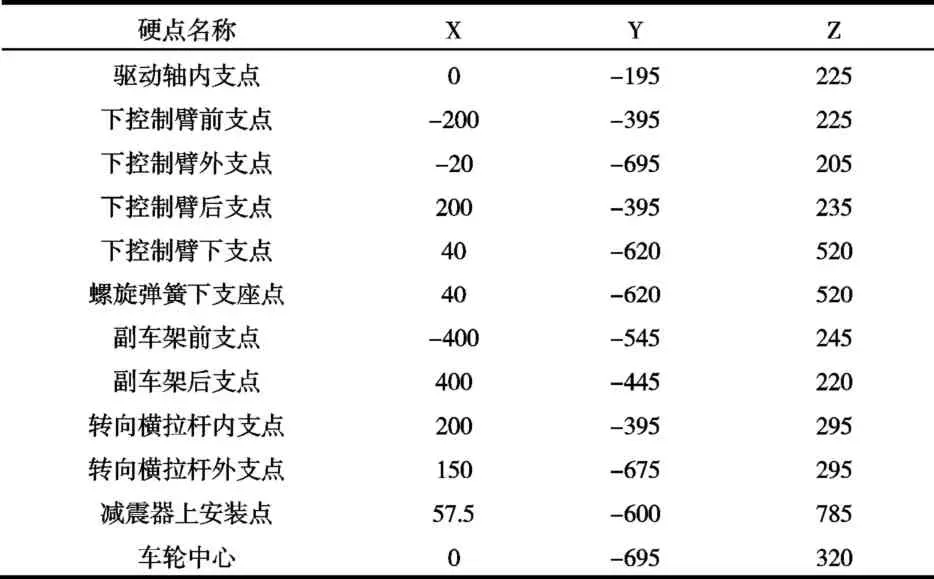
表1 建模所需的硬点参数
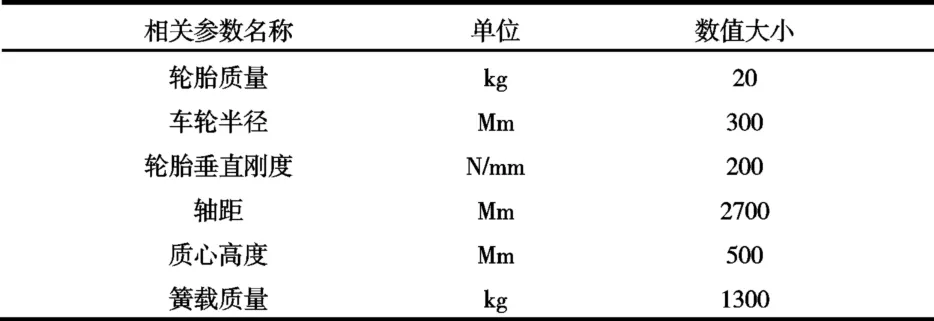
表2 整车相关参数
1.3.2 螺旋弹簧以及减震器的相关参数
在图1中,上部分表示螺旋弹簧的刚度变化曲线,下部分为减震器的阻尼变化曲线,从图中可以看到其变化情况都处于非线性状态,充分说明了螺旋弹簧与减震器共同起到缓冲减震的作用。

图1 螺旋弹簧刚度及减震器阻尼变化曲线
1.3.3 悬架模型的建立
结合上述所得到的各硬点坐标以及弹簧与减震器的变化曲线,可在三维软件中建立如图2所示的悬架模型。

图2 麦弗逊悬架模型
1.3.4 悬架运动学分析
此独立悬架所对应的各约束副的种类及数目如下表3所示。

表3 约束副的种类及数目
麦弗逊前悬架的约束度:F=13x6-4x4-4x2-3x4-5x4-6x3=4。
由上图计算所得,悬架有4个自由度,其中2个为车轮的跳动,2个为前轮绕主销轴线的转动。
2 麦弗逊前悬架的运动学仿真过程
本次实验利用Adams/car进行仿真,在对麦弗逊悬架进行仿真过程中,在软件中导出悬架子系统模型,再将已获得的数据代入构建出悬架模型,设置如图3所示的悬架构建所需的基本参数,在仿真过程中对汽车在±50mm的道路上观察汽车双轮同向及异向跳动的仿真情况,找出悬架各定位参数的变化范围并对其展开分析,针对上一步中发现的问题,找出不符合理想范围的定位参数,将其定位目标函数,用以下一步优化分析[1]。
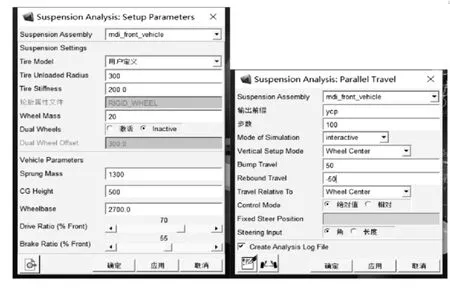
图3 构建悬架所需参数
3 双轮同向跳动仿真分析图
3.1 前轮前束角分析与仿真
3.1.1 前轮前束角定义
前轮前束角是指汽车车轮中心与纵向中心平面所成的角度。两车轮内八排列为正的前束角,反之则为负值,左右车轮的前束角之和为总前束角。
3.1.2 前束角的影响
前束角的存在能够在一定程度上弥补外倾角所带来的影响,在车轮的设计中前束角能够抵挡外倾角所带来的偏转,并且保持车辆在平直道路上的直线行驶的稳定性,不良的前束角可能会导致车胎过度磨损以及破坏行驶平稳性。
3.1.3 前束角变化曲线图
图4为前束角的变化曲线图,横坐标为轮跳行程,纵坐标为前束角度,车辆进行±50mm的跳动仿真实验,前束角变化标准范围在±0.5之间。
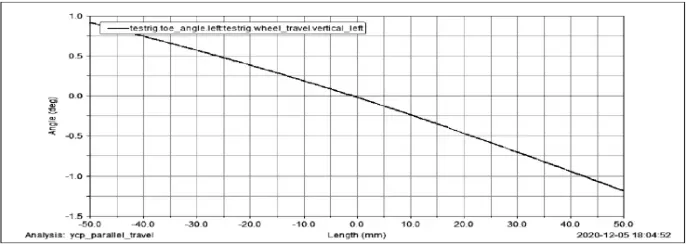
图4 前轮前束随轮跳行程的变化曲线
图4所示的前束角变化范围为-1.194~0.881,变化幅度为2.075,相对于理想的变化范围±0.5来说较为不合理,因此将其作为下一步的优化对象进行优化。
3.2 前轮外倾角分析与仿真
3.2.1 前轮外倾角定义
车轮中心的汽车横向平面与车轮平面的交线和地面垂线之间的夹角称为前轮外倾角。
3.2.2 前轮外倾角的影响
安装车轮时应使车轮具有一定的外倾角,可以使轮胎均匀磨损并减轻轮毂外轴承的负荷,以防止车轮内倾,同时,外倾角也可以与拱形路面相适应。但外倾角不宜过大,否则会使轮胎产生偏磨损[2]。
3.2.3 前轮外倾角的变化曲线图
图5为前轮外倾随车轮上下跳动的变化曲线。一般要求前轮外倾角在-1°到2°之间变化,从图中看出,前轮外倾角的变化范围为-0.335°~0.961°,变化量为1.297,在理想范围之内,在后期的优化过程中,不需要把它作为一个目标函数,但也应将其导入变化参数,使其处于理想范围之中。

图5 前轮外倾随轮跳行程的变化曲线
3.3 主销后倾角分析与仿真
3.3.1 主销后倾角定义
在汽车的纵向平面内,汽车的主销向后倾斜,主销轴线和地面垂直线的夹角叫主销后倾角。
3.3.2 主销后倾角的影响
合理的主销后倾角对汽车在行驶过程中的稳定性起着关键作用,且有使方向盘自动回正的作用,车轮在自动回正时,往往有着一个稳定力矩,调整主销后倾角能够调整稳定力矩的大小。
3.3.3 主销后倾角的变化曲线图
图6为主销后倾角随车轮行程的变化曲线图,主销后倾角取值的理想范围为3°~10°,从图6中可以看出,主销后倾角的变化区间在7.0°~9.363,其值符合理想的变化区间。
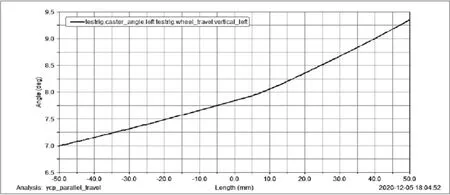
图6 销后倾随轮跳行程的变化曲线
3.4 主销内倾角分析与仿真
3.4.1 主销内倾角定义
从上往下看汽车,主销顶端向内倾斜的特性叫主销内倾。主销轴线与地面垂直线在汽车水平面上的角度称为主销内倾角。
3.4.2 主销内倾角的影响
主销内倾角在汽车自动回正功能中起主导地位,且还可使汽车在转向时加在转向盘上的力减小。
3.4.3 主销内倾角的变化曲线图
图7为主销后倾角随轮跳行程的变化曲线图,主销内倾角的取值范围为5°~15°,从图7可以看出,主销内倾角在理想的范围之内,若主销内倾角过大,则会在车轮绕主销偏转的转向过程中,轮胎与路面间将产生较大的滑动,摩擦力增大,造成转向沉重,轮胎磨损加剧。

图7 主销内倾随轮跳行程的变化曲线
3.5 主销偏移距分析与仿真
3.5.1 主销偏移距的定义
主销偏移距是指地平线与主销轴线的交点至车轮中心平面与地面的交线在汽车行驶平面的投影距离,主销偏移距存在着正负,偏移距在车轮中心线与地面交点的里面为正,反之为负。
3.5.2 主销偏移距的影响
主销偏移距主要目的是减小停车转向力,如果停车转向,则车轮将绕c点边滚边滑,可在某种程度上减小转向阻力。当偏移距为负,在左右车轮制动力不相等时可抵抗汽车改变行驶方向,但偏移距为正时,则无此效果。
3.5.3 主销偏移距的变化曲线图
图8为主销偏移距随轮跳行程的变化曲线图,从图中可以看出其在理想范围内。
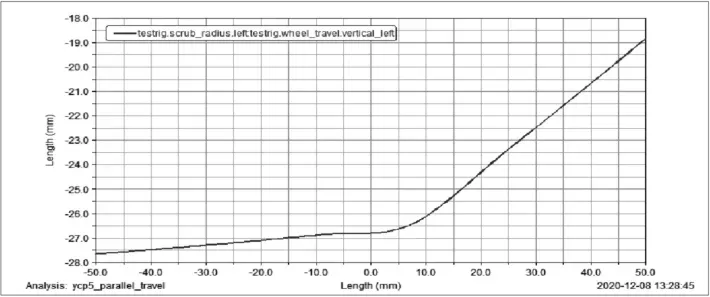
图8 主销偏移距随轮跳行程的变化曲线
3.6 车轮轮距分析与仿真
3.6.1 车轮轮距的定义
车轮轮距是指车轮在同一水平面上两点之间的距离。
3.6.2 车轮轮距的影响
一般来说,车轮轮距越宽,驾驶的舒适性就越高,更宽的轮距能提供更好的稳定性,车辆横向倾斜行驶时,外侧的车轮能提供更好的支撑,但轮距过于宽大也会影响汽车的安全性,因此,轮距应与车身高度相适应[3]。
3.6.3 车轮轮距的变化曲线图
图9为车轮轮距随轮跳行程的变化曲线图,一般要求车轮轮距在±5mm之内,从图中可以看出,车轮轮距的变化范围为-0.39~6.02,相较于理想范围有较大的变动,不符合理想范围,所以需要对此参数进行优化。
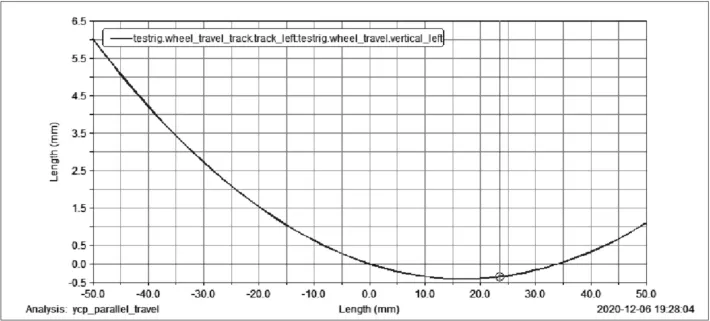
图9 车轮轮距随轮跳行程的变化曲线图
4 双轮异向跳动的仿真分析
对于双轮异向跳动分析,在实际生活中模拟的是车身侧倾所引起的悬架变化,在Adams软件中,对其施加一对大小相等、方向相反的力,使其运动,进而得出各定位参数与轮跳行程的变化规律[4]。
图10为双轮异向跳动与同向跳动两种情况下各定位参数的变化曲线图,其中图(a)为前轮前束,图(b)为前轮外倾,图(c)为主销后倾,图(d)为主销内倾,图(e)为主销偏移距,图(f)为车轮轮距。 从图中可以看出,当车轮同向与异向跳动时,其随轮跳行程的变化规律几乎保持一致。根据车轮同向与异向跳动的仿真结果分析可得,车轮定位参数中,前轮前束角与车轮轮距需要优化设计。
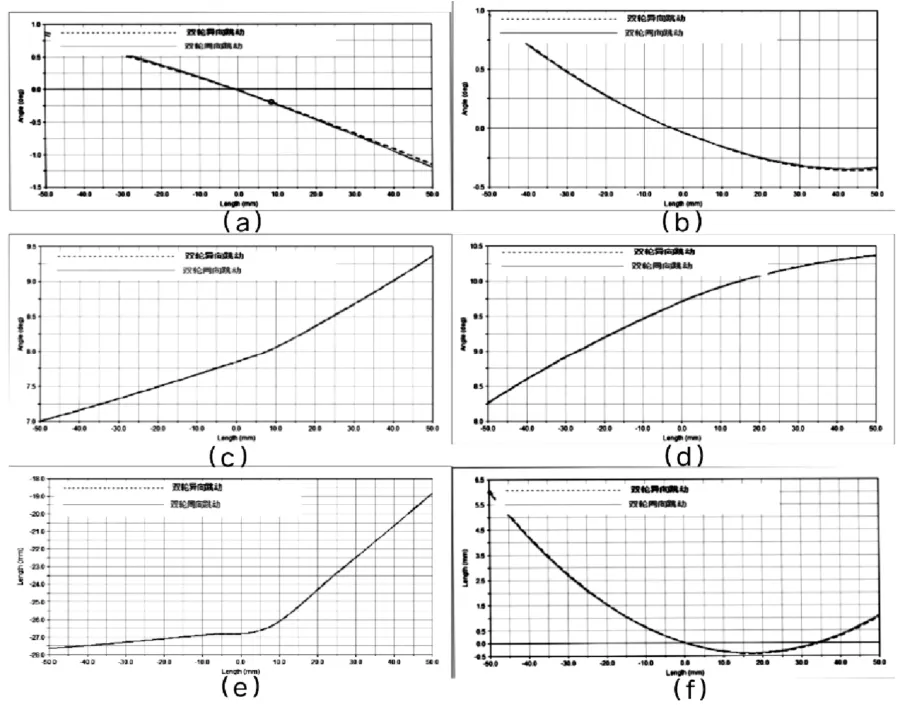
图10 各定位参数随轮跳行程的变化曲线图
5 悬架的优化设计
在上文针对麦弗逊悬架进行了一系列的研究,通过对比车轮同向跳动与异向跳动随轮跳行程的变化,分析得出了悬架存在以下的问题:车轮的前轮前束角与车轮轮距不满足理想范围。因此在接下来的优化设计中,需用到Adams/insight对其进行优化设计,保证汽车具有良好的行驶性。
5.1 Adams/insight简单介绍及分析
Adams/insight提供了对实验结果进行各种专业化统计分析的工具。可规划和完成一系列仿真实验,作为选装模块,既可以与其他软件模块共同工作,也可以脱离Adams环境单独运行。若实验因素较多,导致模拟实验的次数增加,就可利用Adams/insight中的DOE Screening(2Level)对多个需要设计变量进行优化。
5.2 悬架优化实验分析
在悬架系统中,硬点参数的改变会导致悬架的性能不断发生变化,为了能够获得目标函数的最优解,必须对各设计变量设定一定的变化范围。先通过试验设计,找出对悬架影响较大的因素,然后再将其作为设计变量,对其进行优化。
在Adams软件所建立的矩阵中,常将行表示实验运行的次数,列表示因素,在相关的调查方法中,共有Study-Peri-meter、Study-Sweep、DOE Screening(2 Level)、DOE Response Surface、Variation-Monte Carlo、Variation-Latin Hypercube等6种方法,但在本次实验中,重点是要选取对样机性能影响较大的几个设计变量,所以本次实验选取DOE Screening(2 Level)来进行实验优化。
5.3 实验优化设计
(1)在软件中导入之前设计好悬架模型,将利用Adams/insight研究如何通过调节硬点的位置,分析车轮上下跳动时其对前束的影响。
图11 Adams/insight对话框
根据上述所做的实验分析及参考各类资料文献可知,在对所建立的麦弗逊悬架保证其各参数在理想区间的情况下,对各硬点坐标改动得越少越好,因此实验选取了转向横拉杆内支点Y、Z坐标、外支点Y、Z坐标、下控制臂外支点Y、Z坐标,前支点Y、Z坐标、后支点Z坐标、减震器上安装点X、Y、Z坐标等12个设计变量。
(2)在确定所需要设计的变量后,在experiment目录下的ground中找到需要优化的12个设计变量,再将各实验变量都添加至factors内,将其作为优化设计矩阵的因素,再通过软件对所选择的因素指定所示的范围,使之构成设计空间Design Space。
图12 设计因素的属性及实验策略
试验矩阵的建立如图13所示,其中横方向代表设计因素,纵方向代表着实验所进行的次数。且-1表示该处取最小值,+1表示该处取最大值。

图13 试验矩阵
通过软件进行设计矩阵中的试验迭代后,所选取的12个设计变量则根据上述的试验设计所确定,所选取的变量对于目标函数都有着较大的影响,优化后所得到的硬点坐标与原坐标对比如表4所示。
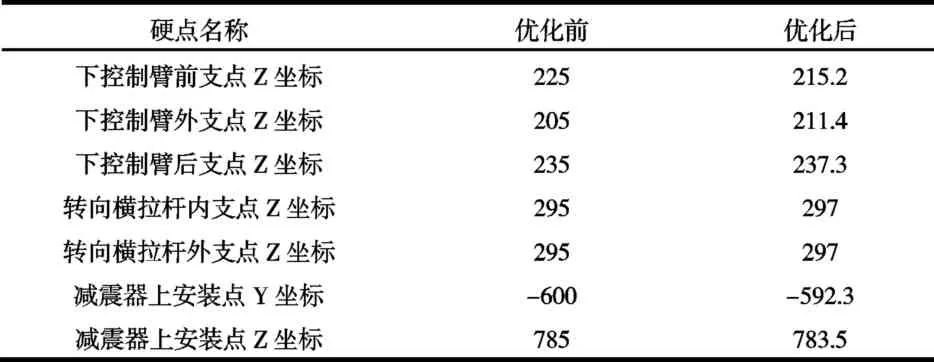
表4 优化前后的硬点坐标
6 悬架优化前后对比
根据上文优化所得到的硬点坐标,将其带入到先前所建立的麦弗逊悬架上,并再次对其进行定位参数随轮跳行程的仿真实验,得出优化前后各目标函数的变化情况如图14所示。其中图(a)为前轮前束角优化前后对比曲线图,图(b)为前轮外倾角,图(c)为主销后倾角,图(d)为主销内倾角,图(e)为主销偏移距,图(f)为车轮轮距。
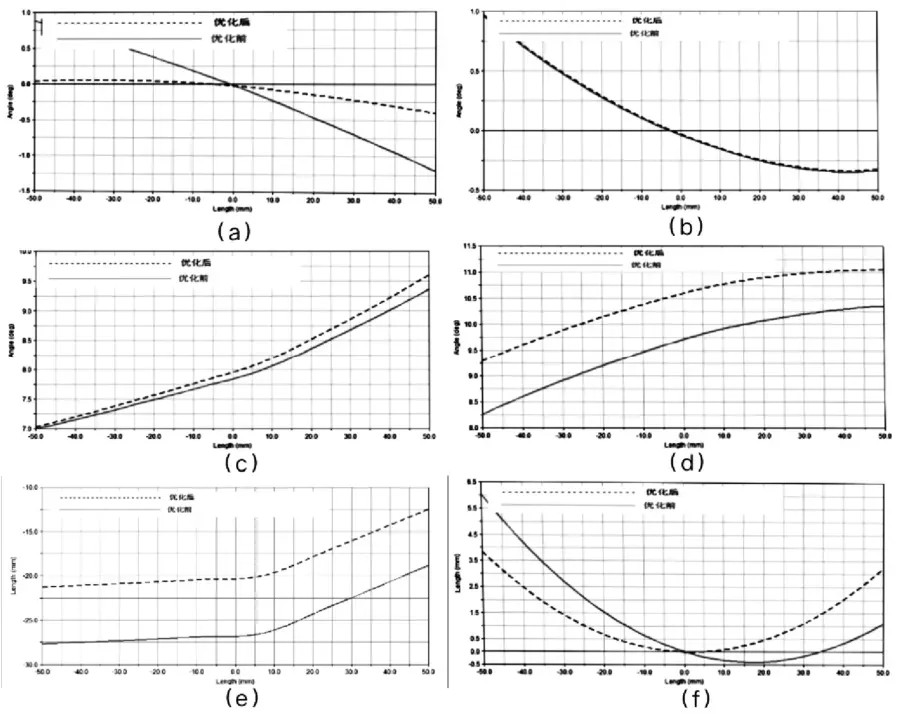
图14 各硬点坐标优化前与优化后对比图
通过优化分析结果可得知,优化过后悬架的各定位参数均在理想范围之中,前轮前速以及车轮轮距的变化量相比较优化前有着较大的改善,悬架性能有所提高,车辆的操纵稳定性以及舒适性都有一定的改善。
7 总结
本研究在麦弗逊悬架仿真优化分析中,充分利用了Adams软件的仿真建模及其对于多变量分析优化的优点,确认优化过程中的相关设计变量和目标函数,实现了对多目标函数的优化,一定程度上提高了车辆在行驶过程中的操纵稳定性以及舒适性。
