基于特定偏振态成像的水下图像去散射方法
2021-07-02褚金奎张培奇成昊远
褚金奎,张培奇,成昊远,张 然
(大连理工大学辽宁省微/纳米技术与系统重点实验室精密与特种加工教育部重点实验室,辽宁大连116024)
1 引 言
我国拥有400 多万平方公里的海洋国土,至今仍有大量的海域尚待探索开发。在资源紧张、人口膨胀的情形下,开发和保护海洋资源是一项影响深远、面向二十一世纪的战略选择[1]。这催生了水下图像恢复和增强技术的开发和研究。水下成像技术在生物探测、资源勘探和水下导航等多个领域有广泛而深入的研究和应用[2-6]。然而水体会造成光线的吸收和散射,使得水下成像效果较差。吸收作用降低光线能量,使光强呈指数衰减;散射作用则是一个复杂的过程,可分为前向散射和后向散射,其中前向散射导致成像光线偏离原来方向,降低图像分辨率,后向散射则会干扰目标光线,降低图像对比度和产生背景噪声[1]。因此,分析水下成像的散射过程,提高成像质量是一项富有挑战性的工作。
为提高水下成像的清晰度,许多研究人员致力于消除水下散射对图像的影响。如今工作主要集中于非物理模型算法和物理模型算法。非物理模型算法将传统图像处理手段应用于水下图像质量改善[7-8],虽然实现简单且计算复杂度低,但忽视了水下成像的物理模型,导致图像失真、噪声放大。基于物理模型的算法依赖对先验条件的准确估计,在不同的成像环境下,相应的先验条件将会改变,这限制了算法的普遍适应性[9-11]。
在相同辐射的情况下,不同物体的状态(如材料的理化特征、表面粗糙度、几何形状等)会产生不同的偏振状态,形成偏振光谱[12]。因此采用偏振手段可在复杂的辐射环境中,检测出目标信号[13-14]。偏振差分成像[15-16]是一种经典的水下成像方法,其通过共模抑制放大器来抑制后向散射光,放大目标信号光。但因光学偏振片机械转动,使得该方法可靠性差、耗时长,难以满足实际环境下的实时探测[17-18]。
针对上述问题,本文引入斯托克斯矢量和穆勒矩阵,通过建立水下偏振成像的物理模型分析水下散射的影响,提出了一种自适应的基于特定偏振态的水下图像去散射方法,最后利用水下实时偏振成像系统进行水下环境下的成像对比实验,验证该方法的可靠性。
2 原 理
2.1 水下成像模型
基于物理模型的方法是通过估计水下退化过程中的关键参数,获得清晰的水下目标图像。偏振相机在相机坐标系(x,y)处获得的光强图像[19-20]可表示为:
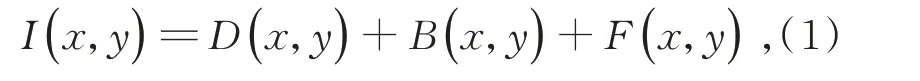
其中:D(x,y)表示传感器接收到的目标信息光。B(x,y)表示光源由水体散射到传感器的后向散射光。F(x,y)表示部分目标信息光由于水体散射产生的前向散射光,如图1 所示。
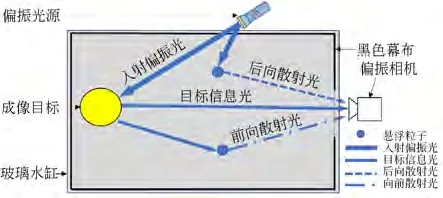
图1 实验原理及装置图Fig.1 Experimental principle and device diagram
目标信息光D(x,y)和后向散射光B(x,y)为:
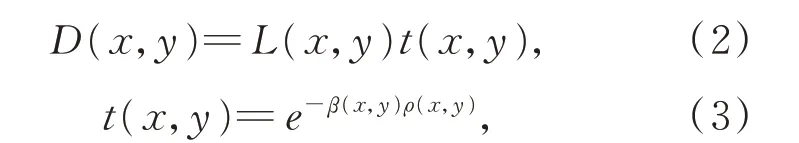
其中:L(x,y)是衰减前的目标光强,A∞对应无限远处的水下环境光光强,t(x,y)为介质透射率,可表示为:
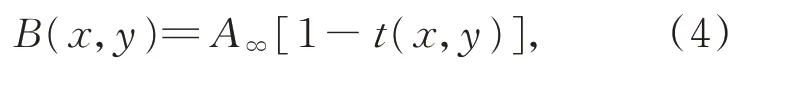
其中:β(x,y)是衰减系数。在单一均匀介质中,衰减系数β(x,y)在空间上是不变的,且β(x,y)=β0。ρ(x,y)表示传播距离,该距离是指物体与相机之间光路的水下部分。
根据以上等式,物体辐射率L(x,y)为:
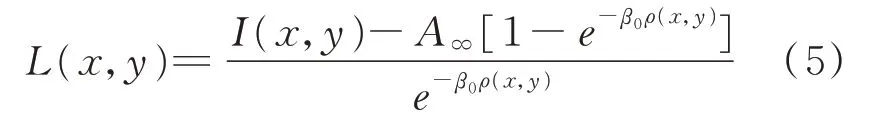
2.2 偏振成像原理
通常,斯托克斯矢量S被用来描述光的偏振态:
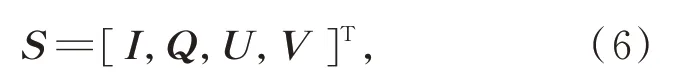
其中,I是投影在成像传感器上的光强,Q是0°和90°方向偏振分量的光强差,U是45°和135°方向偏振分量光强差,V是左旋和右旋圆偏振分量的光强差。当入射光S=[I,Q,U,V]T经过偏振片,偏振状态改变,可以使用穆勒矩阵表示:
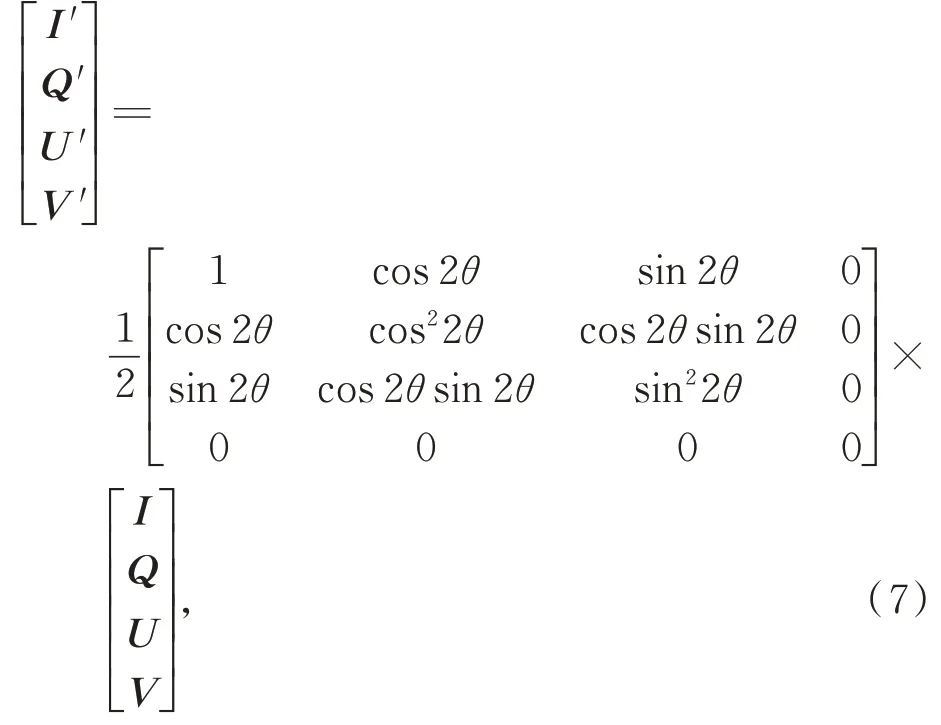
其中:θ是主光轴与参考线之间的夹角,S′=[I′,Q′,U′,V′]T表示出射光线。通过穆勒矩阵的第一行得出公式:
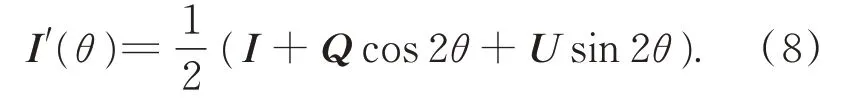
因此,通过获取三个不同的θ值的出射光光强,可计算入射光束的I,Q和U值。此处,偏振相机可获得θ为0°,45°,90°和135°的光强图,如图2 所示,可得到以下方程组:
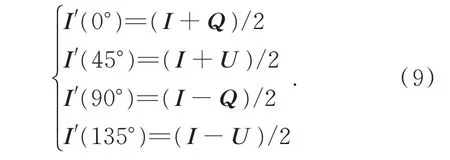
方程组可进行如下转换:
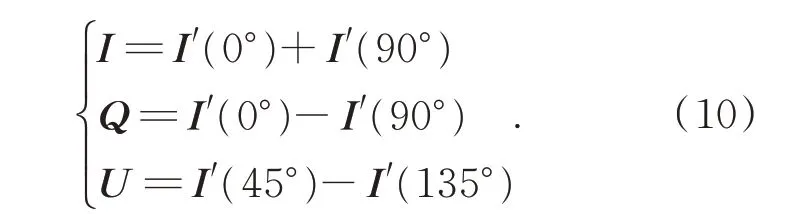
可得到入射光的线偏振度P(以下简称偏振度)及偏振角χ:
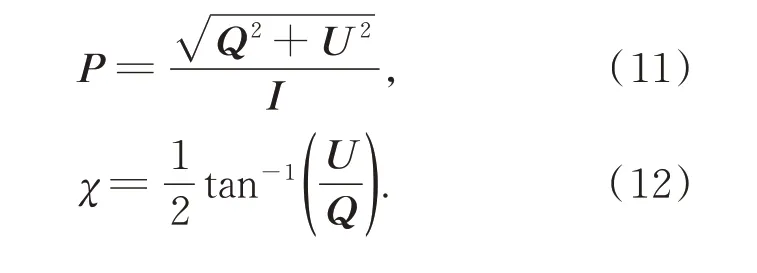
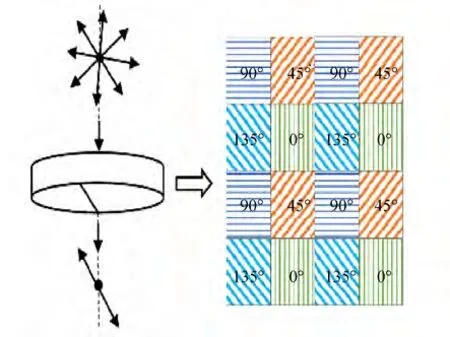
图2 偏振相机测量原理Fig.2 Measurement principle of polarization camera
2.3 特定偏振态去散射
任何一束光可用斯托克斯矢量S的形式描述:
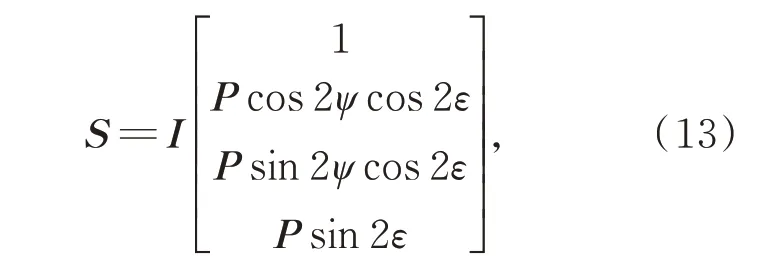
其中:I是总光强,P是偏振度,ψ是方位角,ε是椭球率。当光束是线性偏振时,可将椭圆偏振光设为0°。为简化计算,模型假定单位强度,则入射光的斯托克斯矢量形式可写为:
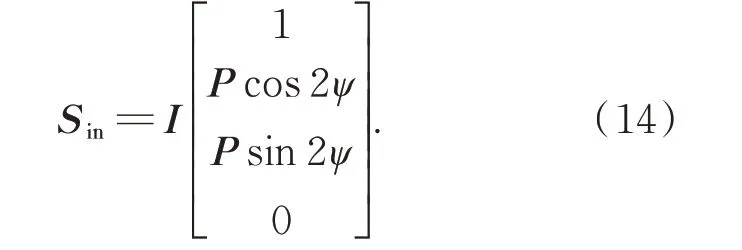
当入射偏振光穿透到水中,光束与悬浮粒子产生散射作用,入射光和经散射后的出射光的斯托克斯矢量可通过穆勒矩阵建立以下关系:
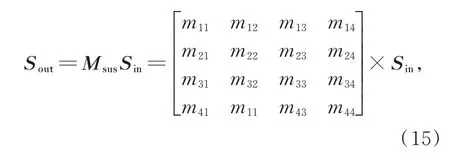
其中,穆勒矩阵Msus的元素(mij)(i,j=1,2,3,4)取决于散射粒子的复折射指数、形态、尺寸、入射电磁波波长及散射角。
同理当入射偏振光光束与成像目标发生反射,入射光和反射光的斯托克斯矢量可通过穆勒矩阵建立以下关系:
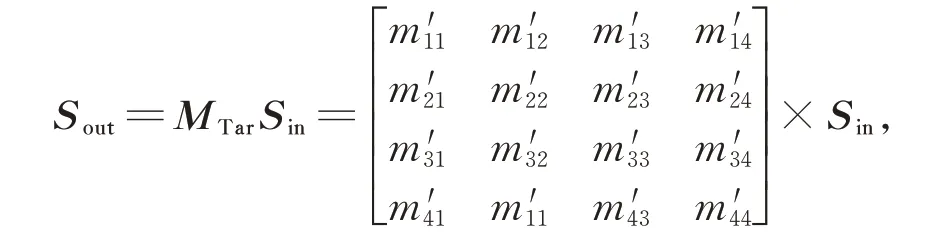
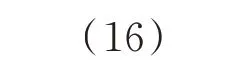
其中,实穆勒矩阵MTar的元素(m′ij)(i,j=1,2,3,4)由光线的入射角和物体本身性质(如材料的理化特征、表面粗糙度、几何形状等)决定。
因此,使用偏振光作为光源,进行浑浊水体的偏振成像,传感器接受到目标信息光的斯托克斯为:
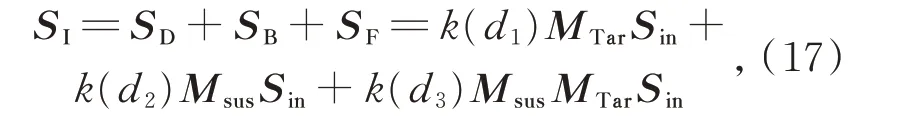
其中k(d i)表示水体吸收系数(i=1,2,3),与光束传播距离相关。
将公式(14)~公式(16)带入公式(17),则目标信息光的斯托克斯矢量为:
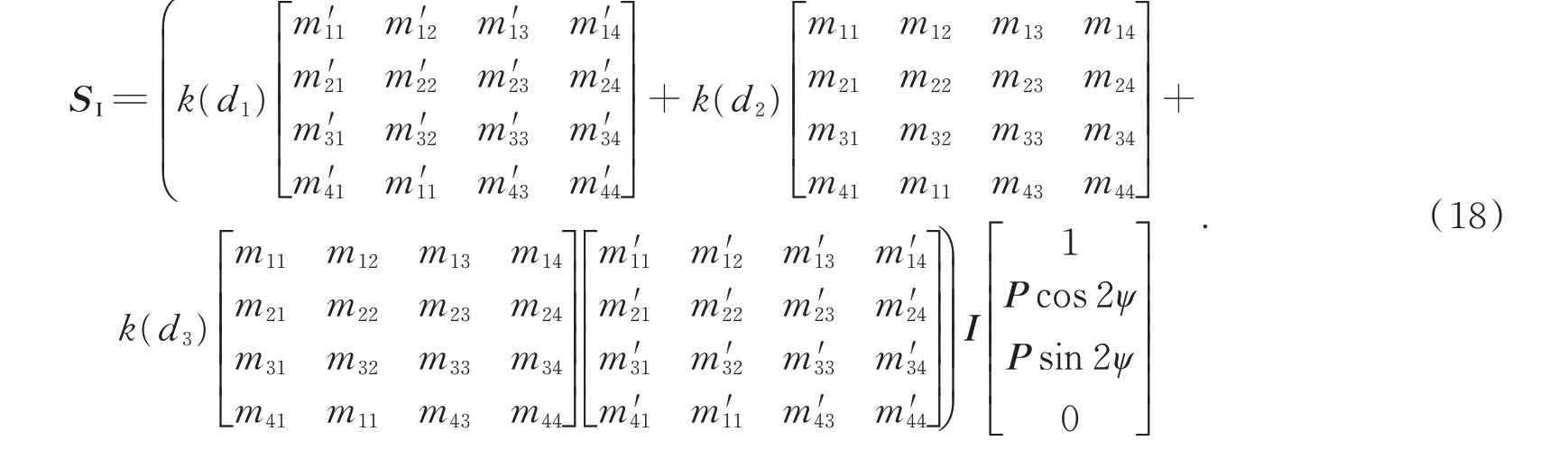
由公式(18)可知,悬浮粒子的散射将改变入射光的偏振状态,这造成传感器接收目标信息光的偏振状态收到干扰,且散射过程复杂,涉及参数较多,不易于分析和量化。因此,本文考虑水下散射对偏振光的影响,提出一种简便、易于实现的偏振滤波算法,可通过优化方法得到成像效果最佳的偏振态区间,利用这个区间成像,从而起到抑制散射的作用,提高图像对比度,获得更清晰的成像。最优偏振度和偏振角成像区间可表示为:
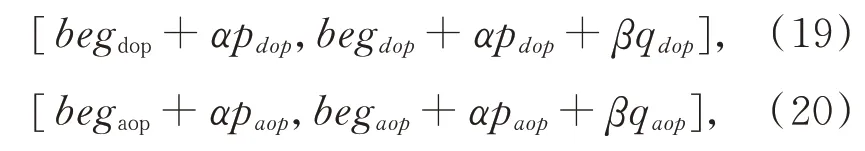
其中:α为区间步进系数,β为区间大小系数,beg为优化区间起点,p为偏振态的最优步进单位,q为偏振态的最小优化区间。
首先,为减少运算时间及保留图像细节,设定偏振度和偏振角的最优步进单位pdop=0.1,paop=20°,最小优化区间qdop=0.1,qaop=20°,优化区间起点begdop=0;begdop=-80°。然后,使用不同区间步进系数α和区间大小系数β的偏振态区间对图像进行偏振滤波,即偏振态在候选偏振态区间内的像素,其偏振态保持不变,区间外的像素使用周围八邻域的所有像素偏振态的中值替代。之后,将EME(Enhancement Measure Evaluation)[21-22]作为优化判定指标,筛选出偏振滤波后图像质量最佳即EME 最大的区间步进系数αoptimum和大小系数βoptimum,并带入公式(19)和公式(20),从而得到偏振态的最优成像区间。最后,使用最优成像区间对原偏振图像进行偏振滤波,可获得清晰图像即为去散射后的图像。偏振度的最优成像区间求解流程如图3 所示,偏振角类似。
图4 为特定偏振态的EME 值与区间步进系数α和区间大小系数β的关系,其中,图4(a)对应偏振度,图4(b)对应偏振角。由图可得,偏振度的αoptimum=2,βoptimum=8;偏振角的αoptimum=4,βoptimum=2。因此,偏振度的最优成像区间为0.2~1,偏振角最优成像区间为0°~40°。
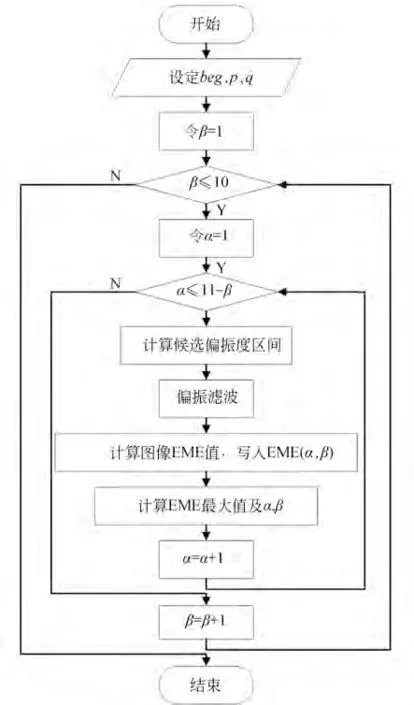
图3 偏振度最优成像区间求解流程Fig.3 The process of solving the optimal imaging interval of degree of polarization
3 实验装置与方法
实验装置及布局如图1 所示,主要包括偏振相机、玻璃水箱、偏振光源,成像目标,聚苯乙烯粉末。偏光相机的型号为PHX050S-P,目标分辨率为2 448×2 048,比特数为12,其采用焦平面偏光成像,镜头焦距为10.5 mm,可以一次拍摄四张偏振角度分别为0°,45°,90°和135°的线偏振光强度图像,如图2 所示。这种方式一次曝光即能通过公式(11)~公式(12)获得图像的偏振状态,适用于实时的动态偏振信息的探测,此处设定曝光时间为0.1 s。采用500 mm×250 mm×250 mm 的透明玻璃水箱作为容器,并在内侧的5个侧面上覆盖了黑色覆盖物,以避免环境光的干扰和水箱壁的反射。成像目标为金属罐,左侧有花纹纹理图像,图案鲜艳;右侧有文字图像,文字清晰,适用于水下的主观视觉质量评价。
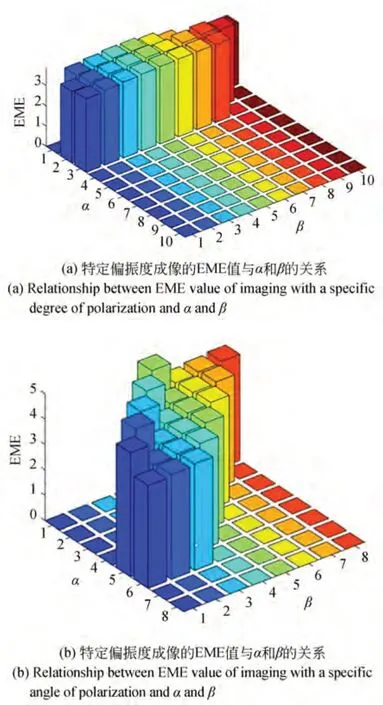
图4 特定偏振态成像的EME 值与α 和β 的关系Fig.4 Relationship between the EME value of imaging in a specific polarization state and α and β
将目标放置于装满纯净水的玻璃水缸,按图1 所示,进行装置的布局,然后进行灰度成像,获取清澈水下的目标光强图像之后,加入适量的聚苯乙烯粉末,进行浑水下的灰度成像、偏振成像,获取目标的光强图和偏振图像,并用本文的算法获取优化后的偏振图像。
4 实验结果
首先对实验结果进行主观视觉质量评价。实验结果如图3~图4 所示。图5(a)是清澈水体下的目标光强图像。由于水分子散射和吸收,其边缘模糊,光强度较低,但金属罐的纹理基本可见。图5(b)是浑浊水体中的目标光强图像,由于水下悬浮粒子强散射作用,相比于纯水中的目标光强图,其亮度很低,基本无法辨别金属罐的边缘轮廓,只能大致辨认出目标位置。

图5 清澈和浑浊水下目标光强图Fig.5 Target light intensity images under clear and turbid water
图6(a)是浑浊水体中的偏振度图像,与光强图比较,其成像效果大幅改善,边缘清晰,中间的黑白条纹清晰可见,罐头部突起的环和罐口都成像清晰,甚至连右侧的文字都能初步辨认。但由于后向散射的作用,使图像存在“帷幔效应”[6],导致对比度有所下降。图6(c)是浑浊水体中的偏振角图像,相比于光强图,其轮廓大致可见,但边缘模糊,中间的黑白条纹分界线不清晰,噪点也较多。
利用MATLAB 软件平台编制了优化算法来获取最佳的偏振度和偏振角阈值,进行偏振滤波,在此情况下,获取的偏振度的最优成像区间为0.2~1,偏振角最优成像区间为0°~40°。图6(b)是本文算法处理得到的优化偏振度图像,达到了较好的成像效果,相比于偏对比度显著提高。图6(d)是本文算法处理得到的优化偏振角图像,对比偏振角图像,其成像效果大幅改善振度图,其有效抑制了后向散射,右侧可辨认出字迹,图像,轮廓较为清晰,黑白条纹、顶部凸环和罐口均可见,甚至金属罐左侧的花纹纹理都依稀可见。
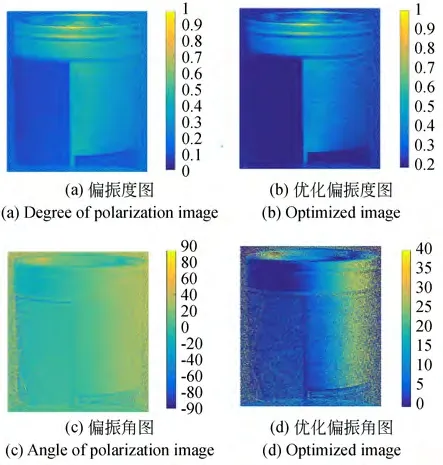
图6 浑浊水下图像处理结果Fig.6 Image processing results under turbid water
5 讨 论
根据实验结果,可知优化方法的偏振度和偏振角图像的可视效果较好。除了主观视觉质量评价外,本文也引入了无参考的图像质量评价方法,对水下图像进行客观评价。EME(Enhancement Measure Evaluation)[21-22]的物理意义是对图像局域灰度的变化程度的表现,局域灰度变化越强,图像表现出的细节越强,得到的EME 也越大。方差、平均梯度和均值,均为常见的评价指标,数值越大,代表图像的质量越好。表1 展示了浑水实验中不同图像在四种图像评价下的数值。图7 是光强、偏振与优化方法的图像评价指标对比柱状图,图像类别序号从a到e分别代表浑水环境下的强度图像、偏振度图像、偏振角图像、优化的偏振度图像和优化的偏振角图像。
综合以上4 种评价指标,基于特定偏振态成像的方法有更高的EME 值,尤其是优化后的偏振角图像,相比于处理前,提升的幅度达455%,这也对应了优化的偏振角图像良好的主观视觉效果。此外,优化偏振度、偏振角图像的方差相比优化前的值,提高了38% 和124%。优化偏振度、偏振角图像的平均梯度相比优化前的值,提高6% 和19%,均有较大幅度的提高。均值方面,对于优化后的偏振度和偏振角有一定程度下降,这是由于本文偏振滤波算法舍弃了部分认为是散射光的无效信息,但下降幅度不大,大概10%,且总体上提高了图像质量。
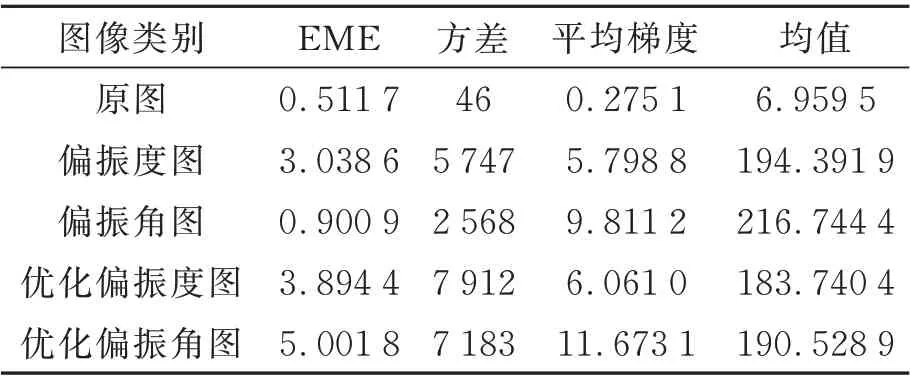
表1 图像质量对比Tab.1 Image quality comparison
从表1 和图7 的比较结果,充分说明本文方法能抑制水体散射,增加图像对比度,有效改善图像质量,尤其在浑浊水下环境,能显示出清水无法观察到的细节信息,比如优化偏振角图像能观察到金属罐左侧的花纹纹理,优化的偏振度图像能分辨右侧文字。此外,本文方法操作简便,易于实现,特别适用于浑浊水下实时探测。
6 结 论
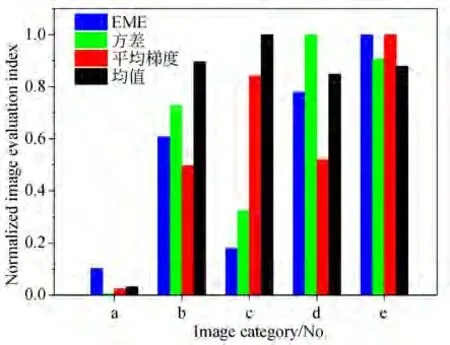
图7 光强、偏振与本文方法的图像评价指标对比Fig.7 Comparison of image evaluation indexes of light intensity,polarization,and our method
本文针对散射对水下偏振成像造成干扰的问题,通过建立水下偏振成像的物理模型,分析了水下散射对模型的影响,提出了一种自适应的基于特定偏振态的水下图像去散射方法。使用偏振相机进行浑浊水体的成像对比实验,并通过算法获得了去散射后的最优成像偏振态范围,在0°~40°的最优偏振角成像区间和0.2~1 的偏振度的最优成像区间下,获取目标图像。实验结果表明:目标图像的主观视觉质量显著提升,客观评价指标EME 值的提升幅度高达455%,方差相比优化前的值,提升了38%和124%,平均梯度则提升6%和19%。因此,本文方法能有效抑制浑浊水体的散射,增加图像对比度,改善图像质量。这项工作为以后的水下偏振图像恢复和增强提供了新思路。
未来的研究包括进行户外真实水下环境的成像实验,改进原有的方法,进一步提升鲁棒性和自适应能力,用于满足实际应用的需求。同时也将水下图像的恢复与增强扩展到水下视频,重点解决视频的处理效率和水下数据传输的丢包延迟问题,最后实现对水下目标的实时检测与跟踪。
