单位根模型的复合分位数自回归推断
2021-07-02庞天晓
徐 成,庞天晓
(浙江大学 数学科学学院,浙江杭州 310027)
§1 引言
许多经济学和金融学的文献指出:由于经济和金融中的随机变量通常具有非平稳性,因此很多经济时间序列数据用单位根模型或者近单位根模型来建模比较合适.在过去的几十年,单位根模型和近单位根模型一直受到许多学者的关注,见Dickey和Fuller[1],Phillips[2]以及Phillips和Magdalinos[3]等文献.在单位根模型中,自回归系数等于1,而近单位根模型中的自回归系数通常假设接近1,并随样本容量大小而变化.近单位根模型形式多样.例如,Phillips[2]假设自回归系数ρ=ρn=1-c/n,其中c是一个常数,n是样本容量,这个模型可看成是单位根模型的推广,它在平稳一阶自回归模型和单位根模型之间建立了一座桥梁;Phillips和Magdalinos[3]建议取ρ=ρn=1-c/kn,其中c/=0,而kn是满足kn=o(n)的一个发散到正无穷的正常数序列.当c >0时,这个模型在平稳一阶自回归模型和刚才的近单位根模型之间建立了一座桥梁;当c <0时,这个模型在单位根模型和爆炸模型(即自回归系数是大于1的常数)之间建立了一座桥梁.Phillips和Magdalinos[3]提出的这个模型在金融市场的泡沫现象的统计建模中有重要的应用,可用来描述泡沫的膨胀过程和破灭过程,见Phillips和Shi[4].对于此类非平稳自回归模型,参数估计和假设检验是学者关注的主要课题.本文关注单位根模型的估计问题.
有很多方法可以用来估计自回归系数,例如最小二乘法和极大似然法.但是,当模型误差不是高斯分布时,这些方法通常不够稳健.也就是说,当遇到具有异常值或重尾特征的数据时,这些估计方法不够稳健.因此,需要寻找一些稳健的估计方法.在这个研究方向上,许多学者提出了各种稳健估计方法,例如Knight[5]和Herce[6].Koenker和Xiao[7]提出了单位根模型的分位数自回归估计方法.分位数方法最先是由Koenker和Bassett[8]提出的,用于估计线性回归模型中的回归系数.与传统的最小二乘法相比,分位数方法研究因变量的各种条件分位数,而最小二乘法只研究因变量的条件平均趋势.在Koenker和Xiao[7]中,当模型误差偏离高斯条件时,分位数自回归估计方法在稳健性方面被证明是优于其他很多现有方法的.受这一发现的启发,Zhou和Lin[9]成功地将分位数自回归方法应用于Phillips和Magdalinos[3]提出的近单位根模型.值得注意的是,在Koenker和Xiao[7]和Zhou和Lin[9]中,他们都只使用了一个分位点.
显然,分位数回归方法只使用了样本的局部信息.若分位点选择不当,分位数估计可能有不理想的估计偏差和估计精度.Zou和Yuan[10]提出了复合分位数回归方法,他们建议在统计推断中使用多个分位点而不是一个分位点,这样就会有更多的样本信息被用来进行统计推断.Zou和Yuan[10]指出:当模型误差偏离高斯条件时,这个方法可以比最小二乘法好很多.实际上,通过数值模拟他们发现:复合分位数回归方法在估计偏差和估计精度方面具有很大的优势.根据Zou和Yuan[10]的建议,倪和傅[11]用复合分位数自回归方法估计了Phillips和Magdalinos[3]提出的近单位根模型中的自回归系数,通过模拟分析,他们发现:复合分位数自回归估计比分位数自回归估计有更小的估计偏差和更好的估计精度.本文的目的是使用复合分位数自回归方法估计单位根模型中的自回归系数.
本文结构如下.§2提出单位根模型的复合分位数自回归估计,并研究此估计量的大样本性质.§3通过Monte Carlo模拟评估复合分位数自回归估计在有限样本情形下的表现.§4给出了一个实证分析.§5对该文进行了总结.单位根模型的复合分位数自回归估计的渐近理论的证明放在§6.§7研究了增广的Dickey-Fuller模型(ADF模型),并讨论了该模型中的复合分位数自回归估计的渐近理论.
§2 模型和结论
首先介绍本文接下来需要用到的一些记号.“⇒”表示概率测度弱收敛,“ p-→”表示依概率收敛,“ d-→”表示依分布收敛,“[nr]”表示nr的整数部分,“:=”和“=:”表示等价定义,上标“T”表示向量或矩阵的转置,“I(·)”表示示性函数.除非另有说明,本文中的极限均理解为n →∞.
设{yt,t ≥0}来自一阶自回归时间序列模型:

其中,{ut,t ≥1}是模型误差.在这个模型中,当α1=1时,(1)就是一个单位根模型.把由{us,s ≤t}生成的σ-域记为Ft,设0<τ1<τ2<……·<τK <1为K个分位点,其中K ∈N.记ut的τk-条件分位数为Qu(τk),并记yt对于Ft-1的τk-条件分位数为Qyt(τk|Ft-1).那么,下式成立:

记α0(τk)=Qu(τk),k=1,……,K.则(α0(τ1),……,α0(τK),α1)的复合分位数自回归估计定义为
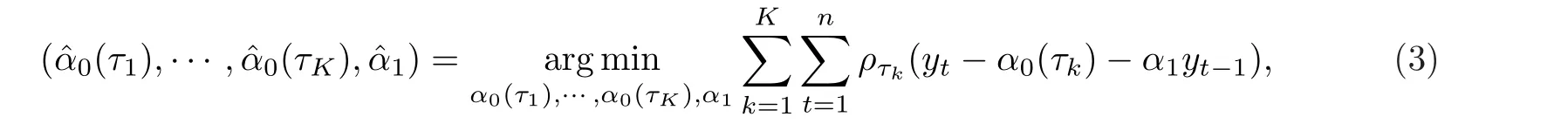
其中,ρτk(u)=u(τk-I(u <0)).
本文关注α1=1时的统计推断.考虑到金融时间序列数据普遍具有重尾的性质,与Zhou和Lin[9]以及倪和傅[11]一样,本文假设{ut,t ≥1}是一属于正态吸引场的独立同分布(i.i.d.)随机变量序列.对于模型(1),作如下两个假设.
· 假设1是一属于正态吸引场的i.i.d.随机变量序列,均值为0,方差可能无穷大.

在假设1中,由于{ut,t ≥1}的方差可能不存在,引入截尾的技巧.令
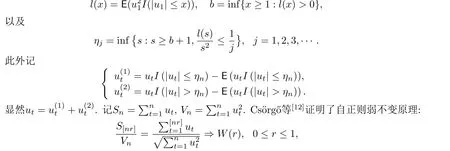
其中{W(r),0≤r ≤1}是一个标准维纳过程.根据Cs¨org˝o等[12]的式子(18),有


的部分和服从弱不变原理(参见Phillips和Durlauf[16]的Corollary 2.2):

结合(5)和(6),得

然后,根据Hansen[17]的Theorem 2.1,得

注1.由(6),(·)是一个布朗运动,且

2.根据Zou和Yuan[10]的建议,在实际应用中,为了方便起见可以等间隔地选取分位点,即取τk=k/(K+1).对于这样的取法,通过一些简单的计算,可知

下面的定理给出了模型(1)中α1的复合分位数自回归估计的收敛速度和极限分布.
定理2.1假设{yt,t ≥1}来自模型(1),其中α1=1.若假设1和2被满足,那么有

推论2.1假设{yt,t ≥1}来自模型(1),其中α1=1.若假设1和2被满足,那么有

在假设1中并未要求{ut,t ≥1}的方差一定存在.若{ut,t ≥1}的方差存在,则有以下推论:
推论2.2假设{yt,t ≥1}来自模型(1),其中α1=1.若假设1和2被满足,且0<Var(ut)=σ2<∞,那么有

注 若K=1时,即只使用一个分位点,不妨记为τ,那么由推论2.2可得
这正是Koenker和Xiao[7]里的结论.
接下来,研究α1的复合分位数自回归估计与分位数自回归估计的渐近相对有效性.只需计算如下的比值大小:


若上述比值大于1,则说明复合分位数自回归估计在估计有效性方面优于分位数自回归估计.为了便于计算,假设ut~N(0,1),τ=0.5(相应的分位数估计就是常见的最小绝对偏差估计),并取τk=k/(K+1).在这种情况下,根据Zou和Yuan[10]的Theorem 3.1,有

若取ut~t(3),τ=0.5,根据Zou和Yuan[10]的Corollary 3.1,经过一些简单的计算可得
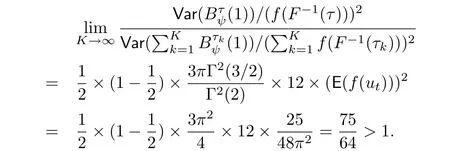
在实际中,需要选择合适的K值.根据(10)式以及参考Zou和Yuan[10]中关于渐近有效性的讨论(该文中第三章节),对于不同的K值,把的方差,即

的大小列于表1(该值越小,意味着复合分位数方法越有效),其中,ut=∈t-E(∈t),∈t来自以下7个分布:N(0,1),N(0,10),t(2),t(3),F(4,4),χ2(20),Beta(0.5,0.5).在ut的7个分布中,既有轻尾分布,也有重尾分布、非对称分布.从表1可以看出,总的来说,K越大,复合分位数估计方法的表现将会越好.

表1 具体数值比较
在实际中,还需要考虑估计方法的计算成本.在本模型中,考虑不同的K值所对应的估计方法所需的计算时间.通过R软件中的proc.time来提取计算时间.取ut~N(0,1),样本容量取为200,模拟的重复次数取为10000,将计算时间列于表2(在该表中,LS表示最小二乘法,QAR表示分位数自回归方法,CQARK表示采用K个分位点的复合分位数自回归方法).若实际工作者除了考虑估计有效性,还在乎计算成本,那么可对表1和表2进行综合分析,选择K值.若选择K=19,此时均匀的分位点分别是5%,10%,15%,……·,95%.

表2 不同K值的平均计算时间
§3 模拟
在本节中,通过Monte Carlo实验比较α1(其真值为1)的复合分位数自回归估计、分位数自回归估计以及最小二乘估计在有限样本情形下的表现.此外,将通过假设模型误差为N(0,1)或t(2)来分析α1的复合分位数自回归估计的有限样本分布与极限分布的吻合程度.其中,N(0,1)具有有限方差,而t(2)的方差不存在.
记α1的K-复合分位数估计为,同时记α1的最小二乘估计和分位数自回归估计为.根据定理2.1,α1的复合分位数自回归估计的极限分布由下式刻画:

根据Hamilton[18]以及Koenker和Xiao[7]中的结论,的极限分布分别由

为了简单起见,以下Monte Carlo实验的复合分位点都是均匀取值(即取为τk=k/(K+1),k=1,……,K),y0取为0;{ut,t ≥1}由ut=∈t -E(∈t)产生,其中∈t分别取为N(0,1),t(2),F(4,4),χ2(20),Beta(0.5,0.5)分布.对于分位数自回归估计,只考虑τ=0.25,0.5,0.75的三种情况.而对于复合分位数自回归估计,考虑K ∈{2,5,9,19,49}这些情形.在以下所有的实验里,样本容量n取为200,模拟的重复次数取为N=10000.
用QARτ表示取τ分位点的分位数自回归估计,CQARK的含义前面已给出说明.表3给出了三种估计方法在有限样本情形下的表现,括号内的数字表示均方误差.从表中可以看出:(1)当误差分布是正态分布时,最小二乘法在估计偏差和估计精度方面都具有最佳的有限样本表现.这是因为在正态情形下,最小二乘估计就是极大似然估计.(2) 无论模型误差是重尾分布还是非对称分布,复合分位数自回归方法在估计偏差和估计精度方面都优于最小二乘法.(3) 总的来说,当误差分布是非对称分布时,复合分位数自回归方法比分位数自回归方法更加稳健.(4) 总的来说,对于复合分位数自回归方法,当分位点个数K增大时,复合分位数自回归估计的有限样本表现越来越好.总之,当模型误差偏离高斯条件时,复合分位数自回归估计方法在估计偏差和估计精度方面要优于最小二乘法和分位数自回归方法.

表3 不同误差分布假设下, α1的各种估计量在有限样本情形下的表现
接下来假设模型误差为N(0,1)或t(2),然后比较的有限样本分布与极限分布的吻合程度.由定理2.1知
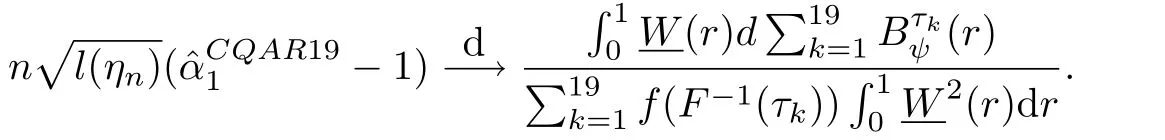
考虑到t(2)的方差不存在,采用推论2.1的表达式:

然后分析统计量Υn的有限样本分布与它的极限分布的吻合程度.取样本容量n=200,模拟重复次数为100000次.图1和图2分别给出了当模型误差为N(0,1)和t(2)时Υn的有限样本分布与极限分布.从这两张图中可以看出:(1) Υn的有限样本分布与极限分布是非常吻合的;(2) 类似于最小二乘估计,复合分位数自回归估计(经过规范化后)的极限分布是左偏的.
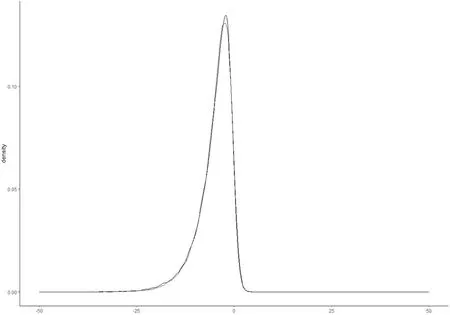
图1 模型误差为N(0,1)时Υn的有限样本分布(实线)与极限分布(虚线)

图2 模型误差为t(2)时Υn的有限样本分布(实线)与极限分布(虚线)
§4 实证分析
从美国商务部经济统计局(BEA)下载了美国从1947年第1季度到2008年第4季度的季度GDP数据(单位:亿美元).考虑季度GDP数据的对数序列.如图3所示,该序列表现出上升趋势,图4给出了一阶差分序列的时序图,该差分序列看起来在一个固定的水平附近波动.为了证实所观测到的现象,对该对数序列进行了增广的Dickey-Fuller单位根检验(相应的模型见(22)),当q=1时,检验统计量(见Hamilton[18],第523-524页)的样本值为-1.36364,相应的p值为0.5489,因此在0.05的显著水平下,单位根假设不能被拒绝.还选取了一些不同的q值(包括q=0,此时对应于普通的单位根模型),都没有改变假设检验的结论(q=0时,p值为0.3634).
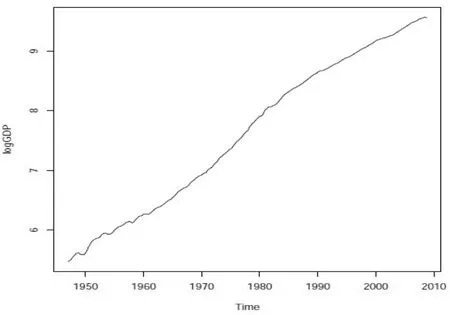
图3 对数GDP序列的时序图

图4 对数GDP一阶差分序列的时序图
因此,可以假设该对数GDP序列来自普通的单位根模型或者增广的Dickey-Fuller模型.不妨假设该数据来自普通的单位根模型:yt=α1yt-1+ut,α1=1.对于该样本数据,分别用最小二乘法,分位数自回归估计方法和复合分位数自回归估计方法对参数α1进行统计推断.对于分位数自回归估计,考虑τ=0.25,0.50,0.75的三种情况.而对于复合分位数自回归估计,选取K ∈{2,5,9,19}这4种情形.在获得参数α1的估计量后,用来比较各个模型的均方误差的大小,其中yt为真值,为模型拟合值,样本容量T=248.计算结果见表4.可以发现估计值都比较接近1,而复合分位数自回归估计方法的均方误差要普遍小于最小二乘估计和分位数估计的均方误差.这意味着,从数据与模型的吻合度考虑,复合分位数自回归估计方法具有一定的优势.

表4 不同估计方法的表现
§5 结论
本文利用Zou和Yuan[10]提出的复合分位数估计方法研究了单位根模型中的自回归系数的统计推断.得到了复合分位数自回归估计的渐近性质,并通过Monte Carlo模拟比较了复合分位数自回归估计与最小二乘估计和分位数自回归估计在有限样本情形下的表现.模拟结果表明,当模型误差偏离高斯条件时,复合分位数自回归估计在估计偏差和估计精度方面都要优于最小二乘估计和分位数自回归估计.此外,分析了美国季度GDP数据的对数序列,分析表明:从数据与模型的吻合度考虑,用复合分位数估计方法进行统计推断是合适且具有一定优势的.
§6 证 明
在本节中,将给出定理2.1的证明.首先,给出一个引理.
引理6.1设yt由模型(1)生成,其中α1=1.在假设1的条件下,有:


由正态吸引场随机变量的泛函中心极限定理,

定理2.1的证明下面这个恒等式(参考Knight[5])在证明中扮演重要的作用:

应用等式(11)可得

接下来,分别处理等式(12)中等号右侧的各项.
首先考虑(12)中等号右侧的前两项.注意到(6)和(8)联合成立,于是应用Hansen[17]的Theorem 2.1,可得


注意到v1,v2是事先取定的有限值,所以根据引理6.1,对于任意的1≤k ≤K,
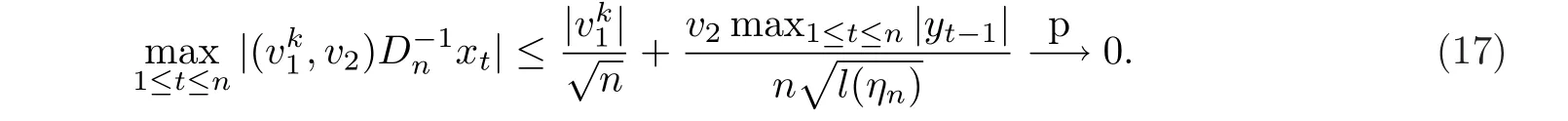
因为K是固定的,所以

因此利用假设2和(15),有

将(14),(16)以及(18)结合在一起,可得
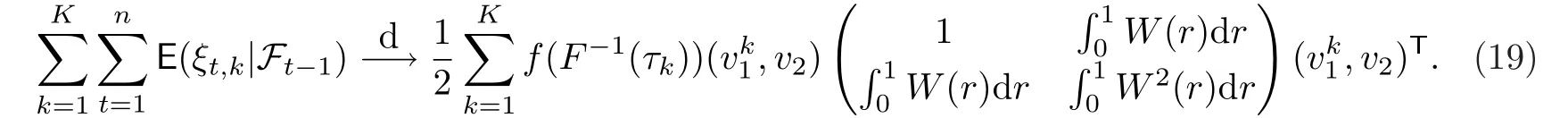
检查以上的证明过程,可以发现下式也成立:


不难看出(13),(19)和(21)是联合收敛的.于是

经过简单的计算,可知Z的极小值点为

那么,根据Knight[14]的Lemma A,可得

§7 推 广
7.1 模型与渐近理论
在本节中,将模型(1)推广至Dickey和Fuller[1]提出的增广的Dickey-Fuller模型(ADF模型),并研究此模型的复合分位数自回归估计的渐近理论.ADF模型表述如下:

其中,α1=1,Δ是差分算子,L是滞后算子,ut是模型误差.
对ADF模型(22),作如下的两个假设.
· 假设1’的根都在单位圆外,是一个属于正态吸引场的i.i.d.随机变量序列,均值为0,方差可能无穷大.
· 假设2’{ut,t ≥1}的分布函数F(·)有连续的Lebesgue密度函数f(·),且在集合{x:0<F(x)<1}上满足0<f(x)<∞.此外,假设supx∈R|f′(x)|<∞.
那么,yt关于Ft-1的τk-条件分位数为
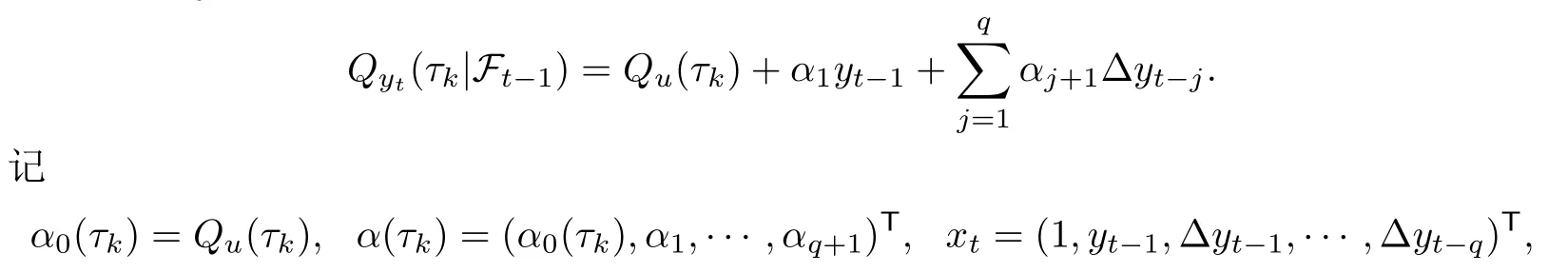
容易看出

把(α0(τ1),……,α0(τK),α1,……,αq+1)的复合分位数自回归估计定义为
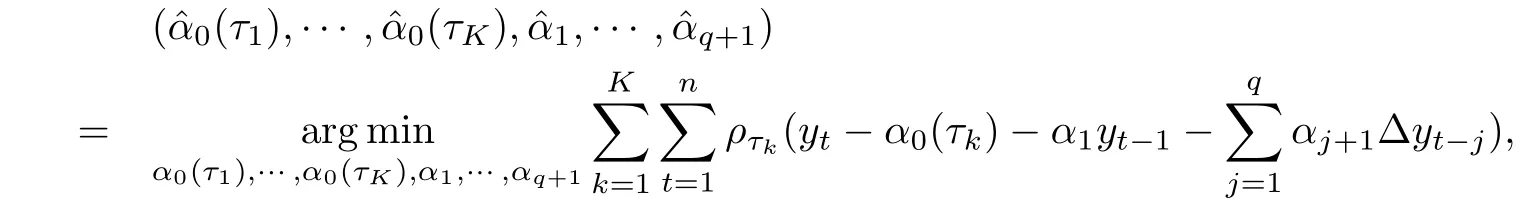
其中ρτk(u)=u(τk-I(u <0)).

那么,容易看出
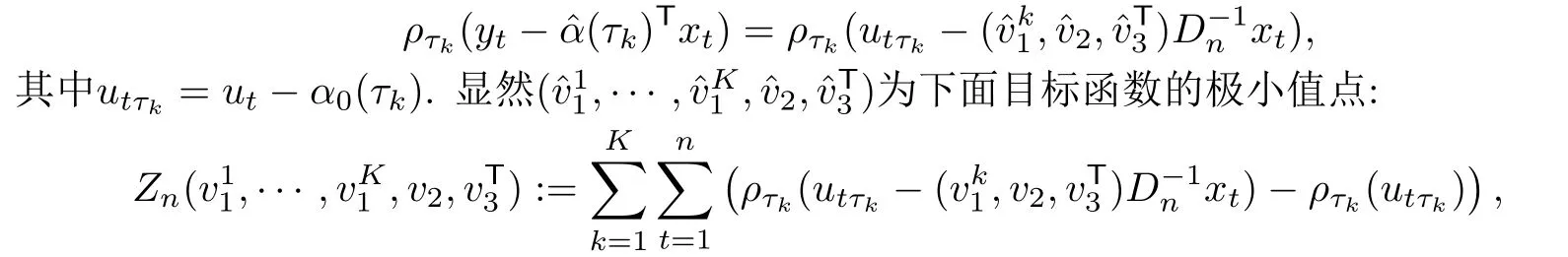
为了记号简便,记

及ψτk(u)=τk-I(u <0).容易看出,由假设1’,{∈t,t ≥1}是来自正态吸引场的平稳AR(p)过程,但它的方差可能不存在.因此对它应用截尾技巧:

类似于(7)的推导,通过上述的截尾技巧和Phillips和Durlauf[16]的Corollary 2.2,可得

那么,对于模型(22),有如下的渐近理论:
定理7.1假设{yt,t ≥1}来自模型(22),其中α1=1.若假设1’和2’被满足,那么有
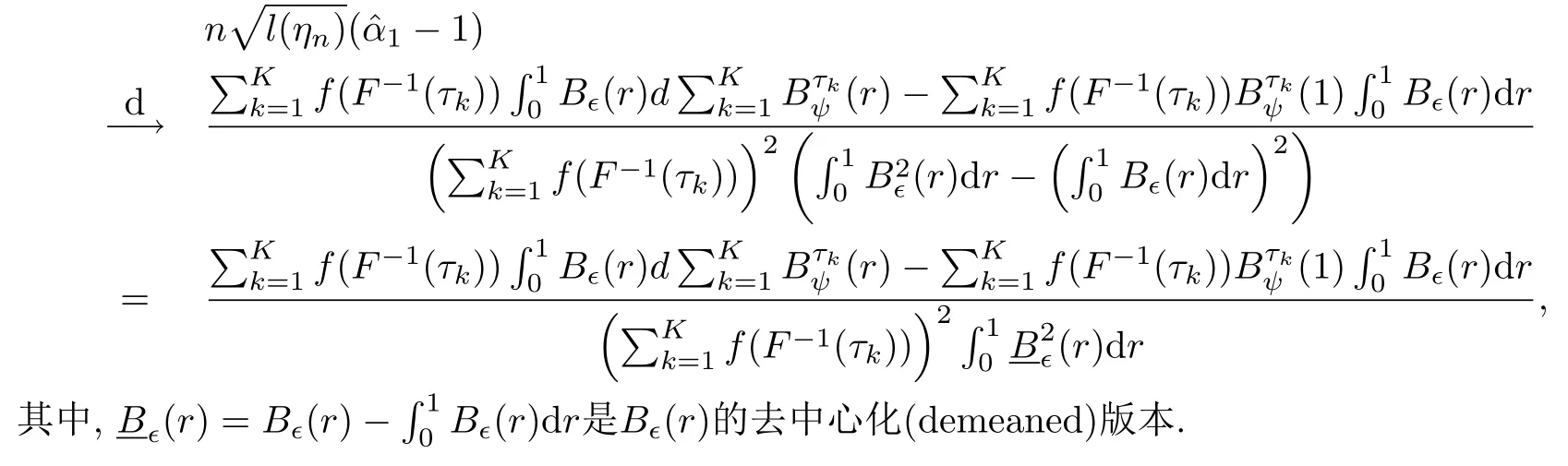
7.2 证明


接下来分别处理等式(25)右边的四项.
对于等式(25)右边的第一项,直接应用结论(24)可得
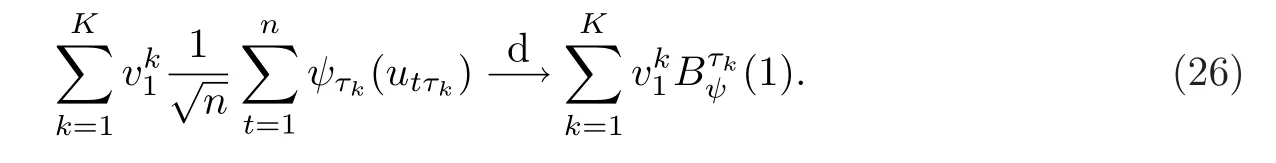
对于等式(25)右边的第二项,只需研究

对于(27),注意到

且y0在渐近分析中不起作用.因此根据(24)和Hansen[17]的Theorem 2.1,有

容易看出,(26)和(29)是联合收敛的.对于(28),先定义

然后将证明随机向量(28)依分布收敛于一个多元正态随机向量,即

要证结论(31),根据Cram´er-Wold方法,只需证:对任意的非零q维常数列向量a=(a1,……,aq)T,
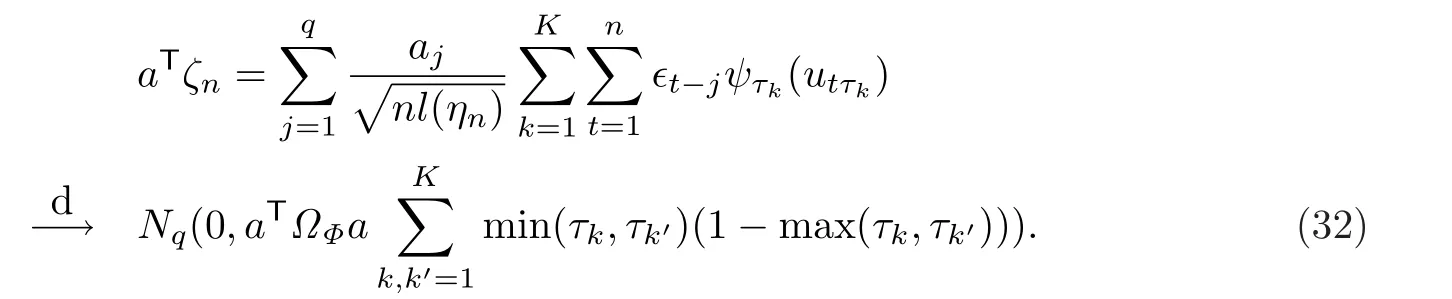
显然,E(aTζn)=0.接下来,把aTζn分解成两部分:

不难知道等式(33)右边的第二项相对于第一项是可忽略的.所以,只需证明等式(33)右边的第一项有正态的极限分布.记

显然mnt关于Ft是一个鞅差序列,且

在上式中利用了(30)中的定义.因此根据鞅中心极限定理,要证明(32)成立,只需验证下面的Lindeberg条件成立即可.对任意给定的δ >0,

接下来就来验证它.首先来证明

对任意的θ >0,利用Cs¨org˝o等[12]中的Lemma 1,有

所以(35)成立.容易看出(35)可推出

进一步地,注意到|ψτk(utτk)|≤2,有


这意味着




这意味着

结合(37),(39)和(40),可得

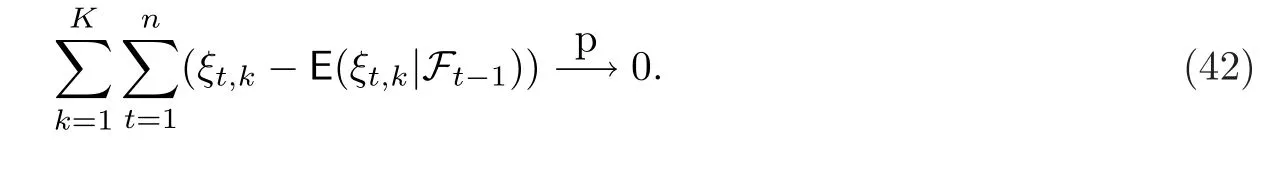
现在,结合(25),(26),(36),(41)和(42)(并注意到(26),(36),(41)和(42)是联合收敛的),可得
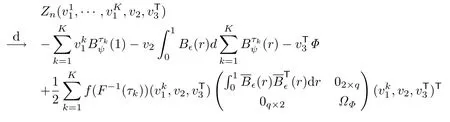


那么根据Knight[14]的Lemma A,可得

