双hypergenic函数向量的带Haseman位移带共轭的边值问题

刘利霞,杜晓静,谢永红

(河北师范大学 数学科学学院,河北石家庄 050024)

§1 引言

Clifford代数是Clifford[1]在1878年建立的可结合但不可交换的代数,它在物理上有很重要的应用[2].1982年,Brackx[3]等建立了Clifford分析的理论基础.近年来Clifford分析发展迅速,Eriksson[4-6],黄沙[7-9],任广斌[10-11],乔玉英[12],谢永红[13-18]和杨贺菊[19-21]等在Clifford分析中做了大量的工作.

1996年,黄沙[8]研究解决了Clifford分析中双正则函数的非线性边值问题.1998年,黄沙等[9]研究了Clifford分析中多个未知函数向量的非线性边值问题.2001年,谢永红,黄沙和乔玉英[18]研究了广义双正则函数的带共轭值带位移的边值问题.2005年,乔玉英[12]研究了超正则函数的边值问题.2009年,Eriksson和Orelma[4]给出了实Clifford代数Cln+1,0(R)中hypergenic函数的Cauchy积分公式.2014年,谢永红[13-14]研究了对偶的k-hypergenic函数的Cauchy积分公式以及hypergenic拟Cauchy型积分的边界性质,给出了Plemelj公式与Privalov定理.2017年,李冲[22]等研究了hypergenic函数的边值问题.2018年,张贵玲[23]等研究了hypergenic函数向量的边值问题.2019年,陈雪[24-25]等研究了双hypergenic函数的Cauchy积分公式及其相关理论.

本文在以上基础上研究双hypergenic函数向量的带Haseman位移带共轭的边值问题解的存在性和线性边值问题解的存在唯一性，并给出解的积分表达式,推广了文献[22-25]的一些结果.

§2 预备知识

见文献[4],设Cln+1,0(R)是实Clifford代数,其中n为自然数,单位元是e∅=1,其基元素是e0,e1,……,en;e0e1,……,en-1en;……·;e0e1……·en,且

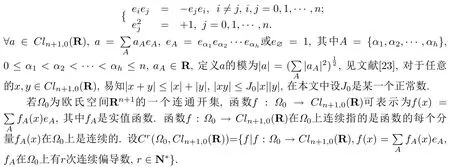
定义2.1[5]对于任意的a,b ∈Cln+1,0(R),定义两种运算:

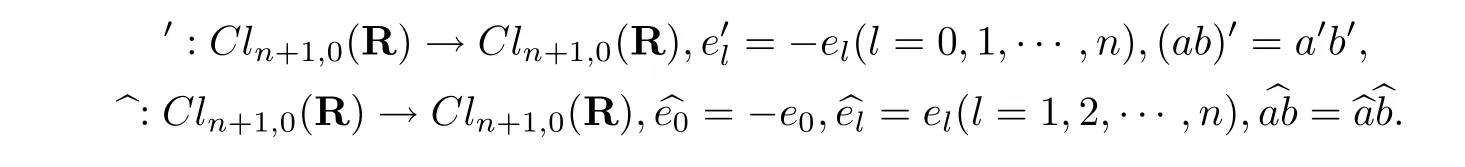
且定义两种映射:

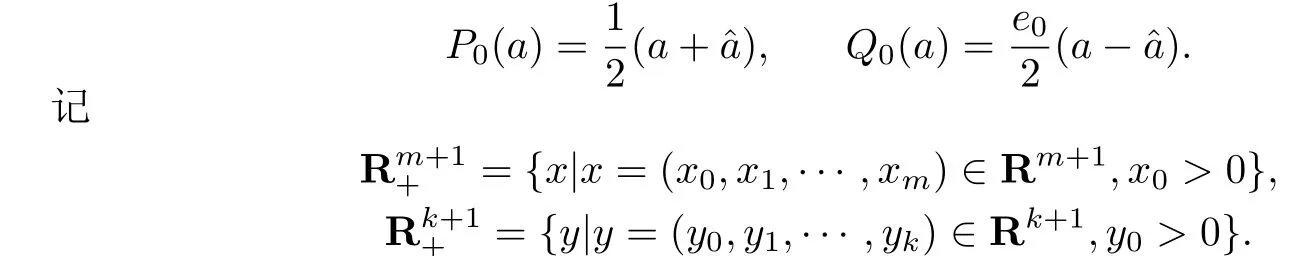
在本文中设Ω=Ω1×Ω2为欧氏空间(1≤m ≤n,1≤k ≤n)中的一个连通开集,且Ωi的边界∂Ωi(i=1,2)均为光滑,紧致,可定向的Liapunov曲面.

对于任意的∀x ∈Rm+1,y ∈Rk+1,称F(x,y)=(f1(x,y),f2(x,y),……,fp(x,y)),G(x,y)=(g1(x,y),g2(x,y),……,gp(x,y))(其中fi(x,y),gi(x,y)∈Cr(Ω,Clm+k+2,0(R)),i=1,2,……,p,r ≥1)是定义在Ω上的函数向量,现定义函数向量的加法和乘法如下:

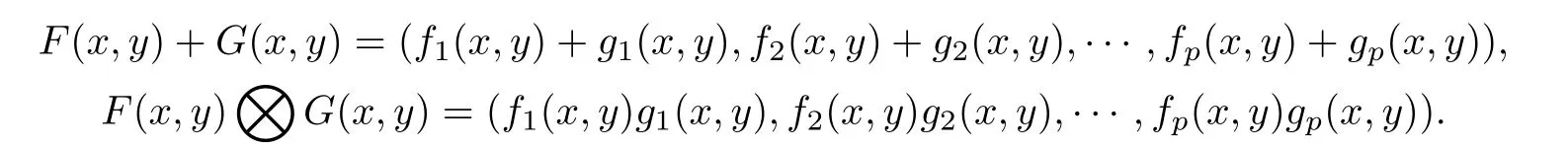
若函数l(x,y)∈Clm+k+2,0(R),则定义

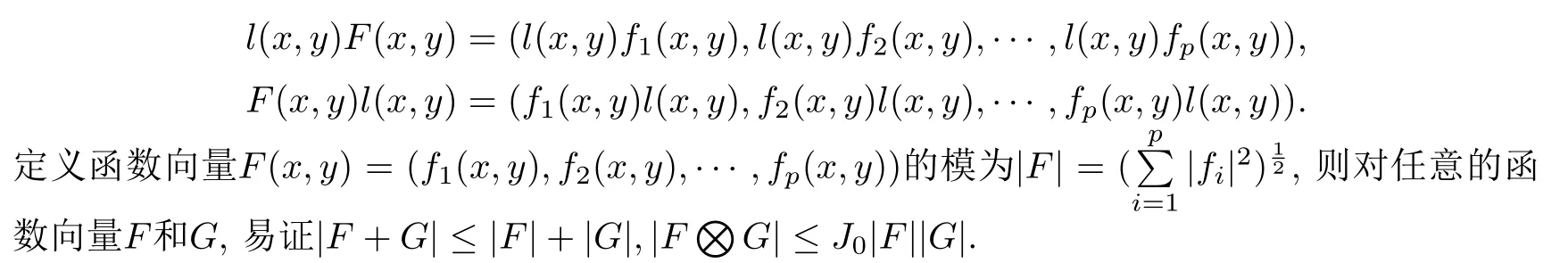
定义2.2[23]设函数向量F(x,y)=(f1(x,y),f2(x,y),……,fp(x,y)).对于固定i(i=1,2,……,p),若存在一个正常数M,使得对任意的(x1,y1),(x2,y2)∈∂Ω1×∂Ω2,有|fi(x1,y1)-fi(x2,y2)|≤M|(x1,y1)-(x2,y2)|β,其中0＜ β ＜1,则称函数fi在∂Ω1× ∂Ω2上是H¨older连续的.现用H(∂Ω1×∂Ω2,β,Clm+k+2,0(R))代表定义在∂Ω1×∂Ω2上,取值在Clm+k+2,0(R)中的H¨older连续函数的全体.函数向量F(x,y)在∂Ω1×∂Ω2上H¨older连续指它的每个分量fi(i=1,2,……,p)在∂Ω1×∂Ω2上是H¨older连续的.现用Hp(∂Ω1×∂Ω2,β,Clm+k+2,0(R))代表定义在∂Ω1×∂Ω2上,取值在Clm+k+2,0(R)中的H¨older连续函数向量的全体.

对于任意的函数向量F(x,y)∈Hp(∂Ω1×∂Ω2,β,Clm+k+2,0(R)),定义其范数为

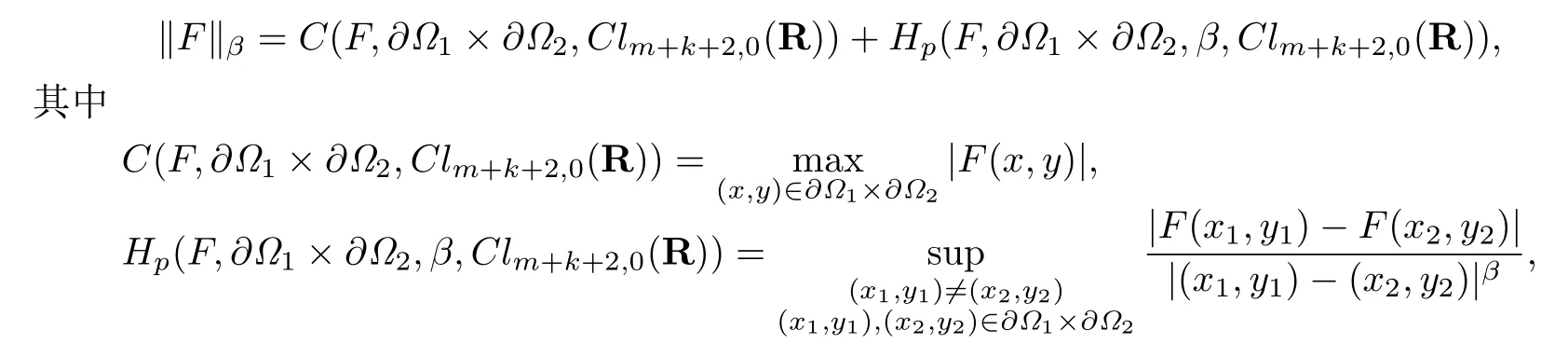
易知Hp(∂Ω1×∂Ω2,β,Clm+k+2,0(R))是一个Banach空间,且对于任意的函数向量F,G ∈Hp(∂Ω1×∂Ω2,β,Clm+k+2,0(R)),有

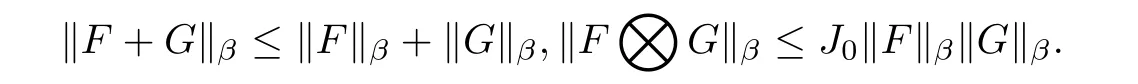
定义2.3设函数向量F(x,y)=(f1(x,y),f2(x,y),……,fp(x,y)),其中fi(x,y)∈Cr(Ω,Clm+k+2,0(R)),i=1,2,……,p,r ≥1,若fi(x,y)(i=1,2,……,p)满足:

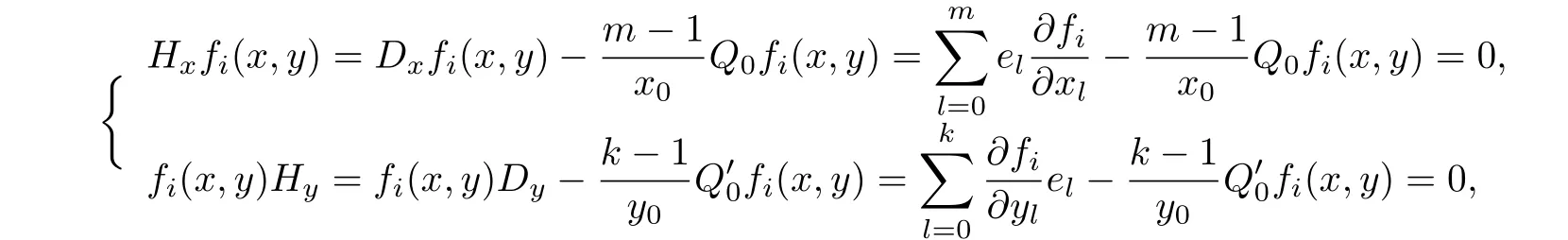
则称F(x,y)在Ω上关于x是左(m-1)-hypergenic函数向量,且关于y是右(k-1)-hypergenic函数向量;或称F(x,y)在Ω上是双hypergenic函数向量.

引理2.1[25](双hypergenic函数的Cauchy积分公式) 设区域,且Ω1,Ω2分别是中的m+1,k+1维链,.若φ(x,y)是U1×U2上的双hypergenic函数,则对任意的(x,y)∈Ω1×Ω2,有

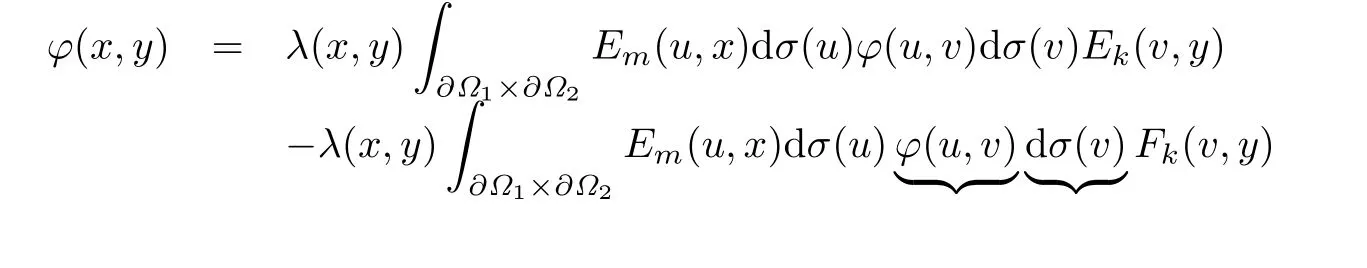
定义2.4若函数向量Φ(x,y)=(φ1(x,y),φ2(x,y),……,φp(x,y))∈Hp(∂Ω1×∂Ω2,β,Clm+k+2,0(R)),,则称

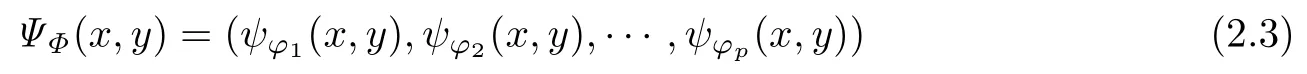
为双hypergenic拟Cauchy型积分向量,其中

定义2.5若函数向量Φ(t1,t2)=(φ1(t1,t2),φ2(t1,t2),……,φp(t1,t2))∈Hp(∂Ω1×∂Ω2,β,Clm+k+2,0(R)),(t1,t2)∈∂Ω1×∂Ω2,i=1,2,……,p,若

引理2.4[25](双hypergenic函数的Plemelj公式) 若函数φ ∈H(∂Ω1×∂Ω2,β,Clm+k+2,0(R)),

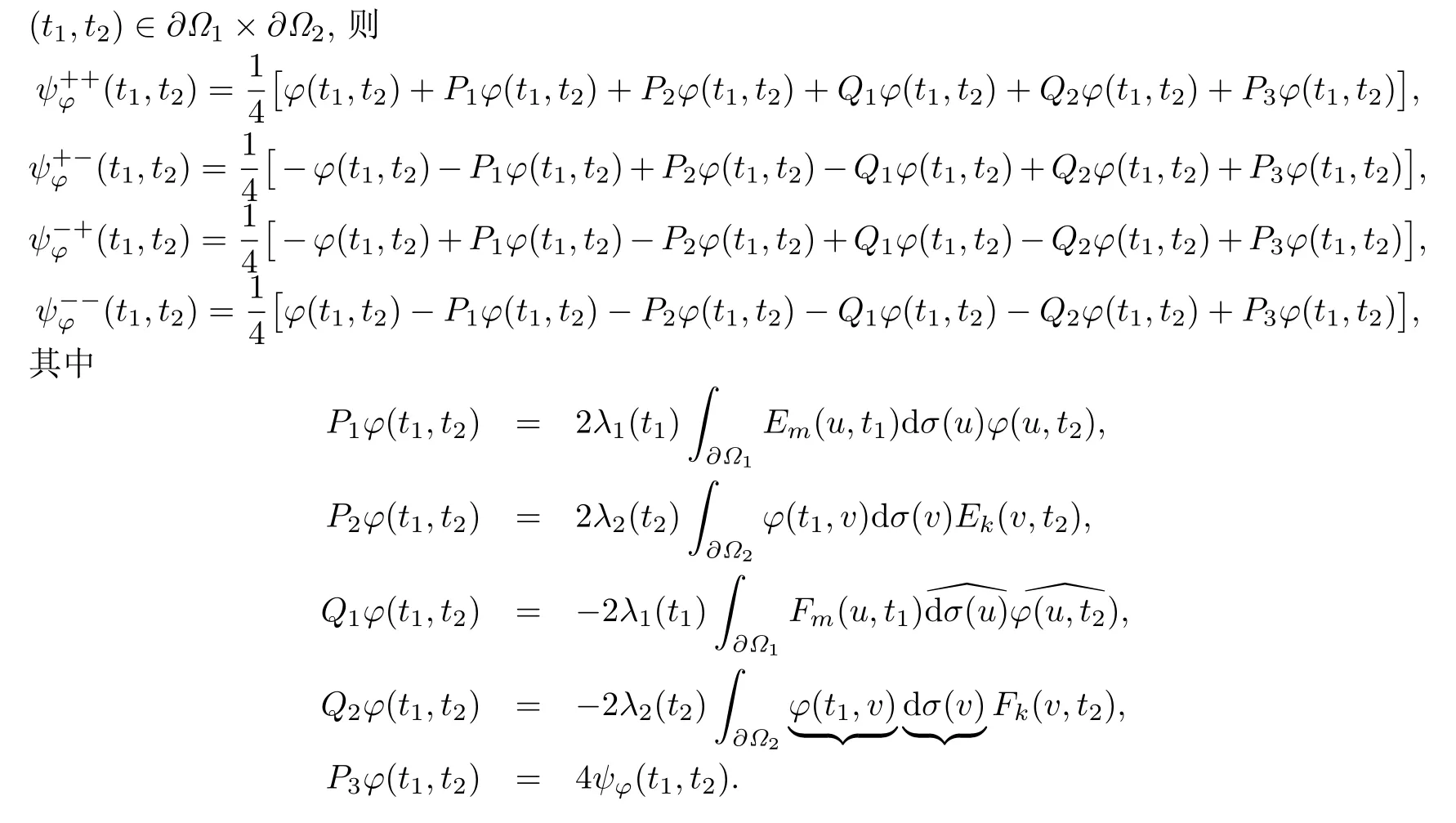
推论2.4(双hypergenic函数向量的Plemelj公式) 若函数向量

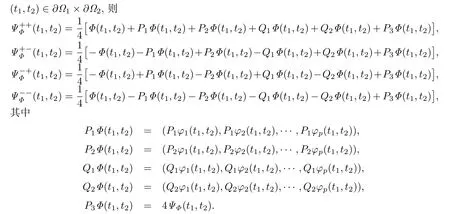
定义2.6[18]若d(t1,t2)=(d1(t1),d2(t2)),di为∂Ωi →∂Ωi(i=1,2)上的同胚映射,则称d(t1,t2)为∂Ω1×∂Ω2上的Haseman位移.

其中J2是一个与Φ无关的正常数.

由引理2.5和推论2.6知下面的推论成立.

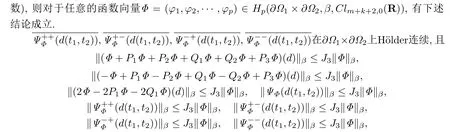
其中J3是一个与Φ无关的正常数.

§3 双hypergenic函数向量的带Haseman位移带共轭的边值问题

设函数向量Aj(t1,t2),Bj(t1,t2),Cj(t1,t2),Dj(t1,t2),G(t1,t2)∈Hp(∂Ω1×∂Ω2,β,Clm+k+2,0(R))(j=1,2),本文寻求在上的双hypergenic函数向量(x,y),其满足在∂Ω1× ∂Ω2上H¨older连续,且,并且满足带Haseman位移带共轭的边值条件:

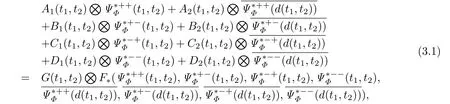
其中Aj=(aj1,aj2,……,ajp),Bj=(bj1,bj2,……,bjp),Cj=(cj1,cj2,……,cjp),Dj=(dj1,dj2,……,djp),G=(g1,g2,……,gp),F*=(f1,f2,……,fp),(t1,t2)∈∂Ω1×∂Ω2,j=1,2,称上述问题为双hypergenic函数向量的带Haseman位移带共轭的边值问题,简称N问题.特别地,当F* ≡(1,1,……,1)时,上述问题称为双hypergenic函数向量的带Haseman位移带共轭的线性边值问题,简称L问题.

由推论2.2知ΨΦ在上是双hypergenic函数向量,由推论2.6知ΨΦ在∂Ω1×∂Ω2上是H¨older连续的,由推论2.3知ΨΦ(x,∞)=ΨΦ(∞,y)=ΨΦ(∞,∞)=0.将双hypergenic函数向量的Plemelj公式代入(3.1)式,则N问题可以转化为求解奇异积分方程

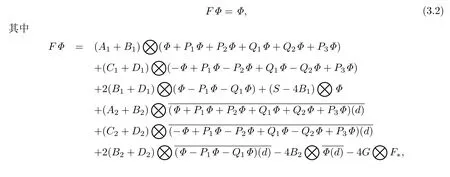
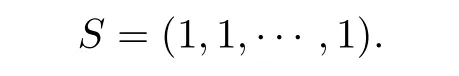
其中J4,J5,……,J11为与t1,t2和Φ无关的正常数.F*(0,0,0,0,0,0,0,0)=0,Aj(t1,t2),Bj(t1,t2),Cj(t1,t2),Dj(t1,t2)满足条件:

证令T={Φ|Φ=(φ1,φ2,……,φp)∈Hp(∂Ω1×∂Ω2,β,Clm+k+2,0(R)),‖Φ‖β ≤M,M为某一个正常数}.

先证F是自身到自身的映射,即证对于任意的Φ ∈T,有FΦ ∈T.

任意的Φ ∈T,由函数向量的性质,推论2.6 和推论2.7可得

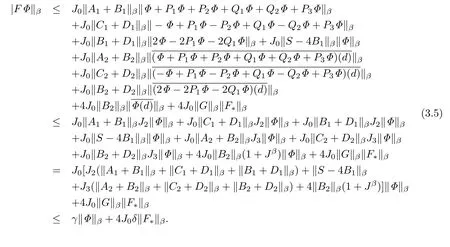
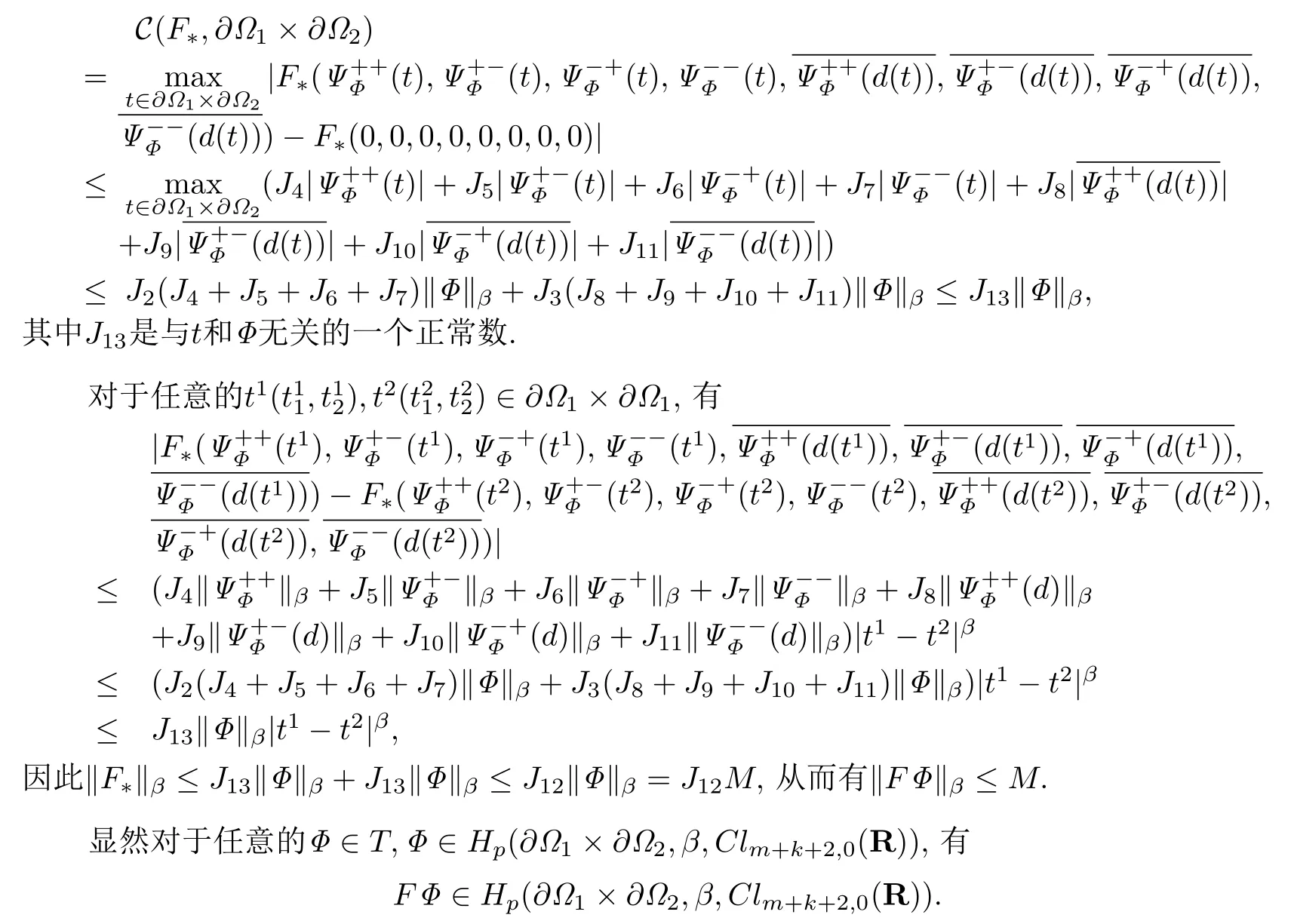
所以FΦ ∈T.因此F是自身到自身的映射.

下面证明F是一个连续映射.

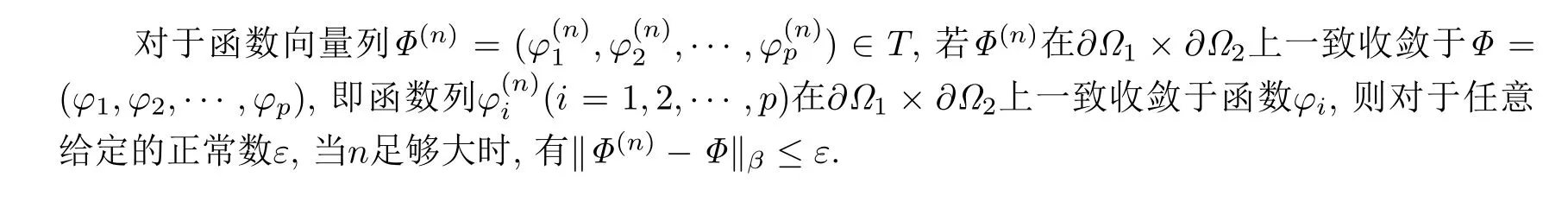
由推论2.6和推论2.7知

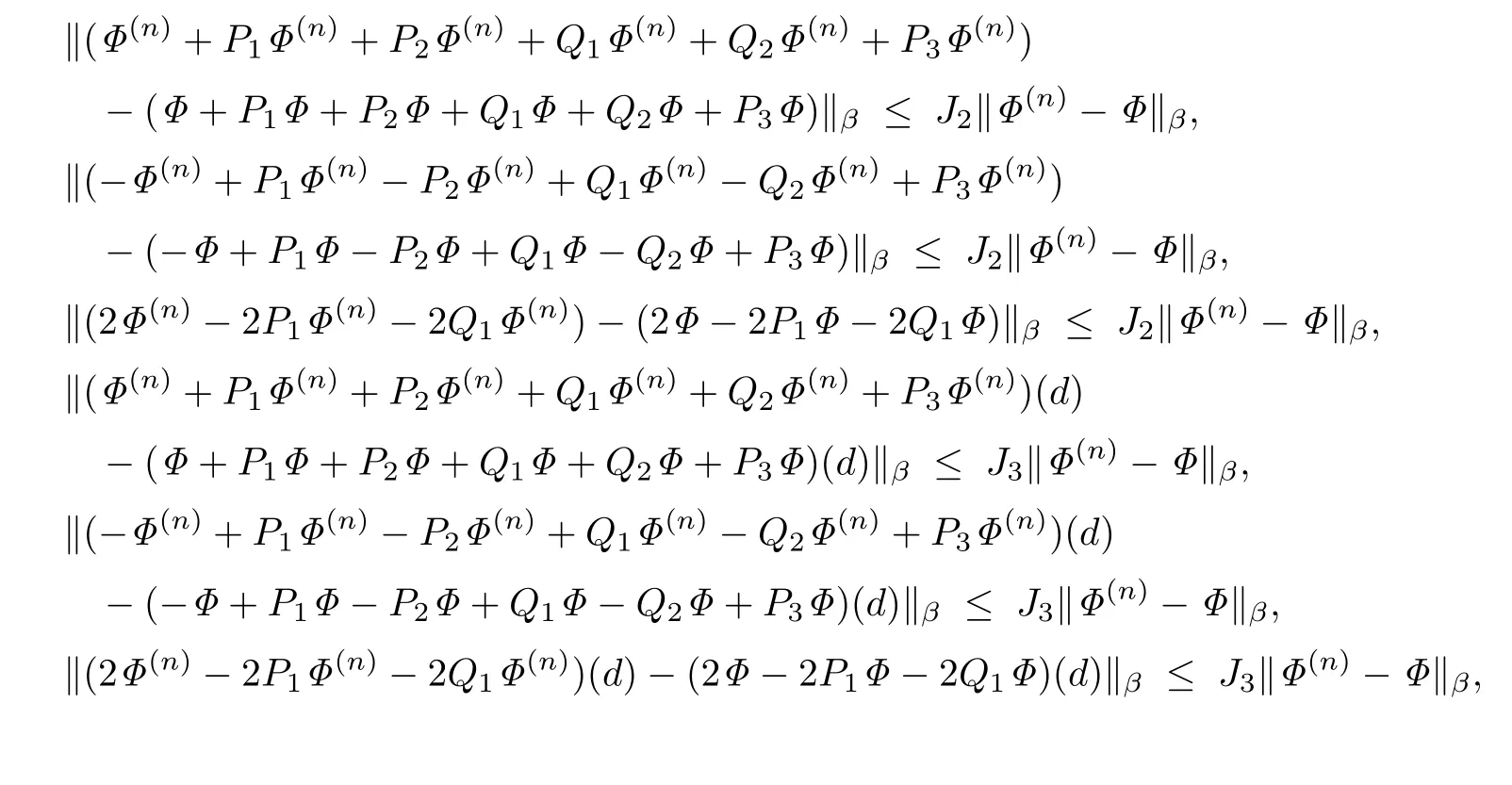
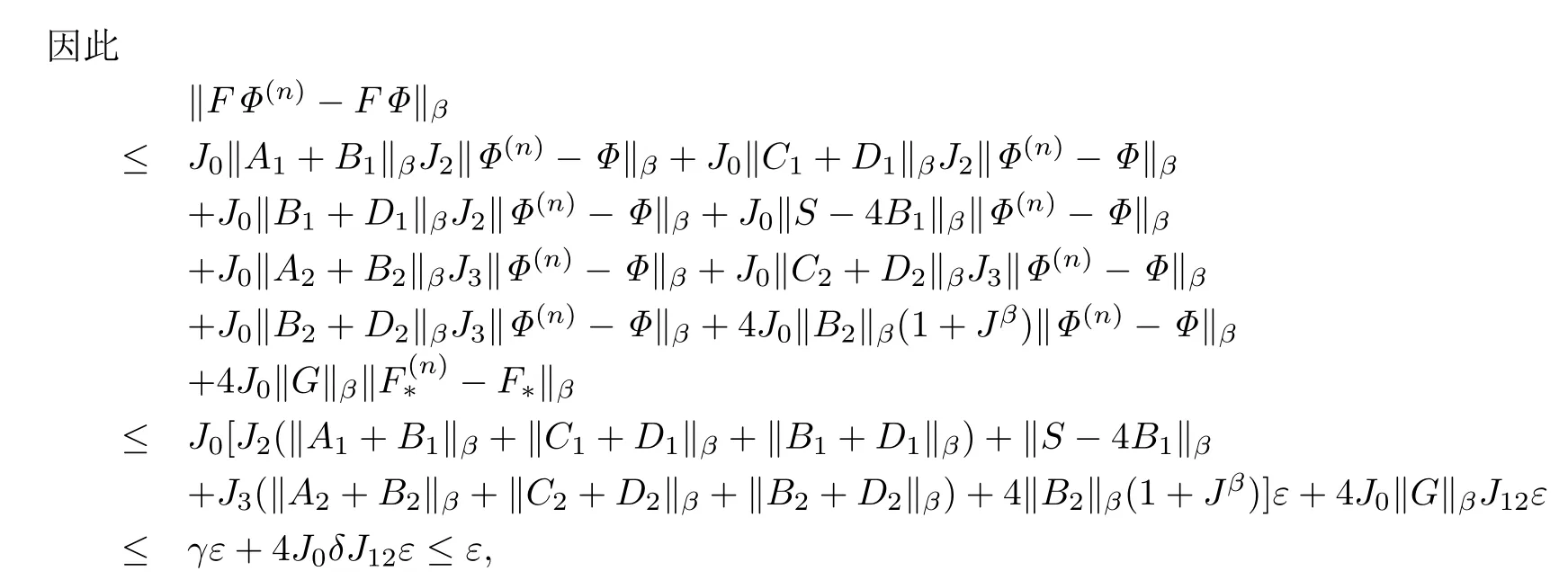
所以F是一个自身到自身的连续映射.

根据Arzela-Ascoli定理,F(T)是连续空间C(∂Ω1×∂Ω1)上的紧子集.由Schauder不动点定理知,至少存在一个函数向量Φ0∈Hp(∂Ω1×∂Ω2,β,Clm+k+2,0(R))满足FΦ0=Φ0,且解的积分表达式由(2.3)式给出.

证令T1={Φ|Φ=(φ1,φ2,……,φp)∈Hp(∂Ω1×∂Ω2,β,Clm+k+2,0(R)),‖Φ‖β ≤1}.

先证F是自身到自身的映射,即证对于任意的Φ ∈T1,有FΦ ∈T1.

任意的Φ ∈T1,由函数向量的性质,推论2.6,推论2.7和(3.5)式得

显然对于任意的Φ ∈T1,Φ ∈Hp(∂Ω1×∂Ω2,β,Clm+k+2,0(R)),有

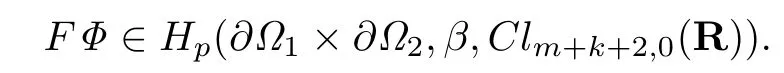
所以FΦ ∈T1.因此F是自身到自身的映射.

对于任意的Φ1,Φ2∈T1,有

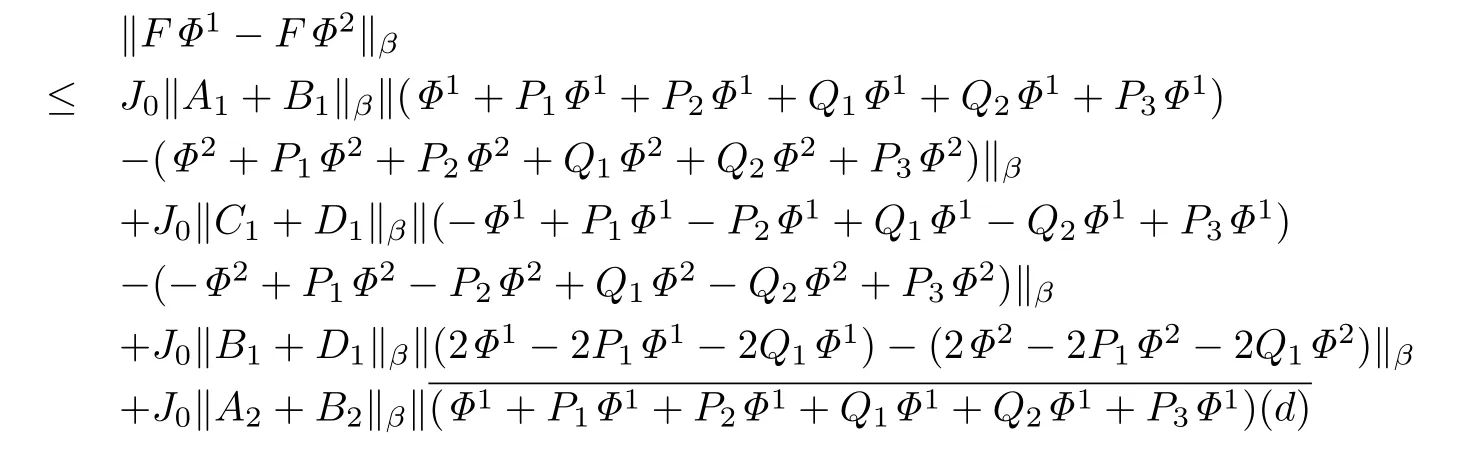
因为0＜γ ＜1,所以F是压缩映射.

由压缩映射原理可以知道,L问题存在唯一解,且解的表达式由(2.3)式给出.