一类新的求解双边障碍问题的数值方法
2021-07-02冉清华程晓良
冉清华 程晓良
(1.浙江大学 数学科学学院,浙江杭州 310000;2.贵州大学 数学与统计学院,贵州贵阳 550000)
§1 引言
障碍问题是典型的第一类变分不等式,它出现在物理,工程,金融和管理科学等领域并有着广泛的应用,比如润滑理论中的弹塑性扭转问题,弹性理论中的薄膜问题,尾流问题以及期权定价等.
假设Ω是R2上的一个具有Lipschitz边界∂Ω的有界域.给定函数f ∈L2(Ω),φ,ψ ∈H1(Ω)满足φ ≤ψ,φ|∂Ω ≤0及ψ|∂Ω ≥0.令在Ω中几乎处处成立},双边障碍问题描述为:求u ∈K,使得

对该问题的物理解释为:位于区域Ω且边界固定在∂Ω的弹性膜,在垂直力τf(τ为弹性膜的张量系数)的作用下的平衡位置u(膜的垂直位移分量)满足式(1),其中φ,ψ分别为下障碍和上障碍的高度.问题(1)存在唯一解.根据能量最小原理,解u可以用变分不等式形式来刻画[2]:

进一步,假设f ∈C(Ω),ψ ∈C(Ω),φ ∈C(Ω)和u ∈C2(Ω)∩C(),障碍问题又可表述为自由边界的偏微分方程的形式:

其中,Ω0={x ∈Ω|φ <u <ψ}表示膜与障碍不接触的区域,Ω1={x ∈Ω|u=φ}和Ω2={x ∈Ω|u=ψ}分别表示膜与下障碍,上障碍接触的部分,满足Ω=Ω0∪Ω1∪Ω2.由于Ωi(i=0,1,2)是未知的,(3)属于非线性问题.
作为一类经典的问题,障碍问题受到了许多研究者的关注,下面简单回顾一些已有算法.投影松弛法[3-4]是最著名的方法.它们具有收敛,易于实现的特点.然而,其收敛速度依赖于松弛参数的选择和与网格尺寸相关的自由度的数目[5].有效集策略[5-6]是一种求解离散障碍问题的有效方法,其基本迭代包括两个步骤.首先,根据某个指定准则将离散区域分解为活动部分和非活动部分.然后,在非活动集部分求解简化的线性系统.多重网格算法[7-9]可以使用迭代算法构造合理的域划分,其收敛速度不依赖于网格尺寸,但需要在某些子域上采用非线性求解算法.“活动障碍”法[10],分片线性迭代算法[11-12],罚方法[13],区域分解法[14]等也相继被提出,具有较好的效果.基于离散障碍问题的互补形式,本文通过引入一个参变量将原不易求解的互补问题等价改写为易于数值实现的等式方程组,并利用牛顿迭代法进行数值求解.
论文余下部分的结构如下:§2给出了双边障碍问题的等价描述.§3将所得的等价系统正则化并给出了迭代算法.§4数值实验说明了本文算法的有效性.最后,§5对全文进行了总结.
§2 双边障碍问题的等价描述
本文考虑障碍问题的数值求解,故首先将问题(1)离散,得到有限维障碍问题:

其中

和fff=(f1,f2,……,fm)T分别对应φ(x),ψ(x) 和f(x)的离散形式,(·,·)表示欧式空间Rm中的内积.刚度矩阵A=(aij)∈Rm×m是对称正定的.记I={1,2,……,m}为所有离散节点构成的集合.类似于连续情况,问题(4)具有唯一解,并且可以得到如下等价的离散障碍问题[3-6,12].
引理2.1下面三个条件等价.

显然,离散障碍问题的上述三种等价形式分别对应于能量极小化问题(1),变分不等式(2),自由边界的偏微分方程(3)的离散.关于上述离散结果的收敛性可类似于[3]中单边障碍问题的讨论进行分析,这里不给出细节.本文着重介绍离散系统(6)的求解.对于离散障碍问题(6)的数值求解,已有很多算法被提出.例如,活动集策略是求解离散障碍问题的有效方法,但是为了使迭代过程有效,需要应用适用于非正则几何区域的快速线性系统求解器,在大规模计算中收敛较慢.[12]首先将离散障碍问题转化为分片线性系统
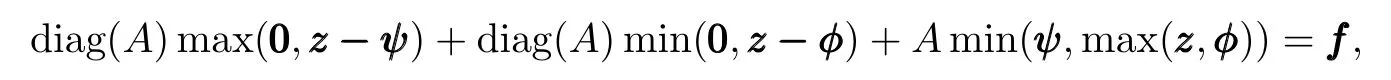
然后应用皮卡迭代算法求解得到uuu=min(ψ,max(zzz,φ)).虽然该算法能在有限步收敛到离散障碍问题的解,但是其收敛速度较慢,而且计算过程复杂.基于此,本文提出如下计算方法.
首先介绍两个辅助函数.对于i=1,2,……,m,定义函数gi:θ ∈R→gi(θ)∈R:
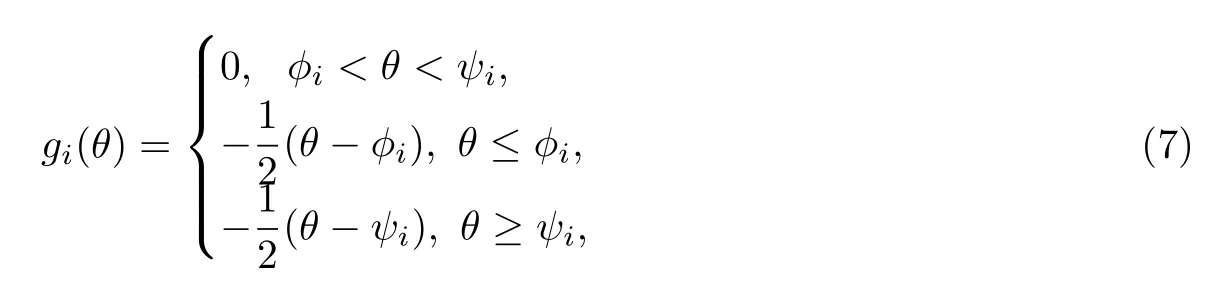
和pi:θ ∈R→pi(θ)∈R:

为了更直观的表达,图1给出了gi(θ)和pi(θ)的图像.

图1 gi(θ)和pi(θ)的图像
现在给出本文的主要结果.引入变量Θ=(θ1,θ2,……,θm)T∈Rm,构造如下等式方程组:
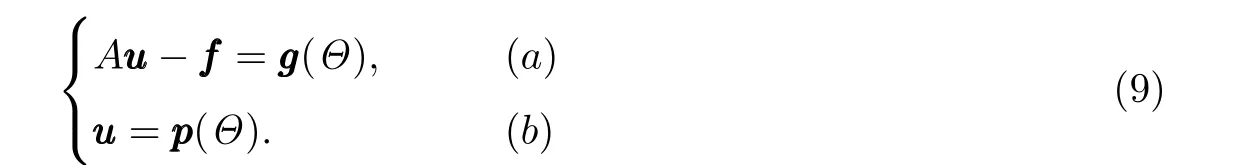
其中,ggg:Θ ∈Rm →ggg(Θ)=(g1(θ1),g2(θ2),……,gm(θm))T∈Rm,ppp:Θ ∈Rm →ppp(Θ)=(p1(θ1),p2(θ2),……,pm(θm))T∈Rm.下面证明所构造的系统(9)与离散障碍问题(6)是等价的.
定理2.2存在Θ=(θ1,θ2,……,θm)T∈Rm使得系统(9)与问题(6)等价.
证 (⇒) 假设uuu是(9)的解.根据(9)(b)和ppp(Θ)的定义可得φi ≤ui ≤ψi,i=1,2,……,m.下面进行分类讨论.
若φi <ui <ψi即,则由(9)(b)可得φi <pi(θi)<ψi.根据pi(·)的定义可知φi <θi <ψi.从而gi(θi)=0.因此,(Auuu)i-fi=0.
若ui=φi即,通过(9)(b)和(8)可以得到θi ≤φi.因此

若ui=ψi即,则由(9)(b)可得pi(θi)=ψi.故θi ≥ψi.从而

综上可得,uuu为问题(6)的解.
(⇐) 假设uuu是(6)的解,下证存在Θ=(θ1,θ2,……,θm)T∈Rm使得uuu满足系统(9).
若,则(Auuu)i-fi=0且φi <ui <ψi.取θi=ui,则成立

若,则(Auuu)i-fi ≥0且ui=φi.根据gi(·),pi(·)的定义,显然存在θi ≤φi使得

而且,由gi(·)的单调性可知θi是唯一存在的.
若,(Auuu)i-fi ≤0且ui=ψi.类似地,存在唯一的θi ≥ψi使得

综上所述,存在Θ=(θ1,θ2,……,θm)T∈Rm使得(uuu,Θ)满足(9).
显然从定理的证明过程可以得到如下结论.
定理2.3系统(9)存在唯一解(uuu,Θ).
本节通过引入一个参数Θ,将原非线性的不等式问题(6)等价转化为等式方程组(9),使得问题更容易计算.由于(9)是一个非线性系统,可以考虑用牛顿迭代法进行求解.
§3 正则化及迭代算法
众所周知,牛顿迭代法的最大优点是收敛速度快,其在单根附近具有二阶收敛速度.牛顿迭代法也因此而被广泛使用.下面,本文利用该方法计算系统(9).
由于系统(9)中的gi(θ)和pi(θ)不可导,首先对其进行正则化处理.分别定义gi(θ)及pi(θ)的C1近似gic(θ),pic(θ):

其中常数c >0.gic(θ),pic(θ) 的函数图像如图2所示.不难证明,当c →∞时,

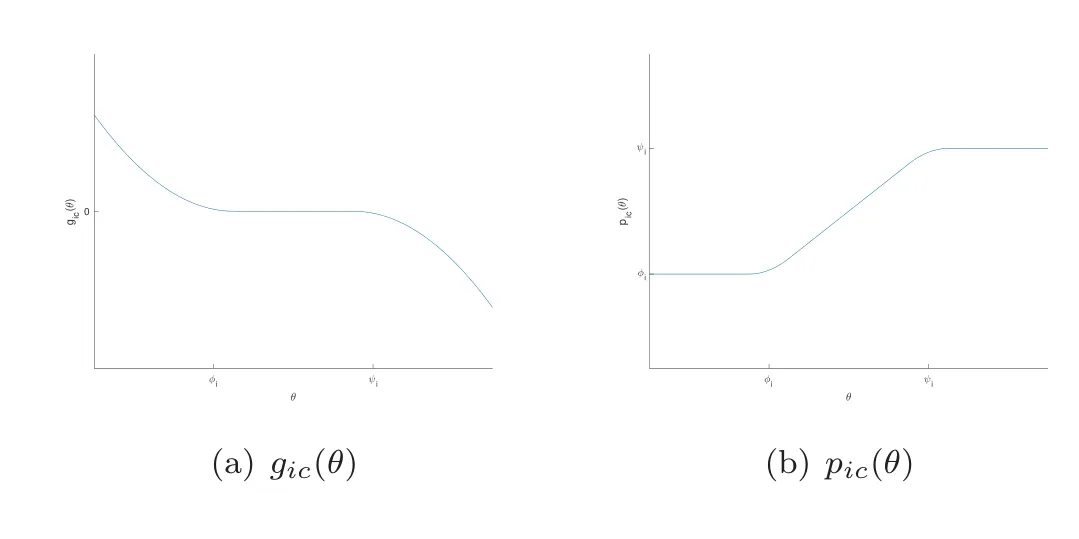
图2 gic(θ)和pic(θ)的图像
因此得到系统(9)的正则化结果:
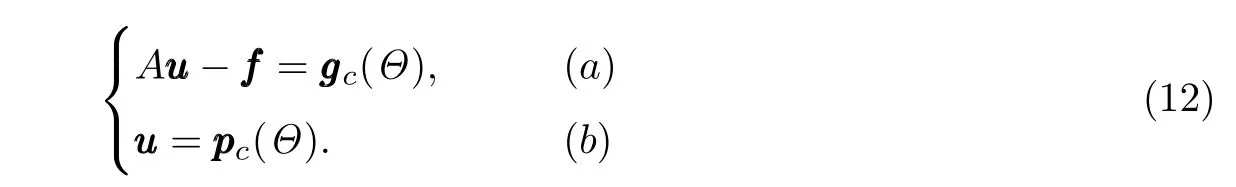
其中gggc(Θ)=(g1c(θ1),g2c(θ2),……,gmc(θm))T,pppc(Θ)=(p1c(θ1),p2c(θ2),……,pmc(θm))T.利用牛顿迭代法的思想,得到关于(uuu,Θ)的如下线性系统:
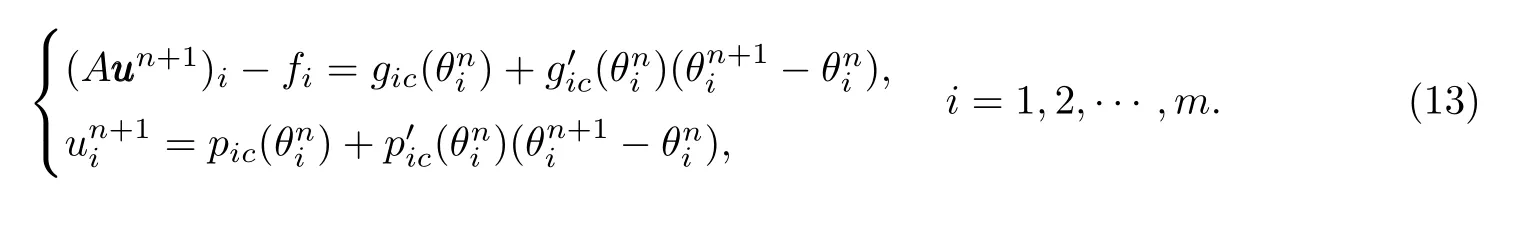
其中

从而将原问题转化为如下代数系统:
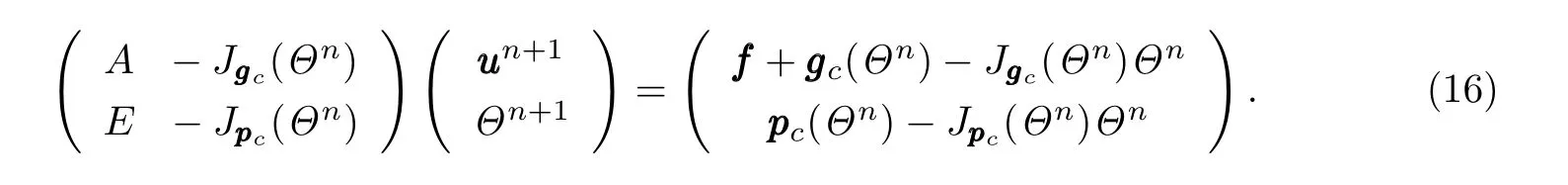
其中,E是Rm×m中的单位矩阵,
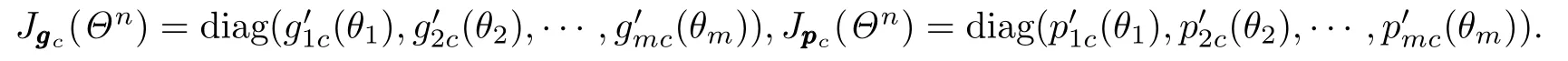
基于上述分析,给出求解障碍问题的如下算法步骤.
算法
第1步 输入参数:正则化参数c,网格尺寸h,误差精度∈0,初始值uuu0,Θ0,n ←0.
第2步 根据(16)求解uuun+1,Θn+1.
第3步 如果‖Θn+1-Θn‖<∈0,停止迭代并输出uuun+1;否则n ←n+1,转第2步.
注通过系统(13)不难发现,当Θn+1=Θn时,(uuun+1,Θn+1)是问题(12)的精确解.故算法中将‖Θn+1-Θn‖设置为停止准则是合理的.
§4 数值模拟
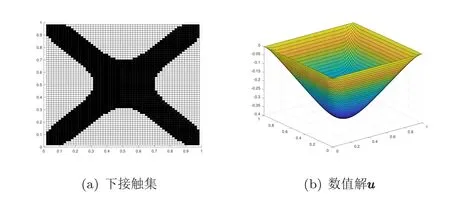
图3 例1的数值结果

图4 例2的数值结果

图5 例3的数值结果
在本节中,通过以下四个例子来说明本文所提出的算法的有效性.所有实验均在系统配置为8G内存,2.3GHz Intel Core i5处理器,Matlab版本为R2018b的个人计算机上进行.以下各例中,Ω=[0,1]×[0,1],并采用绝对误差en+1=‖Θn+1-Θn ‖2<∈0=10-6作为迭代停止准则,其中‖ · ‖2为欧式范数.除非特别说明,所得实验结果均在c=108,h=1/64,Θ0=uuu0=Afff的情况下获得.
例1f(x,y)=-8,φ(x,y)=-dist((x,y),∂Ω),ψ(x,y)=dist((x,y),∂Ω).[13]
例2f(x,y)=11(x+y-1),φ(x,y)=-dist((x,y),∂Ω),ψ(x,y)=dist((x,y),∂Ω).[13]
例3[5,15]φ(x,y)=-dist((x,y),∂Ω),ψ(x,y)=0.2,
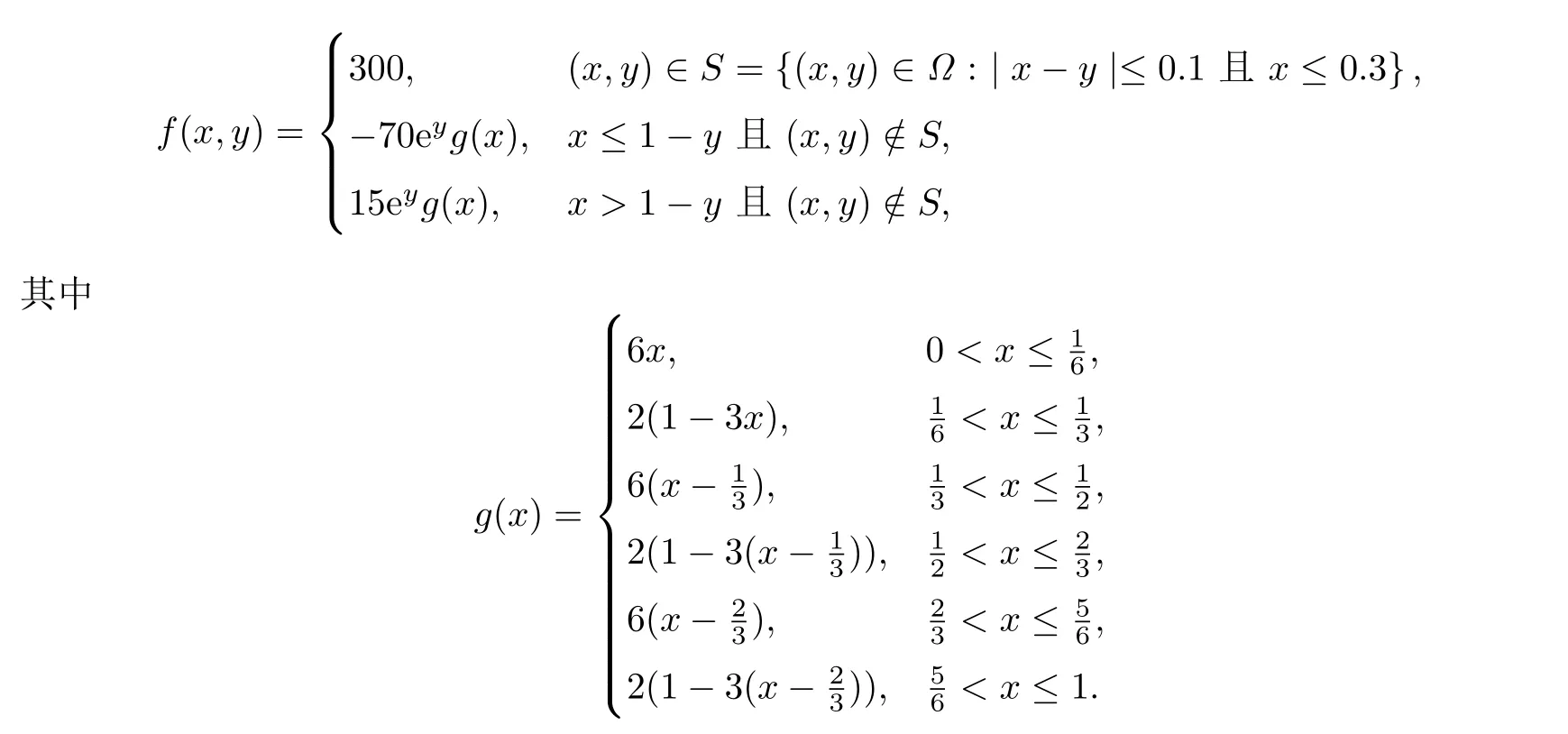
例4f(x,y)=45(x-x2)(sin(11πx)+1),ψ(x,y)=dist((x,y),∂Ω),φ(x,y)=-∞.[5]
以上各例的数值结果如图3-图6所示.图中上接触集和下接触集的白色区域分别表示数值解与上障碍和下障碍接触的区域.例1的数值解与上障碍没有接触.例4的数值解与下障碍没有接触.各例的迭代次数n及误差en随网格尺寸h变化的情况如表1所示.图3-6以及表1的数据说明,本文算法能有效,快速地计算出数值解,而且收敛速度不依赖于网格尺寸.

图6 例4的数值结果
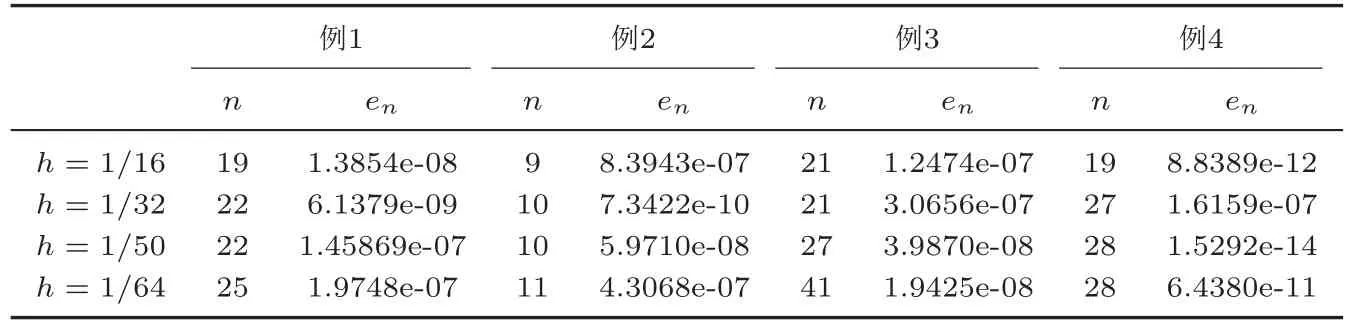
表1 迭代次数及误差随网格尺寸变化的情况
§5 结语
本文通过引入一个参数,将离散双边障碍问题的互补形式等价地改写为易于求解的方程组,并将其正则化处理之后,运用牛顿迭代法进行数值求解.数值结果显示该方法能快速,准确地计算出数值解及接触集,其收敛速度不依赖于网格尺寸的选取.
