基于中径和预紧摩擦力匹配的导轨副装配研究*

2021-07-02俞福春冯虎田

组合机床与自动化加工技术 2021年6期

俞福春，欧屹，王凯，冯虎田

(南京理工大学机械工程学院，南京 210094)

0 引言

滚珠直线导轨副具有运动精度高、磨损小、润滑简便等优点，是数控机床的核心功能部件，其性能的优劣对数控机床整体性能以及精度有着重要的影响[1]。滚珠直线导轨副滚道中径的偏差量是高精度机床的重要性能指标，其精度直接影响滚珠直线导轨副的预紧摩擦力与装配尺寸。

针对滚珠直线导轨副型面参数偏差对导轨副预紧摩擦力影响的研究，孙健利等[2-3]分析差动润滑和弹性滞后对滚珠直线导轨副摩擦力的影响，得到滚珠过盈量与摩擦力之间的关系，未涉及关于导轨副中径的影响。张巍等[4]通过分析每个滚珠的受力、变形与预紧力，建立了刚度、预紧力、接触角、摩擦力和临界载荷与滚珠直线导轨磨损之间的关系模型，其侧重于滚珠变形对导轨副刚性影响，未涉及导轨副中径偏差带来的预紧摩擦力变化。陆艮峰[5]基于Hertz接触理论，建立导轨副静刚度理论模型，重点分析外载荷、预紧力和滚道曲率比对导轨副刚度的影响，侧重于力学模型的建立。以上研究主要分析滚珠直径偏差以及几何误差对滚珠直线导轨副摩擦力的影响，但尚未涉及滑块、导轨滚道中径偏差对导轨副摩擦力的影响。

针对滚珠直线导轨副滑块中径测量的研究，目前工厂主要采用手持式测量，这种方式受人为因素影响大。李桂明[6]提出了一种接触式测量滚珠直线导轨副滑块中径的量具，并且给出了滑块中径测量方法以及误差分析。针对滚珠直线导轨副高效装配的研究，韩军君等[7]根据理论计算与基准导轨装配滑块组件的方式，确定具体的导轨副中径加工精度，但没有给出预紧摩擦力计算方式。吕祎[8]从导轨副关键精度着手，确定关键工序加工方法、精度保证手段和检测方法，使得优化后预紧力满足要求。以上研究缺乏针对已加工的导轨副，在满足预紧摩擦力条件下实现高效装配。

本文在前人研究的基础上，提出了根据中径偏差计算预紧摩擦力的方法，并设计非接触式导轨副滚道测量装置。以预紧摩擦力精确控制为主要目标，通过测量导轨副滚道中径参数，经过对预紧摩擦力的计算完成组件的匹配，实现滚珠直线导轨副的高效装配。

1 滚道中径及滚珠直径偏差对间距影响

1.1 滚珠直线导轨副滚珠滚道接触模型

常用滚珠直线导轨副(以下称为导轨副)几何特征及滚道分布如图1所示。滚珠直线导轨副主要由滑块、导轨以及滚珠三个部分组成，本文研究的滚珠直线导轨副为四列对称结构的滚珠型直线导轨副。

图1 滚珠直线导轨副结构及滚道分布

滚珠直线导轨副滚道中径如图2a所示，四列滚珠分别编号为i=1,2,3,4，设滑块与导轨之间的四列滚珠的初始接触角均为α，以导轨副的对称中心为原点建立空间直角坐标系o0-x0y0z0，x0轴方向为滑块沿导轨滑动方向，y0轴方向为水平线上沿导轨径向方向，z0轴与x0轴、y0轴满足右手系准则。其中，Ls表示滑块左列滚道(i=2,3)与右列滚道(i=1,4)曲率中心的距离，记为滑块滚道中径；Lg表示导轨左列滚道(i=2,3)与右列滚道(i=1,4)曲率中心的距离，记为导轨滚道中径。本文涉及导轨副滚道中径包括滑块滚道中径以及导轨滚道中径。滚珠直线导轨副滚道间距如图2b所示，滑块滚道曲率中心与导轨滚道曲率中心连线上，分别与滑块滚道、导轨滚道相交于M、N点，线段MN即为导轨副的滚道间距。

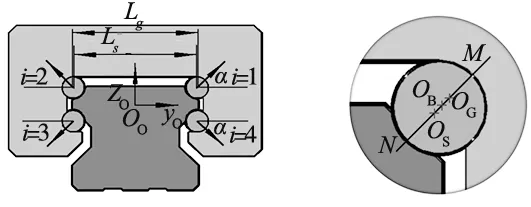
(a)导轨副滚道(b)滚道间距图2 导轨副滚道中径及滚道间距

导轨副中径的偏差直接影响导轨副滚道间距变化，这里将导轨副滚道中径偏差分为4种情况，如图3所示。与标准导轨副相对比，导轨滚道中径偏大称为导轨外扩，如图3a所示；导轨滚道中径偏小称为导轨内缩，如图3b所示；滑块滚道中径偏小称为滑块外扩，如图3c所示；滑块滚道中径偏大称为滑块内缩，如图3d所示。

标准中径导轨副中径偏差导轨副图3 导轨副滚道中径偏差

(1)

滚珠直线导轨副的预紧力是通过增大滚珠直径，与滑块滚道、导轨滚道之间的过盈配合来实现。以此来提高滚珠直线导轨副的刚性，消除滚珠与滚道之间的间隙。由于滑块与导轨的刚度相对于滚珠刚度强，产生预紧力的形变主要是源于滚珠的形变，本文在假设滑块与导轨为刚体的基础上进行研究。

下面以某公司生产的HGH35HA型滚珠直线导轨副为研究对象，该型号导轨副参数如表1所示。

表1 HGH35HA型滚珠直线导轨副参数

滚珠在预紧力的作用下滚珠的弹性接触变形量记为2δ0，滚珠直径为R，对应的预紧力为Q0。式(2)中，i表示导轨副的滚道数,i=4；z表示单列承载区滚道数量；Q0表示单个滚珠所受预压力。

(2)

结合Hertz理论[9]，可计算得滚珠在预紧力的作用下滚珠接触变形量2δ0=0.027 mm。

(3)

式中，δ0为滚珠的形变量；K,μ为与接触椭圆的椭圆率相关系数；v,E为导轨副材料的泊松比与弹性模量；∑ρ为滚珠直径及滚道曲率相关系数。

1.2 导轨副滚道中径偏差与接触角的关系

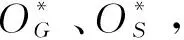
标准导轨副偏差后导轨副图4 导轨副滚道中径与接触角关系

2RB(fS+fG-1)-2δ0

(4)

(5)

针对导轨外扩模型与滑块外扩模型，如图4a、图4b所示几何关系可知：

(6)

如令fG=fS=f,则导轨外扩模型与滑块外扩模型滚道中径偏差之后的导轨副接触角α*为:

(7)

针对导轨内缩模型与滑块内缩模型，如图4c、图4d所示几何关系可知：

(8)

如令fG=fS=f,则导轨内缩模型与滑块内缩模型滚道中径偏差之后的导轨副接触角α*为：

(9)

相对于标准滚动直线导轨副滚道中径尺寸，导轨外扩模型与滑块外扩模型的滚道中径偏差量记为正值，导轨内缩模型与滑块内缩模型的滚道中径偏差量为负值。在导轨副初始接触角为45°情况下，导轨副中径偏差量ΔL对接触角的影响如图5所示。

图5 导轨副滚道中径偏差与接触角关系

如图5所示，对于导轨外扩模型与滑块外扩模型，随着滚道中径偏差量的增加，导轨副接触角减小；对于导轨内缩模型与滑块内缩模型，随着滚道中径偏差量的增加，导轨副接触角增大。

1.3 导轨副滚道中径偏差与滚道间距模型

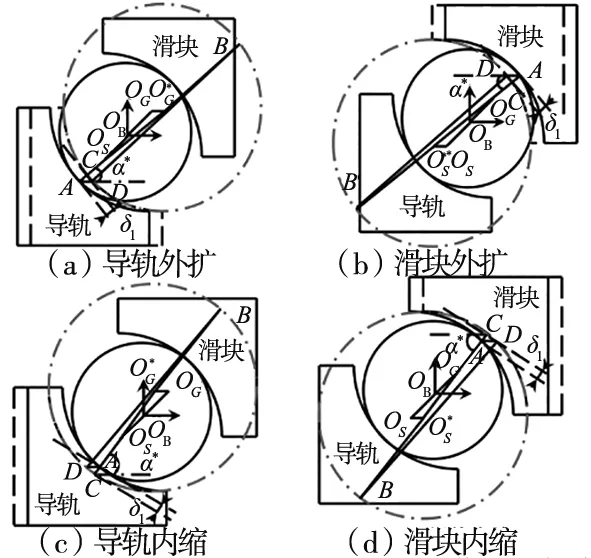
标准导轨副滚道轮轮框圆偏差后导轨副图6 导轨副滚道中径偏差与滚道间距关系

(10)

(11)

(12)

即：

(13)

滚道间距在导轨副初始接触角为45°情况下，导轨副中径偏差量ΔL对滚道间距的影响如图7所示。记在相对于标准滚动直线导轨副滚道中径尺寸情况下，横轴方向：导轨外扩模型与滑块外扩模型的滚道中径偏差量为正值，导轨内缩模型与滑块内缩模型的滚道中径偏差量为负值。纵轴方向：滚道间距增大为正值，滚道间距减小为负值，滚道中径偏差对滚道间距的影响几乎成线性关系。

图7 不同滚道中径下滚道间距

1.4 导轨副滚道中径偏差与滚珠直径偏差等效关系

滚珠直线导轨副的滑块滚道以及导轨滚道均为圆柱面，对于滚珠和两个圆柱面之间的刚性接触，运动学约束[10]要求接触点位于一条平行于圆柱表面曲率点连线的直线上。如图8a所示，当滚珠与圆柱面之间没有弹性形变时，接触点连接线与曲率中心连接线平行；如图8b所示，当滚珠与圆柱面之间由于挤压发生弹性形变时，接触点与曲率中心共线，即接触点位于滚道间距上。

(a)无挤压状态(b)挤压状态图8 刚性滚动接触

本文滚珠与滚道之间存在弹性形变，刚性滚动接触情况如图8b所示,滚珠与两圆柱面接触点位于两圆柱面的曲率中心连线上。此时滚珠直径偏差量2δ2等于滚珠沿滚道间距方向形变量2δb，即:

δ2=δb

(14)

针对实际加工中出现的由于滚珠直线导轨副滚道中径偏差而产生的预紧摩擦力变化的问题，根据导轨副中径偏差与滚道间距的关系模型以及滚珠直径偏差与滚道间距的关系，建立导轨副滚道中径偏差与滚珠直径偏差等效关系。应用于装配过程中，在已测得导轨副滚道中径的情况下，通过改变滚珠直径大小，来解决由于滚珠直线导轨副滚道中径偏差而产生的预紧摩擦力变化的问题，实现高效装配。

根据式(13)、式(14)，令滚道间距变化量相等，得到导轨副滚道中径偏差与滚珠直径偏差等效关系式，即：

(15)

(16)

(17)

2 滚道中径及滚珠直径偏差对预紧摩擦力影响

本文研究滚珠直线导轨副滚道中径对滑块滚道、导轨滚道与滚珠之间预紧摩擦力的影响，该摩擦力受滚珠与滑块滚道、导轨滚道之间摩擦系数以及滚珠沿滚道间距方向上形变量的影响。其中摩擦系数固定，滚珠沿滚道间距方向上的形变量分为两种情况：滚珠自身直径偏差引起的滚珠沿滚道间距方向上的形变量；滑块滚道中径偏差、导轨滚道中径偏差引起的滚珠沿滚道间距方向上的形变量。

2.1 导轨副预紧摩擦力的计算

滚珠直线导轨副在运动过程中，导轨副预紧摩擦力由滑块内滚珠的内循环系统以及刮油片的阻力产生。内循环系统由滑块中的滚珠经由反向器连接承载区与非承载区构成。滚珠于承载区与非承载区的摩擦特性不相同，承载区的摩擦力与法向载荷Q相关，非承载区的摩擦力远小于承载区摩擦力，可以忽略不计。滚珠在承载区的摩擦状态，可视为滚珠在平面上的摩擦运动，服从库仑定律。则导轨副预紧摩擦力关系式为：

Ff=4·μ0·z·Q+S

(18)

其中，μ0表示滚珠在承载区的摩擦系数，常数4表示滑块沟槽数，z表示导轨副中每列承载滚珠数，Q表示单个滚珠所受法向载荷，S表示刮油片阻力，HGH35HA型滚珠直线导轨副刮油片阻力为3.04 N。本文所研究的滚珠所受法向载荷来自于滚珠的弹性型变而产生的载荷。结合Hertz理论公式(3)可得：

(19)

当滚珠沿滚道间距方向变形量已知，结合式(18)、式(19)求得导轨副运动过程中的摩擦力，即：

(20)

2.2 滚珠直径偏差对导轨副预紧摩擦力的影响

滚珠直径的偏差影响滚珠沿滚道间距方向的形变量，进而影响滚珠所受法向载荷，最终改变摩擦力大小。根据式(19)可得滚珠直径偏差下的滚珠法向载荷Qb：

(21)

联系滚珠预加载荷式(3)以及摩擦力式(18)，可得滚珠直径偏差与导轨副预紧摩擦力的关系：

Ffb=4·μ0·z·Qb+S

(22)

2.3 滚道中径对导轨副预紧摩擦力的影响

导轨副滚道中径偏差影响滚珠沿滚道间距方向的形变量，进而影响滚珠所受法向载荷，最终改变摩擦力大小。根据式(19)可得导轨副滚道中径偏差下的滚珠法向载荷QL：

(23)

联系滚珠预加载荷式(3)及摩擦力式(18)可得，导轨副中径偏差与导轨副预紧摩擦力的关系：

FfL=4·μ0·z·QL+S

(24)

图9 不同滚道中径下的预紧摩擦力

如图9所示，为滚道中径偏差与导轨副预紧摩擦力之间的对应关系。其中，K(0，11.552)表示中径偏差量为0 mm时，对应的导轨副预紧摩擦力，即标准导轨副在有初始预加载荷情况下的导轨副预紧摩擦力。由图9可知，在预紧摩擦力范围内，导轨副预紧摩擦力与中径偏差量成非线性关系。对于导轨外扩模型与滑块外扩模型，随着中径偏差量的增加，导轨副预紧摩擦力变化速率增加；对于导轨内缩模型与滑块内缩模型，随着中径偏差量的增加，导轨副预紧摩擦力变化速率减小。

3 试验验证

为了验证导轨副中径偏差对预紧摩擦力的影响，依次改变滑块滚道中径、导轨滚道中径或者滚珠直径大小，通过更换不同尺寸的部件重新装配后测量导轨副预紧摩擦力。并根据导轨副的装配实验，可以验证高效装配方案的可行性。

3.1 试验设备及方法

针对导轨副型面参数对于摩擦力影响的研究，采用控制变量法，设计如下三组试验：

(1) 导轨滚道中径、滚珠直径不变，分别测量5个不同滑块滚道中径值下的导轨副预紧摩擦库伦力；

(2) 滑块滚道中径、滚珠直径不变，分别测量5个不同导轨滚道中径值下的导轨副预紧摩擦力；

(3) 滑块滚道中径、导轨滚道中径不变，分别测量5个不同滚珠直径下的导轨副预紧摩擦力。

针对导轨副滚道型面特点，设计了非接触式导轨副型面检测试验台对滑块滚道中径、导轨滚道中径进行测量，如图10所示，试验台包括驱动装置、测量装置、控制台、导轨副托架等部分。测量方案如图11所示，分别采用两对传感器1、2和3、4平行滚道轴线X方向移动扫描，获取滑块底面与侧面基准面内两条直线数据，来反映两基准面平面度；由于滑块滚道中心距限制，传感器无法直射滚道面，将传感器5、6斜置于滑块、导轨外侧，平行Z轴方向移动来获取滑块、导轨滚道截面。

图10 非接触式导轨副中径检测试验台

(a)滑块测量 (b)导轨测量

利用滚动直线导轨副预紧摩擦力测量试验台对导轨副预紧摩擦力进行测量，如图12所示，试验台包括控制柜、测量装置、驱动装置以及花岗岩床身。测量装置当中，通过力传感器推动被测滑块沿导轨匀速运动时，力传感器测量的数值即为导轨副中的摩擦力。

(a)测量试验台 (b)测量装置

3.2 预紧摩擦力测量结果分析

以1 m/min采集导轨副的正向摩擦力，每组摩擦力测量三次取其平均值。本文为获取不同滑块、导轨滚道中径值，分别测量不同厂家的相同理论尺寸的导轨副。其中以某厂家的HGH35HA型滚珠直线导轨副的滑块滚道中径值、导轨滚道中径值、滚珠直径值作为标准型面参数值，记为标准导轨副，如表2、表3、表4中第一行所测值，分别为33.780 mm、33.820 mm、6.347 mm。

表2 滑块滚道中径偏差下导轨副预紧摩擦力

表3 导轨滚道中径偏差下导轨副预紧摩擦力

图13 滚道中径偏差下理论与实测预紧摩擦力对比

根据试验(1),导轨滚道中径、滚珠直径不变，分别测量5个不同滑块滚道中径值下的导轨副预紧摩擦力，测量结果如表2所示；根据试验(2) ,滑块滚道中径、滚珠直径不变，分别测量5个不同导轨滚道中径值下的导轨副预紧摩擦力，测量结果如表3所示。表2、表3中，对中径测量的数据取平均值后，计算每一组相对第一组平均值的中径偏差值；利用中径偏差值计算对应的理论预紧摩擦力，进而求解相对试验预紧摩擦力的偏差值。在标准导轨副的基础上，分别替换表2所测得不同滑块滚道中径的滑块、表3所测得不同导轨滚道中径的导轨，重新装配测量导轨副的预紧摩擦力，得到如图13所示的导轨副的理论、试验预紧摩擦力随滚道中径变化关系。

综上所述，试验(1)、试验(2)测量值与理论计算所得导轨副预紧摩擦力变化趋势相同；测量结果与理论计算预紧摩擦力最大偏差为6.89%，总体精度满足要求。实验测得的导轨副预紧摩擦力小于理论计算所得导轨副预紧摩擦力，主要原因可能是数值计算中滑块视为刚体，忽略了滑块自身的形变影响。试验验证了滚道中径对导轨副预紧力影响关系的准确性。

根据试验(3)，滑块滚道中径、导轨滚道中径不变，分别测量5个不同滚珠直径下的导轨副预紧摩擦力，测量结果如表4所示。

表4 滚珠直径偏差下导轨副预紧摩擦力

对滚珠直径测量数据取平均值，计算每一组相对第一组平均值的直径偏差值；利用直径偏差值求解出理论预紧摩擦力，与试验测得预紧摩擦力相比较得出预紧摩擦力的偏差值。测量结果与理论计算预紧摩擦力最大偏差为5.65%，总体精度满足要求，验证了滚珠直径偏差对导轨副预紧力影响关系的准确性。

综合表2、表3所得中径偏差值，根据导轨副滚道中径偏差与滚珠直径偏差等效关系求得对应等效滚珠偏差，再由等效滚珠偏差计算对应理论预紧摩擦力，并计算与试验预紧摩擦力偏差值，得到表5。其中预紧摩擦力最大偏差值为6.79%，总体精度满足要求，验证了导轨副滚道中径偏差与滚珠直径偏差等效关系的正确性。

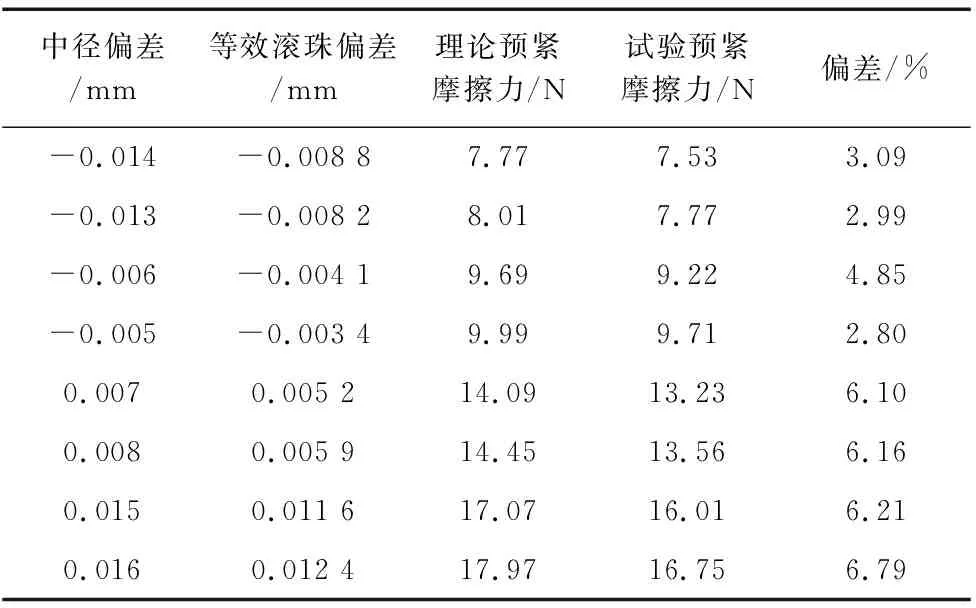
表5 滚道中径偏差与滚珠直径偏差等效预紧摩擦力

3.3 导轨副高效装配试验验证

按照如图14所示流程，在已知标准导轨副滚道中径基础上测量实际导轨副滚道中径，求解出滚道中径的偏差值。根据滚道中径偏差值，分别求得实际导轨副预紧摩擦力与等价滚珠直径偏差值。判断实际导轨副预紧摩擦力是否在目标预紧摩擦力范围内，如是，则原始滚珠即为适配滚珠；如否，则根据式(22)由实际与目标预紧摩擦力差值求得对应滚珠变形量，再加上等价的滚珠直径变形量，得到符合目标预紧摩擦力要求的滚珠。导轨副装配试验如图15所示。

图14 高效装配流程图

图15 导轨副装配

本文试验对象为HGH35HA型滚珠直线导轨副，预压等级为重预压，目标预紧摩擦力为14.7～17.1 N。根据该型号滚珠直线导轨副参数，通过适配滚珠以达到目标预紧摩擦力。

如表6所示，针对一对滑块和导轨的装配，当熟练的操作工可以一次性匹配合适尺寸公差的滚珠时，本文方案优势难以体现；当需要两次以上装配才达到目标预紧摩擦力时，本文装配方案的效率提升明显，对于三次人工装配的耗时，本文方案的装配效率提高已超过50%。考虑到目前的生产线大多为大批量零部件的统一装配，本文方案更加适合在构建零部件尺寸数据库后完成快速装配。