基于RBF神经网络的六自由度机械臂轨迹优化*

柘龙炫，李少波，张星星,宋启松

(贵州大学机械工程学院，贵阳 550025)

0 引言

六自由度机械臂具有较高的灵活性，能模仿人的手臂完成空间抓取动作，越来越广泛应用于国防、航天、医疗、日常生活等生产活动。机械臂作为机器人的主要执行机构，运用机械臂不但可以减少劳动力，降低劳动成本，还能提高产品的生产质量和效率，是未来工业发展的必然趋势[1]。当前机械臂在分拣、码垛以及装配等重复性流水作业中最为常见[2]。为了满足目前高效率生产的需求，国内外学者对机械臂轨迹规划已经进行了深入研究，如文献[1]选用D-H法建立机械臂在笛卡尔空间的运动学模型，对机械臂进行运动学分析，通过直线插补和圆弧插补对机械臂运动轨迹进行优化；文献[3]利用了自适应遗传算法在三次样条插值的基础上，对关节空间轨迹进行优化；文献[4]对比了三次多项式插值法与五次多项式插值法的关节轨迹规划效果，得出五次多项式插值后机械臂运动更为平稳；文献[5]建立了机械臂的D-H坐标系，将A*搜寻算法与拉格朗日插值法相结合，规划出机械臂的运动轨迹；文献[6]从运动学角度出发，提出基于RBF神经网络的圆弧轨迹规划，通仿真表明规划轨迹平滑、逼近误差小。与BP神经网络相比,RBF神经网络的规模大,且函数逼近能力、学习速度、分类和模式识别能力更优[7]。

基于上述内容，为了提高机械臂末端执行器的轨迹精度，设计了六自由度机械臂模型、并根据模型建立D-H坐标系与D-H参数表。通过机械臂的运动学求解得到末端执行器的运动位置和姿态，利用RBF神经网络对运动学得到的运动轨迹进行优化。

1 机械臂运动学分析

1.1 机械臂运动学模型

机械臂通常由若干关节和连杆按依次连接而成，如图1a所示，各个关节的运动可以是转动或滑动，各连杆长度根据实际需要，可以是任意值。机械臂运动学模型基于各关节和连杆建立的坐标系变换求得，因此根据机械臂模型，建立六自由度机械臂的D-H坐标系如图1b所示，其中o0-x0y0z0为固定参考坐标系，通常将其固定在基座上。

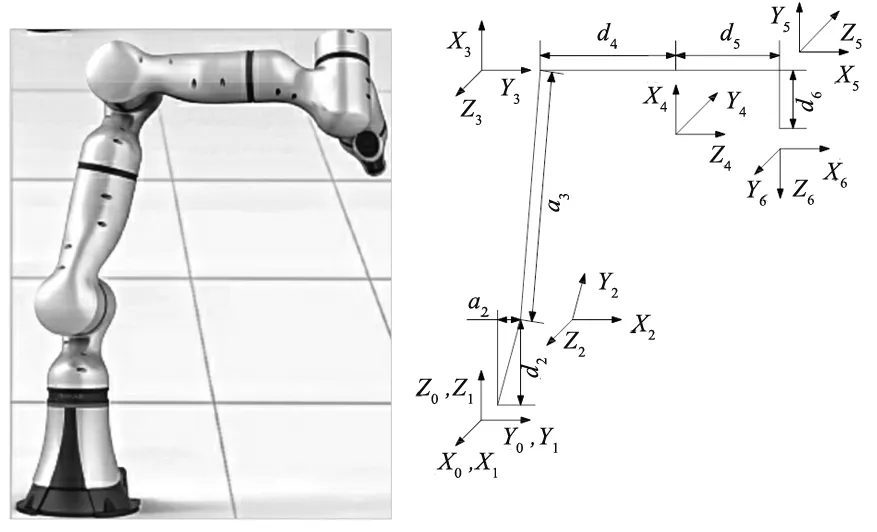
(a) 机械臂模型 (b) D-H坐标系图1 机器臂模型及其D-H坐标系

1.2 相邻连杆间参数确定

如图2所示，轴zn与关节n+1的轴线重合，根据关节n+1的旋转方向，按右手定则判定轴zn方向；轴xn与公法线an重合，方向沿an由轴线zn-1指向轴线zn；yn轴方向与on-xnzn垂直；建立关节坐标系oi-xiyizi。

图2 相邻连杆坐标系

连杆各参数定义如下：

θn+1为轴xn绕zn轴旋转θn+1度后，与轴xn+1平行。

dn+1为关节偏移，即轴zn上两条相邻的公垂线an、an+1之间的距离。

an为连杆名义长度,即轴zn-1与轴zn公垂线的长度。

αn为扭角，即轴zn-1与轴zn之间的角度。

根据矩阵右乘运算法则，相邻两坐标系之间位置和姿态由前向后的通用变换矩阵为：

(1)

根据图1得机械臂D-H参数如表1所示。

表1 D-H 参数表

1.3 机械臂运动学求解

为了求出机械臂末端执行器相对于固定坐标系o0-x0y0z0的位置和姿态，需建立机械臂的运动学方程。在该六自由度机械臂的坐标系变换中，根据D-H坐标系和D-H参数表，得6个变换矩阵依次为：

通过依次右乘变换矩阵可实现相邻坐标系之间位置和姿态变换，所以机械臂末端执行器坐标系相对于固定参考坐标系o0-x0y0z0变化矩阵为：

(2)

2 RBF神经网络轨迹规划

在直角坐标系中对机械臂末端执行器位置和姿态对时间进行的规划称作笛卡尔空间轨迹规划[9]，在笛卡空间对机械臂末端执行器运动轨迹规划，是为了确保各关节的位置、速度函数图像在运行过程中为光滑曲线[4]。如图3 所示，在空间有无数条曲线可通过A，B，C三个点，在实际的生产过程中，要考虑生产现场条件、效率等因素，因此需要在笛卡尔坐标空间对机械臂末端执行器进行轨迹规划。

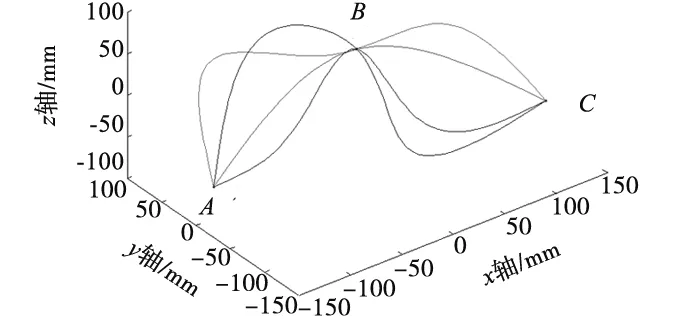
图3 空间路径点

2.1 RBF神经网络模型

RBF神经网络即径向基函数网络(Radial basis function network，缩写为:RBF network)，是一种使用径向基函数作为激活函数的人工神经网络[10]。如图4所示，RBF神经网络是一种三层前向网络。

图4 RBF神经网络

第一层为输入层，由信号源结点组成；第二层为隐含层，以径向基函数为隐含层各单元的变换函数，输入层到隐含层为衰减的非负非线性函数，即RBF神经网络隐含层的功能是将低维输入通过非线性函数映射到一个高维空间。然后在这个高维空间进行曲线的拟合；第三层为输出层，对输入信号作出响应，隐含层到输出则是线性变换的函数，即隐含层的信号通过线性的加权求值得到输出层的输出值，其中权值为可调参数ωij。

随机选取J个样本作为RBF神经网络训练集，激活函数选取Gauss径向基函数，表达式为：

(3)

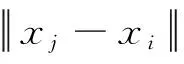
Gauss径向基函数为目前在RBF神经网络中使用最广泛的激活函数，其表达式如下：

(4)

Gauss径向基函数图像如图5所示。其中σ为隐藏层中核心函数的平均偏差，横轴就是到中心的距离用半径r表示，当距离等于0时，径向基函数等于1，距离越远衰减越快，选择性就越好。

图5 Gauss径向基函数图像

RBF神经网络的结构可得输出函数表达式为:

(5)

其中，j=1,2,···,n;n为输出样本数或分类数。

2.2 RBF神经网络学习

在RBF神经网络中，主要的学习参数分别为基函数中心、方差和权值，学习过程分为两个步骤：首先是通过无监督学习，确定隐含层的中心和方差，其次是通过有监督的学习，确定隐含层到输出层的连接权值。

常采用K-均值聚类算法确定隐含层的中心，设xi(n)(i=1,2,···,I)是第n此迭代时基函数的中心，其算法流程如图6所示。

图6 K-均值聚类算法流程图

RBF神经网络的基函数为高斯函数时，方差可由下式求解：

(6)

式中，dmax为所选取中心之间的最大距离；h为隐层节点的个数。

隐含层至输出层之间神经元的连接权值可以用最小均方误差LMS直接计算得到，计算公式如下：

w=φ+d

(7)

公式中d=[d1,d2,···,dn]为期望响应。

φ+为伪逆矩阵，其表达式为：

φ+=(φTφ)-1φT

(8)

矩阵φ为：

φ={φqi}

(9)

(10)

xq为第q个输入向量。

3 仿真分析

为了验证所提出的轨迹优化方法是否有效可行，通过80步圆弧插补进行仿真实验，得到机械臂末端执行器在笛卡尔空间的仿真轨迹如图7所示。由图7可看出末端执行器能从起始点A(60，-120，0)连续运动到终止点B(33，230，0)，证明了此次路径规划的合理性。

图7 仿真轨迹

为了更直观显示机械臂各关节角度随时间的变化关系，图8a表示了各关节角随时间的变化情况；图8b表示了各关节角速度随时间的变化情况，起始速度和终止速度都为零、且速度曲线平滑无突变和拐点，表明机械臂末端执行器运动过程平稳。

(a) 各关节角度曲线

(b) 各关节角速度曲线图8 各关节角度和角速度曲线

将获得的运动轨迹取时间间隔为0.1 s离散转换后，在笛卡尔空间得到一系列路径离散点，采用圆弧插补算法使末端执行器运动轨迹逼近规划轨迹。利用MATLAB软件中的神经网络工具箱，设计RBF神经网络，通过RBF神经网络优化，机械臂末端执行器运动轨迹误差曲线如图9所示。

图9 各轴误差

由图9可看出：经过RBF神经网络优化后，机械臂末端执行器运动轨迹误差在各轴上的垂直投影均低于±0.4 mm，即末端执行器运动轨迹能趋近于优化轨迹，证明此优化方法精度高。

4 实验验证

为了更直观的验证本文提出的轨迹规划方法是否可行，在新一代柔性机械臂xMate平台上进行了试验。此机械臂的6个关节均由伺服电机驱动，实验过程如图10所示: 确定目标物如图10a所示,由工业摄像头确定抓取目标后，吸盘与目标物在同一竖直线上；抓取目标如图10b所示,在抓取目标时，吸盘吸住目标的上表面；抓取过程如10c、图10d所示,到达终点后将目标物平稳放下。机械臂在整个抓取过程中运动平稳，试验达到了预期的效果，验证了此次将RBF神经网络运用于机械臂轨迹规划的合理性。

(a) 确定目标 (b) 抓取目标 (c) 抓取过程 (d) 到达终点图10 机械臂运动过程

5 结束语

本文研究了机械臂轨迹规划中轨迹偏差问题，通过机械臂运动学求解得末端执行器的位置和姿态；通过仿真实验，得到机械臂末端执行器在笛卡尔空间的仿真运动轨迹；借助MATLAB中的神经网络工具箱设计RBF神经网络，通过圆弧插补轨迹离散点对RBF神经网络训练，得到运动轨迹在各轴上垂直投影的趋近误差均低于±0.4 mm。仿真结果表明此次规划得到的轨迹能满足机械臂末端执行器运动要求，通过实验验证了此次轨迹规划的可行性，对进一步将机械臂运用于实际生产奠定了基础。