基于滑模自适应控制的双关节机械手轨迹跟踪*
2021-07-02杨明博周紫阳
杨明博,周紫阳
(北方工业大学机械与材料工程学院,北京 100043)
0 引言
近年来,随着机器人技术和智能控制技术的不断发展,机械手作为机器人技术和控制技术的载体吸引了众多研究人员的目光[1]。其中双关节机械手是通过两个关节共同协作来进行物体的抓取和移动。双关节机械手具有可靠度高、灵活性强、速度快、处理能力强,工作高效等特点,被广泛应用到医疗和工业生产等领域中[2-4]。
目前针对机械手的轨迹跟踪控制,研究人员提出了不同的控制方法。比较经典的算法有PID控制[5-7]、自适应控制[8-10]、神经网络控制[11-13]、反步控制[14-15]等。在实际应用的过程中,PID算法应用较为广泛,但是PID算法更适合相对简单情况,当被控对象结构复杂时,机械手的轨迹跟踪精度难以得到保证。文献[16]中采用传统PID控制,通过调节PID参数进行移动液压机械手的轨迹跟踪控制,仿真结果能大致追踪到机械手的轨迹。但是此方法的误差较大,并且调节参数需要的时间较长,当控制能量需求较大时也很难满足需求。神经网络控制在针对非线性和不确定系统有着明显的优势,也是较先进的控制方法[17]。文献[18]中运用神经网络控制算法对机械手进行动力学建模,对未知部分进行分析与逼近,最后通过在线建模和前馈补偿来实现对机械手轨迹的高精度跟踪。自适应控制是指系统能够根据环境的变化来调整自身的行为或性能。文献[19]采用自适应控制,通过自动调节不确定项来减小误差,提高控制精度。但是系统的控制性能明显依赖于增益值,要获得更好的性能,就必须使用较高的增益。文献[20]在采用自适应思想设计控制器时,引入在线可调参数,使得控制器能够跟踪所给定的有界参考信号,跟踪误差也能收敛到包含零点的很小邻域内。文献[21]采用传统的滑模控制进行控制器设计,虽然最终滑模控制的切换增益大于不确定项或未建模项的上限,可以实现系统的鲁棒稳定,但是较大的切换增益导致抖振现象的产生,进而导致机械臂在滑模面附近产生振荡,控制精度受到影响。
本文采用滑模自适应控制策略来进行机械手的轨迹跟踪控制,相比其他文章,本文考虑了内部不确定因素的干扰,设计干扰的自适应律并且优化自适应参数,加快了误差收敛速度,提升了机械手的轨迹跟踪精度。最后本文采用模糊控制和PID控制作为对照组实验,仿真结果表明了本文控制算法的有效性和优越性。
1 机械手的动力学模型
1.1 坐标系的建立
描述机械手运动状态最主要的量是位姿,为了描述机械手在同一位置所处的不同状态,一般选择在连杆处建立固定的坐标系,坐标系如图1所示。

图1 机械手坐标系示意图
由图1可知,杆1的质心为m1;杆2和未知重物的质心为m2;杆1长为l1;杆2长为l2;杆1质心到原点的距离记为d1;关节到杆2和未知重物的质心距离为d2;杆1和杆2关节旋转角度分别为θ1和θ2;杆1的转动惯量为I1;杆2和未知重物的转动惯量为I2;γ为杆2和未知重物运动时旋转的角度。
1.2 动力学模型
动力学模型描述了机械手系统控制输入转矩和结构运动之间的关系。本文运用欧拉拉格朗日法来建立机械手的动力学模型。因为拉格朗日力学法只需要提供机械臂的运动速度,而不需要求内作用力,这使得模型在运算中得到简化。通过欧拉拉格朗日法进行运算简化可得双关节机械手的动力学方程描述为如下形式[22]:

(1)
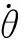
C为哥式力和离心力矩阵,具体表述为:
G为机械臂的重力矩阵,具体表述为:
将自身参数的不确定性表述为α、β、ε、η这4个量。相应的具体表达式为如下形式:
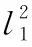
ε=m2l1d2cosγ
η=m2l1d2sinγ
其中,各矩阵中的n1、n2表达式为:
n2=g/l1
2 控制器的设计


设计滑模函数为:
(2)
由于双关节机械手依靠力矩驱动整个系统运动,所以设计控制器时主要进行力矩的设计。设计控制器的表达式为:
(3)
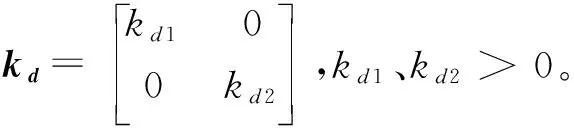
由机械手的动力学特性可知,H是对阵的正定矩阵,并且有界。所以可设计为如下形式的李雅普诺夫函数,具体为:
(4)

τ1、τ2、τ3、τ4均大于0。于是对李雅普诺夫函数进行求导可得:

(5)
将式(3)带入进行运算可得:
(6)
将T的表达式带入进一步运算可得:
(7)

根据机械手动力学方程的线性化特性有:
(8)


(9)
由双关节机械臂动力学模型特性式可知[23]:
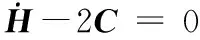
因为sTYPe=PeTYTs,并且sTYPe是对称矩阵,进一步化简得:
(10)
因为本文研究的是内部未知因素对扰动的影响,故以未知量作为自适应律,并且设计自适应律为如下形式[24]:
(11)
所以可得到:
(12)

3 仿真研究分析
根据理论部分的推理结果进行仿真分析。首先是系统基本参数的确定,取机械手的关节1质量为m1=2 kg;杆1长l1为1 m;杆2和未知重物的质量m2=4 kg;杆1质心到原点的距离d1为0.5 m;杆1的转动惯量I1为0.125;关节到杆2和未知重物的距离d2为1 m;杆2和未知重物的转动惯量I2为0.4;将γ设定为0°;关节1的理想运动轨迹为sin3πt;关节2的理想运动轨迹sin2πt;

;kd=50 00 50;λ=3 00 3
仿真结果如图2~图4所示。
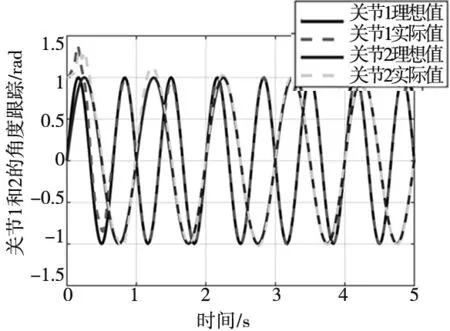
图2 关节1和关节2的角度跟踪

图3 关节1和关节2的角 度跟踪误差图4 α、β、ε、η收敛情况
根据仿真得到的结果进行分析。从图2可以看出,机械手系统的期望运动轨迹能够被稳定跟踪到;图3则反应了跟踪量的误差,可以看出误差在随着时间变化逐渐趋近于0,这反映出了控制器具有不错的跟踪精度。其中关节1在3 s时,角度能够被稳定跟踪到,关节2在3.2 s时,角度能够被稳定跟踪到。通过以上分析可以看出通过运用滑模自适应控制策略设计的控制器能很好的跟踪到期望轨迹,保证了跟踪的精度,证明了这种控制策略的有效性。此外,系统自身未知参数由α、β、ε、η来确定,根据表达式可计算出α、β、ε、η值,分别为α=9.025,β=4.4,ε=4,η=0。为方便进行分析,对这4个量进行归一化处理并进行仿真。根据图4的仿真结果可以看出,这4个量均呈现收敛状态并且收敛速度较快,由此反映出系统的未知参数能够很好的得到抑制,使系统的控制精度得到保证。


图5 模糊控制关节1和 关节2角度跟踪 图6 模糊控制关节1和 关节2角度跟踪误差
根据图5和图6仿真实验结果可以看出,虽然在角度跟踪方面能大致跟踪到理想值,但是误差相对滑模自适应算法较大,并且误差呈现出震荡状态,没有趋近于零的趋势。导致这一点的原因可能是在设计模糊规则及隶属函数时是完全凭经验进行的,而且这种简单的模糊处理会导致系统的控制精度降低和动态品质变差。第二组对照组仿真实验采用PID控制算法,如图7和图8所示。仿真结果可以看出采用PID算法也能很好的跟踪到所设定的轨迹,并且具有较高的精度。但是PID算法在调节3个环节的参数时相对繁琐,如果参数选取的不合适,超调现象相对严重。可以看出,相比PID控制和模糊控制,文本提出的控制策略具有一定的优越性。
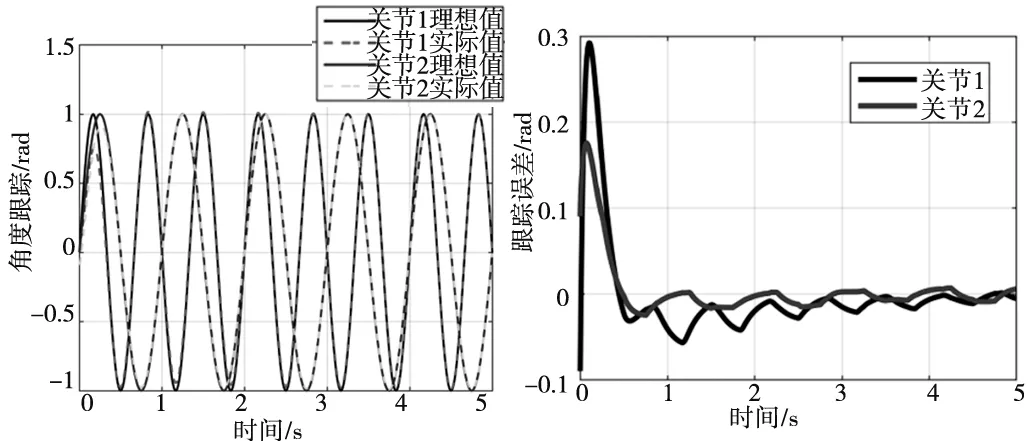
图7 PID算法关节1角度跟踪 图8 PID算法关节1和关节2 角度跟踪误差
4 结论
(1) 提出了一种滑模自适应控制算法,该算法可以在受内部参数的不确定性影响下提高机械手轨迹跟踪精度。
(2) 优化了自适应参数,提高了误差收敛速度和轨迹跟踪精度。
(3) 通过采用模糊控制和PID控制进行仿真对比,证明本文提出的滑模自适应控制算法的优越性。
