基于NGSIM数据的汽车变道越线时间预测

马晨浩，宇仁德，胡婧晖，步玫

(山东理工大学 交通与车辆工程学院, 山东 淄博255049)

从交通运输部发布的《2019年交通运输行业发展统计公报》获悉，截至2019年年底，全国公路总里程达到501.25万km，高速公路总里程达14.96万km[1]，高速扩张的道路网络使汽车出行方式成为首选，然而汽车事故的发生率和死亡人数依然居高不下。变道是驾驶员经常执行的机动操作，由于汽车车速较快且变道过程中周围环境复杂多变，因此发生事故的概率比较高。根据美国道路交通事故的统计数据，在美国，汽车变道所引起的道路交通事故占警方报告的撞车事故的5%、死亡人数的0.5%[2]。如何在复杂的交通环境下高效准确地预测汽车变道是否安全成为了一大难题，而其中越线时间的预测对于汽车变道安全至关重要。对越线时间的研究将为汽车变道安全问题提供一种新的思路和方法，也对辅助驾驶系统和无人驾驶系统的安全性预测有一定的参考价值。

近年来，对于汽车变道行为的研究主要在变道行为分析、变道影响因素、变道决策模型、变道执行模型4个层面。伍淑莉等[3]基于循环神经网络(RNN)和长短时记忆网络(LSTM)的理论研究，提出了一种基于LSTM 的智能车变道行为预测模型。张颖达[4]基于NGSIM轨迹数据建立多项式模型，选取多个误差指标对不同阶数下变道横向移动轨迹拟合效果进行评价，并且分别利用时间对数模型和双隐含层神经网络对变道时间进行预测。王畅等[5]以Jula提出的换道安全性模型为基础，结合营运客车的换道行为特征，通过分析换道进程结束后客车需要与周围车辆保持的安全距离，建立适合于营运客车的换道安全性识别模型，并利用真实数据对模型进行验证，并且从换道轨迹具有相似性的特点出发，建立换道越线时间预测模型。王雪松等[6]基于上海自然驾驶实验采集的驾驶员行为以及车辆运行数据，对比分析不同类型道路上驾驶员的变道特征。Wang等[7]提出了一种基于隐马尔可夫模型(HMM)的两阶段换道模型。Xu等[8]提出了一种基于V2X的驾驶员辅助系统(HM4LCP)的混合式车道变更预测模型。Wang等[9]提出了一种新的基于变道行为的客车变道安全识别模型。Chen等[10]提出了一种基于车辆轨迹数据集的公路车辆变道行为关键特征选择和风险预测的研究框架。综上所述，目前对于汽车变道越线时间的预测研究相对较少，忽视了变道越线时间对于变道安全的影响，因此对于汽车变道越线时间的预测研究有一定的意义。

1 NGSIM数据的处理和筛选

1.1 NGSIM数据简介

NGSIM(next generation simulation即美国联邦高速公路管理局启动的下一代交通仿真工程)数据是为交通微观模拟研究和开发收集的比较详细和准确的现场数据，能够为汽车变道行为的研究提供便利。本文选取I-80路段车辆轨迹数据集为研究数据，监测区域示意图如图1所示，7台同步数码摄像机安装在高速公路旁一栋30层楼的楼顶上(图2)，记录了通过监测区域的车辆。

图1 I-80监测区域示意图

(a)安装在楼顶的数字摄像机 (b)7台摄像机各自的覆盖区域

1.2 变道车辆筛选

为了消除变道微观特性对于后续研究的影响，首先将处于6、7、8号车道内的数据剔除；因为本文选取汽车作为研究对象，所以将摩托车和货车的数据剔除；另外，考虑到汽车车型的影响，仅以中型汽车为标准筛选汽车车长为3.6～4.9 m的数据，上述步骤只需通过Excel即可完成。下一步利用Python编程按照车道发生变换的原则筛选出变道汽车的ID。因为汽车每变换一次车道，程序输出一次ID，且向右变道输出为+1，向左变道输出为-1，所以可筛选出向左且单次变道的汽车(同一辆车在不同时段发生变道只选择一次)共435辆。

1.3 数据平滑处理

为了减弱采集到的原始数据中噪声对于后续模型训练的影响，提高数据绘成曲线的光滑度，采用Matlab中的smooth函数(yy=smooth(y，method))对轨迹数据进行平滑处理。通过对比smooth函数中各种方法的平滑效果，选择移动平均法moving处理汽车的横向坐标和速度数据,选择loess局部回归法(加权线性最小二乘和一个二阶多项式模型)处理汽车的加速度数据，并根据汽车纵向间距与平滑后的横向坐标数据修正每一帧(0.1 s)的车头时距。以40号车为例，横向坐标的平滑处理结果如图3所示。

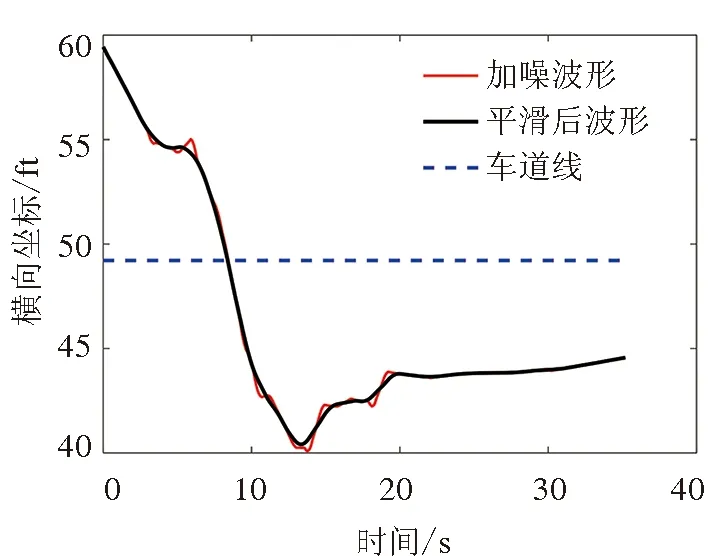
图3 40号车横向坐标的平滑处理图

1.4 汽车单次变道数据提取

本研究以汽车变道过程中横向位置发生单向连续改变所需的时间作为变道持续时间。对于向左变道的汽车，在图3中可直观看到有几段横向坐标连续减小的图像，再根据车道线的位置可以很快判断哪一段是所需的变道数据段。另外，通过观察发现，变道数据段是所有满足条件的数据段中横向坐标变化最大的一段。根据以上原则进行Matlab编程，提取每辆车变道数据的时间点。

以上述时间点为条件，将某辆车变道过程中的数据组提取出来，同时提取邻近车辆的数据，并进行相应的平滑处理，最终得到不同汽车的车组变道总数据。在每组车组变道总数据中按车道发生变换的时间点，将每辆变道车的越线时间作为因变量，选择符合条件的前99组进行后续研究。

1.5 自变量选择

本研究将原车道横向位移量X、汽车变道初始速度v、与原车道前车初始纵向间距ΔY0、与原车道前车初始速度差Δv0、与目标车道后车初始纵向间距ΔY1、与目标车道后车初始横向间距ΔX1、与目标车道后车初始速度差Δv1、与目标车道前车初始纵向间距ΔY2、与目标车道前车初始横向间距ΔX2、与目标车道前车初始速度差Δv2共10个自变量作为变道越线时间的潜在影响因素。统计所有车组变道总数据中以上10个自变量的值对应1.4中相应的越线时间。

2 多元线性回归模型的建立

本文尝试分别利用多元线性回归和多元非线性回归的方法进行拟合并比较，选出一个效果最佳的函数表达式。

由于自变量的个数比较多，因此选择利用Spss软件中逐步回归的方法筛选自变量，其工作原理为：对自变量进行逐个引入，每引入一个变量就对已经引入的所有自变量进行显著性检验；当之前引入的某个自变量不再显著的时候就会对其进行剔除，直至没有任何一个自变量引入或者剔除时为止[11]。得到的多元线性模型为

T=0.432X+0.132Δv0-0.016ΔY2-

0.166Δv2+4.743，

(1)

输出结果见表1—表3。

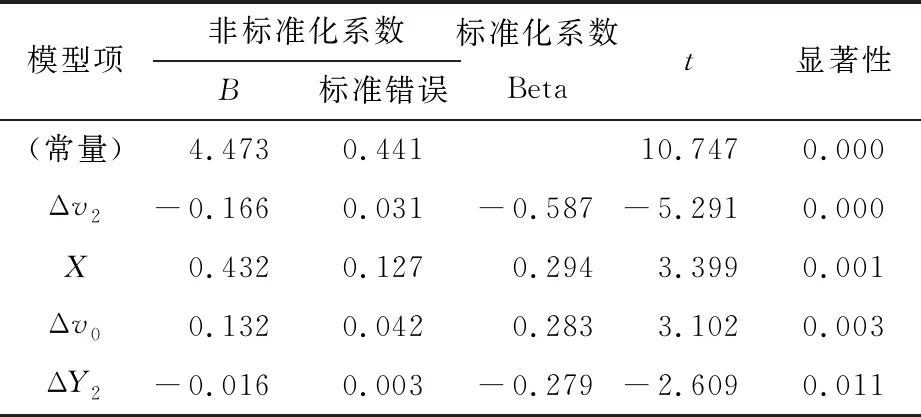
表1 模型系数表

表2 模型摘要

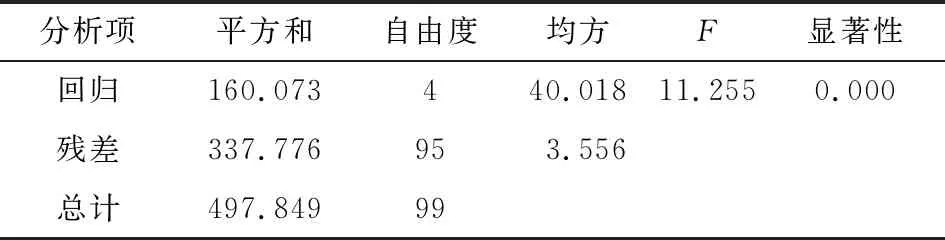
表3 模型方差分析表

从逐步回归分析输出的表2中可以看出，模型的精度为 0.567，说明模型的拟合效果较差。但从表3中可以看出，显著性为0.000，小于假设的显著性水平0.05，表明模型的线性关系仍显著，模型具有实际意义。从表1的模型系数表中可以发现，各个系数的显著性值均小于0.05，表明自变量的系数均显著大于0，从而模型仍可用于对变道越线时间的预测。

3 多元非线性回归模型的建立

3.1 灰色关联度分析

鉴于多元线性模型的拟合优度较低，从物理学角度分析发现，逐步回归模型剔除的某些自变量实际上可能对变道越线时间的影响较大，导致模型在预测上出现较大的偏差。例如，汽车变道初始速度v从实际经验上看对变道越线时间一定会产生较大的影响。为了对变道越线时间进行更精确的预测，下面通过灰色关联度分析判断各个自变量对因变量的影响程度，找出影响程度最高的自变量。

3.1.1 自变量的无量纲化

为了排除自变量之间单位不同对机理模型描述客观规律的影响，使用标准化方法将原始数据组标准化为均值为0、方差为1且接近于正态分布的数据组。标准化方法的公式如下：

Xi′(k)=(Xi(k)-u)/δ

(i=1,…，11；k=1,…，99)，

(2)

式中:i为数据列的列数(1是因变量，2～11为自变量，下同)；k为每组数据列中的数据个数；Xi(k)为因变量和自变量数据列的各个原始数据；u为此变量数据列的平均值；δ为此变量的标准差；Xi′(k)为标准化后对应的数据[11]。

3.1.2 关联度计算

将无量纲化后的越线时间数据列作为参考数据列，其余自变量的数据列分别作为比较数据列，利用下式计算参考数据列和各比较数据列曲线之间的差值大小：

Δi(k)=丨Xi′(k)-X1′(k)丨

(i=2,…，11；k=1,…，99)。

(3)

两级最大差与最小差分别为：

Δ(max)= maximaxkΔi(k)，

(4)

Δ(min)= miniminkΔi(k)，

(5)

则可求得某车参考数据列与比较数据列之间的关联系数为

γiy(k)=(Δ(min)+ρΔ(max))/

(Δi(k)+ρΔ((max))

(i=2，…，11；k=1，…，99),

(6)

式中ρ为分辨系数，其意义在于避免Δi(k)过大而造成的数据失真，用来提高关联系数之间的差异显著性，ρ的取值范围为 0～1，一般取ρ=0.5[11]。

为了对因变量和各自变量进行整体比较，对每列自变量关联系数值求平均值，得到参考数据列与比较数据列之间的关联度。

3.1.3 关联度排序

根据以上步骤进行Matlab编程得到每个自变量与因变量之间的关联度如下:

γ2y=0.725 7，γ3y=0.729 2，γ4y=0.772 8，

γ5y=0.786 9，γ6y=0.749 1，γ7y=0.728 9，

γ8y=0.662 3，γ9y=0.760 6，γ10y=0.752 2，

γ11y=0.765 4。

因此关联度从高到低为：Δv0、ΔY0、Δv2、ΔY2、ΔX2、ΔY1、v、ΔX1、X。

3.2 Pearson相关性分析及曲线拟合

在建立多元非线性模型之前，为了能够筛选出具有相关关系的自变量，减少自变量的个数，对10个自变量进行相关性分析，然后对相关关系较强的自变量进行两两之间的曲线拟合，判断它们之间是否具有对应关系；若有即可通过剔除其中一个自变量，精简自变量个数[11]。

基于所要研究的自变量均为连续型变量，选择Spss中的Pearson相关性分析方法，输出的相关性表见表4(篇幅有限，只截取一部分)。

表4每行中上边的数字代表相关性系数，下边的数字代表显著性系数。从表4发现，ΔY0、Δv0这两个自变量与其他自变量的相关性系数均低于0.4，属于低度线性相关，因此将ΔY0和Δv0作为单独自变量进行非线性回归。另外，有些两两因素之间本就存在一定的关系，例如X0是求解ΔX1时的条件，虽然它们显著性和相关性都比较强，但无需对它们进行曲线拟合(如表中紫色部分)。按照表4，将对v、ΔY2等两两一组的自变量(如表中红色部分)进行曲线拟合。

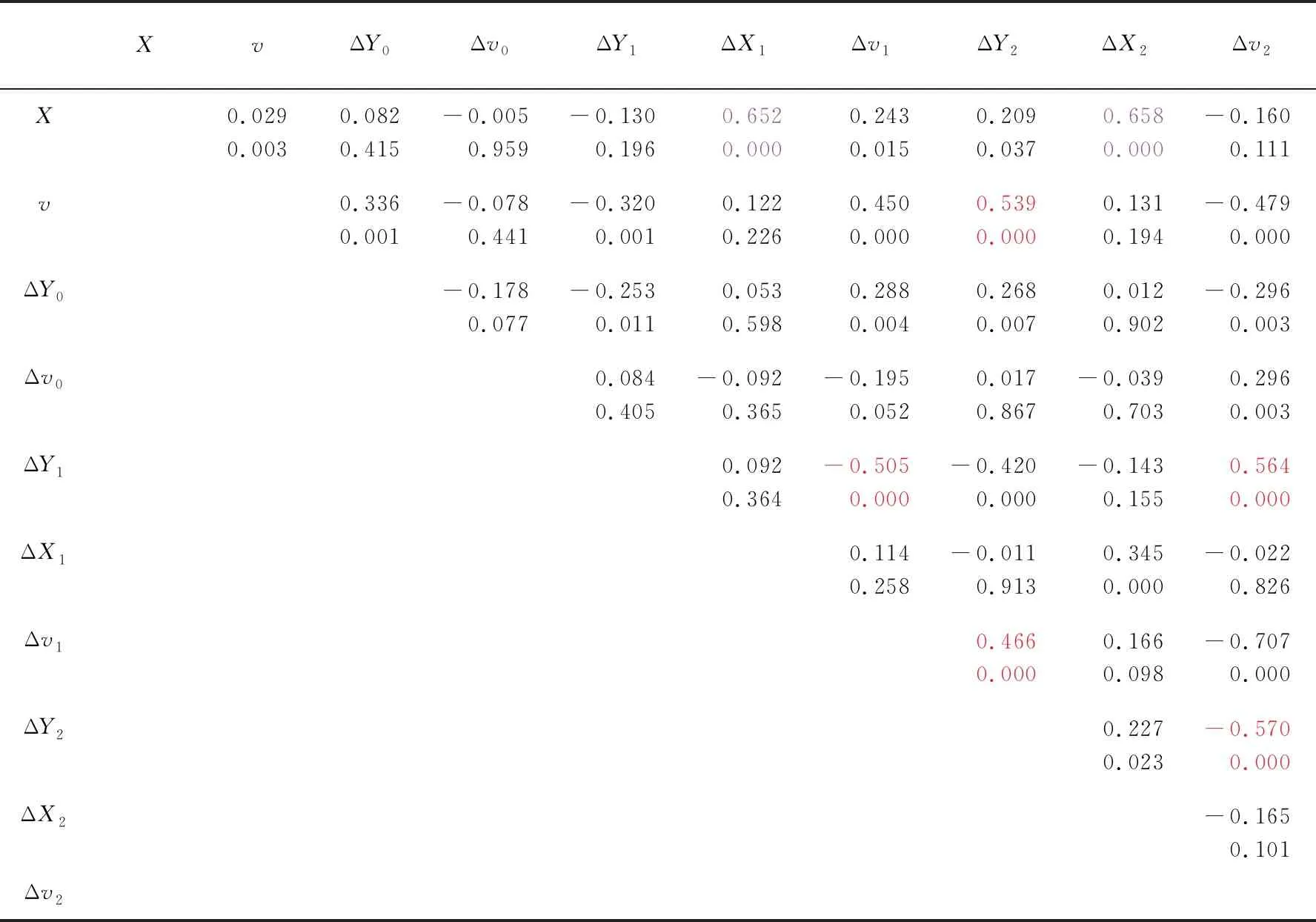
表4 Pearson相关性分析表

本研究采用Matlab中的cftool工具箱来进行曲线拟合。通过不断拟合观察每组自变量之间的函数关系可知，拟合优度R2均在0.5左右，达不到曲线拟合的要求。综合考虑自变量关联度的大小，在对越线时间进行拟合时，应该优先考虑关联度较高的自变量对越线时间的影响。

3.3 模型的建立

3.3.1 数据的处理和筛选

为降低极端数据对训练数据效果的影响，保证训练和测试数据的随机性，将99组数据中越线时间、目标车道变道时间、总变道时间过大或过小的9组数据删除，再将剩余数据按训练数据∶测试数据=2∶1的比例划分，其中测试数据选择中间的30组数据。

3.3.2 确定回归模型

Matlab中的beta=nlinfit(x，y，model，beta0)函数是进行多元非线性回归常用的函数，其中：x为自变量，可以是多个自变量；y为因变量，只能有一个；model是函数模型；beta0是模型系数的初值；beta是求得的模型系数。另外，对于model函数模型，直接使用内联函数model=inline(′y1′,′beta′,′x′)建立，y1是回归模型的函数表达式。

由于没有可供参考的回归模型，只能根据典型的函数模型如幂函数、指数函数、对数函数等不断尝试。10个自变量都与横向距离、纵向距离、速度这3种指标有关，而且在保证拟合效果的情况下，自变量越少,模型的运算速度也会越快;因此,先选择上述3种指标中关联度最高的ΔY0、Δv0、ΔX2作为拟合所用的自变量。经过反复尝试，得到以下3种函数模型表达式可用于数据拟合：

%model1=inline(′beta(1)+beta(2).*

exp(beta(3)./x(:,1))+beta(4).*x(:,2)+

beta(5).*x(:,3)′,′beta′,′x′),

(7)

%model2=inline(′beta(1)+beta(2).*

x(:,1)+beta(3).*x(:,2)+beta(4).*x(:,3)+

beta(5).*x(:,1).*x(:,3)+beta(6).*x(:,2).*x(:,3)′,′beta′,′x′),

(8)

%model3=inline(′beta(1)+beta(2).*

exp(beta(3)./x(:,1))+beta(4).*exp(beta(5)./

x(:,2))+beta(6).*exp(beta(7)./x(:,3))′,

′beta′,′x′),

(9)

对于拟合的效果，采用拟合度指标Rnew来表示，Rnew越接近1,表示拟合效果越好。Rnew的表达式如下：

(10)

式中：y1为拟合越线时间；y为真实越线时间。

求得利用上述3种模型拟合测试数据的Rnew值分别为0.938 2，0.932 2，0.934 4，拟合优度值均接近1。但是通过计算每辆车越线时间拟合误差(y1-y)的大小会发现，这3种模型拟合30组测试数据的误差在[-1,1]的均只在40%左右，在[-0.5,0.5]的更是低于30%。对于越线时间来说，拟合误差在[-0.5,0.5]的拟合效果比较好，由于真实越线时间是从图像中按照一定的规则提取出来的，所以在[-1,1]的拟合误差也可以接受，而超出这一范围的则会对汽车变道安全产生不利影响；因此，排除这3种模型并且重新采用自变量中关联度最高的ΔY0、Δv0、ΔY2、ΔX2、Δv2来进行拟合。同样地，经过反复尝试和测试，得到拟合效果最好且拟合误差较小的函数模型表达式为

y1=6.3829-0.00504.*x(:,1)+0.1355.*x(:,2)-

0.0052.*x(:,3)-0.2668.*x(:,4)-0.1048.*

x(:,5)-0.0082.*x(:,1).*x(:,4)。

(11)

越线时间真实值与拟合值对比图如图4所示，越线时间真实值与拟合值误差如图5所示。(图5中两条绿色虚线是y=0.5和y=-0.5)。

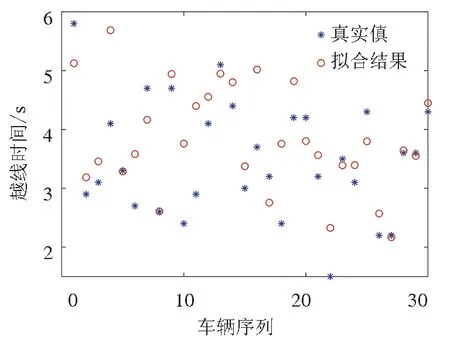
图4 越线时间真实值与拟合值对比图

图5 越线时间真实值与拟合值误差图

利用此模型拟合测试数据的Rnew值为0.981 4，接近于1。从图5中可以看出，30组测试数据的误差在[-1,1]的达到25组，占比83%，且其中绝大部分处于[-0.5,0.5]，在误差为0处上下浮动，拟合效果符合要求。因此，该模型通过了验证，可用于对汽车变道越线时间的预测。

4 结束语

变道越线时间预测是汽车变道主动安全技术的一大关键，本文利用多元非线性回归的方法，构建了一种越线时间预测模型，该模型能够有效预测汽车变道越线时间，预测有效率达到83%。本研究仍有以下不足之处：越线时间是指定规则下提取出的，与实际相比会有误差，影响后续拟合效果；未考虑到驾驶员以及车流量、路面状态、天气情况等因素对越线时间的影响，今后可以做进一步的研究；此外，预测有效率有待进一步提高，以提升模型的实用价值。