L2稀疏超图正则非负矩阵分解的图像聚类算法
2021-07-02陈璐瑶
陈璐瑶
(贵州师范大学数学科学学院,贵阳550025)
0 引言
在计算机视觉、模式识别、数据表示或聚类分析中,低秩矩阵分解是一种非常流行的方法。Lee等人[1]在Nature杂志上发表了非负矩阵分解(NMF)方法就是一种特殊的低秩矩阵分解的方法,与传统的算法相比,NMF避免了出现负元素,从而更具有实际物理意义。后来为了利用潜在的流形结构,Cai等人[2]提出了一种图正则NMF(GNMF)方法,该方法通过构造K-最邻近(KNN)方法来考虑数据点几何结构信息。姜伟等人[3]在图正则非负矩阵分解的基础上添加了L1稀疏约束项,得到更加有效和稀疏的系数矩阵,从而节省了存储空间,提高了分解质量。但是由于L1损失函数的结果更具鲁棒性,也就是说对于异常值更加不敏感,而L2的求解更为简单其解是唯一的。L2相对于L1具有更为平滑的特性,在模型预测中,往往比L1具有更好的预测特性。另外,超图是普通图的推广,适用于处理嵌入高维空间的低维子流形的数据,超图考虑到了数据内部的高维样本间的关系,所以要优于普通图。因此,本文在先前工作的基础上进行改进,现将L2稀疏约束项和超图正则项引入NMF中,提出新的带有L2稀疏约束和超图正则的非负矩阵分解(SHGNMF)方法,来得到更稀疏精确的结果。并在公开数据集上的进行实验,结果表明该算法优于其他相关算法。
1 预备知识
NMF是一种特殊的基于局部特征的矩阵分解方法,它侧重于对元素非负的数据进行分析。给定一个非负矩阵V=[ x1,x1,…,xn]∈Rm×n,V的每一列都是一个多维数据点。
NMF的目的是找到两个非负矩阵W∈Rm×r和H∈Rr×n,使以下目标函数式(1)最小:

为了保持数据集的内在几何结构信息,Cai等人[3]在NMF的基础上提出了以下的目标函数:

2 SHGNMF算法
在这一部分中,提出了带有L2稀疏约束和超图正则的非负矩阵分解算法(SHGNMF),它不仅可以保持数据集的内在几何结构信息,而且更加有效和稀疏,提高分解的质量,得到更精确的结果。接下来将给出更新规则和详细推导过程。

其中λ,β是大于0的常数。目标函数的第二项和第三项分别表示的是超图正则项和稀疏项。LHyper=Dv-B超图拉普拉斯矩阵,并且
下面我们采用交替非负最小二乘方法,可得到式(5)的更新规则。将目标函数重新写成:

根据以上分析,下面给出新算法。
算法1 SHGNMF算法
步骤1 V∈Rm×n,1≤r≤min{m,n,}图正则化参数λ>0,稀疏约束参数β>0,邻域大小k>0;
步骤2随机初始化矩阵W和H;
步骤3根据式(10)、式(11)更新矩阵W和H,直到满足收敛条件时停止;
步骤4输出矩阵W∈Rm×r和H∈Rr×n;
步骤5将此算法运用到图像聚类中,计算聚类性能指标精度(ACC)、归一化互信息(NMI)。
3 收敛性分析
定理1对于W≥0,H≥0,目标函数式(5)在更新迭代规则式(10)和式(11)下是非增的。
为了证明此定理,首先引入辅助函数[6]的定义:
定义1
若G(x,x')满足G(x,x')≥F(x)和G(x,x)=F(x),
则G(x,x')是F(x)的辅助函数。
引理1若G(x,x')是F(x)的辅助函数,则F(x)在更新迭代规则:

下是非增的。
证明:根据定义1和更新迭代规则,有:
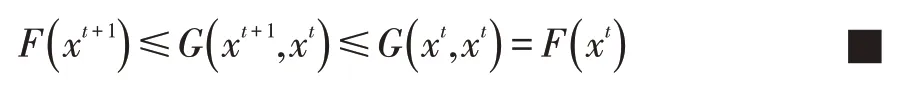
下面证明当辅助函数合理构造时,H的更新规则式(11)与式(12)是一致的。定义Fab是目标函数关于hab对应部分的辅助函数,对Fab关于H求偏导数:
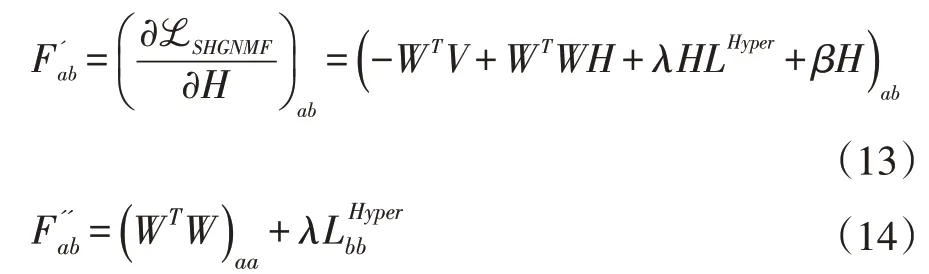
接下来构造关于H合适的辅助函数,为了证明目标函数在更新规则式(11)下是非增长的。
引理2函数


由于式(15)是Fab的辅助函数,所以在更新迭代规则式(20),即式(11)下是非增的。类似地,式(10)同理可证。故而:

4 数值实验
为了验证新算法SHGNMF的有效性,将它与K-means、NMF[1]、GNMF[2]和SGNMF[3]算法进行比较。在ORL和COIL-20数据集上进行实验,并对结果进行对比。文中的所有实验均使用MATLAB 2019a软件进行编程,在处理器型号为Intel Core i5-7500 CPU@3.40GHz 3.41 GHz,系统内存为8.00 GB,64位的Win10操作系统环境下进行的。
4.1 数据描述
ORL:ORL数据集由40个不同对象的400张112×92的灰度人脸图像组成。每个人在不同的时间有10个不同的图像,有不同的灯光、面部表情和面部细节。在实验中,ORL中的所有图像都被调整为32×32。
COIL-20:COIL-20数据集包含对20个物体从不同角度的拍摄,每隔5度拍摄一副图像,每个物体72张图像。总共包含20个对象的128×128大小的1440张灰度图像。在实验中,COIL-20中的所有图像都被调整为32×32。
4.2 参数选择
对于GNMF、SGNMF和SHGNMF,使用p-最近邻方法构造了图拉普拉斯和超图拉普拉斯,其中邻域大小p设为1,图的正则化参数λ设为0.5。
4.3 实验结果与分析
在实验中使用的两个度量标准是精度(ACC)和归一化互信息(NMI),在文献[7]中可以找到详细定义。实施细节如下:
(1)从数据集中随机选取k个类别。
(2)使用SHGNMF算法进行分解得到对应子空间。
(3)使用K-means算法对重构表征进行聚类。
(4)计算ACC和NMI两个聚类指标。
重复上述步骤20次,记录其平均值和方差。表1-表4展示出了ORL和COIL-20数据集的聚类结果。

表1 ORL数据集聚类精度(ACC)

表4 COIL-20数据集归一化互信息(NMI)
由表可知,SHGNMF对比其他相关方法,聚类性能明显提升。其中,聚类精度提升了3.7%~4.5%,归一化互信息提升了1.1%~1.8%。这也表明所提出的新方法是有效的。
5 结语
新方法是基于稀疏约束和超图正则化的非负矩阵分解算法。SHGNMF保留了原始数据中的内部结构,同时,L2范数用于稀疏表示为了防止模型过拟合。在公开的真实数据集上的实验结果表明,SHGNMF得到了更精确的结果,并获得了更好的聚类效果。

表2 ORL数据集归一化互信息(NMI)
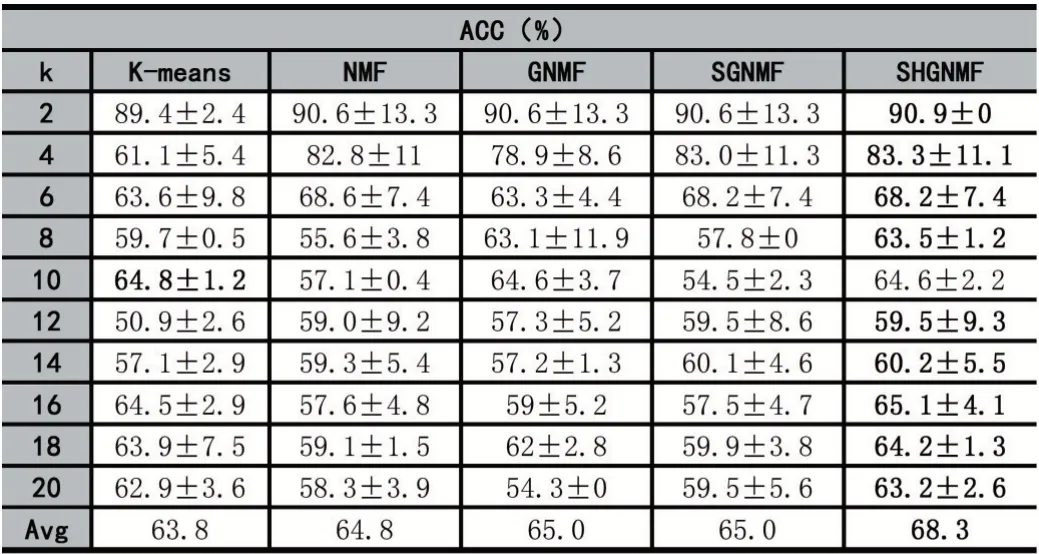
表3 COIL-20数据集聚类精度(ACC)
