一种“π”型补偿管道固定点处轴向推力计算方法

陈 伟

中交第二航务工程勘察设计院有限公司

1 引言

在进行管道设计时须考虑管道的热胀冷缩问题。为使管道在热态或冷态下稳定、安全，减少管道热胀冷缩时产生的应力，管道应考虑设置补偿。管道的补偿可以采用补偿器进行补偿或者利用管道自身弯曲的自然补偿进行补偿。相比于前者，后者不仅更经济，而且无泄漏风险，所以在工程中被广泛采用。管道自然补偿常见的有“L”型和“π”型两种形式，其中“π”型补偿更为常见，典型的“π”型补偿形式见图1。

1.“π”型补偿 2.固定点图1 典型“π”型补偿示意图

管道在两个“π”型补偿之间设有固定点，管道会对该处的固定支架产生轴向推力。轴向推力一般由管道设计专业提供给结构专业，是结构专业进行支架设计的重要依据。轴向推力如果偏大，会导致支架过度设计；如果偏小，则会发生支架被推倒的风险。因此，提出合适的轴向推力尤为重要。

固定支架轴向推力的计算比较复杂，对其计算方法进行系统介绍的相关文献也较少，设计中一般采用计算机进行分析计算。但采用计算机进行分析计算也存在一些弊端，如耗费时间多、不经济，并且在某些情况下不具备进行计算机分析计算的条件，这时就需要一种能够快速方便地计算出管道固定点处轴向推力的方法。

本文系统地介绍了“π”型补偿管道固定点处轴向推力的计算公式和方法，并以两根工程管道为例详细地计算了其“π”型补偿固定点的轴向推力。

2 轴向推力计算分析

固定支架的轴向推力包括管道自然补偿的弹性力(补偿器的弹性力)、由滑动支架传来的摩擦力以及由内压产生的管道补偿器不平衡力等[1]。

一般说来，固定支架所承受的轴向推力是支架两侧轴向水平推力之差，即大小相等、方向相反，但管道开始工作的瞬间，在固定支架两侧温度不同，两侧轴向力之差不能为零。按SH/T3073规定，取0.8的不均衡系数，即两侧轴向水平推力中较大者减去0.8倍较小者，计算模型见图2。

图2 “π”型补偿计算模型图

固定点的轴向推力可采用公式(1)进行计算：

H=Pk1+qμL1-0.8(Pk2+qμL2)

(1)

式中，H为固定点的轴向推力，N；Pk1、Pk2为“π”型补偿的弹性力，N；q为管道单位长度的基本荷载，N/m；μ为摩擦系数，一般为钢对钢，取0.3；L1、L2为两“π”型补偿距离固定点的距离。

由轴向推力的计算公式(1)可知，要计算出固定点的轴向推力，必须知道“π”型补偿的弹性力，而“π”型补偿弹性力的计算很复杂。

文献[2]给出了常见规格管道“π”型补偿弹性力的线算图，图3为“π”型补偿图，图4、图5为DN100和DN500的线算图。通过这些线算图可以迅速查出相应“π”型补偿的最大弹性力，再进行换算和计算，便可快速地求出所求管道“π”型补偿固定点的轴向推力。

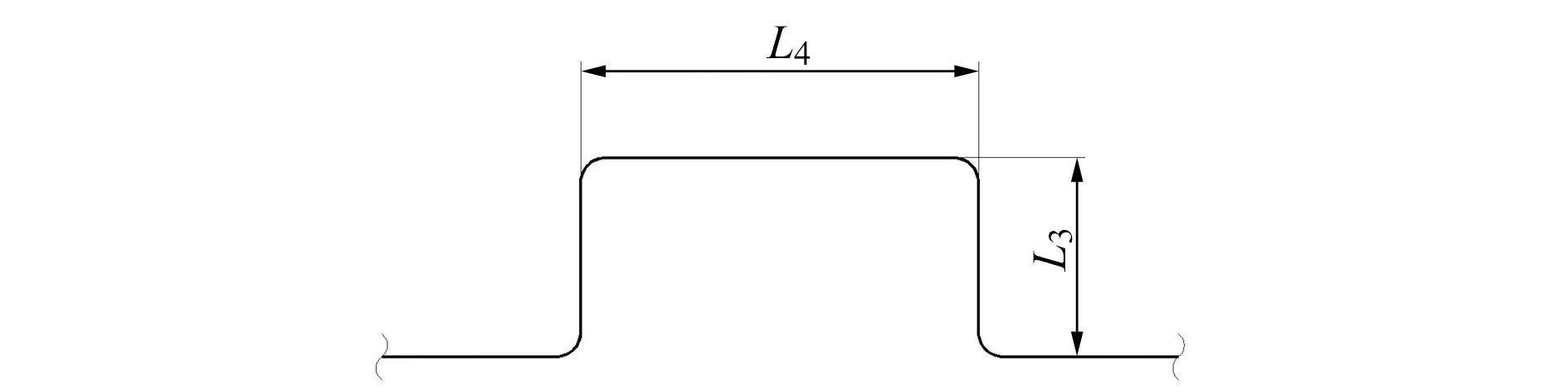
图3 “π”型补偿图

图4 “π”型补偿线算图(无缝钢管：∅114.3×6.02)

图5 “π”型补偿线算图(无缝钢管：∅508×15.09)

文献[2]给出的“π”型补偿线算图是对应管径和壁厚的管道(20号钢，弹性模数为1.926×105MPa)在300℃下的测定值，如果管道的实际运行条件与线算图的给定条件不符，需要进行校正计算才能得出实际运行条件的弹性力(见表1)。

表1 “π”型补偿弹性力换算表

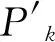
上面换算后得到的“π”型补偿弹性力Pk为以冷态弹性模数100%热胀量计算的弹性力，实际的热态弹性力按式(2)进行计算：

(2)

式中，Ph为“π”型补偿热态弹性力，N；Eh为管材热态的弹性模数，MPa；Ec为管材冷态的弹性模数，MPa。

计算出热态弹性力Ph后，便可由公式(1)计算出“π”型补偿固定点的轴向推力。

热应力许用值σ可按式(3)进行计算[3]：

σ=f(1.25σc+0.25σh)-σ1-σ2

(3)

式中，f为管线伸缩总循环次数，一般情况下取1；σc、σh分别为冷态和热态管材的需用应力，可查相关手册，MPa；σ1、σ2分别为管道因内压和自重作用下产生的轴向应力，MPa。

管道由内压引起的轴向应力σ1可由式(4)进行计算：

(4)

式中，P为操作压力，MPa；D为管道的外径，m；S为管道壁厚，m；C为厚度裕量，m。

管道由自重引起的轴向应力σ2可由式(5)进行计算：

(5)

式中，M为管道的自重弯力矩，Nm；W为抗弯断面系数，m3。

管道的自重弯力矩M可按式(6)计算：

(6)

式中，q为管道的单位长度的基本荷载，N/m；L为管道的跨距，m。

管道的抗弯断面系数W可按式(7)计算：

(7)

3 工程计算实例

某项目有DN100的石脑油管道和DN500的沥青管道各1根，石脑油管道详细参数如下：材质为20#钢，规格为∅114.3×6.02 mm，操作温度为40℃，操作压力为1.0 MPa，石脑油密度为760 kg/m3，“π”型补偿悬臂长L3=8 m，L4=4 m，两“π”型补偿距固定点的距离为50 m，支架跨距为6 m。沥青管道详细参数如下：材质为20#钢，规格为∅508×9.53 mm，操作温度为120℃，操作压力为1.2 MPa，沥青密度为1 220 kg/m3，“π”型补偿悬臂长L3=8 m，L4=4 m，两“π”型补偿距固定点的距离为50 m，支架跨距为6 m。下面根据上述计算方法分别求出这两根管道在“π”型补偿固定点处的轴向推力。

由公式(7)分别求出两根管道的抗弯断面系数W。

=0.526 5×10-4m3

=1.824 6×10-3m3

由公式(6)分别求出两根管道的自重弯力矩M。经计算，石脑油管道的单位长度的基本荷载为218.72 N/m，沥青管道的单位长度的基本荷载为3 391.78 N/m。

=656.16 Nm

由公式(5)分别求出两根管道由自重引起的轴向应力。

由公式(4)分别求出两根管道由内压引起的轴向应力，管道厚度裕量均为0.002 m。

=6.55 MPa

=19.94 MPa

查相关手册知，20#钢管在150℃以下许用应力均为130 MPa，故σc和σh均为130 MPa。由公式(3)分别求出两根管道的许用应力σ。

σ石脑油=(1.25×130+0.25×130)-6.55

-12.46=175.99 MPa

σ沥青=(1.25×130+0.25×130)-19.94-5.58

=169.48 MPa

由图4和图5的“π”型补偿线算图知，DN100和DN500的管道在给定的补偿臂长下最大弹性力分别为0.9 kN和38 kN。由于给定管道的运行温度和管道壁厚与线算图的不一致，需要采用表1的换算公式进行校正，校正后“π”型补偿的弹性力计算如下：

查相关手册知，20#钢在40℃和120℃时的弹性模数分别为1.919×105MPa和1.899×105MPa，由公式(2)分别求出两根管道“π”型补偿的热态弹性力。

最后，由公式(1)可分别求出两根管道在“π”型补偿固定点处的轴向推力。其中，L1=L2=50 m，假定管道“π”型补偿等间距布置，则Pk1=Pk2=Ph，固定点处轴向推力计算如下：

H石脑油=Pk1+qμL1-0.8(Pk2+qμL2)

=0.2(839.44+218.72×50×0.3)=824.05 N

H沥青=Pk1+qμL1-0.8(Pk2+qμL2)

=0.2(22 048.67+3 391.78×50×0.3)

=14 585.07 N

4 结语

通过以上计算可以看出，本文介绍的轴向推力计算方法快速方便。根据线算图可以很快地查出给定“π”型补偿的最大弹性力，再经过换算和计算，便可求出该管道固定点的轴向推力。相比于计算机分析，这种方法更简单快捷，不受客观条件限制。

该种方法也存在一定的局限性，采用这种计算方法需要知道对应规格管道的线算图，而文献[2]只提供了DN40～DN500管道的线算图，并且只有管道材质为20#钢的管道线算图，其他规格或者其他材质的管道暂时无法采用这种方法计算。

对于一般的项目，尤其是前期的项目，可以采用这种方法进行计算，如有必要，可在详细设计阶段再辅助以计算机分析。