基于参考模型的扰动观测器控制系统

周 涛,吴雄林

(洛阳师范学院物理与电子信息学院,河南洛阳 471934)

1 引言

机器人、数控机床、光电稳定平台伺服系统等许多机电系统都可以简化为一个二阶系统,但是由于机电系统的实际建模通常存在一些误差,主要包括模型参数时变和误差、系统的未建模动态以及外部扰动,这些不确定性和扰动会影响系统的实际输出,从而造成控制系统性能下降,甚至造成系统发散.目前,在许多工业应用场合,传统比例积分微分(proportional integral derivative,PID)对存在较大扰动的对象控制效果较差.在一些要求高精度和快速响应的应用领域,PID无法满足高性能控制系统指标的要求.

因此,如何消除被控对象不确定性和扰动的影响,成为控制系统设计者需要解决的首要问题[1].其中,应用扰动观测器补偿是一种重要的方法,通过扰动观测器实时估计系统的扰动量,然后在控制律中进行补偿.在这种方法中,提高扰动观测器的估计精度和实时性至关重要.

在20世纪90年代初,韩京清研究员提出了自抗扰控制技术,近30年来,其工程应用和理论研究不断发展[2].自抗扰控制具有抗扰性能好、鲁棒性强、精度高等优点.目前,已应用于电机控制、火力发电、化工石化、航空航天等控制领域,取得了良好的控制效果,具有较高工程应用价值[1-3].高志强教授将线性自抗扰控制(linear active disturbance rejection control,LADRC)的主要参数分别对应为控制器带宽ωc和观测器带宽ω0,减少了整定参数的数量[4].由于线性自抗扰控制参数调整比较方便,在越来越多的工程控制场合得到应用[2,5].在一些控制场合,自抗扰控制代替了传统的PID,并且控制性能优于PID.自抗扰控制器主要由扩张状态观测器(extended state observer,ESO)、跟踪微分器、状态反馈控制律等组成.其中,扩张状态观测器不仅可以估计系统的状态变量,而且能对作用于对象的总和扰动进行实时观测,从而,在反馈控制律中进行补偿[1].扰动的实时估计补偿能力是自抗扰控制器最本质的特性.因此,ESO是自抗扰控制的核心组成部分.此外,在工程应用中,可以利用ESO进行干扰估计[6]、故障诊断[7]等.文献[1]分析了扩张状态观测器的原理,系统论述了经典自抗扰控制.文献[8]采用反双曲正弦函数设计了一种三阶扩张状态观测器,利用Lyapunov函数证明三阶扩张状态观测器误差系统渐近稳定.文献[9]利用极点配置,设计了一种具有时变参数的扩张状态观测器.文献[10]针对一类非线性不确定系统,构造了一种多变量线性扩张状态观测器,用于实时估计非线性系统的不确定动态.文献[11]为实时准确地观测系统中的未知扰动及状态,提出了一种有限时间线性扩张状态观测器.文献[12]针对受未知干扰影响的一类非线性系统,提出了一种基于滑模观测器和广义观测器的执行器故障和传感器故障估计方法.文献[13]设计了能同时估计系统状态与执行器故障的未知输入观测器,用于传感器的故障诊断.文献[14]在有向图是强连通的条件下,设计了一种基于扰动观测器的分布式算法,实现了存在未知扰动的线性多智能体系统的一致性.文献[15]针对具有未知外界扰动和系统不确定性的四旋翼飞行器,设计了一种模糊不确定观测器,用以估计和补偿未知外界扰动与系统不确定性.文献[16]利用ESO设计了一种输出反馈反推控制,用于补偿液压伺服系统的非匹配建模不确定性.

论文提出一种基于参考模型的扰动观测器控制系统,用于补偿控制系统的总和扰动量.并给出了一种PID参数整定的新方法.首先,分析二阶理想参考模型控制系统的设计,并通过闭环传递函数证明理想参考模型控制系统的稳定性.然后,设计二阶系统扰动观测器和基于参考模型的扰动观测器控制律,分析了二阶闭环控制误差系统收敛性.并推广到n阶系统,进行了n阶控制系统的稳定性分析.最后,进行基于参考模型的扰动观测器控制系统和线性自抗扰控制系统的仿真实验,通过大量的仿真实验对比两种控制系统,以验证新型控制系统的精度和性能.设计的新型控制器调整参数少,结构简单,抗扰性能好,鲁棒性强,扰动估计的精度和控制效率更高,具有重要的工程应用价值.

2 二阶理想参考模型控制系统的设计和稳定性分析

2.1 二阶理想参考模型控制系统的设计

2.1.1 二阶实际系统

对于二阶实际系统

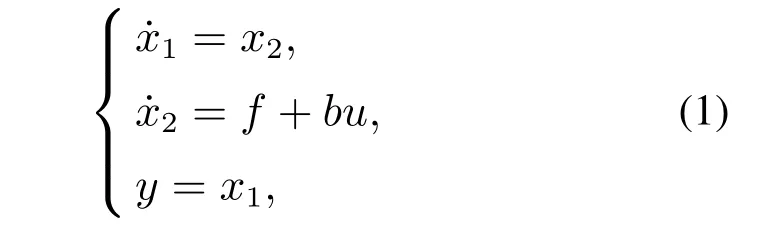
式中:x1,x2为状态变量;系数b ＞0;u为实际系统控制输入量;y为系统输出;f为系统未知的总和扰动量,可记为f(x1,x2,t),它是状态变量和时间的函数,其有界.f包括未建模动态和外部扰动,一阶导数存在且有界.

2.1.2 二阶理想参考模型系统控制器设计

设计系统(1)对应的二阶理想参考模型系统

式中:z1,z2为状态变量,u1为二阶理想系统控制输入量,系统的输出为z1.

假设二阶理想系统(2)的参考输入信号为v,即v为系统(1)的设定输出,取系统(2)的控制输入量为

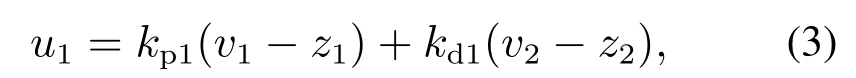
式 中:kp1＞0,kd1＞0,v1=v,v2=˙v.式(3)为PD控制器形式.

2.1.3 二阶理想参考模型系统控制器参数整定

为了方便PD控制器参数的整定和提高系统的响应性能,可以把理想参考模型的闭环误差系统特征方程的极点配置在同一个位置-ωc,即要求控制律的增益满足

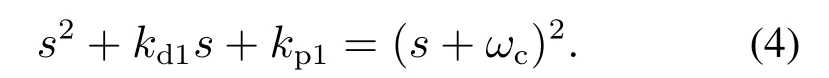
则取系统(2)的控制输入量为

选取ωc的值,使二阶理想系统(2)收敛,即z1→v1,z2→v2=.通过改变ωc的值,可调节系统(2)收敛速度和稳态精度.

2.2 二阶理想参考模型控制系统稳定性分析

定理1对于二阶系统(2),如果控制输入量选择式(3),且kp1=,kd1=2ωc,则二阶理想参考模型闭环系统渐近稳定.

证将式(3)代入式(2)可得二阶理想参考模型闭环系统

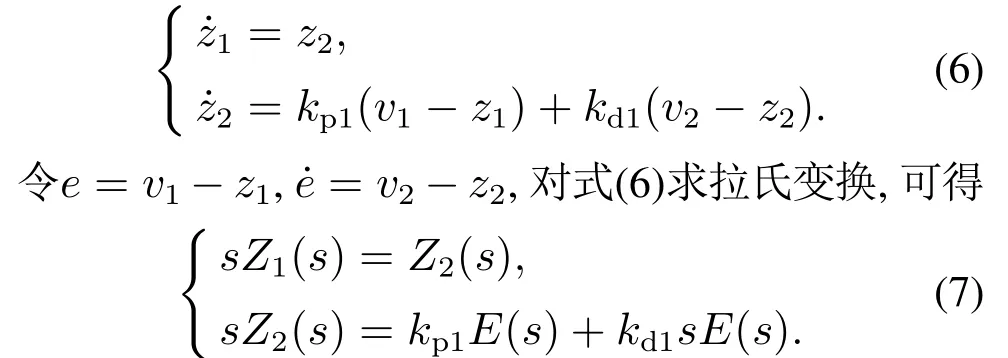
故二阶理想参考模型控制系统的闭环传递函数为

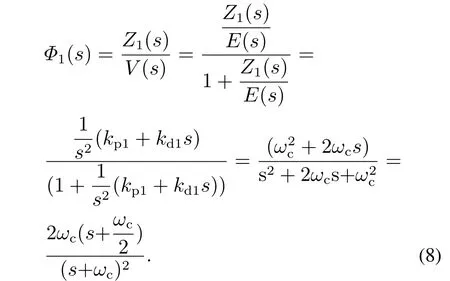
由式(8)可知,二阶理想参考模型闭环系统有2个负实数重极点s=-ωc,此时,二阶闭环系统的阻尼比ξ=1.所以,二阶理想参考模型闭环系统是渐近稳定的,且单位阶跃响应以指数收敛. 证毕.

当二阶系统的阻尼比ξ=1时,系统阶跃响应无超调.为了提高控制系统设计的灵活性,可选择[4]

根据系统性能要求,选择合适的阻尼比ξ值.此外,也可以增加前置滤波器.

3 基于参考模型的扰动观测器控制系统的设计和稳定性分析

基于参考模型的扰动观测器二阶控制系统结构框图如图1所示.

3.1 二阶系统扰动观测器的设计

3.1.1 二阶系统扰动观测器的原理

根据二阶实际系统(1)输出x1与二阶理想参考模型系统(2)输出z1的误差e1,结合控制律u,利用扰动观测器估计实际系统(1)的总和扰动量f.图1中,为扰动观测器的输出.可采用PID控制器,计算简单,实时性高,有利于新型扰动观测器的工程推广应用.该扰动观测器也可以采用其他形式的控制器.

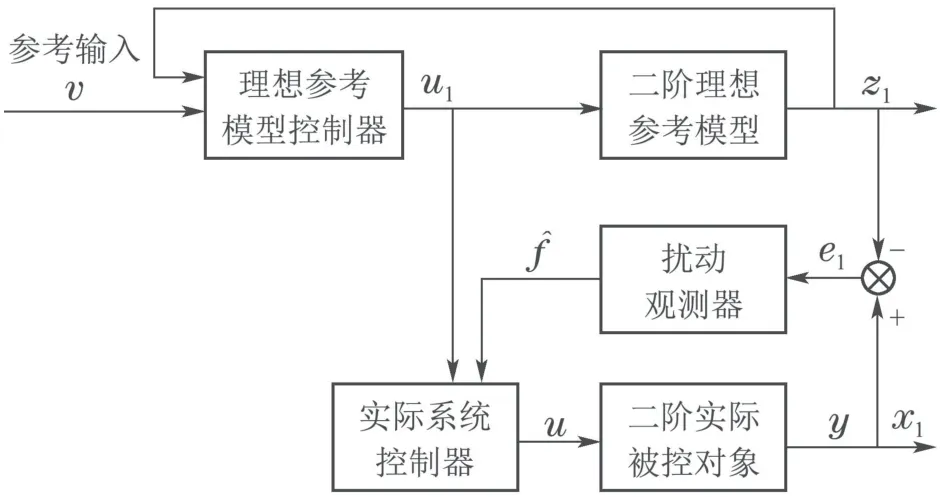
图1 基于参考模型的扰动观测器二阶控制系统结构框图Fig.1 Structure diagram of reference model based disturbance observer second-order control system

令e1=x1-z1,e2=x2-z2=,则由式(1)-(2),可得二阶实际系统(1)与二阶理想参考模型系统(2)的误差系统为

同时,扰动观测器采用PID的形式,取为

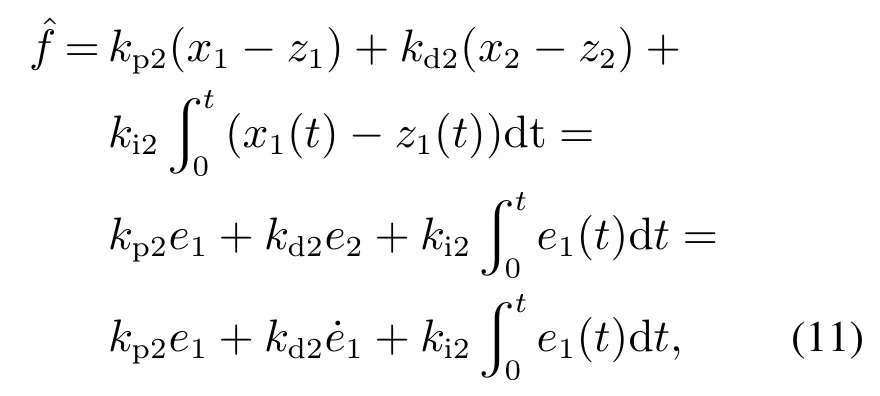
式中:比例系数kp2＞0,微分系数kd2＞0,积分系数ki2＞0.

3.1.2 二阶系统扰动观测器参数整定

为了简化扰动观测器参数的整定,可以把PID扰动观测器系统特征方程的极点配置在同一个位置-ω0,即要求扰动观测器的参数满足

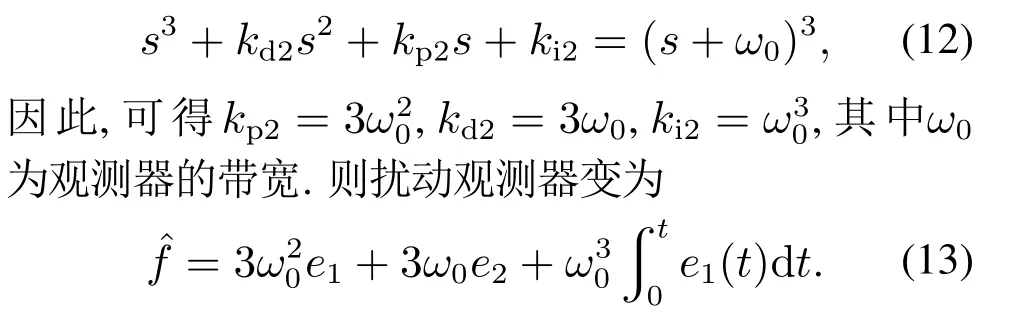
通过合理调整参数ω0,使闭环控制误差系统(10)渐近稳定.

3.2 基于参考模型的扰动观测器二阶系统控制律的设计

为补偿实际系统(1)的扰动作用量f,取二阶实际系统(1)控制输入量u为

将式(5)和式(13)分别代入式(14),可得实际系统(1)的控制律为

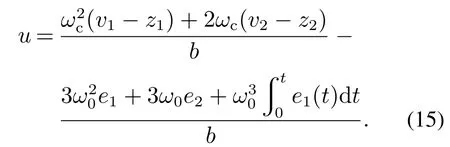
将式(14)代入式(10),则闭环控制误差系统(10)变为

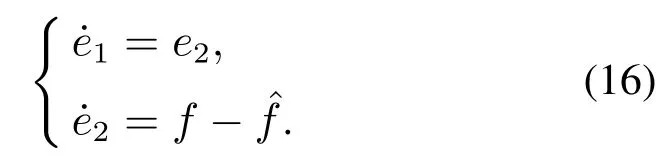
3.3 基于参考模型的扰动观测器二阶控制系统收敛性分析

假设二阶系统(1)的总和扰动量f(x1,x2,t)连续可微,且关于(x1,x2)的偏微分有界,满足下列条件:

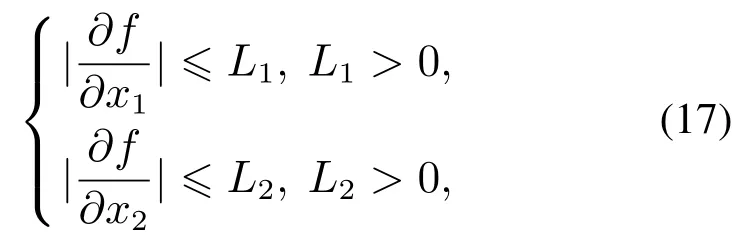
式(17)的条件符合常见的二阶实际系统的工程要求,具有一般性.

同时,式(11)中PID扰动观测器的参数满足如下的公式[17]:

定理2假设二阶理想系统(2)的参考输入信号v为任意的恒定值,对于误差系统(16),如果f(x1,x2,t)连续可微,满足式(17)以及f(x1,0,t)=f(x1,0,0),并且扰动观测器选择式(13),扰动观测器的参数满足式(18),则闭环误差系统(16)收敛于原点,即

3.4 二阶实际系统和二阶理想参考模型系统的关系

当t →∞时,x1→z1,x2→z2,将控制输入量式(14)和式(5)分别代入二阶实际系统(1),则实际系统(1)可转化为

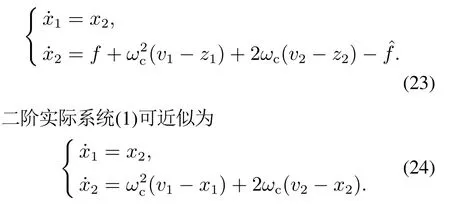
所以,适当调节参数ω0和ωc,可使二阶实际系统(1)近似于二阶理想参考模型系统(2),且以指数收敛,即x1→v1,x2→v2,系统阶跃响应无超调.在一定的范围内,增大参数ωc的值,可以提高闭环系统的收敛速度和跟踪精度.在一定的范围内,增大参数ω0的值,可以提高扰动观测器的估计精度,减小闭环系统的稳态误差.

3.5 n阶控制系统的设计和稳定性分析

3.5.1 n阶实际系统

对于n阶实际系统

式中:x1,x2,···,xn为系统的状态变量;系数b ＞0;u为实际系统控制输入量;y为系统输出;f为系统未知的总和扰动量,可记作f(x1,x2,···,xn,t),它是状态变量和时间的函数,其有界,一阶导数存在且有界.

3.5.2 n阶理想参考模型系统控制器设计

设计系统(25)对应的n阶理想参考模型系统

式中:z1,z2,···,zn为系统的状态变量,u1为理想系统控制输入量,系统的输出为z1.

如果n阶理想系统(26)跟踪的参考输入信号为v,取理想参考模型系统的控制输入量为

其中ωc为控制器的带宽.

3.5.3 n阶系统扰动观测器的设计

取n阶实际系统(25)的扰动观测器形式如下:

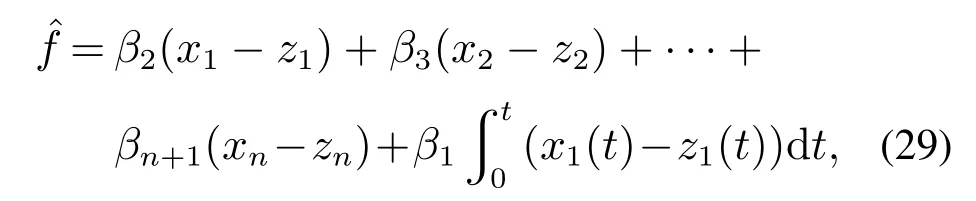
式中参数β1＞0,β2＞0,···,βn+1＞0.

为了简化参数的整定,要求扰动观测器的参数满足下式

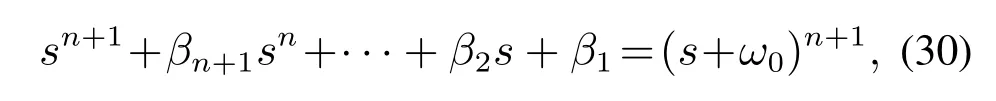
其中ω0为观测器的带宽.

3.5.4 n阶系统控制律的设计

取n阶实际系统(25)的控制输入量u为

3.5.5 n阶控制系统的稳定性分析

将n阶实际系统式(25)减去n阶理想参考模型系统式(26),并由式(31)和式(29)得到n阶误差系统

合理选择n+1个参数β1,β2,···,βn+1,可实现矩阵A为赫尔维茨稳定(Hurwitz).

由矩阵A的Hurwitz稳定性,则对于任意给定的对称正定矩阵Q,存在对称正定矩阵P满足如下的李雅普诺夫方程:

4 仿真实验

设二阶实际系统(1)如下:

式中参数b=5.在系统(42)中,f取为

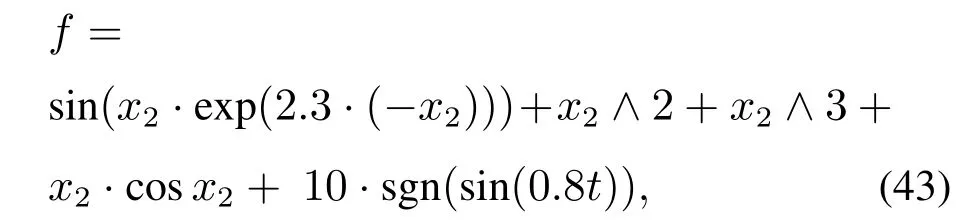
式中:sgn(·)为符号函数.其中10·sgn(sin(0.8t))为外部扰动,其余4个函数为系统内部扰动.

下面,进行基于参考模型的扰动观测器二阶控制系统和二阶LADRC系统的对比仿真实验.

式(11)ˆf为实际系统(1)的总和扰动量f的估计值.通过PID形式的扰动观测器可估计二阶实际系统(1)的总和扰动量.LADRC的扩张状态观测器根据控制输入量和系统输出估计系统的实时扰动量,一方面它估计系统的状态变量,另一方面估计系统的实时扰动量,即被扩张的状态变量[1].

4.1 两个控制系统参数值相同时的阶跃响应对比仿真实验

4.1.1 参数b准确时的仿真实验

二阶LADRC系统主要包括三阶线性扩张状态观测器和PD状态反馈控制律两部分.根据式(12)的方法,三阶线性扩张状态观测器的3个参数整定对应于带宽参数ω0.根据式(4)的方法,PD状态反馈控制律的参数整定对应于带宽参数ωc.当参数b准确已知时,即b=5,基于参考模型的扰动观测器控制系统和LADRC系统的两个可调参数均为观测器带宽ω0和控制器带宽ωc.

取两个控制系统的参数均为ω0=35,ωc=5,b=5.基于参考模型的扰动观测器控制系统阶跃响应输出和LADRC系统阶跃响应输出对比如图2所示,基于参考模型的扰动观测器控制系统扰动的估计信号如图3所示,LADRC系统扰动的估计信号如图4所示,两个系统控制输入量的对比如图5所示.图2表明,基于参考模型的扰动观测器控制系统阶跃响应速度快、无超调、跟踪精度高、抗扰性能好;在控制参数值相同的情况下,LADRC系统阶跃响应跟踪性能较差,扰动造成的输出误差也较大.对比图3-4可知,在控制参数值相同的情况下,基于参考模型的扰动观测器控制系统扰动的估计精度较高.图5表明,基于参考模型的扰动观测器控制系统控制输入量小于LADRC系统的控制量,而且LADRC系统控制输入量出现较大的峰值.上述实验表明,当参数b准确时,在相同的控制参数下,基于参考模型的扰动观测器控制系统的跟踪精度和抗扰性能明显优于LADRC系统,其控制输入量较小.

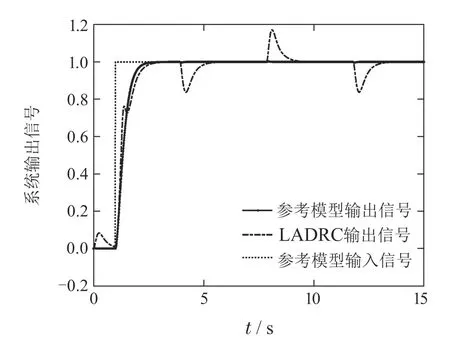
图2 两个系统阶跃响应输出的对比Fig.2 Step response output of two systems

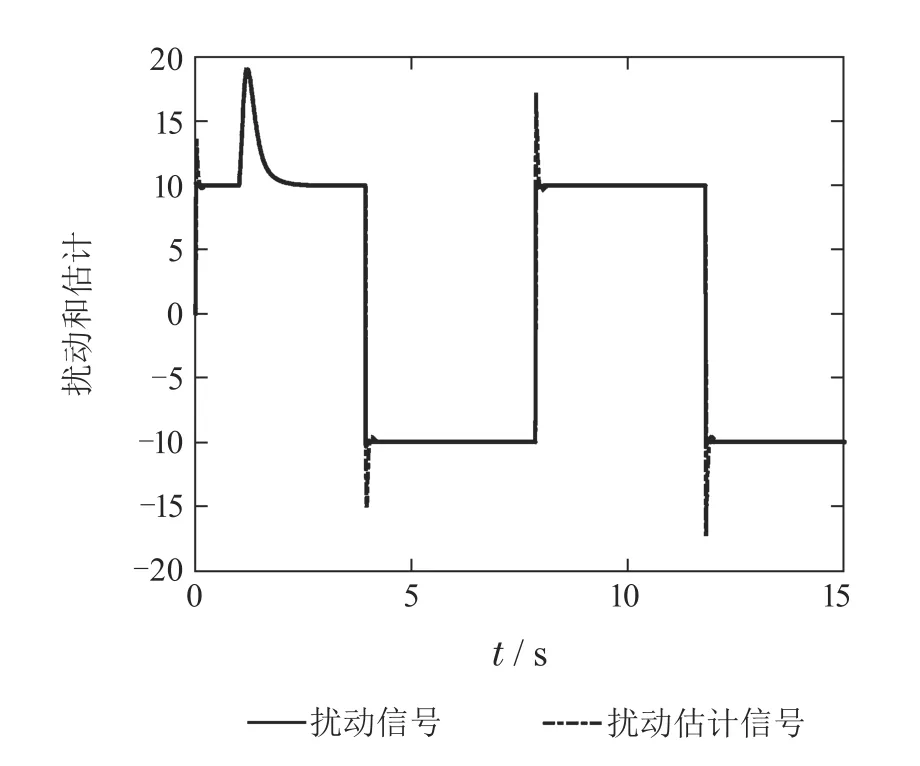
图3 基于参考模型的扰动观测器控制系统扰动的估计Fig.3 Disturbance estimation of reference model based disturbance observer control system

图4 LADRC系统扰动的估计Fig.4 Disturbance estimation of LADRC system

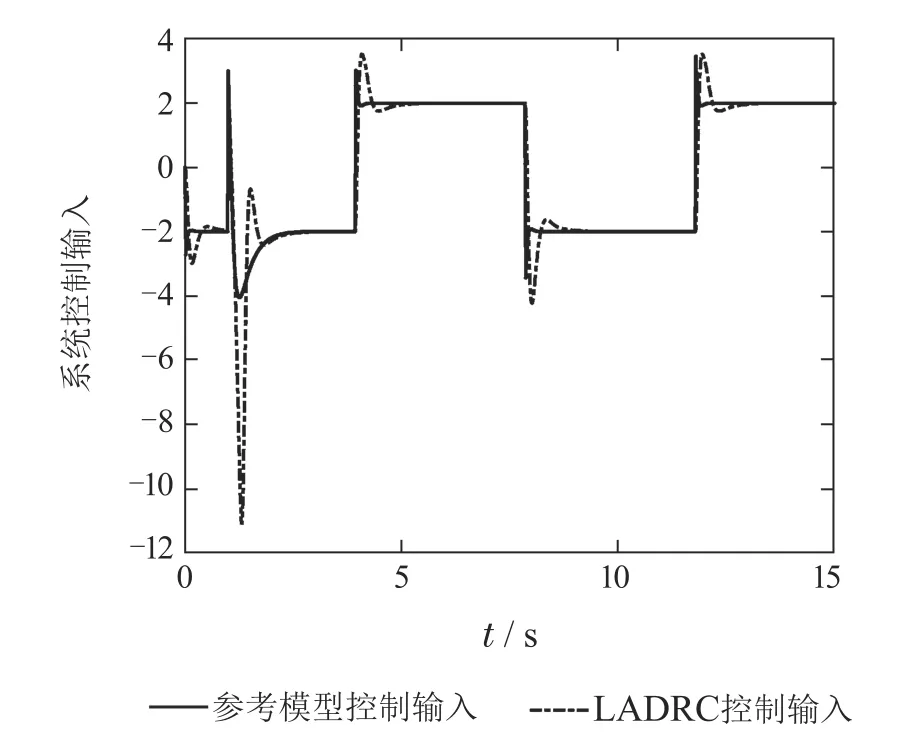
图5 两个系统控制输入量的对比Fig.5 Control input of two systems

4.1.2 参数b不准确时的仿真实验

通常,在工程应用中,二阶实际系统的参数b无法精确获得,假设b的估计值比其真实值小40%时,即取b=3.取两个控制系统的参数均为ω0=25,ωc=5,b=3.则基于参考模型的扰动观测器控制系统阶跃响应输出和LADRC系统阶跃响应输出对比如图6所示,两个系统的扰动估计误差对比如图7所示,两个系统控制输入量的对比如图8所示.图6表明,在控制参数值相同的情况下,基于参考模型的扰动观测器控制系统阶跃响应速度快,无超调,跟踪精度高,抗扰性能好;LADRC系统阶跃响应跟踪精度较差,扰动造成的输出误差也较大.由图7可知,由于参数b存在较大的误差,影响了基于参考模型的扰动观测器和LADRC的扩张状态观测器估计精度,在控制参数值相同的情况下,基于参考模型的扰动观测器控制系统扰动的估计精度较高.图8表明,基于参考模型的扰动观测器控制系统控制输入量小于LADRC系统的控制量,而且,LADRC系统控制输入量出现较大的峰值.上述实验表明,当参数b不准确时,在相同的控制参数下,基于参考模型的扰动观测器控制系统的跟踪精度和抗扰性能也明显优于LADRC系统,其控制输入量较小,鲁棒性更好.

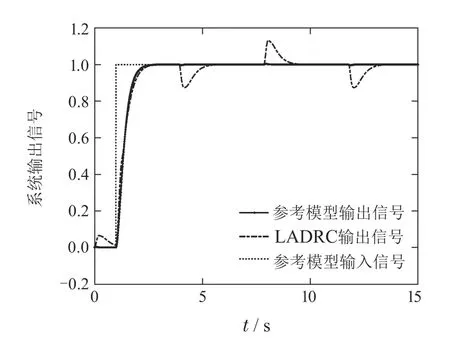
图6 两个系统阶跃响应输出的对比Fig.6 Step response output of two systems

图7 两个系统的扰动估计误差对比Fig.7 Disturbance estimation error of two systems

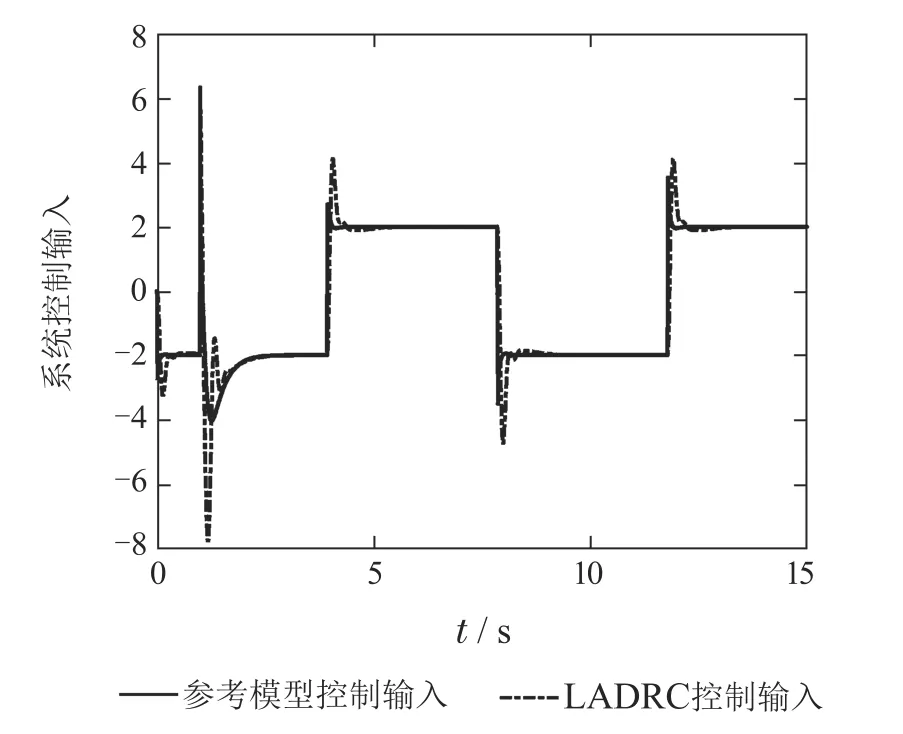
图8 两个系统控制输入量的对比Fig.8 Control input of two systems

4.2 两个系统参数值不相同时的阶跃响应对比仿真实验

为了进一步对比两个控制系统的性能,增加LADRC系统的参数值ω0,以提高LADRC系统的性能,同时,降低基于参考模型的扰动观测器控制系统的参数值ω0,进行对比仿真实验.此时,基于参考模型的扰动观测器控制系统的参数值为ω0=25,ωc=7,b=5;LADRC系统的参数值为ω0=100,ωc=7,b=5.基于参考模型的扰动观测器控制系统阶跃响应输出和LADRC系统阶跃响应输出的对比如图9所示,两个系统的扰动估计误差对比如图10所示,两个系统控制输入量的对比如图11所示.图9表明,与LADRC系统相比,基于参考模型的扰动观测器控制系统阶跃响应的跟踪精度高,响应速度快,抗扰性能也较好.图10-11表明,与LADRC系统相比,基于参考模型的扰动观测器控制系统扰动的估计精度较高,而且,其控制输入量较小.上述实验表明,在LADRC系统的参数值ω0大于基于参考模型的扰动观测器控制系统的参数值ω0情况下,基于参考模型的扰动观测器控制系统的跟踪精度和抗扰性能优于LADRC系统.

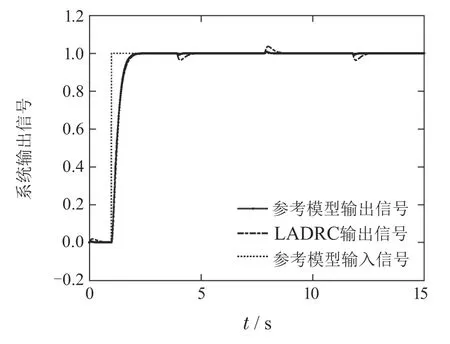
图9 两个系统阶跃响应输出的对比Fig.9 Step response output of two systems

图10 两个系统的扰动估计误差对比Fig.10 Disturbance estimation error of two systems

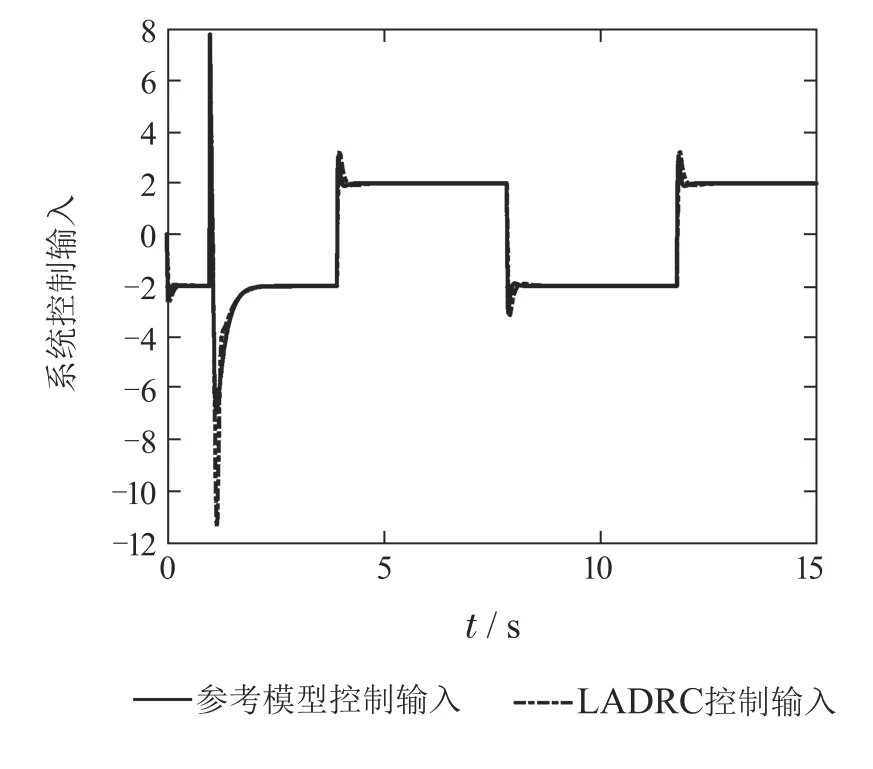
图11 两个系统控制输入量的对比Fig.11 Control input of two systems

4.3 两个系统正弦跟踪的对比仿真实验

假设两个系统正弦跟踪参考输入信号为v=1.0×sin(),角频率为rad/s.取两个控制系统的参数均为ω0=50,ωc=50,b=5.基于参考模型的扰动观测器控制系统正弦跟踪响应输出如图12所示,LADRC系统正弦跟踪响应输出如图13所示,基于参考模型的扰动观测器控制系统扰动的估计信号如图14所示,LADRC 系统扰动的估计信号如图15所示.对比图12-13可知,在控制参数值相同的情况下,基于参考模型的扰动观测器控制系统正弦响应跟踪精度较高,响应速度快,相位滞后较小,抗扰性能更好.对比图14-15可知,在控制参数值相同的情况下,基于参考模型的扰动观测器控制系统扰动的估计精度较高.上述实验表明,在相同的控制参数下,基于参考模型的扰动观测器控制系统的正弦跟踪精度和抗扰性能优于LADRC系统,其扰动估计精度更高.

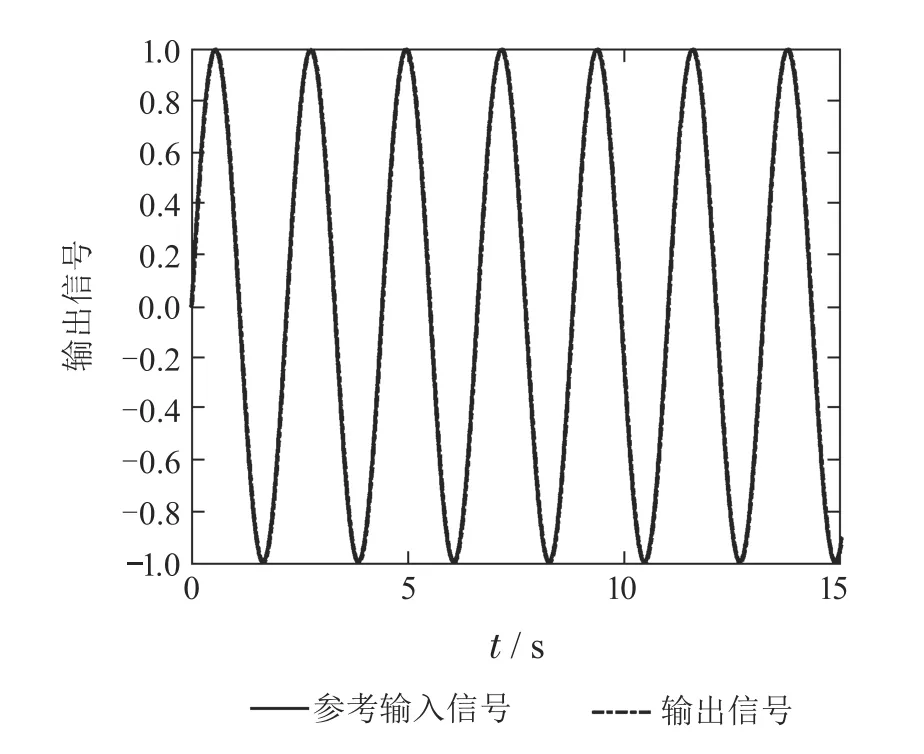
图12 基于参考模型的扰动观测器控制系统正弦跟踪响应Fig.12 Sine tracking response of reference model based disturbance observer control system

图13 LADRC系统的正弦跟踪响应Fig.13 Sine tracking response of LADRC system

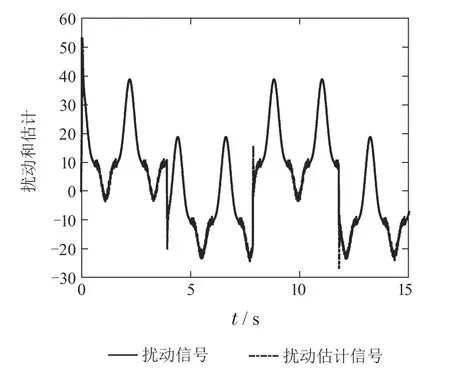
图14 基于参考模型的扰动观测器控制系统扰动的估计(正弦跟踪)Fig.14 Disturbance estimation of reference model based disturbance observer control system(sine tracking)

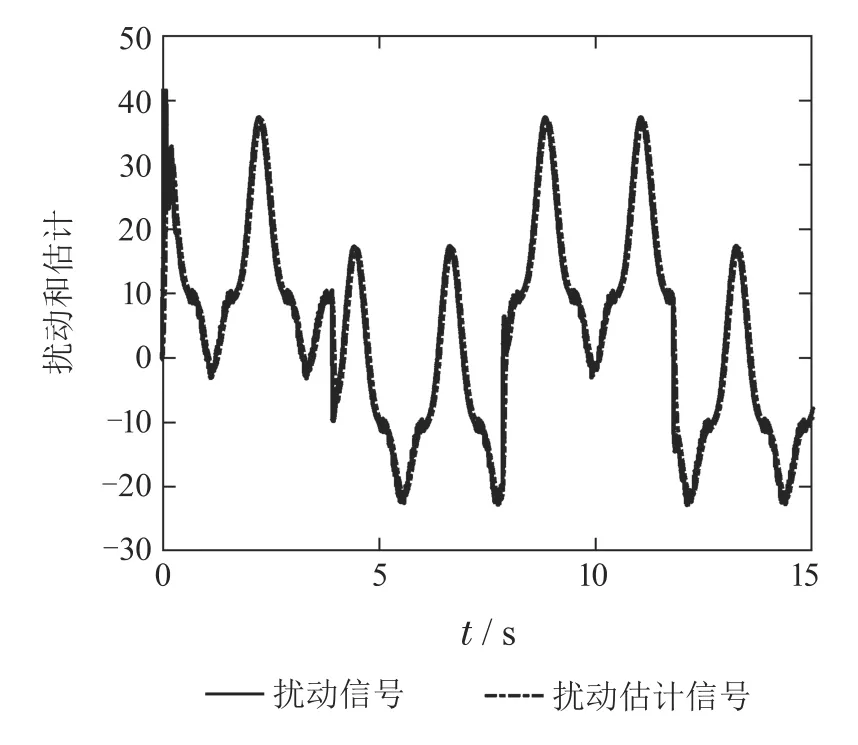
图15 LADRC系统扰动的估计(正弦跟踪)Fig.15 Disturbance estimation of LADRC system(sine tracking)

5 结论

论文提出一种基于参考模型的扰动观测器控制系统,以及扰动观测器和控制器参数整定新方法,并推广到n阶系统.分析了新型扰动观测器和控制系统的原理和设计,并证明了n阶控制系统的稳定性.大量仿真实验表明,在两个系统控制参数值相同,以及在LADRC系统的参数值ω0较大的情况下,基于参考模型的扰动观测器控制系统阶跃响应的跟踪精度和抗扰性能明显优于LADRC系统,扰动的估计精度高,控制输入量小于LADRC系统.此外,当二阶系统的参数b不准确时,基于参考模型的扰动观测器控制系统阶跃响应的跟踪精度和抗扰性能也明显优于LADRC系统.而且,基于参考模型的扰动观测器控制系统正弦跟踪精度和扰动的估计精度也高于LADRC系统.基于参考模型的扰动观测器控制系统的跟踪精度高和抗扰性能好,扰动估计的精度和控制效率高,可广泛应用于机器人、数控机床、三轴转台等精密控制场合,具有重要的工程应用价值.提出的参数整定新方法对于PID控制系统设计具有较高的参考价值.