基于广义超螺旋算法的无速度传感器永磁同步电机有限时间速度控制

张伟键 ,都海波 ,朱文武 ,王利楠

(1.合肥工业大学电气与自动化工程学院,安徽合肥 230000;2.东南大学自动化学院,江苏南京 210096)

1 引言

永磁同步电机由于具有高密度、高效率、高可靠性以及结构简单、体积小、重量轻等优点,已得到广泛应用[1-5].但因为永磁同步电机是一种具有时变参数、强耦合、不确定性和受外部干扰的复杂非线性系统,导致控制系统设计相对复杂.通过磁场定向控制,可以克服永磁同步电机模型复杂性,解耦出电机的转矩和磁通.但磁场定向控制在旋转向量转换时,需要电机转子位子和转速的信息.常用的,如编码器这种速度和位置传感器,增加了系统的复杂性和成本[6].此外,这些传感器容器受到噪声和环境因素的影响,降低了电机驱动的可靠性.

在上述情况下,使用无速度传感器代替机械传感器为一种有效途径.另外,为了保证永磁同步电机在各种环境下正常运行,降低系统成本,无速度传感器近年来已成为研究的热点之一.近年来,国内外学者提出了许多永磁同步电机无速度传感器控制的方法,这些方法按其适用范围可分类两类:1)适用于静止或低速运行时的脉振高频注入法[7];2)适用于高速时的无传感器控制技术,如模型参考自适应法[8]、滑模观测器法[9]、扩展卡尔曼滤波法[10]等.

其中滑模观测器因为其鲁棒性,对参数的不敏感性以及良好的实现性被广泛接受.文献[11-13]将滑模观测器应用在永磁同步电机无速度传感器中.文献[14-15]分别设计了基于滑模无速度传感器的积分滑模控制器和变结构控制器,实现了无速度传感器下的永磁同步电机控制.文献[16]提出了一种新的基于主动干扰抑制的永磁同步电机驱动滑模电流控制方案,增强了对内部干扰的鲁棒性.文献[17]结合非线性扰动观测器,提出了一种新的积分终端滑模控制,所设计的控制器具有良好的动态响应性能和较强的鲁棒性.

为进一步提高滑模观测器精度,不少学者在滑模观测器的基础上,提出了超螺旋滑模算法和广义超螺旋算法.文献[18]根据超螺旋算法设计出的永磁同步电机无速度传感器,相较滑模观测器,具有更快的收敛速度.所谓广义超螺旋算法(generalized super-twisting algorithm,GSTA),是在超螺旋算法上进行改进的,由于加上了线性修正项,使得广义超螺旋算法可以处理系统线性增长的扰动,这是一般超螺旋算法不能做到的.所以,广义超螺旋算法能够明显减少抖振在速度估计的影响,提供改进的稳态和瞬态性能,获得较好的速度估计精度和显著的降噪.但广义超螺旋算法目前尚未应用在永磁同步电机无速度传感器控制上.

本文主要贡献:1)将广义超螺旋算法应用在永磁同步电机无速度传感器,所设计的广义超螺旋无速度传感器,能够精确估计出电机的转子位置和转速.同时,由于有限时间控制系统具有良好的鲁棒性能和抗扰动性能[19-23];2)将有限时间控制理论应用在永磁同步电机无速度传感系统上,所设计的有限时间速度控制器,可以改进传统速度控制器收敛速度慢,超调严重等问题,具有良好的动态性能.仿真和实验结果验证了所设计无速度传感器和控制器的有效性.

2 模型介绍及预备知识

2.1 永磁同步电机数学模型

本文主要研究三相表贴式永磁同步电机的速度调节问题.基于两相静止坐标系αβ,电机的数学模型[24]

其中:iα,iβ为αβ坐标系下定子电流;vα,vβ为αβ坐标系下定子电压;R为定子电阻;L为定子电感;φf是转子磁链;ωm是机械角速度;np为极对数;B为阻尼系数;J为转动惯量;TL为负载转矩;θe为转子位置电角.

永磁同步电机反电动势方程[25]

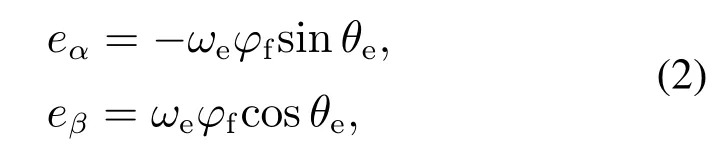
其中:eα为α轴反电动势,eβ为β轴反电动势,θe为转子位置电角,ωe为转子电角速度.

为更好厘清电机中各变量之间的关系,有必要说明:电机的转子位置电角θe、电角速度ωe、转子位置机械角θe、机械角速度ωm、转速Nr关系如下:

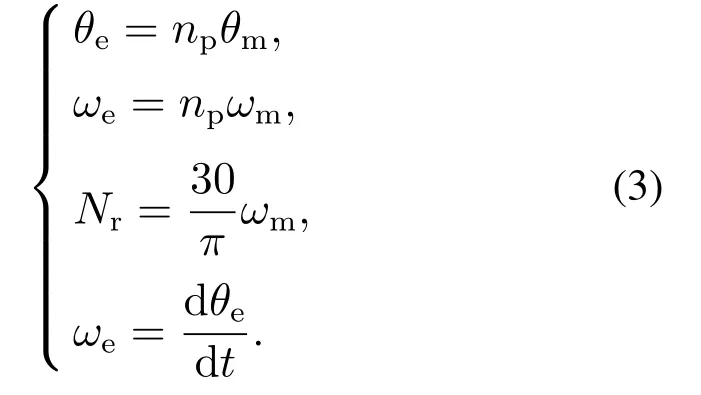
2.2 问题描述

本文的主要目的是利用广义超螺旋算法设计出电机转子位置和速度观测器,用估计出转速作为电机转速反馈信号,设计出有限时间速度控制器.本文提高了无速度传感器的速度估计精度,减少了速度控制的收敛时间.

2.3 相关定义和引理

定义1对于如下系统[26]:

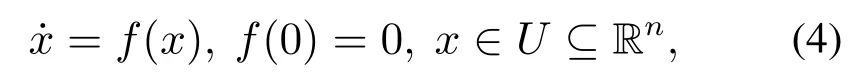
其中f:U →Rn为开区域U上对x连续的函数,且开区域U包含原点.系统的解x=0为有限时间稳定当且仅当系统是稳定的且为有限时间收敛的.所谓有限时间收敛指的是:对∀x0∈U0⊂R,存在一个连续函数T(x):U0{0}→(0,+∞),使得系统(4)的解x(t,x0)满 足:当t ∈[0,T(x0))时,有x(t,x0)∈U0和x(t,x0)=0;当t ＞T(x0)时,有x(t,x0)=0.若U=U0=R,则系统是全局有限时间稳定的.

定义2对于任意0 ≤α≤1,x ∈R,非光滑非线性函数定义如下:

其中sgn为符号函数.

引理1考虑定义1中的系统,假设存在连续可微函数V:U →R满足下列条件[26]

1)V为正定函数;

2) 存在正实数c ＞0和α ∈(0,1),以及一个包含原点的开邻域U0⊂U,使得下列条件成立:则系统有限时间稳定.

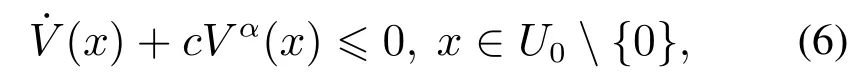
引理2对于如下系统[27]:

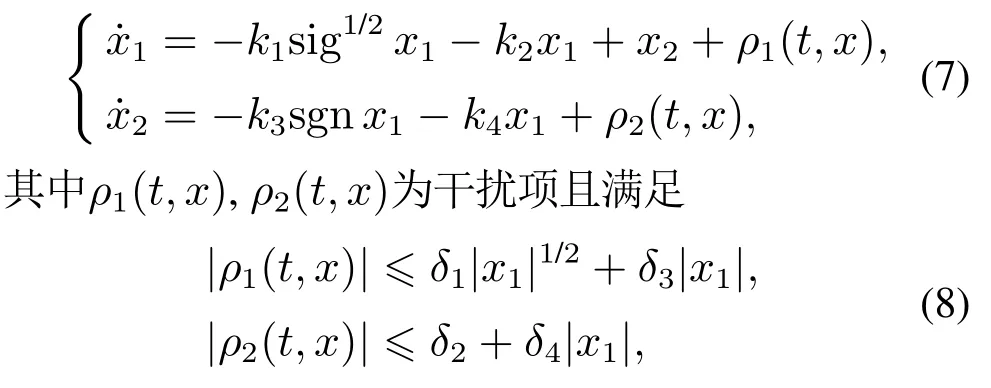
并且δ1,δ2,δ3,δ4≥0,当正的控制增益k1,k2,k3,k4满足一定条件时,则上述系统(7)为有限时间收敛的.具体的证明过程见文献[27].

3 基于GSTA的永磁同步电机有限时间无速度传感器控制器设计

本节首先介绍了基于广义超螺旋无速度传感器的设计.然后,基于上述设计的无速度传感器,设计出有限时间速度控制器.

3.1 基于GTSA的无速度传感器设计

对于永磁同步电机,电压与电流是可测的,反电动势是不可测的.所以,通过设计观测器,估计出电机的反电动势,可估计出电机转子位置和转速.

对于永磁同步电机模型(1)-(2),根据广义超螺旋算法,构造广义超螺旋观测器

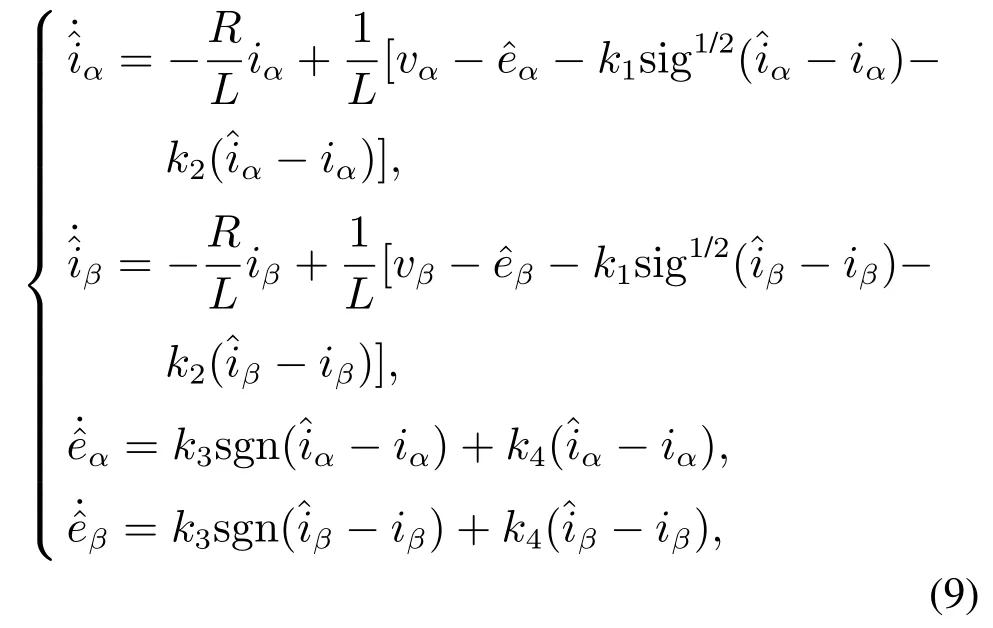
以α轴为例,结合系统(1)-(2)和观测器(9),得到广义超螺旋观测器误差动态方程为

根据广义超螺旋观测器,可以观测出电机的反电动势,而通过反电动势可以进一步估计出电机的转子位置电角、转子点角速度、转子机械角速度等.由式(2)可获得电机的转子位置电角估计公式

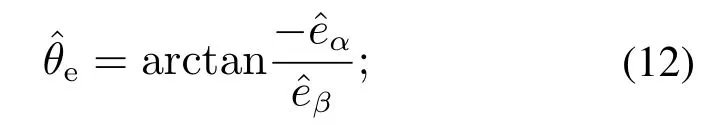
转子电角速度估计值

结合式(3),可得转子机械角速度估计值

图1给出了基于广义超螺旋观测器的转子位置和转速估计的控制框图.

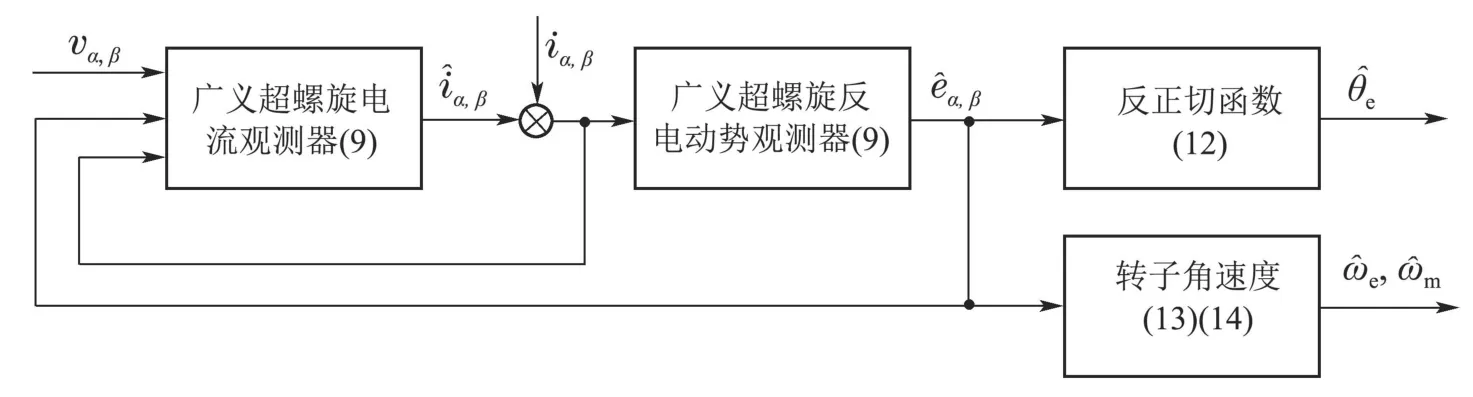
图1 基于广义超螺旋观测器的转子位置和转速估计框图Fig.1 Block diagram of rotor position and speed estimation based on generalized super-twsiting observer

3.2 基于GSTA的有限时间速度控制器设计

基于上节GTSA无速度传感器,本节将给出有限时间速度控制器的设计.首先定义电机机械角速度与期望的机械角速度误差为

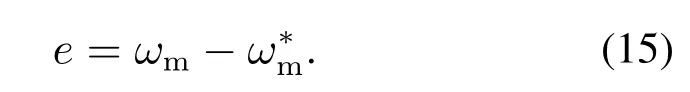
由式(1)得

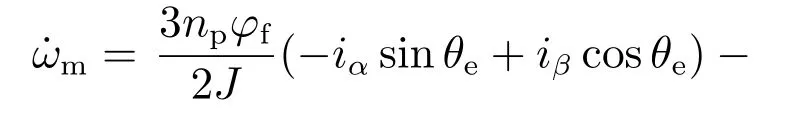
为了实现速度调节,接下来设计基于GTSA无速度传感器的有限时间速度控制器.

定理1对于系统(1),如果速度控制器设计如下:

因此,稳定性分析将分为两个部分,首先证明系统状态在T1+T2时刻之前是有界的,然后证明闭环系统在时间T1+T2之后是有限时间稳定的.

步骤1考虑系统的状态在时间区域[0,T1+T2]的有界性.由于第3.1节设计的无速度传感器是有限时间稳定的,所以下式总是成立的:

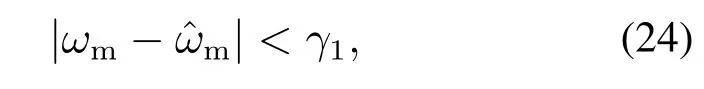
其中γ1＞0.

很明显,上述系统符合广义超螺旋系统设计要求.由引理2可知,上述设计的广义超螺旋干扰观测器ˆd是有限时间收敛的,所以

其中γ2＞0.

取Lyapunov函数

步骤2下面开始分析在T1+T2时刻之后系统的有限时间稳定问题.

结合式(20)-(21)可得

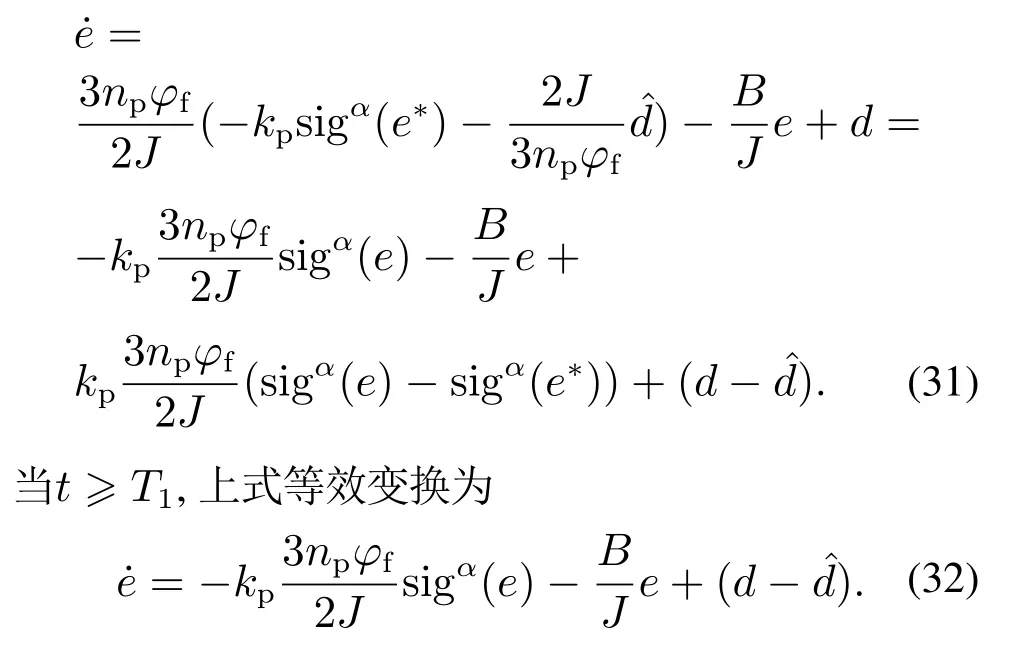
所以,由引理1可知,本文设计的有限时间速度控制器(21)可以保证速度调节系统是渐进稳定并且是有限时间收敛的,即在有限时间内,

证毕.

4 仿真和实验结果

4.1 仿真结果

仿真实验采用Simulink 环境下,搭建整个系统模型,对系统的有效性和稳定性进行了验证分析.Simulink仿真中的步长为2×10-7s.基于GSTA的无速度传感器的有限时间控制器下的永磁同步电机系统框图如图2所示.

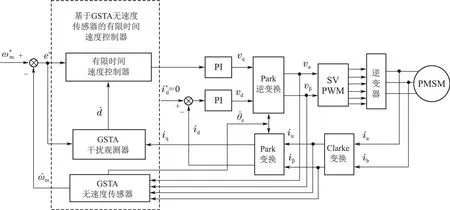
图2 基于GSTA的无速度传感器的有限时间控制器下的永磁同步电机系统框图Fig.2 System block diagram of PMSM under finite-time controller based on GSTA sensorless

在仿真中,永磁同步电机参数值如表1所示.永磁同步电机控制系统仿真中,经反复调试后,各模块参数值如表2所示.

表1 永磁同步电机参数值Table 1 PMSM parameter value

表2 仿真中各模块参数值Table 2 Parameter value of each module in simulation

参考转速设定为Nref=1000 r/min,为了分析负载转矩变化带来的转速变化时的速度跟踪情况,在0.03 s突加负载转矩为TL=10 N.在PI速度控制器下,转子位置跟踪结果如图3所示,转速跟踪结果如图4所示,转速误差比较如图5所示.

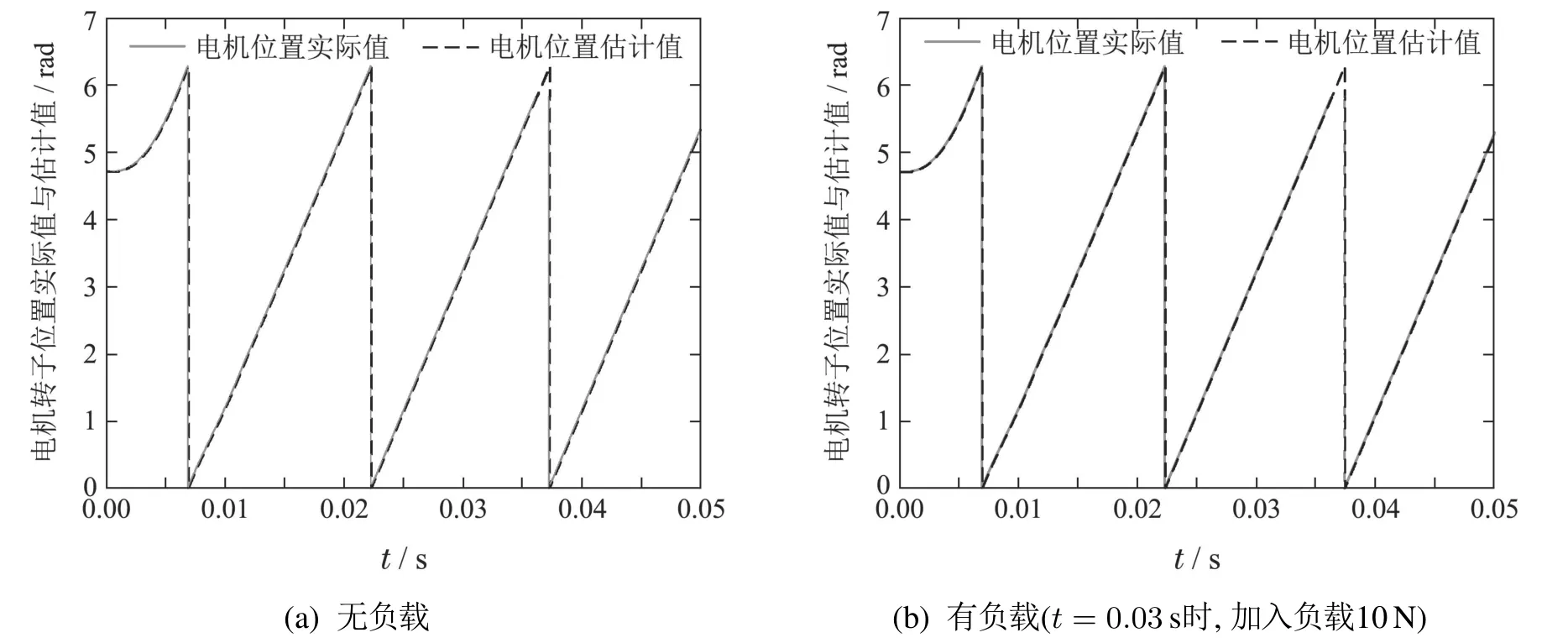
图3 电机转子位置跟踪结果Fig.3 Motor rotor position tracking results

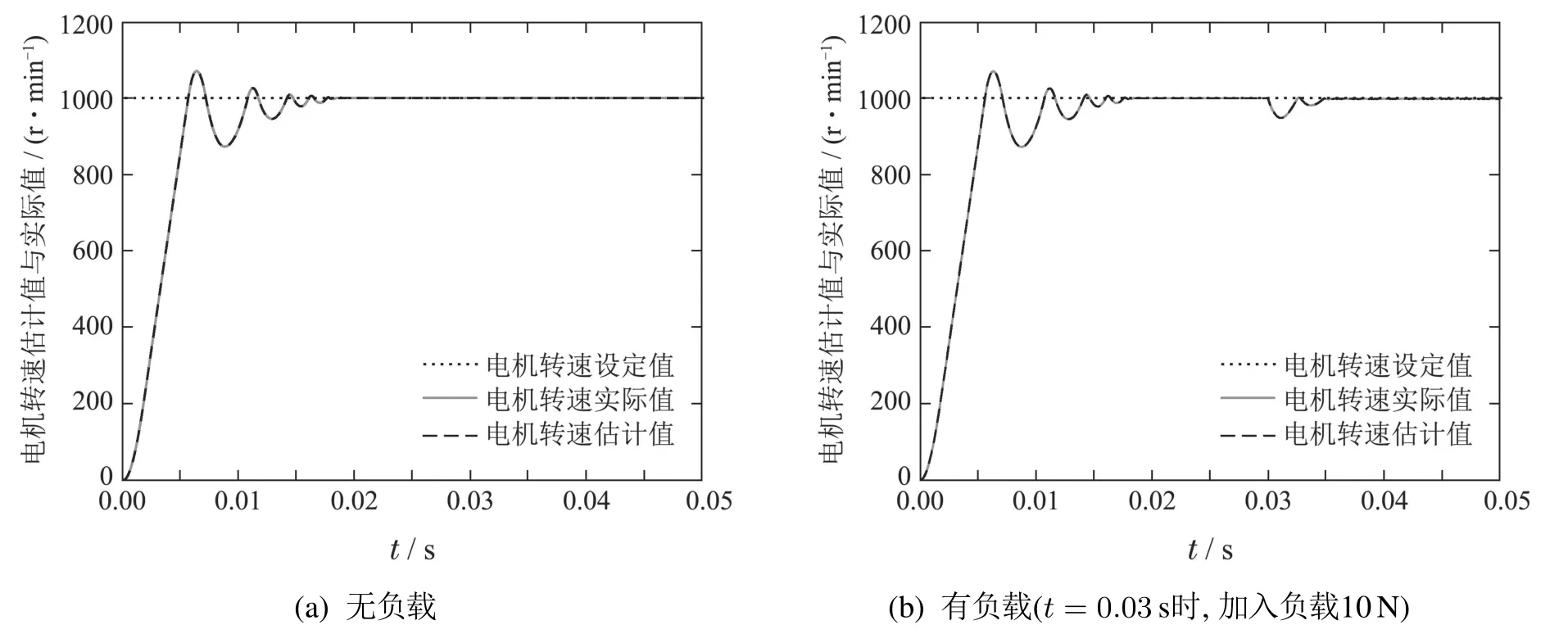
图4 电机转速跟踪结果Fig.4 Motor speed tracking result

图5 电机转速估计误差比较Fig.5 Comparison of motor speed estimation error

从上述结果可知,通过PI速度控制器,在无负载和有负载情况下,所设计的广义超螺旋观测器均能很好地估计电机转子位置与转速,转子位置与转速均能很好地跟踪上真实值;在t=0.03 s处,扰动对电机位置和速度的估计精度影响较小,可以忽略.与传统的基于滑模观测器的无速度传感器,其转速误差达到(-14 r/min～20 r/min);相比之下,基于本文设计的广义超螺旋无速度传感器,其转速误差在(-0.16 r/min～0.21 r/min)之间,可以发现本文设计的方法大大减小无速度传感器了对转速估计的误差.由此可以说明,通过取合适的参数,基于广义超螺旋观测器的三相PMSM无速度传感器能很好地满足电机转子位置和转速高精度反馈的要求.

参考转速设定为Nref=1000 r/min,在0.03 s突加负载转矩为TL=10 N.在广义超螺旋无速度传感器下,有限时间控制器实验结果,如图6所示.有限时间速度控制器各性能对比,如表3所示.实验数据表明,在广义超螺旋无速度传感器下,与传统PI速度控制器实验结果相比,本文设计的有限时间速度控制器超调更小,调节时间更快,动态性能更好.

图6 广义超螺旋无速度传感器下有限时间速度控制器与PI速度控制器对比(t=0.03 s时,加入负载10 N)Fig.6 Comparison of a finite-time speed controller and PI speed controller under generalized super-twisting sensorless(when t=0.03 s,add load 10 N)

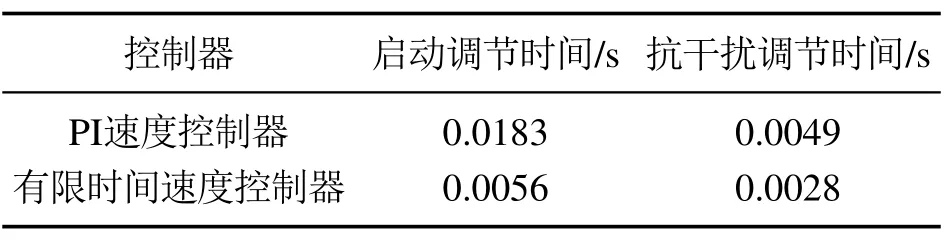
表3 速度控制器性能比较Table 3 Speed controller performance comparison

4.2 实验结果

为进一步验证广义超螺旋无速度传感器与有限时间控制器的性能,下面介绍实验结果.本次实验测装置的配置如图7所示,包括PMSM(埃斯顿公司,型号:EMJ-04APB22),控制器和驱动器,隔离变压器(XH-1000VA),电磁制动器(盛泰科技公司,型号:CD-HSY-50)和张力控制器(KTC800A)等.C代码由具有60 MHz实时时钟频率的数字信号处理器(DSPF28 035)实现.与仿真情况下一样,参考速度为1000 r/min.表4 列出了实验中各模块参数值.实验结果图8 为有限时间控制器(finite-time controller,FC)和PI控制器下电机的真实速度,图9为GTSO对转速估计的误差,图10为FC控制器下抗干扰性能(t=5 s时,加入负载10 N).

图7 实验装置的配置Fig.7 Experimental setup

表4 实验中各模块参数值Table 4 Parameter values of each module in the experiment

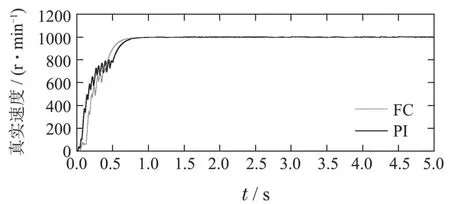
图8 在FC控制器和PI控制器下电机的真实速度Fig.8 Real speed of the motor under FC controller and PI controller

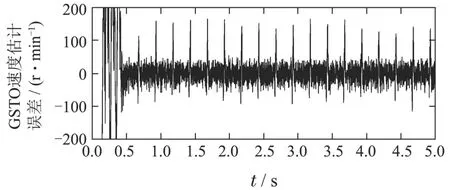
图9 GTSO对转速估计的误差Fig.9 Speed estimation error by GTSO

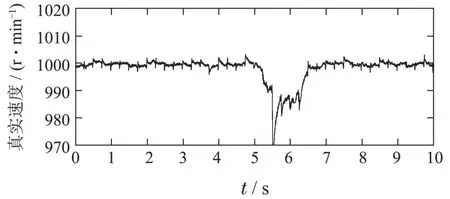
图10 在FC控制器下抗干扰性能(t=5 s时,加入负载10 N)Fig.10 Anti-interference performance under FC controller(when t=5 s,add load 10 N)

从实验结果可知,对比PI控制器,FC控制器启动阶段更快.GTSO的转速估计误差也在有界范围内,同时FC控制器具有良好的抗干扰性能,对于突加10 N的干扰负载,速度在1.4 s内收敛到设定值.

5 结论

本文提出了一种广义超螺旋观测器,估计出定子电流和反电动势,从而计算出电机转子位置和转速.仿真和实验结果均表明,与传统的滑模观测器,广义超螺旋观测器估计的电机转子位置更加精确,并且大大减小了转速估计误差,实现了对永磁同步电机的位置和速度的较高精度的估计.本文所设计的有限时间速度控制器,在上述广义超螺旋无速度传感器基础下,亦有很好的动态性能和良好的抗干扰能力.结合两者,本文既提高了无速度传感器的观测精度,又减小了速度调节的收敛时间.