基于学生成绩残差分解技术的教师教学质量评价 ＊

雷万鹏 马红梅 黄华明

（1. 华中师范大学 教育学院/湖北省基础教育研究中心，武汉 430079；2. 韶关学院 教育学部，韶关 512005）

一、研究问题和相关文献

教学质量高的教师具有巨大的经济价值（Chetty，Friedman and Rockoff，2014；Hanushek，2011），优秀师资分布不均会引起教育不公平等问题（Hanushek and Rivkin，2012；Rothstein，2010）。因此，让教师“下得去、留得住、教得好”是全球教育政策与实践领域共同关注的议题。国内关于教师劳动力市场的研究比较充分地讨论了如何让教师“下得去、留得住”的问题，但较少涉及教师是否“教得好”的问题，这可能与我国教育教学实践长期采用升学率、优秀率或班级均分等简单方式认定教师教学质量的做法有关。在教师劳动力市场改革日益深入的背景下，如何科学评价教师是否“教得好”这一问题的重要性已逐步凸显，基于学生成绩残差分解方法的教师教学质量评估有助于科学评价教师教学质量差异，对此议题的研究具有重要的理论意义和应用价值。

很多学者讨论了利用教学绩效奖励的方法激励教师提升教学质量的可能性（Cowan and Goldhaber，2018；Duflo，Dupas and Kremer，2011，2015；Pham，Nguyen and Springer，2020；Shifrer，Turley and Heard，2017；薛海平和王蓉，2016），但开展这项工作的前提是知道如何区分不同教学质量的教师，或者让教师知晓哪些指标可得到教学绩效评价体系的认可（Muñoz，Prather and Stronge，2011）。现实生活中人们往往将学生成绩与教师教学绩效进行关联，但根据学生成绩可构造出若干不同含义的指标，若用不同指标考核教师时，会引发教师采取不同的教学行为策略（Chang et al.，2020；Loyalka et al.，2019；常芳等，2018）。如我国常用班级均分和优秀率等指标评价教师教学水平，但该方法可能导致教师选择性忽视那些基础较差的学生而造成教学过程不公平问题（雷万鹏和马红梅，2019）。

1980 年代以来，学术界尝试各种方法探寻高效教师的特征，即具备哪些特征的教师能更好地促进学生成长（Hanushek and Rivkin，2012；Nagler，Piopiunik and West，2020），但至今人们尚未就“优秀教师具备哪些特征”达成共识。例如，教师受教育水平、工作经验、是否持证上岗等教师质量指标对学生成绩的影响都不稳健。出现这种情况的原因主要在于，一方面，学生学业发展过程中存在很多教师无法控制的因素，如学生素养和性情、班级风气和氛围以及学校办学环境等；另一方面，教育背景、工作年限、资格认证等教师质量指标的个体间差异不够大，从而不容易得到统计上显著的结果。有鉴于此，学生成绩残差分解的思想被引入教学评价领域，用于评估教师教学绩效或学校效能等问题（Goldhaber，Brewer and Anderson，1999）。

利用学生成绩残差鉴定教师教学质量的基本思路是，在教育生产函数分析框架下，在控制影响学生成绩的个体特征、教师资历特征、班级特征和学校特征等因素后，学生成绩预测值与班级均分的差值是由教师教学效应所致。换言之，剔除上述可观测特征对学生成绩的影响后，学生成绩的预测值与其所在班级成绩均值的残差部分是教师教学对每个学生的学业成绩产生的影响，有学者称之为“教师效能”。从学生个体层面看，若学生成绩预测值相对于班级均值的差值为正，则教师对该生的培养超出预期表现水平，属于“正增值”情形，反之亦然。从班级层面看，如果全班所有学生成绩相对于班级均值的残差之和大于零，那么这个班的任课教师可被视为“有效教师”；而残差之和为负的班级经历了“无效教学”①，后文“模型界定”部分将阐述这种教师效能评估技术的原理。

只要在班级层面对所有学生实施整群抽样，且学生相关科目的成绩可以与任课教师实现精确匹配，用学生成绩残差分解的方法评估教师教学质量就具备了现实可行性，该思路和方法也被进一步应用到学校效能评估领域。利用学生成绩残差鉴定教师教学质量的关键步骤是先获得学生成绩的预测值，而普通线性回归和多层线性分析（hierarchical linear model，HLM）都可完成这个步骤，但教育领域学者常采用更直观的HLM。如，Muñoz，Prather 和Stronge（2011）基于肯塔州杰弗逊县81 所公立学校的5700 多名在2003 年参加四年级州统考的学生，以及230 多名任课教师的信息，利用HLM 和增值评估方法对学生成绩进行预测，他们发现基于学生成绩残差分解技术得到的教师教学质量的年度相关系数均大于0.5。Subedi，Reese 和Powell（2015）基于佛罗里达州棕榈滩县薄弱高中1004 个学生及其所在班级的53 名任课教师的分析发现，学生成绩绩点方差的12%−15%可由教师的影响来解释。

需要指出的是，利用学生成绩残差分解技术评估教师教学质量的可靠性可能存在科目间差异。例如，Milanowski（2004）利用辛辛那提地区212 名公立学校教师所教3−8 年级学生的信息，综合使用增值模型和HLM 预测学生成绩，同时基于学生残差得到教师教学质量，他们以此为依据评估了俄亥俄州政府新引进的教师评价指标体系的效度②，结果显示，数学教师在两种评估方法中的相关系数高达0.43；但阅读和科学两个科目在两种方法间的一致性更低，分别为0.32 和0.27。

利用学生成绩残差分解技术分析教师教学质量的本土研究并不多见。梁文艳和杜育红（2011）基于西部地区123 所农村小学和3326 名学生在2006—2008 年的追踪信息，评估了语文和数学两个学科的教师教学质量。研究发现，农村小学教师教学质量的边际效应约为0.8 个标准差，且基于残差分解技术与利用班级均分这两种方法对教师教学质量进行排名，其重合度仅为4%−8%。本文在上述研究的基础上补充了东部和中部地区样本，也增加了中学阶段的样本，以进一步拓展该领域的研究，提供更多基于中国本土经验的证据。尽管学生成绩残差分解法被广泛地应用于教师教学绩效评价研究（Leckie and Goldstein，2015），但它也存在一定缺陷（Goldstein，2014；Goldstein and Spiegelhalter，1996）。一方面，基于学生成绩残差分解方法评估教师教学质量时对模型设定的要求较高，当影响学生学业发展的重要变量存在遗漏或这些变量的测量误差较大时，它们都将进入残差项，从而影响分析结果的精准性；另一方面，与其他教师评价指标一样，基于学生成绩残差分解技术构造的教学质量指标一旦与教师利益挂钩，教师也可能根据评价规则调整其教学行为策略。

二、研究设计

（一）数据和样本

本研究所用数据由课题组以多阶段整群抽样方法在湖北省和广东省22 区县采集而得，此项调研共收集了645 名教师和4000 多名学生的信息。班级是最后阶段的抽样单位，最基本的抽样元素包括2233 名小学5 年级学生和1965 名初中8 年级学生。被抽样班级的所有学生均参与问卷答题和纸笔测试，而班级的部分任课教师参与了教师问卷的填写。笔者根据教师在“您现在任教的主要学科”选项中的答题情况确定教师的主授科目。语文、数学和英语三科教师样本分别为181 人、153 人和159 人③，并根据学校名称和班级代码将教师数据与学生数据进行匹配④，这个匹配过程损失了大量样本，仅有237 名教师可与他们所教班级的学生匹配，各学科约三分之一被访教师进入最终分析流程。能与学生所在班级匹配的语文教师、数学教师和英语教师分别是75 人、70 人和69 人，而在所有变量上均提供了有效信息的语文教师、数学教师和英语教师人数分别是67，67 和42。

课题组对入样班级的所有学生进行了语文、数学和英语三个科目的现场测试⑤。语文成绩、数学成绩、英语成绩三个测试科目的卷面满分为100。由于参加考试的学生分别就读于小学5 年级和初中8 年级且试卷内容截然不同，原始分数不可比性。笔者先按学段将各科成绩标准化为均值为0 和标准差为1 的Z 分数，然后按照计分习惯将其二次平移为均值是70、标准差是10 的分数。语文、数学和英语三个科目最终用于分析的二次标准化成绩分别用C、M和E表示。由于存在缺失值以及师生匹配过程中的样本损失，有效样本的均值和标准差与二次标准化的分数略有区别。

（二）模型界定

公式1 所示，第c个班级的第i个学生的第j门课程成绩首先与他自己个人特征有关，学生个人特征向量（X）包括性别、所在学段、父母受教育年限和职业类别、父母是否陪读、父母工作地点变动情况及学生是否随迁外出或留守、每天的零花钱等。笔者利用不作为结果变量的其他两个科目考试成绩（Aj′，Aj″）作为学生学业基础的代理变量，以消除不随学科而变的学生个体不可观测特征，这种方法也被称之为“截面增值模型”（Hanushek，Piopiunik and Wiederhold，2019）。

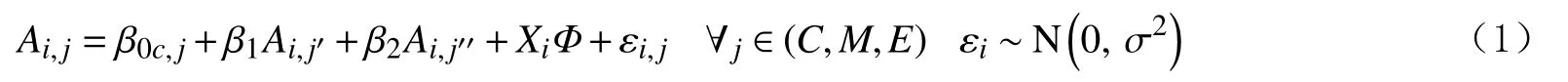
由公式1 可知，学生的成绩围绕班级均值β0c在ε范围内随机波动。剔除学生个体特征（X）和其他科目成绩（Aj'和Aj''）的影响后，班级成绩的条件均值β0c是学生个人成绩的最佳期望值，而班级成绩的条件均值是任课教师资历特征（T）和学校特征（S）共同作用的结果。如公式2 所示，在控制教师受教育年限、工作经验、职称等级（未评级、初级、中级、高级）、身份类型（公办教师、特岗教师、代课教师或其他途径）、学校区位（农村、乡镇或城区）及其聘用新教师的最低学历标准等因素的影响后，班级平均成绩围绕总体均值γ00上下波动，波动幅度是班级层面的误差项u0c。

三、主要结果与讨论

HLM 通常始于不加入任何解释变量的零模型，即单因素方差分析。零模型将被解释变量的总方差分解为组间方差（第二层方差u0c2）与组内方差（第一层方差ε2）。表1 第I 组结果显示，由零模型得到的ICC 值介于0.34−0.57 间，班级层面的成绩方差占比约为34%−57%，符合两水平HLM 建模要求。由于有效分析样本中不存在一名教师教授多个班级的情况，班级层面的方差也可被视为教师层面的方差。因此，上述结果也体现了教师对学生成绩的重要作用。

将所有控制变量均带入公式3 得到表1 第Ⅱ组结果。第（4）−（6）列结果显示，剔除若干控制变量的影响后，语文教师和数学教师的教学质量差异显著，分别占学生成绩总差异的14%和21%，相对而言，英语教师教学质量导致的学生成绩差异比例相对较小（为7%）。如前所述，ICC/（1−ICC）刻画了教师教学对全班学生成绩的整体影响，表1 第（4）−（6）列的辅助统计量ICC/（1−ICC）表明，其他条件都相同的两个班级由教师教学质量差异所致的学业成绩差异介于0.07−0.27 个标准差间。其中，学生的数学成绩受教师教学质量影响最大，“教得好”的数学教师可将全班学生数学成绩整体提升0.27 个标准差；而英语教师教学质量对学生成绩差异的影响最小，教学质量高的英语教师仅能将全班学生成绩整体提升0.07 个标准差。上述结果与Goldhaber，Brewer 和Anderson（1999）利用美国教育追踪调查数据（National Educational Longitudinal Study，1988）的分析结果大致相同。究其原因可能是，学生在数学科目上的可塑性更强，只要教师教会了学生基本思维方法并举一反三地练习，提高数学成绩相对容易，但语文和英语等语言学科需要长期积累，教师在短期内提高学生成绩的难度较大（Chetty，Friedman and Rockoff，2014；雷万鹏和马红梅，2019）⑥。上述研究结果的启示是，数学教师可更充分地利用相互观摩和合作的方式提高教学技能与质量，从而更高效地促进学生数学成绩的提升。

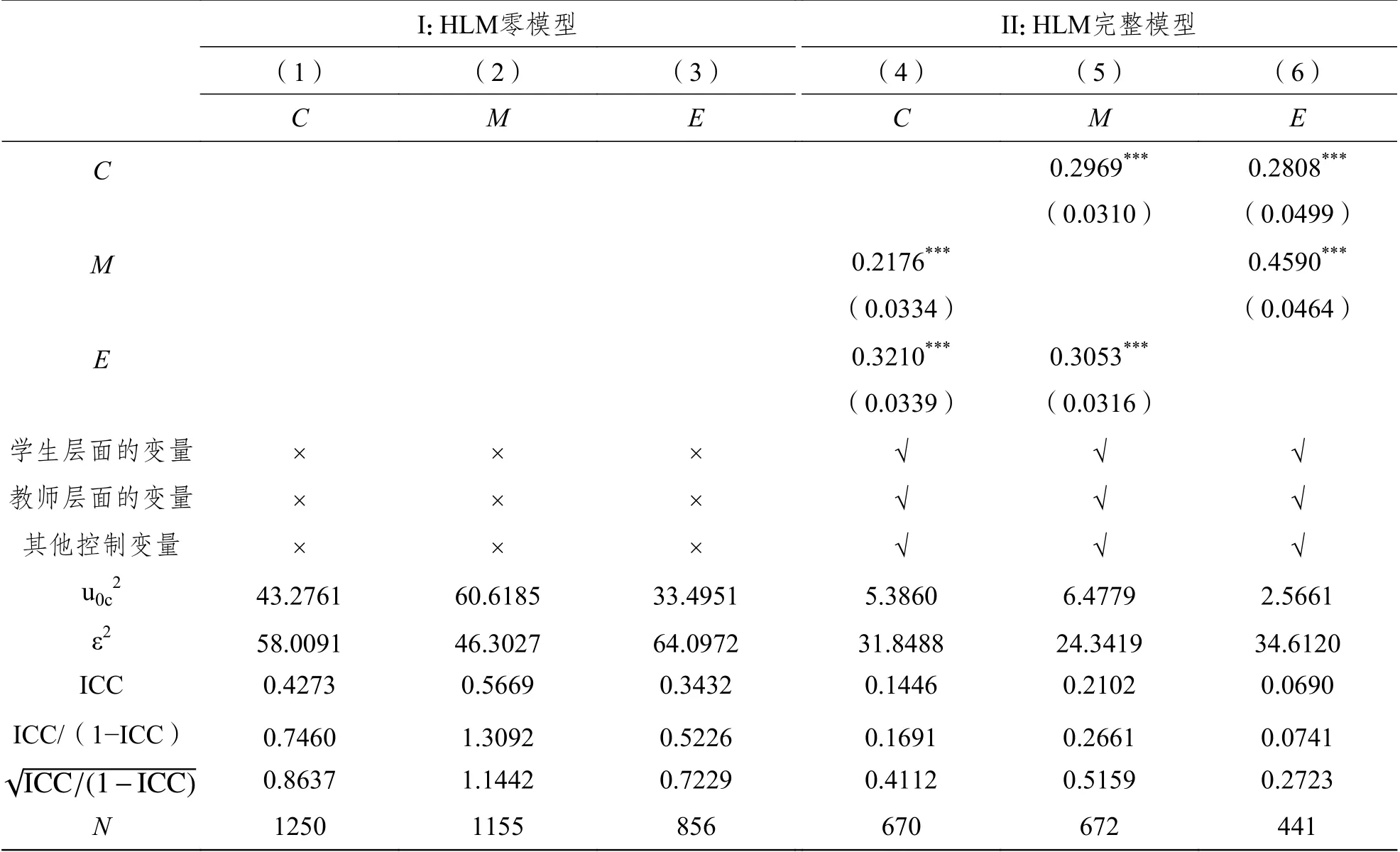
表1 基于HLM 的学生成绩方差分解

笔者结合表1 中的教师教学边际效应量做了推算。如果将教学质量最差的教师替换为平均水平的教师，语文、数学和英语成绩最低的班级均分将分别提高4.7 分、4.5 分和6.9 分，约相当于0.5−0.7 个标准差。而如果让一名教学质量处于平均水平的教师教成绩最好的班级，全班学生的语文、数学和英语三科成绩将分别降低3.3 分、10.5 分和9.2 分；换言之，成绩最好的班级若被安排给教学质量处于平均水平的教师任教，全班学生的三科成绩将集体下滑0.3−1 个标准差。这与Borman 和Kimball（2005）得到的教师教学质量效应量置换分析结果大致相同⑦。笔者根据表1 第（4）−（6）列结果简要描述教师教学质量的分布特征，得到以下两个结论。

第一，如表2 第三行结果所示，三个科目中均有近50%学生的预期成绩低于班级均值，但数学教师可使56.9%的学生的预期成绩超过班级均值。而且，由于成绩预期值低于班级均值的那部分学生的负残差和总体上大于成绩预期值高于班级均值的那部分学生的正残差之和，因此，语文教师、数学教师和英语教师对学生个人层面的学业增值贡献均值均为负，分别是−0.346、−0.026 和−1.097，且标准差均大于5。这表明，同样的教学质量对不同学生的学业增值影响差异较大。

第二，如表2 最后一行结果显示，经过收缩因子调整的班级层面成绩残差值之和为正的语文、数学和英语教师比例分别是38.5%、53.8%和44.6%。换言之，语文和英语科目的教师实现有效教学的难度更大，而超过一半的数学教师均做到了有效教学。这也可以从表2 倒数第二行的结果得到证实，数学教师对整个班级的平均影响是0.023 个标准差，但语文和英语科目的教师教学质量指数均为负数。

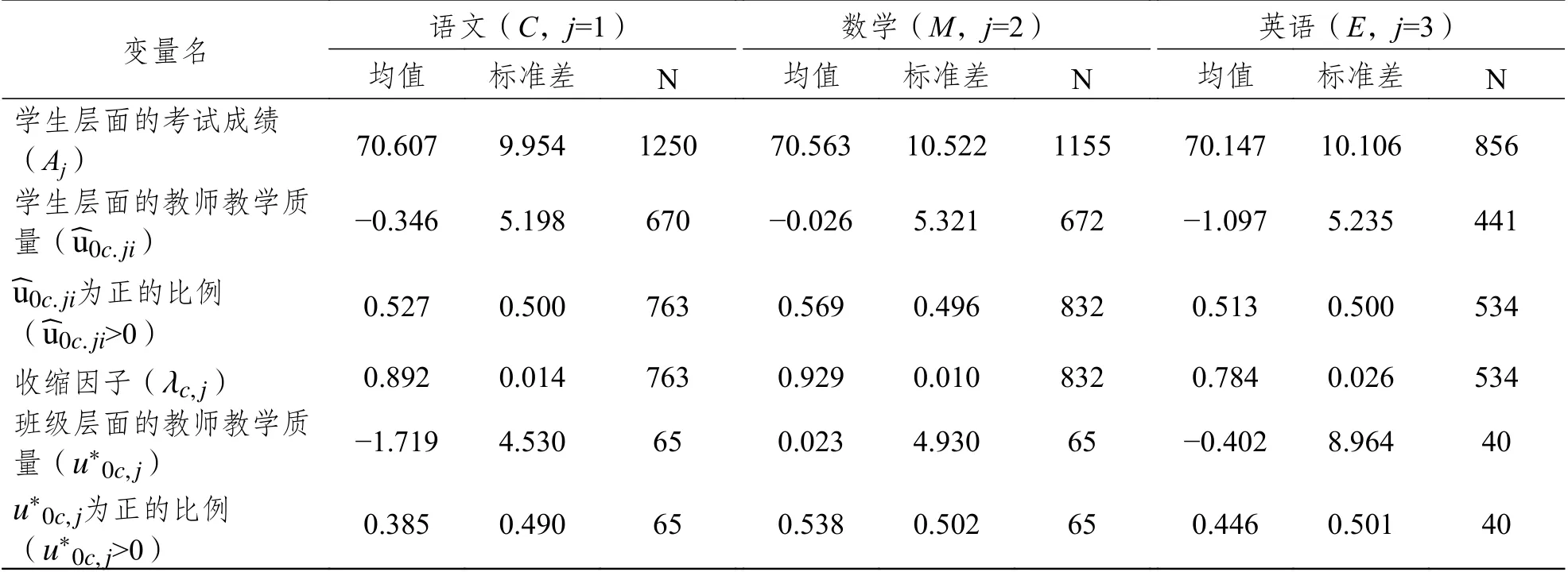
表2 教师教学质量的分布特征

四、结语

基于湖北和广东两省的调研数据，本研究利用HLM 方法预测学生成绩，通过学生成绩预测值与班级均值间的残差构造教师教学质量指标。我们将学生成绩预测值与班级均值之间的残差视为由教师教学给学生学业增值带来的净效应，以此为基础探讨语文、数学和英语三门课程任课教师的教学质量效应量及其差异。本文对识别高效优质教师和推动教师评价改革、改进教学过程公平等方面具有现实意义和应用价值。

本研究的主要结论是：第一，教师教学质量对学生学业增值影响较大，教师之间教学质量差异也较大。在控制了学生背景特征、教师资历特征和学校特征等因素后，教师的教学质量每相差一个单位，学生成绩分别变动0.3−0.5 个标准差。其中，数学教师教学质量的边际效应量最大，约0.5 个标准差；而英语教师和语文教师的边际效应分别为0.3 个标准差和0.4 个标准差。若教学质量最低的教师均能达到平均水平，全班学生三科成绩可提高0.5−0.7 个标准差；若将教学质量最好的教师替换为平均水平的教师，全班成绩将整体下滑0.3−1 个标准差。第二，同一教师对不同学生的学业发展的贡献差异较大。由于成绩预期值低于班级均值的学生的负残差和整体上多于成绩预期值高于班级均值的学生的正残差和，教师教学质量的均值较低且变异系数大。

本文有两个尚待改进之处：一是科学地评价教师教学质量有赖于扎实的基础数据建设工作作为支撑，今后可利用追踪调查的方式建设多期数据，基于多期数据的增值评估方法可提高研究结果的精确性。二是利用学生成绩残差分解技术评估教师教学质量的方法的便捷性和可操作性不足，一线教育教学工作者较难掌握，未来还需要探索更简洁实用的方法，以更好地服务于教师绩效评价实践工作。

（黄华明为本文通讯作者）