内齿圈裂纹扩展对复合两级行星轮系均载特性的影响研究

李国彦， 沈 奇， 牛蔺楷， 马 亮， 董德浩

(1. 太原理工大学 新型传感器与智能控制教育部与山西省重点实验室，太原 030024；2. 电子科技大学 机械与电气工程学院，成都 611731； 3. 上海航天设备制造总厂，上海 201100)

复合行星轮系是指包含一个或多个：双排行星轮系(一个行星轮组中有两个行星轮相互啮合)、阶梯式行星轮系(一个行星轮组中有两个行星轮通过共同的行星轮轴联结)、多级行星轮系的齿轮传动系统[1-2]，是风电机组、直升机、工程机械等复杂设备的核心传动部件。工作中齿面承受着交变载荷的作用，容易产生损伤，从而降低系统的传动精度、效率及平稳性，开展损伤复合行星轮系动力学研究可为其故障诊断及可靠性分析提供必要的理论依据[3]。

行星轮系的均载特性对齿轮箱的运行性能及服役寿命有重要的影响，近年来受到国内外研究者的广泛关注。Park等[4]研究了不同支撑方式对风机变桨减速机行星轮系均载特性的影响；Kim等[5]研究了行星轮轴孔误差对行星轮系均载行为的影响；Iglesias等[6]指出浮动太阳轮结构能极大的改善行星轮系的均载行为；Li等[7]指出行星轮间的不均载会严重降低直升机行星轮系的运行可靠性；Qiu等[8]研究了重力、齿圈支撑刚度及台板倾角对风机行星轮系均载性能的影响；魏静等[9]分析了误差、柔性销轴及工况参数对人字齿行星轮系均载性能的影响；巫世晶等[10-11]研究了啮合误差、安装误差位置及其相位角对Ravigneaux式复合行星轮系均载特性的影响；张霖霖等[12-13]分析了啮合相位、偏心误差、基本构件浮动、柔性内齿圈等对人字齿行星轮系静态均载特性的影响；谭援强等[14]开展了封闭差动行星轮系均载性能试验研究，探索了浮动太阳轮、柔性销轴、柔性内齿圈等均载措施对其均载性能的影响。以上文献从齿轮误差、齿侧间隙、啮合刚度及啮合相位、支撑方式、基本构件浮动量、柔性销轴以及工况参数等方面对行星轮系的均载性能进行了研究，但这些研究只针对完好的行星轮系，损伤行星轮系的均载特性退化规律需进一步深入研究。

复合行星轮系内部结构复杂，非线性因素丰富，其动力学建模具有复杂性。已有的模型中，关键模型参数被简化，主要体现在：啮合刚度被简化为常数、平均啮合刚度与变刚度的叠加函数、接触线长度的一次函数、矩形波、梯形波等；很少准确计入各啮合副间的啮合相位关系；支撑刚度被忽略或简化为常数；此外，缺乏损伤复合行星轮系的建模与分析。因此，已有的模型不能准确地反映复合行星轮系的振动机理，无法用于损伤复合行星轮系的动力学行为研究。

齿根疲劳裂纹是导致行星轮系性能退化的主要损伤模式之一。裂纹扩展会使系统内部产生复杂的非线性动力学行为。本文通过构建计入齿根裂纹损伤的复合行星轮系动力学模型，研究裂纹扩展对系统均载性能的影响。首先，建立裂纹齿圈时变啮合刚度模型，研究不同裂纹程度与时变啮合刚度之间的量化关系，将损伤以内部激励的形式引入到复合行星轮系动力学模型中；其次，推导滚动体与滚道之间的非线性弹性接触力，得到各构件的时变支撑刚度；进一步，获取不同裂纹扩展程度下各啮合副的啮合振动信号，综合采用时间历程、频谱、相轨迹及Poincaré映射图分析裂纹扩展对系统非线性振动特性的影响；最后，计算各啮合副均载系数，分析裂纹扩展对系统均载特性的影响规律。

1 计入齿根裂纹损伤的复合行星轮系动力学建模

1.1 复合行星轮系传动原理

图 1为复合行星轮系传动简图。

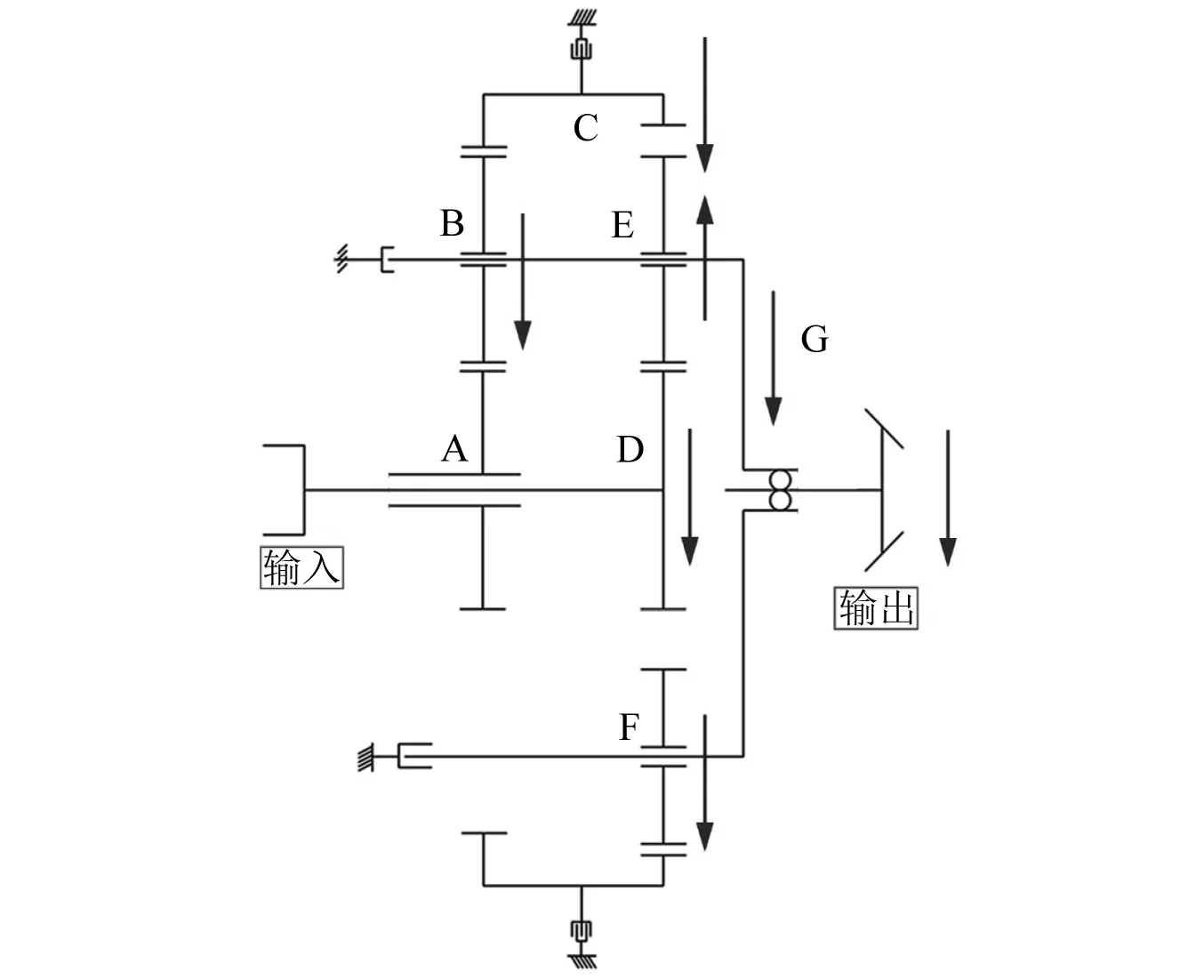
A.第一级太阳轮；B.第一级行星轮；C.齿圈；D.第二级太阳轮；E—F.第二级行星轮-行星轮啮合副；G.行星架。

第一级是简单行星轮系，由太阳轮、齿圈和三个行星轮组成；第二级是双排行星轮系，由太阳轮、齿圈和三个行星轮—行星轮啮合副组成；两级通过共同的行星架耦合在一起；两级的齿圈被制造为一个整体。行星轮系处于前进一档时传动比为2.08，设定输入转速为700 r/min，负载转矩为200 N·m，其余基本参数如表 1所示。

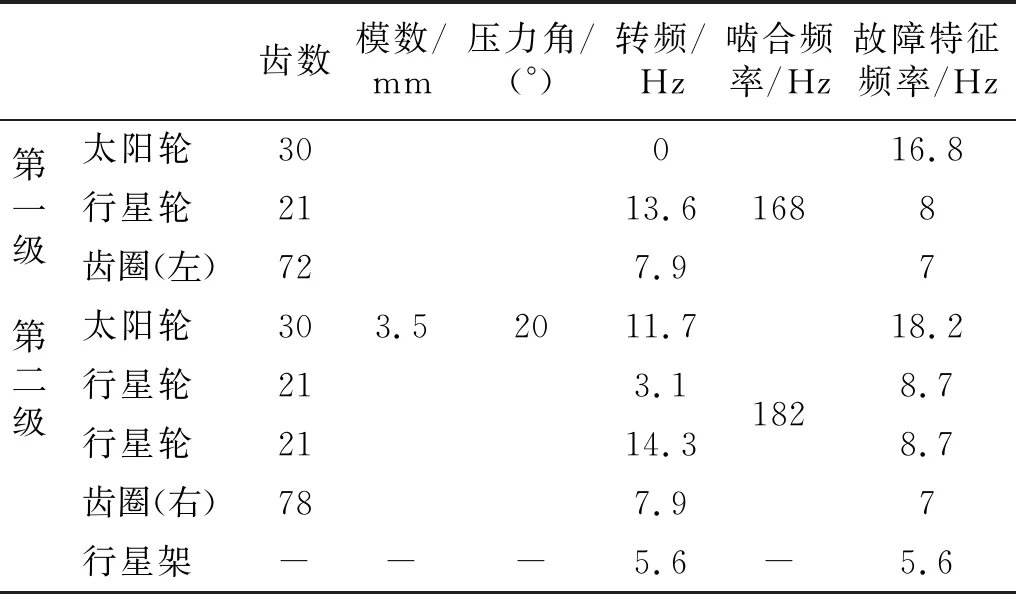
表1 复合行星轮系基本参数

1.2 计入齿根裂纹及啮合相位的时变啮合刚度

本小节基于悬臂梁理论及能量法建立含裂纹齿圈时变啮合刚度模型。

图 2为含裂纹齿圈及其横截面。假设裂纹产生于齿圈齿根处，沿与轮齿中心线呈v=45°的方向扩展，裂纹尺寸用q1表示，当裂纹扩展到与轮齿中心线相交时，定义裂纹程度为50%(对应的裂纹长度为6.41 mm)，之后裂纹改变扩展方向，沿与轮齿中心线呈v=-45°的方向扩展，裂纹尺寸用q2表示，直到轮齿瞬间断裂为止。由图可知，完好轮齿的横截面为矩形A-B-C-D，当轮齿进入损伤区域啮合时，轮齿的横截面相对于正常情况产生了改变，导致轮齿刚度值变化。

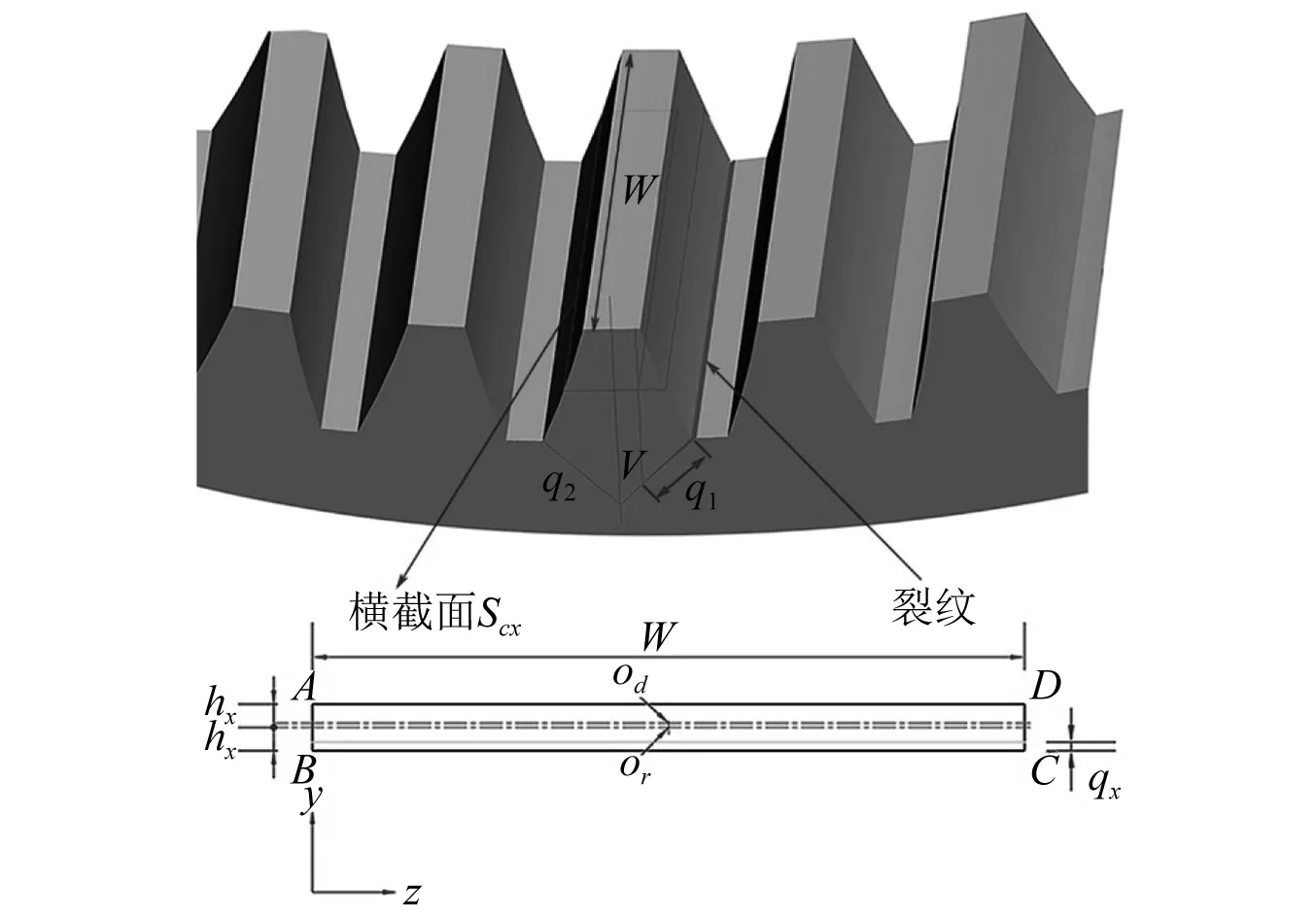
图2 含裂纹齿圈及其横截面

图 3为含裂纹齿圈轮齿悬臂梁模型。F是沿啮合线方向的法向啮合力；α1是啮合点对应的啮合角；α2是基圆圆弧对应的圆心半角；α3是近似齿根圆弧对应的圆心半角；αf为齿根圆压力角；d为啮合点到齿根处的距离；x为啮合点到齿根的区域内任意一点到齿根圆的距离；dd为受力边界线的长度；h为啮合点到轮齿中心线的距离；hx是啮合点到齿根的区域内任意一点到轮齿中心线的距离；hd为受力边界点到轮齿中心线的距离；rb和rf分别是基圆和齿根圆半径。

图3 含裂纹齿圈轮齿悬臂梁模型

根据能量法，轮齿单齿综合啮合刚度由弯曲刚度kb、剪切刚度ks、轴向压缩刚度ka及赫兹接触刚度kh组成，各刚度分量与轮齿横截面的惯性矩Ix、面积Ax、接触宽度w有关，微分方程分别为：

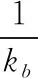
(1)

(2)

(3)

(4)

式中:E、G和υ分别为杨氏模量、剪切模量和泊松比。根据悬臂梁模型及渐开线特性，h、d和x的表达式分别为：

h=rb[(α2-α1)cosα1+sinα1]

(5)

d=rfcosα3-rb[cosα1-(α2-α1)sinα1]

(6)

x=rfcosα3-rb[cosα-(α2-α)sinα]

(7)

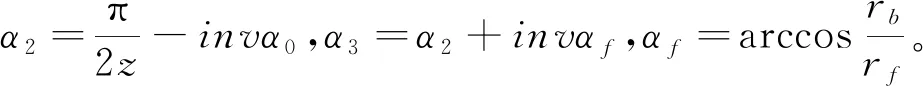
正常轮齿横截面的惯性矩Ix和面积Ax为：

(8)

Ax=2hxw=

2rb[(α2-α)cosα+sinα]w, 0≤x≤d

(9)

其中:hx=rb[(α2-α)cosα+sinα]

当裂纹未扩展到中心线时，轮齿横截面的惯性矩和面积分别为：

(10)

Ax=(hx+hd)w=

(11)

式中：hd=rfsinα3-q1sinv；受力边界线的长度dd的表达式为：

dd=rfcosα3-rbcosαd-rb(αd-α2)sinαd

(12)

式中，αd可由下式求解所得：

rb(αd-α2)cosαd=rbsinαd-rfsinα3+q1sinv

(13)

当裂纹扩展至中心线后，扩展路径改变，轮齿横截面的惯性矩和面积分别为：

(14)

Ax=(hx-hd)w=

(15)

式中，hd=q2sinv；受力边界线的长度dd的表达式为：

dd=rfcosα3-rbcosαd-rb(αd-α2)sinαd

(16)

式中，αd可由下式求解所得：

rb(αd-α2)cosαd=rbsinαd-q2sinv

(17)

一个啮合周期内存在单齿和双齿啮合区。单齿综合啮合刚度表示为：

(18)

多齿综合啮合刚度表示为：

(19)

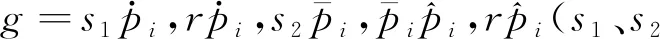
计入啮合相位差的时变啮合刚度为：

kg(t)=kg(t-γtmn)

(20)

式中：tmn是第n级齿轮系的啮合周期，γ是各啮合副的啮合相位[15-16]。图 4为计入啮合相位的各啮合副时变啮合刚度。

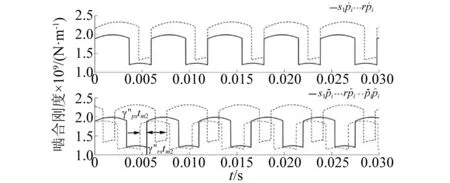
图4 计入啮合相位的时变啮合刚度

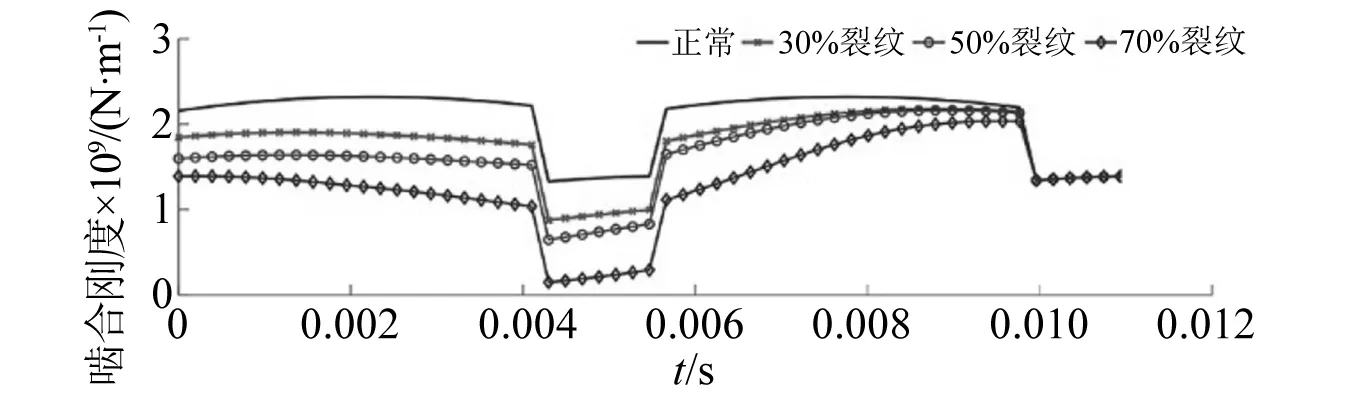
图5 不同裂纹程度下齿圈-行星轮啮合副的时变啮合刚度

图6 30%裂纹损伤情况下各齿圈-行星轮啮合副的时变啮合刚度

1.3 时变支撑刚度

由于实际承受外部载荷的滚动体数量会随保持架的旋转而变化，因此，支撑刚度为周期性时变的。以行星轮轴承为例(图 7)，第i个滚动体与滚道之间的接触变形δi是外圈水平位移xj、竖直位移yj、第i个滚动体的角位置θi，以及径向游隙γ0的函数。根据几何位置关系推导可知：

图7 行星轮滚针轴承模型

δi=xjcosθi+yjsinθi-γ0

(21)

式中：θi=2π(i-1)/z+wct(i=1,2,…,z)，z为滚动体个数，保持架的角速度为wc：

(22)

式中:d为滚子直径，D为轴承节径，wi为内圈转速，wo为外圈转速；初始位置角取0。

根据非线性赫兹接触理论可得滚动体与滚道之间的非线性弹性接触力：

(23)

(24)

轴承基本参数如表 2所列。图 8 展示了太阳轮、行星架及行星轮的时变支撑刚度曲线。

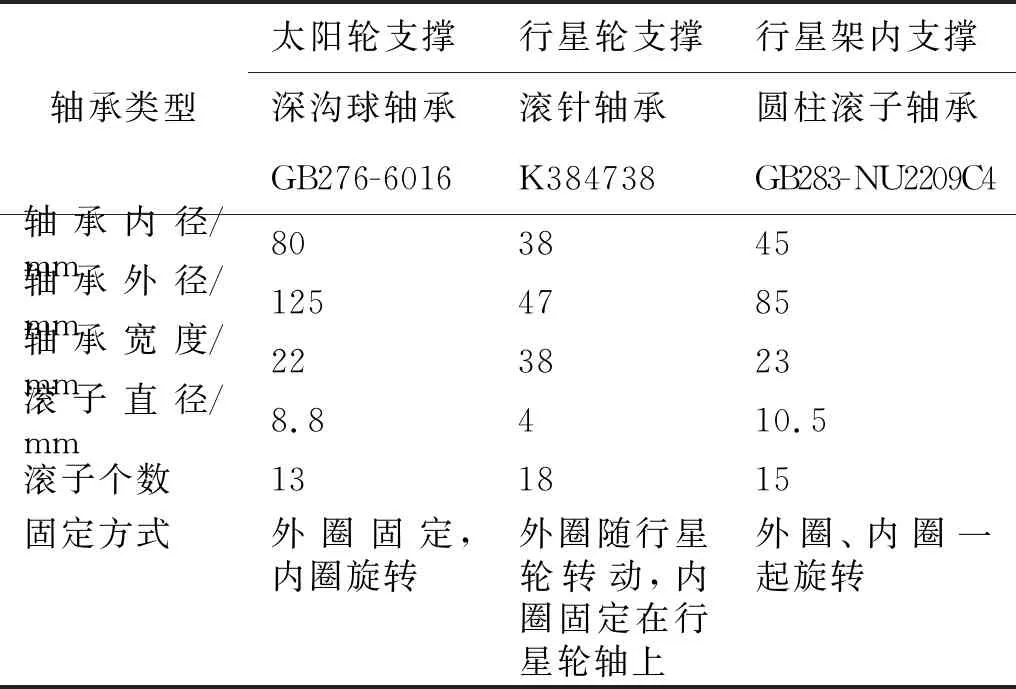
表2 复合行星轮系轴承参数

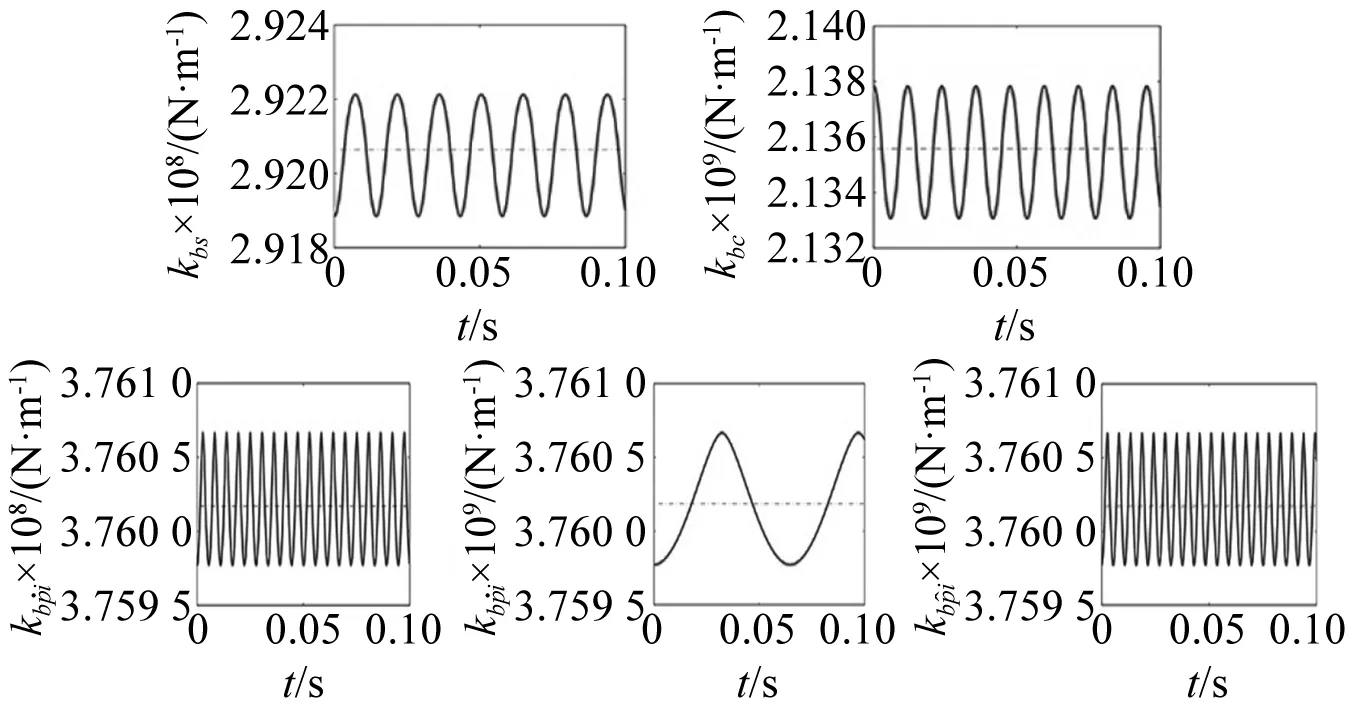
图8 各轴承时变支撑刚度

1.4 计入齿根裂纹的复合行星轮系非线性动力学模型

图 9 为复合行星轮系动力学模型，考虑了计入啮合相位的时变啮合刚度、时变支撑刚度、阻尼等非线性因素。详细的动力学微分方程推导在文献[15-16]中给出。通过建立裂纹参数与时变啮合刚度之间的量化关系，可将损伤以内部激励的形式引入到动力学建模中，从而建立计入齿根裂纹损伤的复合行星轮系动力学模型。

图9 复合行星轮系动力学模型[15-16]

2 复合行星轮系均载系数定义

2.1 动态啮合力

啮合力由弹性恢复力和阻尼力组成，大小取决于各啮合副相对位移、啮合刚度和阻尼，定义为[15-16]:

(25)

其中，各啮合副沿啮合线方向的相对位移δg为：

(26)

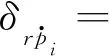
(27)

(28)

(29)

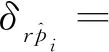
(30)

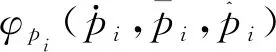
2.2 均载系数

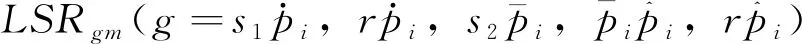
式中：m代表啮合周期；N1是第一级齿轮系的行星轮数；N2是第二级齿轮系的行星轮数。

定义LSRg为每一循环周期各啮合副的均载系数，即一个循环周期内，取各啮合副的每一齿频周期均载系数的最大值作为啮合副g的均载系数：

LSRg=max{|LSRgm-1|+1},m=1, 2， 3，…

(32)

定义复合行星轮系的均载系数LSR为：

LSR=max{LSRg}

(33)

3 裂纹扩展对复合行星轮系均载性能的影响

本小节以第二级齿圈齿根裂纹为例，研究裂纹扩展对复合行星轮系均载性能的影响，假设裂纹沿1.2小节描述的扩展路径，间隔为10%扩展，损伤程度达到70%时，轮齿瞬间断裂。

3.1 裂纹扩展对齿圈-行星轮啮合振动特性的影响

运用四阶Runge-Kutta法求解系统动力学微分方程，得到各构件的振动响应，进一步得到各啮合副沿啮合线方向的相对位移。图 10为正常情况下各啮合副沿啮合线方向的相对位移。由于啮合过程中存在单双齿交替啮合现象，因此啮合振动具有时变性及周期性；太阳轮-行星轮啮合副的平均啮合振动为0.40 μm，齿圈-行星轮啮合副的平均啮合振动为0.32 μm，行星轮-行星轮啮合副的平均啮合振动为0.43 μm。

图10 正常情况下各啮合副的啮合振动

图11 不同裂纹程度下第二级齿圈-行星轮啮合副的啮合振动

图12 正常情况第二级齿圈-行星轮啮合副啮合振动

图13 30%裂纹第二级齿圈-行星轮啮合副啮合振动

图14 50%裂纹第二级齿圈-行星轮啮合副啮合振动

随着中心构件的旋转，裂纹轮齿以tr为间隔进入啮合，引起周期性冲击，对正常的啮合振动进行调制，在啮合谐波周围形成以齿圈故障特征频率fr为间隔的边频带。但早期裂纹(30%以内)引起的冲击振动能量较小，边带谱线的幅值非常微弱，几乎提取不到；随着裂纹扩展，啮合副沿啮合线方向的冲击振动明显增大，边带谱线的幅值逐渐增大，相轨迹中与冲击振动对应的边缘曲线向外扩散，Poincaré映射图中点集离散程度增大。以上特征可以指示裂纹的产生及对其演化程度进行有效跟踪。

3.2 裂纹扩展对齿圈-行星轮啮合副均载特性的影响

通过式(31)～(33)求得不同裂纹损伤程度下各啮合副及系统均载系数。图 15为第二级三对齿圈-行星轮啮合副之间载荷分配随裂纹损伤程度变化的直方图。可以看出，随着中心构件旋转，裂纹轮齿周期性进入啮合，对应的啮合副啮合刚度降低，啮合振动增大，三对啮合副之间载荷分配出现不平衡，产生偏载现象；随着裂纹扩展，偏载程度越来越严重，50%裂纹损伤情况下，含裂纹啮合副仅承担26%的载荷，另外两对啮合副分别承担37%的载荷。

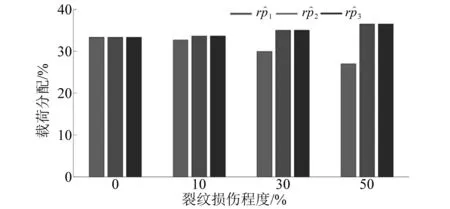
图15 第二级齿圈-行星轮啮合副之间载荷分配随裂纹损伤程度变化

图16 30%裂纹情况下第二级齿圈-行星轮啮合副各齿频周期内的均载系数

图 17为系统均载系数随裂纹扩展的变化曲线，裂纹从10%等间隔扩展到70%，对应的系统均载系数分别为1.03，1.06，1.10，1.15，1.19，1.26，1.61，非线性地增长了61%；裂纹后期，系统均载系数急剧增大，各啮合副间载荷分配严重不平衡，从而引起部分构件过载、转动不平稳、振动噪声增大甚至齿轮失效等问题。

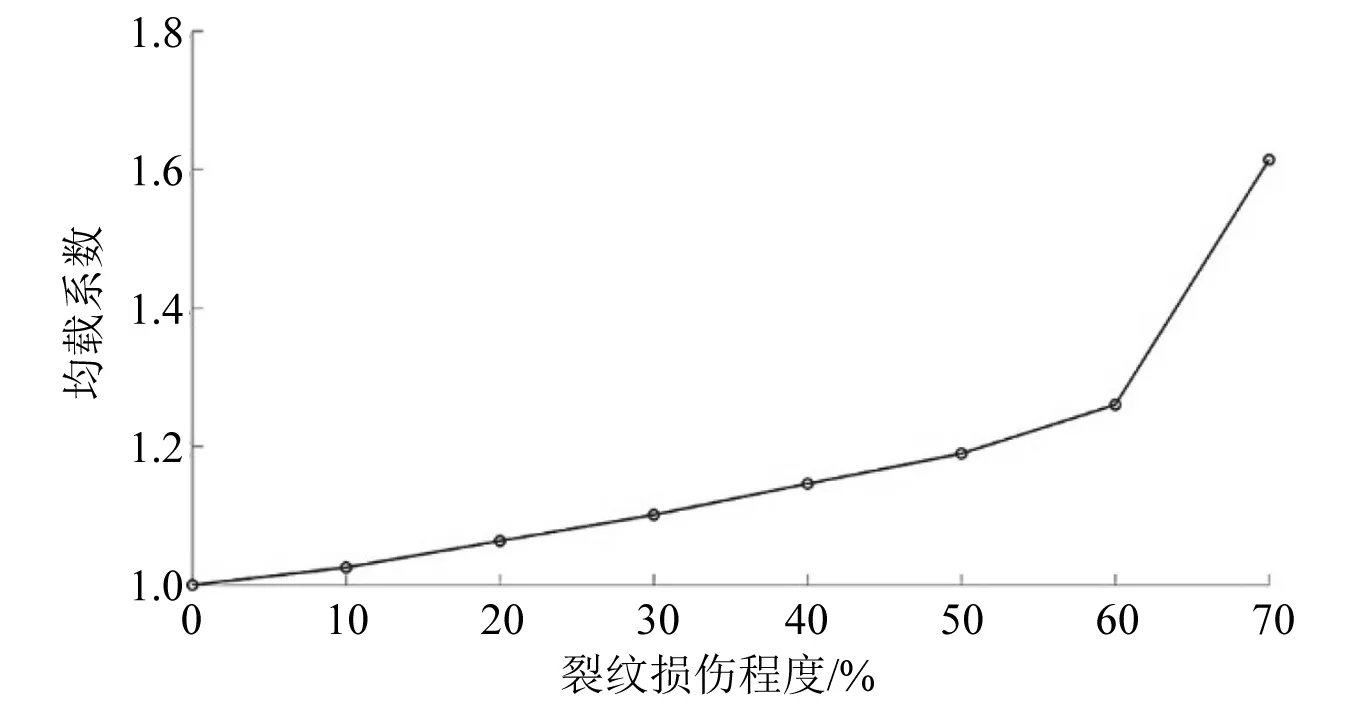
图17 系统均载系数随裂纹扩展的变化曲线

4 结 论

(1)建立了计入齿根裂纹损伤的复合行星轮系非线性动力学模型，考虑了时变啮合刚度、啮合相位、裂纹及时变支撑刚度，该损伤模型可用来仿真复合行星轮系的故障响应信号。

(2)通过数值分析得到不同裂纹扩展程度下各啮合副的啮合振动信号，综合采用时间历程、频谱、相轨迹及Poincaré映射图分析裂纹扩展对啮合振动特性的影响；结果表明：裂纹的产生会在时域中引起周期性冲击序列，在频谱中形成等间隔的边带谱线；随着裂纹扩展，冲击序列的幅值明显增大，边带谱线的幅值逐渐增大，相轨迹中与冲击振动对应的边缘曲线向外扩散，Poincaré映射图中点集离散程度增大。以上特征可以指示裂纹的产生并对其演化程度进行有效跟踪。

(3)通过计算各啮合副均载系数，分析裂纹扩展对系统均载特性的影响规律；研究表明：裂纹的产生及扩展对系统均载特性有显著的影响；损伤啮合副啮合刚度的降低及啮合振动的增大导致各啮合副间载荷分配不平衡，产生严重的偏载；由于裂纹轮齿周期性进入啮合，各啮合副的均载系数产生周期性波动；随裂纹扩展，复合行星轮系的均载系数呈非线性增长趋势，从而影响齿轮箱的运行性能及服役寿命。

上述研究可为复合行星轮系均载特性分析及故障诊断提供相关参考。