桥梁收缩徐变诱发高速列车-CRTS Ⅱ型板式轨道-桥梁系统非线性动力相互作用研究
2021-06-30陈兆玮
陈兆玮
(重庆交通大学 机电与车辆工程学院,重庆 400074)
混凝土桥梁的收缩徐变效应在高速铁路桥梁工程中不可避免,其会引起桥梁的竖向变形,并进一步引起铺设在桥面上的轨道结构发生变形[1]。这种桥梁变形对普通轨道结构的影响较小。但是对于纵连板式无砟轨道(我国常用的为CRTS II型纵连板式轨道)来说,由于纵向连接特性,其对基础变形的抵抗能力及适应能力较差。一旦桥梁发生竖向变形,梁端会产生折角等不连续变形,进而必然导致连续的纵连板式轨道变形及不连续的桥梁变形之间出现局部脱空现象[2]。这些局部脱空会改变轨道结构刚度、增大轨道结构附加应力,对轨道的稳定性产生恶劣影响。当高速列车通过时,这些脱空区域处底座和桥面会出现非线性动态接触行为,影响轨道结构的力学性能及轮轨非线性接触特性,严重时还可能导致轨道混凝土结构被拉裂、严重威胁高速列车的运行安全。
目前国内外已有一些学者开展了收缩徐变对车轨桥系统影响的研究,其研究方法多为建立车轨桥系统的有限元模型或推导系统振动方程并进行数值求解。徐庆元等[3]基于车辆-轨道耦合动力学理论,建立了列车-CRTS Ⅱ型板式轨道-轨桥系统的有限元模型,研究了徐变对系统内各部件振动特性的影响规律。为了研究徐变上拱对于轨道-桥梁系统相互作用的影响,颜轶航等[4]建立了三跨连续梁桥及简支梁桥的轨道-桥梁系统有限元模型,分析了徐变对桥上轨道钢轨附加应力、扣件力以及列车走行性的影响。针对32 m简支箱梁桥,方辉等[5]建立了列车-轨道-桥梁耦合动力学模型,研究了列车通过时的系统振动。周爽等[6]针对高速列车运营阶段简支箱梁桥准静态变形对轨道平顺性的影响而引起的行车安全性问题进行了分析研究。基于列车-轨道-桥梁动力相互作用理论,Chen等[7]建立了考虑收缩徐变的车轨桥动力学模型,研究了收缩徐变所导致的混凝土结构变形,并在此基础上探讨了列车通过时的动态特性。王昆鹏等[8]基于刚柔耦合动力学理论,建立了柔性车桥动力学模型,研究了徐变对系统的影响。杨宏印等[9]推导了轨道不平顺的移动车轮-轨道-桥梁耦合单元方程,采用数值求解算法研究了车轨桥系统收缩徐变的影响。既有研究提出了很多重要的结论,但是鲜有针对纵连板式轨道的研究,特别是纵连板式轨道底座与桥面之间的非线性动态接触,而该问题则是研究桥梁收缩徐变下高速列车-纵连板式轨道-桥梁系统非线性动力相互作用的重要前提。
针对高速铁路混凝土桥梁收缩徐变这一实际工程问题,本文深入研究其引起的高速列车-纵连板式轨道-桥梁系统非线性动力相互作用问题。首先对桥梁收缩徐变下纵连板式轨道-桥梁系统非线性接触行为产生机制进行讨论,然后提出桥梁收缩徐变条件下高速列车-纵连板式轨道-桥梁系统非线性动力相互作用研究方法,在此基础上研究桥梁收缩徐变对桥轨非线性接触、轨道层间相互作用以及列车动态特性的影响,并在最后一部分对本文工作进行了总结。
1 桥梁收缩徐变条件下纵连板式轨道-桥梁系统非线性接触行为产生机制
纵连板式轨道主要包括钢轨、扣件、轨道板、CA砂浆、底座板以及滑动层(两布一膜)构成,如图1所示。与其他无砟轨道相比,该结构最大的特点是:①结构沿纵向为一连续整体;②底座板与桥面未浇筑为一体,相互之间通过一层很薄的滑动层进行隔离,因此轨道和桥面之间可以发生相对滑动、脱空等行为。
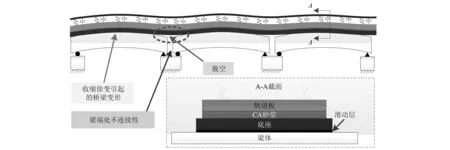
图1 桥梁收缩徐变条件下纵连板式轨道-桥梁系统非线性接触
当混凝土桥梁发生收缩徐变后会出现竖向变形,进而引起铺设在桥面上的纵连板式轨道发生竖向弯曲变形。同时由于轨道结构变形的连续性以及不同桥梁变形的不连续性,梁端位置必然出现局部脱空,降低轨道结构稳定性。
当列车通过时,轮载会导致脱空区域的变化,脱空边缘位置会出现“分离-接触-再分离”的动态循环接触行为直至列车完全通过。这种非线性动态接触导致轨道结构内部产生巨大的附加应力,恶化轮轨非线性接触关系,威胁高速列车的正常运行。因此需要深入研究这种动态接触的变化以及其对车轨桥系统的影响。
2 桥梁收缩徐变条件下高速列车-纵连板式轨道-桥梁系统非线性动力相互作用研究方法
桥梁收缩徐变引起纵连板式轨道与桥面之间出现非线性动态接触行为,进而影响整个系统的力学特性。针对该问题,本文形成了桥梁收缩徐变条件下高速列车-纵连板式轨道-桥梁系统非线性动力相互作用研究方法,如图2所示。
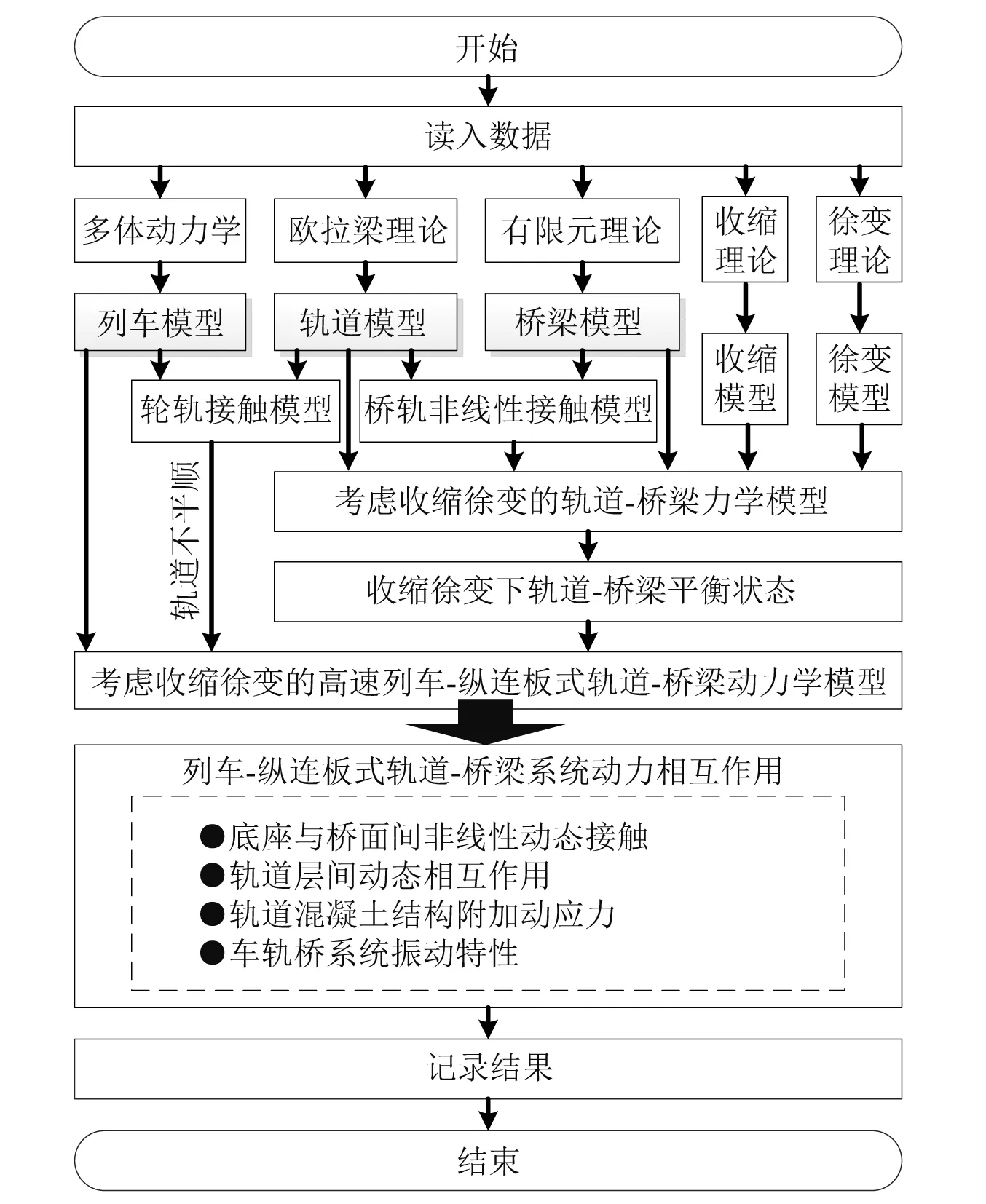
图2 收缩徐变下车轨桥系统非线性动力相互作用研究方法
从该技术路线图中可以清晰看出,有三个研究内容值得着重介绍,分别是:混凝土收缩徐变模型的建立、桥轨非线性接触模型的建立以及高速车轨桥动力相互作用模型的建立,下面将分别进行阐述。
2.1 混凝土收缩徐变模型
目前对于收缩徐变模型已有很多研究[10-12],学者采用较多的模型,ACI模型、CEB-FIP模型、B3模型等。为了能更准确模拟我国混凝土的收缩徐变特性,本文采用了《公路钢筋混凝土及预应力混凝土桥涵设计规范(JTG D62—2012)》中规定的模型(简称JTG2012模型)。
JTG2012徐变模型可以表示为
(1)
式中:φ(t,ts)为从时刻ts到时刻t的徐变系数;ts为混凝土开始发生徐变时的龄期;φ0为名义徐变系数。
在本文中,徐变效应考虑为作用在桥梁上的外加载荷,徐变虚拟力表示为
(2)
式中:ε(ts)为时间ts时的应变;E为弹性模量。
因此,从ts时刻到t时刻的徐变应变表示为
(3)
假设每一个计算步内的结构应力不变,式(3)可以进一步简化为
(4)
(5)
式中:tj为混凝土施加载荷时的龄期;ai(tj)和Γi为徐变模型有关的系数。
更进一步,从ts时刻到t时刻的徐变增量为
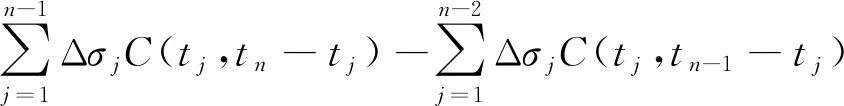
(6)
基于有限元理论,徐变应变增量Δεc,n和结构变形增量Δδn可以写为
Δδn=B-1Δεc,n
(7)
借助坐标变换和式(7)即可求得全桥的徐变变形。
JTG2012收缩模型为
(8)
式中:εcs(t,ts)为ts时刻到t时刻的收缩应变;εcso为名义收缩系数。
参照徐变的计算方法,收缩效应也假设为收缩虚拟力
Pcs=EAεcs
(9)
式中:A为桥梁截面面积;εcs为收缩应变。
从t1时刻到t2时刻的收缩应变可以表示为
εcs(t2-t1)=εcs(t2-ts)-εcs(t1-ts)
(10)
根据式(10)中的收缩应变及式(7)中的转换关系,即可确定收缩效应下的桥梁变形。
2.2 桥轨非线性接触模型
桥轨非线性接触模型采用一系列单向受压弹簧进行模拟,非线性接触弹簧刚度的表达式为
(11)
式中:ktb为接触弹簧刚度;Zba和Zb分别为某一接触弹簧位置处的底座位移和桥面位移;Esl、Asl、hsl为滑动层的弹性模量、投影面积和厚度;nsl为非线性接触弹簧个数。
需要说明的是底座板与桥面在脱空处的相互作用属于局部应力分析范畴,一般情况下,该问题可基于有限元理论和接触算法进行求解,但是该计算方式的效率过低。因此为了提高计算效率,本文采用材料力学中的梁弯曲理论对该问题进行分析,导致计算结果存在一定误差,因此本文首先通过一个数值算例对该计算误差进行评估。
表1给出了采用有限元方法与本文研究方法的结果对比。在这两次计算中,结构尺寸、材料参数均相同,收缩徐变模型为JTG2012模型,收缩徐变时间为100年。从该结果中可以清楚看出,采用梁弯曲理论求解得到的底座板拉/压应力较之有限元方法大,但是结果差别不大,在误差接受范围之内。同时,采用梁弯曲理论求解该问题使计算效率大幅提高,因此本文后续计算中均采用该方法。

表1 有限元方法与本文研究方法的结果对比
2.3 高速车轨桥动力相互作用模型
建立考虑桥轨非线性接触和桥墩沉降的列车-轨道-桥梁动力学模型时遵循如下原则:
(1) 列车子模型考虑为一系列等间距放置在轨道上的车辆模型组成,基于多体动力学对车辆模型进行建模,每一节车辆考虑为一个车体、两个构架、四个轮对以及一、二系悬挂组成。
(2) 轨道子模型中的钢轨、轨道板以及底座板考虑为连续欧拉梁,建立其振动微分方程并借助Ritz法进行降维;扣件系统模拟为线弹性弹簧-阻尼元件;CA砂浆模拟为离散弹簧;在此需要对轨道板的建模方式进行解释,轨道板在布置时延纵向为断开的,但是布置结束后通过铰接以及二次浇筑的方式进行了二次连接,使轨道结构沿纵向形成整体,因此本文在建模时做了部分简化,将轨道板模拟为连续欧拉梁,该建模方式的有效性也得到了验证[13]。
(3) 本文采用我国高速铁路使用最多的32 m简支梁桥,采用有限元方法进行建模;支座考虑为节点自由度耦合;桥梁阻尼考虑为瑞利阻尼;本文共建立了4跨桥梁。
(4) 轮轨非线性接触模型采用非线性Hertz接触模型进行模拟。
该模型的详细方程和验证过程见文献[14]。
3 桥梁收缩徐变条件下轨道与桥面间非线性接触行为研究
本文采用的桥梁模型为32 m简支箱梁桥,其材料属性及截面见文献[15]。列车模型采用我国高速铁路上常见的车型CRH380A,其动力学参数见表1。
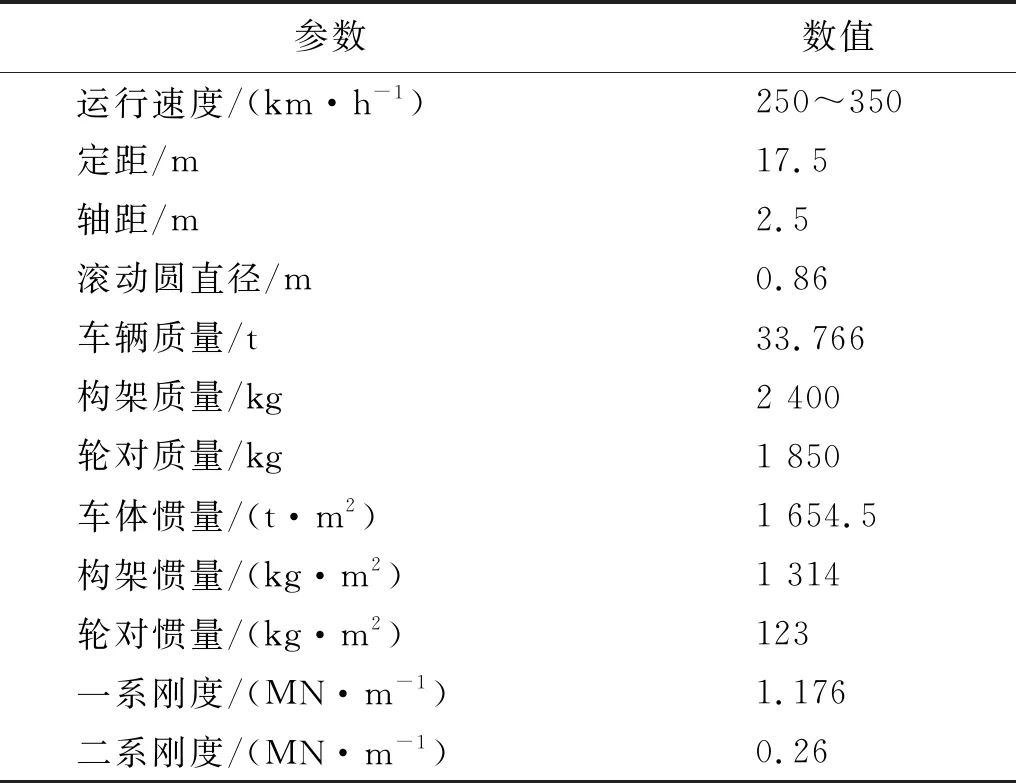
表2 高速列车动力学参数
采用第2.1节中的JTG2012收缩徐变模型,得到32 m简支箱梁的变形,如图3所示。由图3(a)可以看出,随着时间的增长,收缩徐变引起的桥梁变形趋于稳定。当桥梁运营100年后,收缩徐变导致的桥梁最终残余变形约为6.85 mm。本文在后续研究中将采用该收缩徐变数据进行分析。

图3 收缩徐变下桥梁变形
当混凝土收缩徐变引起桥梁变形后,轨道和桥面之间的非线性接触力分布如图4所示。
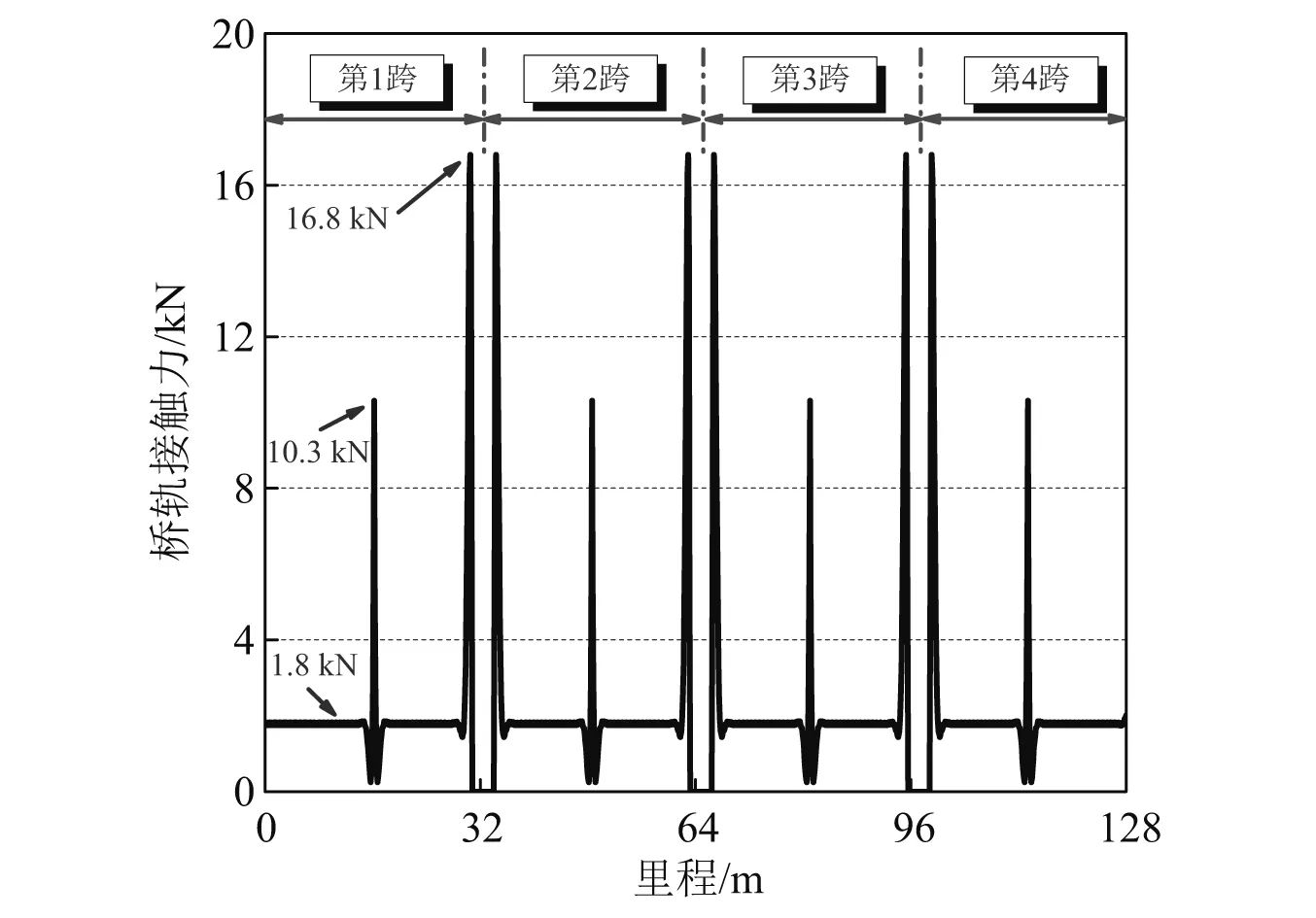
图4 轨道和桥面间非线性接触力分布
由该接触力分布可以清楚地看出,只有梁端处出现了接触力为0的情况,也就是说只有在梁端处才出现了底座和桥面间的脱空现象。另外值得注意的是,在跨中位置处接触力也仅有0.2 kN,表明跨中位置处尚未脱空,但是如果收缩徐变引起的桥梁变形继续增大则极有可能引起跨中位置也出现脱空现象。
桥梁收缩徐变导致底座和桥面在脱空的边缘位置处产生了非常大的接触力,达到16.8 kN,而普通区域处的接触力仅有1.8 kN,收缩徐变导致的脱空引起接触力增大了9.3倍。与此同时跨中位置处的接触力也增大了5.7倍。这一结果表明收缩徐变对梁端脱空附近的桥轨作用产生了巨大的影响。但是需要说明的是,即使收缩徐变没有导致跨中处的脱空,但是其对跨中位置处桥轨相互作用的影响则是不可忽略的。
当列车以250 km/h的速度通过时,桥轨之间的接触力,如图5所示。该图由三维图形及底部投影云图组成。从图中可以清楚地看出,列车动荷载引起接触力的明显增大,同时也导致脱空区域发生明显变化。列车荷载对脱空附近接触力的影响要大于其他部分。
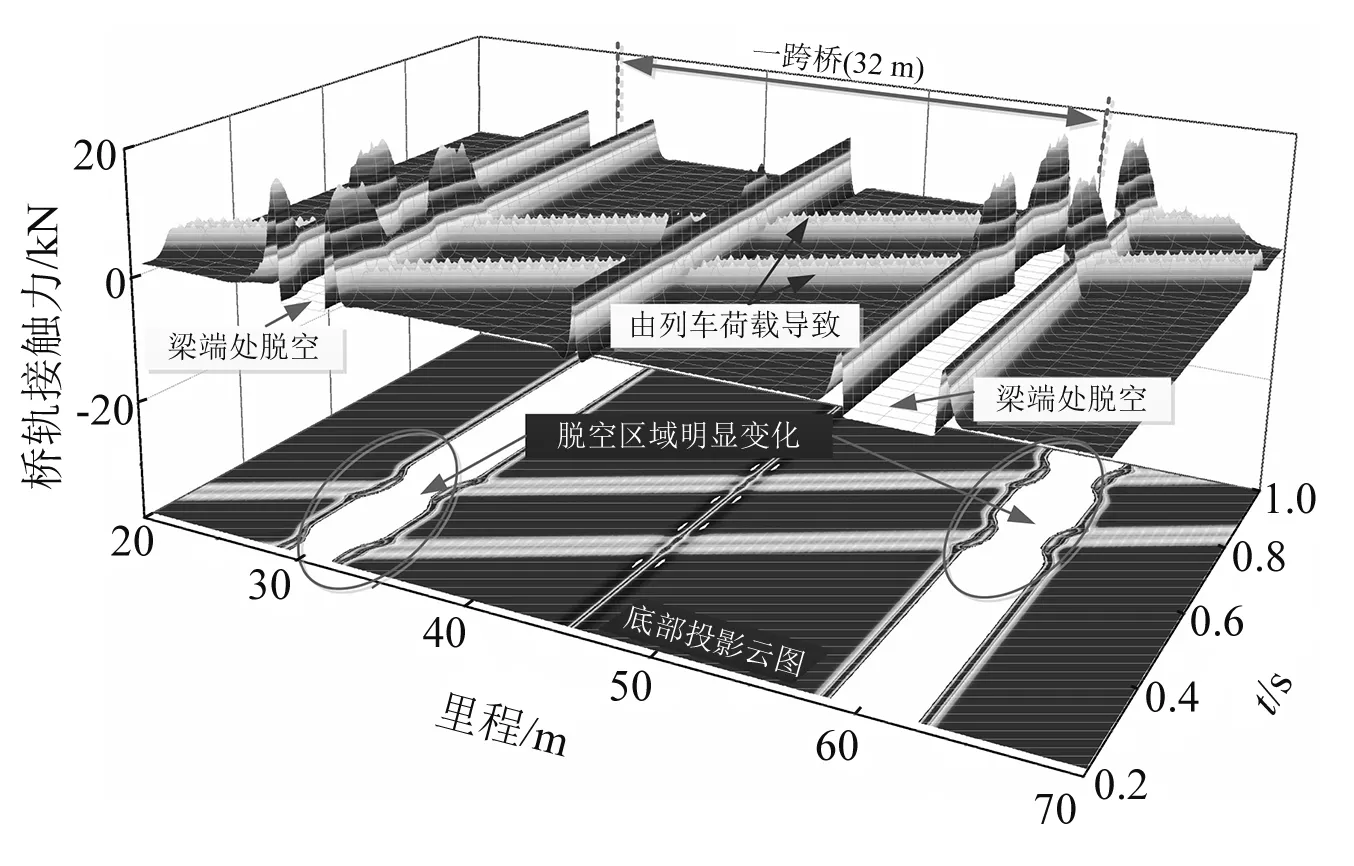
图5 桥轨之间非线性动态接触力(v=250 km/h)
为了更清晰地展示列车通过时脱空区域的变化情况,图6给出了脱空区域长度随时间的变化。从中可以看出,列车通过时脱空区域发生明显变化,脱空最大长度与最小长度之比约1.55。脱空区域的两个边界线的变化规律较为一致,不过由于距离的原因存在一定的时间延迟效应。需要说明的是,单个轮对对结果的影响不能清晰分辨,每一个转向架通过时会产生一个完整的变化过程,表明轮载作用在自上向下传递过程中有一定的削弱。
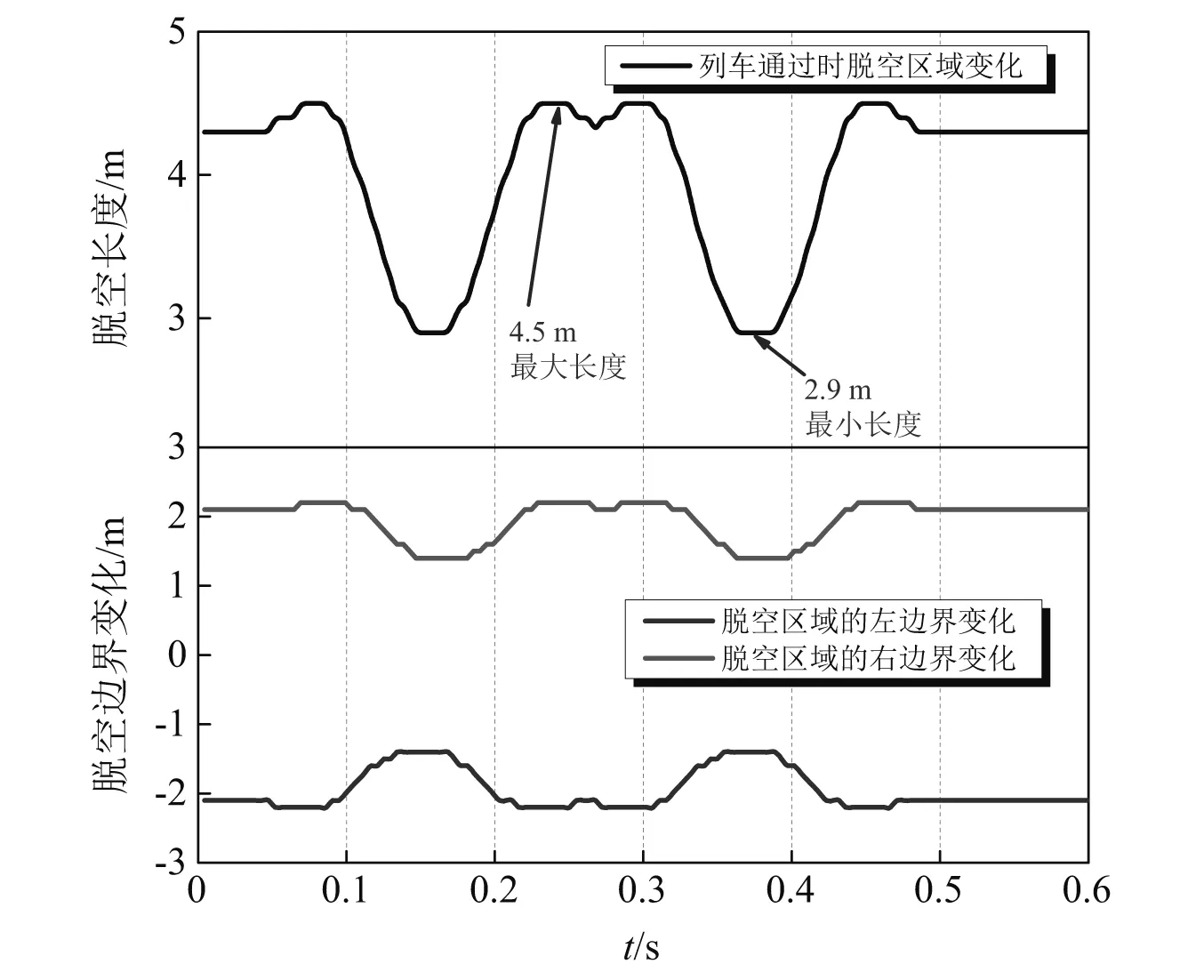
图6 脱空区域长度变化
考虑不同的行车速度,纵连板式轨道与桥面之间的脱空长度变化,如图7所示。该结果表明虽然随着速度的增大,脱空区域长度变化范围有了一定的增大,但是整体来看脱空区域长度对速度并不敏感。
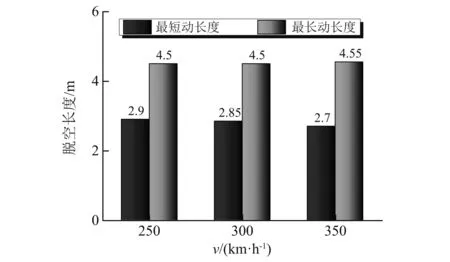
图7 不同速度下的脱空长度
4 桥梁收缩徐变条件下轨道层间动力相互作用研究
收缩徐变引起的桥梁变形会导致轨道结构竖向弯曲,并直接诱发轨道层间力(扣件力和砂浆力)的剧烈变化。当无列车通过时,收缩徐变导致的轨道层间力,如图8所示。从中可以看出梁端位置处的层间力有明显变化,砂浆力变化比扣件力剧烈。相比之下,跨中位置的层间力较小,这是由于桥轨在跨中处的剧烈接触力大部分由底座板承受。
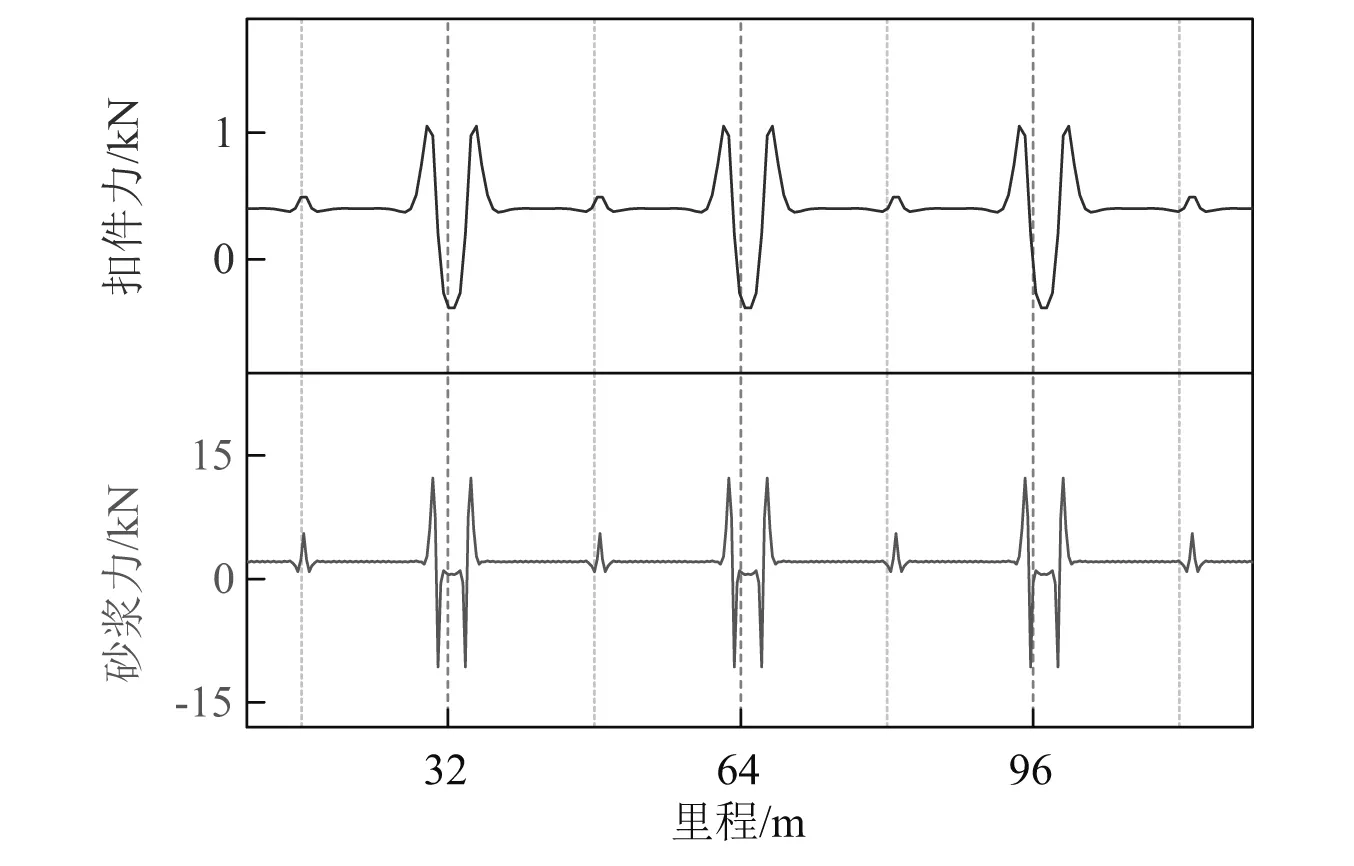
图8 收缩徐变导致的轨道层间力分布
更进一步,不同速度下脱空区域的轨道层间力变化情况,如图9所示。砂浆力和扣件力的变化相近,均呈现出较大的轮载效应。随着速度的增大,层间力均有一定的增大。另外需要说明的是,在列车行驶过去之后,轨道层间力降低至很小的数值,表明脱空区域的层间力并未收到收缩徐变的影响,同时也从侧面表明脱空区域的底座受力非常严峻。
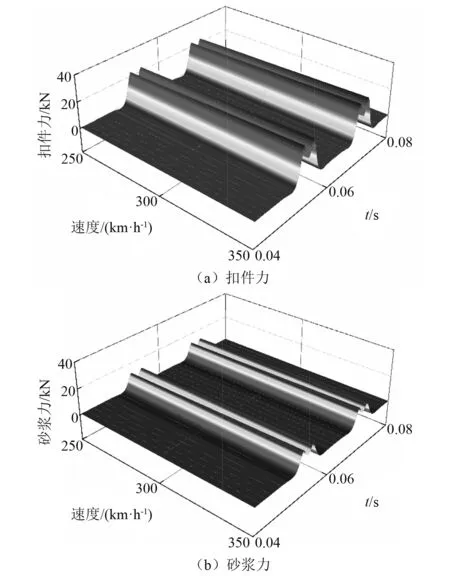
图9 不同速度下脱空区域的轨道层间力变化
5 桥梁收缩徐变条件下轨道混凝土结构附加应力研究
桥梁在收缩徐变效应下发生变形,进而导致纵连板式轨道上拱,也就直接导致结构内部产生了巨大的附加应力,本节将针对轨道混凝土结构(轨道板和底座)内部附加应力进行研究。
需要说明的是,本文建立的力学模型中轨道板和底座考虑为梁结构,因此不能直接提取其应力分布情况。本文首先提取各结构的振动位移,然后借助材料力学中梁的弯曲变形、弯矩和应力之间的关系进一步计算了轨道混凝土结构的应力。
由于底座和轨道板均为规则矩形截面结构,其最大拉/压应力会发生在上表面或下表面,因此下面也主要针对轨道板和底座上下表面的应力进行研究。同时通过轨道结构变形状态可以看出,轨道板和底座上表面在跨中位置承受拉应力,而下表面则在脱空位置(桥墩位置)处承受拉应力。由于混凝土结构不能承受较大拉应力,本文着重关注轨道板和底座的受拉区域。根据《混凝土结构设计规范》(GB 50010—2010)中的规定,轨道板和底座的抗拉强度分别为2.74 MPa和2.01 MPa。不过需要说明的是,底座板和轨道板内部均有钢筋加强,其局部能承受的拉压力强度要比上述两抗拉强度更大。不过本文为了更为严苛地对收缩徐变下的轨道应力进行评估,在后续计算中仍然选取的是2.74 MPa和2.01 MPa。
图10给出了收缩徐变导致轨道结构附加静拉应力情况,从中可以看出轨道板上表面主要以受拉为主,仅在脱空区域附近才出现局部受压,最大拉应力为0.42 MPa,最大压应力为0.79 MPa;而轨道板下表面的应力与上表面呈相反的分布状态,且最大拉应力均在安全范围之内。对于底座板来说,其应力分布规律与轨道板相似,不过其最大拉应力达到了1.19 MPa,也在国家标准规定的安全范围之内。另外,从该结果也可以清楚地看出,轨道板和底座位于桥墩位置处的下表面拉应力更值得关注。
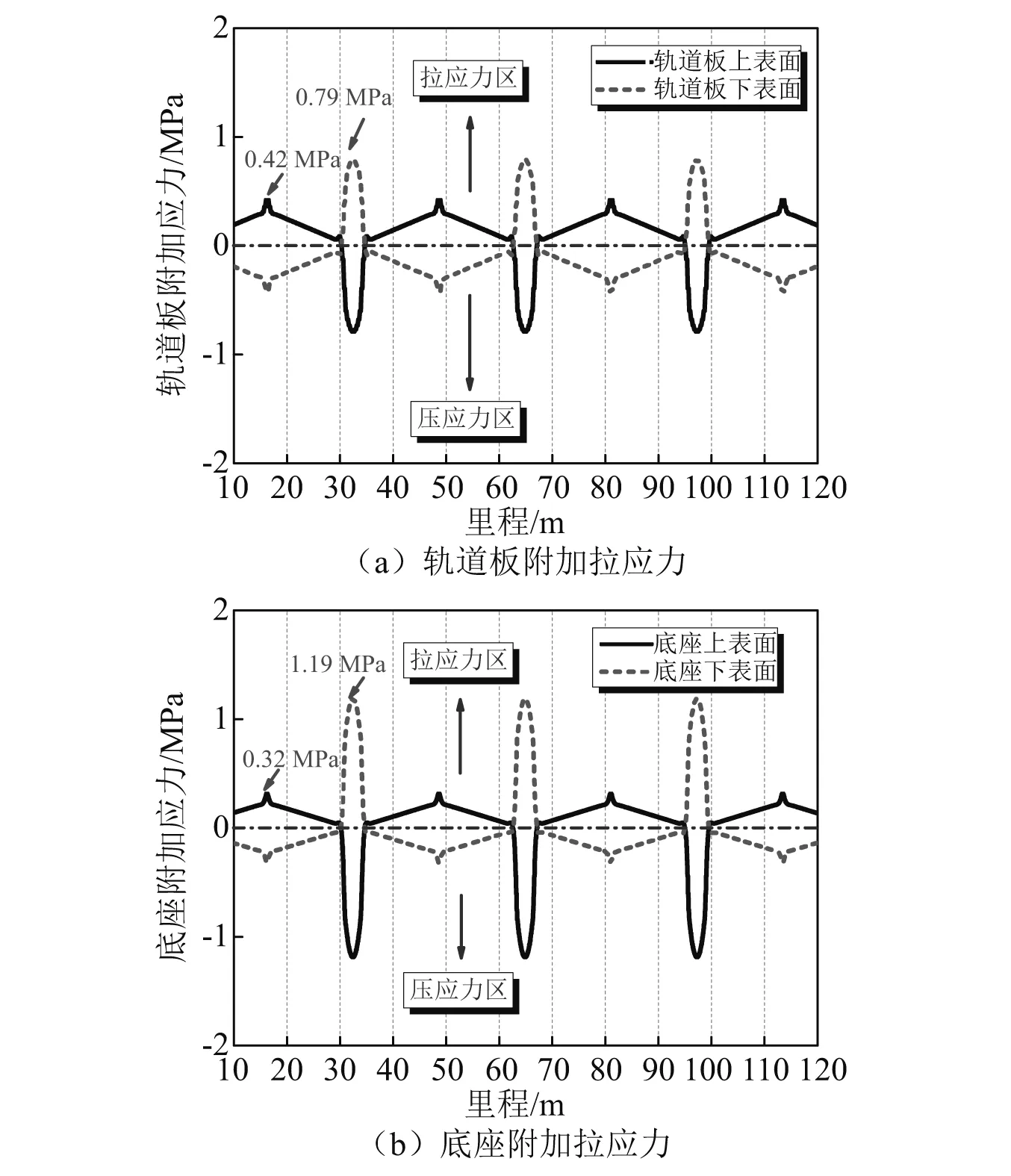
图10 轨道混凝土结构附加应力
在此基础上考虑列车动态特性,图11给出了列车荷载以及桥梁收缩徐变变形综合作用下轨道混凝土结构的拉应力情况。从中可以看出,随着行车速度的提高,底座和轨道板承受的拉应力均呈现增加的趋势,但是变化幅度较小,表明轨道结构附加应力对列车运行速度并不敏感。同时,从数值上来看,轨道混凝土结构在收缩徐变条件下仍具有较大的安全余量,表明桥梁收缩徐变作用下的轨道结构稳定性及安全性可以得到保障。
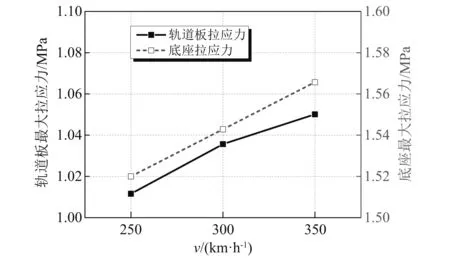
图11 列车荷载下轨道结构附加动应力
6 桥梁收缩徐变条件下车轨桥系统动态特性研究
收缩徐变导致桥梁变形,直接导致桥轨之间的脱空现象,进而影响系统的动态特性。当列车以350 km/h的速度通过收缩徐变区域时系统的典型动态特性,如图12所示。从中可以看出,收缩徐变效应主要影响列车的振动,而对轨下结构的振动影响较小。该结论也可以和既有研究成果相互验证。
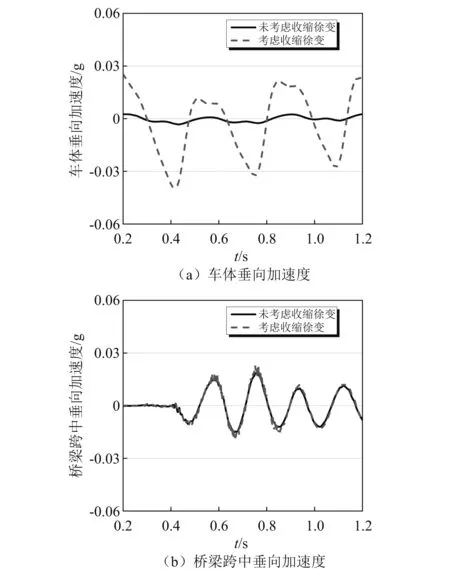
图12 车桥系统的典型波形对比
不同行驶速度下列车通过收缩徐变区域时的动态特性,如图13所示。从图中可以看出,随着行车速度的提高,车体加速度、轮重减载率、轮轨力最大值均随之增大,但是轮轨力最小值则呈现非线性下降的趋势。在所有动力学指标中,车体加速度对速度不太敏感,这是由于收缩徐变导致的长波激励对车体的影响更大导致的。轮重减载率对速度最为敏感,在脱空区域附近出现了较大的减载情况。而轮轨力最小值逐渐减小则说明了列车通过收缩徐变区域时受到基础的冲击,导致列车减载的趋势,这也是轮重减载率变化剧烈的原因。
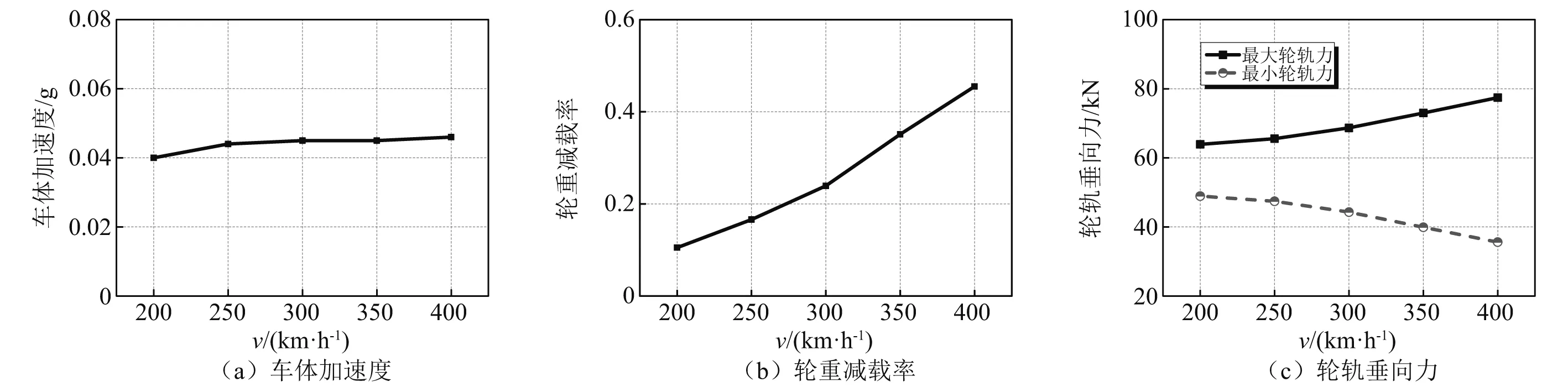
图13 不同速度下列车通过收缩徐变区域时的动态特性
7 结 论
针对高速铁路混凝土桥梁收缩徐变这一实际工程问题,本文深入研究了其引起的高速列车-CRTS Ⅱ型板式轨道-桥梁系统动力相互作用问题。通过本文研究可以得到如下结论:
(1) 本文提出的研究方法可以有效地研究收缩徐变条件下高速列车-纵连板式轨道-桥梁结构的动力相互作用问题。
(2) 收缩徐变导致梁端处出现了底座和桥面间的局部脱空;列车动荷载引起接触力明显增大;脱空区域长度对行车速度并不敏感;列车荷载对脱空附近桥轨接触力的影响要大于其他位置。
(3) 梁端附近的轨道层间力有明显变化,砂浆力变化比扣件力剧烈;脱空区域内的轨道层间力并未明显受到收缩徐变效应的影响;轨道附加动应力对行车速度不敏感;在本文研究参数范围内,桥梁收缩徐变下的轨道结构稳定性可以得到保障。
(4) 收缩徐变效应主要影响列车的振动,而对轨下结构的振动影响较小。
本文研究结论可以为我国高速铁路轨道工程的前期设计及后期运维提供一定的理论依据。
