基于改进小波阈值函数的安全阀排放声信号降噪
2021-06-30李树勋王志辉康云星侯建军
李树勋, 王志辉, 康云星, 侯建军
(1.兰州理工大学 石油化工学院,兰州 730050;2.兰州理工大学 机械工业泵及特殊阀门工程研究中心,兰州 730050)
随着西气东输、中俄“通气”等能源项目的实施,各类安全阀需求快速上升。安全阀作为设备及管路系统安全保护的重要屏障,是保证系统安全运行的关键所在。安全阀排放声信号可表征安全阀是否正常工作[1-2],因此,有效的消除该信号的背景噪声,对准确分析安全阀信号具有重要的意义。
近年来,国内外学者对信号降噪做了大量研究,提出了不同的降噪方法。文献[3]研究了一种新的小波降噪方法,提出选取分解层数的主客观算法,提高了降噪后的信噪比与计算速度。文献[4]提出小波与经验模态分解相结合的方法提取发动机爆震信号,得出在提升爆震检测可靠性的同时,降低了计算时间。文献[5]基于广义S变换模时频矩阵法对局部放电特高频信号进行降噪,得出该方法具有好的噪声抑制与较低的幅值衰减。文献[6]提出基于SOSO增强算法的奇异值分解(singular value decomposition, SVD)法对轴承故障检测信号降噪,得出新方法可显著增强微弱脉冲信号且有效的对残留噪声进行降噪。其中,小波分析具有多分辨分析的特性,在时频两域都具有较好的局部化能力,是一种时间窗和频率窗都可以改变的时频局部化分析方法[7-9],更适合处理安全阀排放声信号。
尽管近年来许多文献广泛研究了在各领域小波降噪的问题,然而国内外很少有学者在阀门领域从事小波降噪的研究工作。鉴于阀门试验环境中存在多种声源信息,包括上游控制阀噪声、车间机械噪声、生活噪声等环境噪声,且试验场所并未设有消音室,因此传感器采集到的信号为多个声源信息混叠下的混合噪声,不相关的信号会干扰阀门的声信号分析,导致误判阀门运行情况。为获得安全阀的泄压信号,本文针对噪声试验获得的混合原始数据进行小波降噪,提出一种具有指数型函数衰减特性的小波阈值降噪方法,采取分层自适应阈值,构建改进的阈值函数,避免将小于阈值的小波系数置零,防止过度降噪,引入调节因子α,使得该函数可满足不同类型安全阀信号特征的降噪要求。通过仿真分析与试验分析均验证了该方法的有效性。
1 小波阈值降噪原理与阈值算法
1.1 小波阈值降噪原理
小波变换(wavelet transform, WT)和多分辨分析(multi resolution analysis, MRA)是小波阈值降噪的基础[10-12]。它的原理是将含噪信号进行小波变换后,若对应小波系数模值大,说明该小波系数中含有用信号较多、噪声占比较小;反之,若对应小波系数模值小,则主要为噪音信号。因此,可以根据对应小波系数的大小,来设置临界阈值λ,进行降噪。降噪步骤一般为3步:①对含噪信号进行小波变换;②保留最大尺度下低频近似信号的系数,而对其余尺度下高频细节信号的系数选择合适的阈值函数与阈值进行处理;③对处理后的小波系数进行小波逆变换,获取降噪后的信号。含噪信号的底层模型如式(1)所示:
S(t)=f(t)+σe(t)
(1)
式中:f(t)是原信号;e(t)为噪声信号;σ代表噪声水平。降噪目的就是将S(t)信号中的e(t)压缩抑制,尽可能的还原f(t)。
1.2 分层自适应阈值
噪声信号的小波系数在每一层分解尺度上都有所不同,会随分解尺度的增大而减小[13],但是传统的阈值选取算法并未考虑分解尺度的变化对阈值的影响,因此本文采取一种新的阈值选取方式。依据噪声能量在各层小波中所占比例不同,在每个高频细节尺度上选取不同的阈值,避免传统软、硬阈值过度降噪的缺点,以达到更好的降噪效果。采用无偏风险估计准则(rigrsure)[14]来获取最佳阈值, rigrsure是一种基于Stein的无偏似然估计原理的自适应阈值选择方法。一般而言,可将式(1)的数学模型视为N维随机向量模型,如式(2)所示:
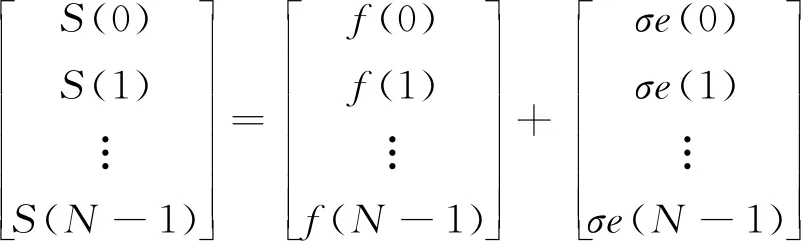
(2)
(3)
设W为一向量,其元素为式(3)小波分解系数的平方,并按照由小到大顺序排列,如式(4):
(4)
其中:w1≤w2≤…≤wn
设风险阈值向量T,其元素为:
(5)
式中:N为信号长度。
根据式(5)求得Tmin,根据min下标求得wmin,则 不同尺度上的阈值为:
(6)
式中:σj为不同尺度的噪声标准差。
(7)
式中:median( * )表示求解中值。
随着分解尺度的增加,噪声占比较大,求出的阈值相应较大,会使一部分有用信号系数被滤除,导致信号失真。本文依据文献[15]的方法,对阈值算法做出改进:
(8)
式中:j为分解层数。由式(8)可以看出,根据分解层数的变化,每一层都可自适应的得出最优阈值,不仅保留了噪声标准差及小波系数长度对阈值的影响,还额外考虑了分解尺度对阈值选择的影响,使得阈值随着分解尺度增加而减小,满足了噪声信号的小波系数随分解尺度的增大而减小的特点,具有更好的降噪效果。
2 改进的小波阈值函数
安全阀排放声信号的真实信号被淹没在机械背景噪声中,信噪比很低。针对软、硬阈值函数的不足,改进的阈值函数应在保证连续性的同时,对小于λ的小波系数不直接置零,保留接近阈值的一部分小波系数,尽可能多的保留声信号的有用部分,防止过度降噪。为此本文提出了一种改进的阈值函数,利用指数型函数的衰减特性,调整指数型函数的参数,对阈值函数的陡峭程度进行调整,使得接近阈值时函数曲线变换缓慢,远离阈值时函数曲线迅速陡峭,尽可能多的保留接近小波阈值的一部分小波系数,防止对安全阀排放声信号过度降噪,保留信号的完整性。改进阈值函数如式(9)所示:
(9)
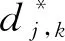
当|dj,k|>λ时,真实信号的小波系数较大,且噪声的小波系数相比真实小波系数占比很小,可以忽略,为保证降噪后信号更加贴合真实信号,在|dj,k|>λ时采用硬阈值函数降噪;当|dj,k|<λ时,提出一种指数型函数,使得λ与小波系数接近时,能够保留该部分小波系数,随着小波系数的减小,此时噪声信号占比大,由于指数型函数快速衰减的特性,该部分小波系数基本被滤除;此外引入调节因子α,使得改进阈值函数可根据不同信号特征基于软、硬阈值进行调整,让该函数模型更加灵活,提高函数的自适应性。改进阈值函数在调节因子α=0.15、0.5、1时的函数曲线与软、硬阈值函数曲线比较见图1。

图1 阈值函数特性比较
对改进阈值函数进行连续性检验,首先验证正半轴dj,k=λ处的连续性:
当dj,k→λ+时,右边:
(10)
当dj,k→λ-时,左边:
(11)
左边=右边,式(10)、(11)相等,故改进阈值函数在dj,k=λ处连续。同理可得改进阈值函数在dj,k=-λ处连续。
综上,改进阈值函数在正负阈值处都连续,因此改进阈值函数是连续的,避免在信号重构时发生震荡,产生Gibbs现象。
3 仿真试验与分析
为验证笔者提出的降噪方法的有效性,且具有一般性,设计振荡衰减仿真信号进行降噪分析。仿真信号的表达式为
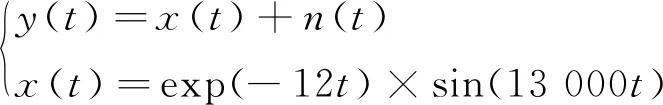
(12)
式中:t=[0,0.6],时间间隔为 0.000 9 s;n(t)为信噪比15 dB的随机噪声。
图2、3为原始信号与含噪信号的时域图、频域图。

图2 原始信号时域图、频域图
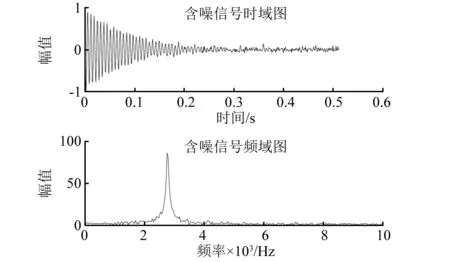
图3 加噪信号时域图、频域图
采用软、硬阈值以及改进阈值函数对仿真信号降噪,仿真试验经反复试算取分解层数为2层,阈值算法为极大极小阈值(Minimaxi),小波基函数选择sym6;图4、5为经三种阈值函数降噪后的信号。
图4、5可以看出:硬阈值函数降噪后时域信号在t=0.21、t=0.48等处存在尖峰现象,产生信号失真,降噪效果不理想。软阈值函数降噪后,时域信号较为光滑,但由于软阈值函数有固定的收缩性,且频域信号在2 200 Hz、3 310 Hz、7 200 Hz处与原信号频域图相比有较大重构失真,降噪效果不理想;改进阈值函数降噪后, 时域、频域信号都与原始信号最接近,重构精度高。

图4 不同阈值函数降噪时域图
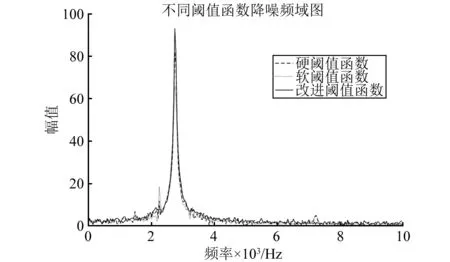
图5 不同阈值函数降噪频域图
本文以信号降噪后的信噪比(signal noise ratio, SNR)与均方根误差(root mean square error, RMSE)[16-17]作为降噪效果的评判标准,信噪比越大,均方根误差值越小,降噪效果越好。SNR与RSME计算式分别为:
(13)
(14)
式中:x(t)为含噪信号;d(t)为降噪后信号;n为含噪信号长度。表1为不同阈值函数降噪效果的对比。
由表1可知:根据降噪评判准则,改进阈值函数与软、硬阈值函数比较,SNR分别提高了11.89 dB、7.53 dB左右,RSME分别降低了了0.043、0.020 2,表明改进阈值函数降噪方法具有良好的降噪效果。

表1 仿真信号降噪后SNR与RSME
4 试验验证与分析
4.1 试验对象及其基本参数
测试所用安全阀结构如图6所示,基本参数如表2所示。

图6 试验所用安全阀结构图

表2 安全阀基本参数
4.2 安全阀排放声信号采集
为了验证改进阈值函数对安全阀实测信号降噪的有效性,笔者设计了一种弹簧载荷式安全阀噪声测试系统获取排放声信号,该噪声测试系统试验流程如图7所示;噪声测试系统主要由测试装置(气源、控制阀、稳压罐、被测安全阀)、信号采集装置(精密传声器、超高频动态采集仪)、PC终端组成。安全阀排放声信号采集时,首先启动压缩机将安全阀入口压力升至0.61 MPa,保持升压速率不超过0.01 MPa/s,持续缓慢升压至安全阀处于全开泄放下的压力0.72 MPa,设置测试系统中超高频动态采集仪的采样频率为10 000 Hz,采样数为1 024来采集安全阀排放声信号。图8为测试系统试验现场图。
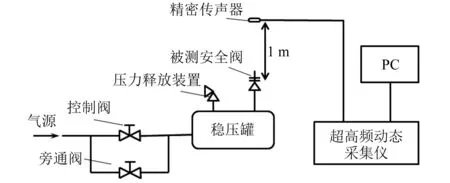
图7 噪声测试系统流程图

图8 噪声测试系统现场图
对实测信号进行快速傅里叶变换 (fast fourier transform, FFT)与小波时频谱分析,得到信号不同时间对应的频率关系。图9为实测信号的时频图与时频谱图。
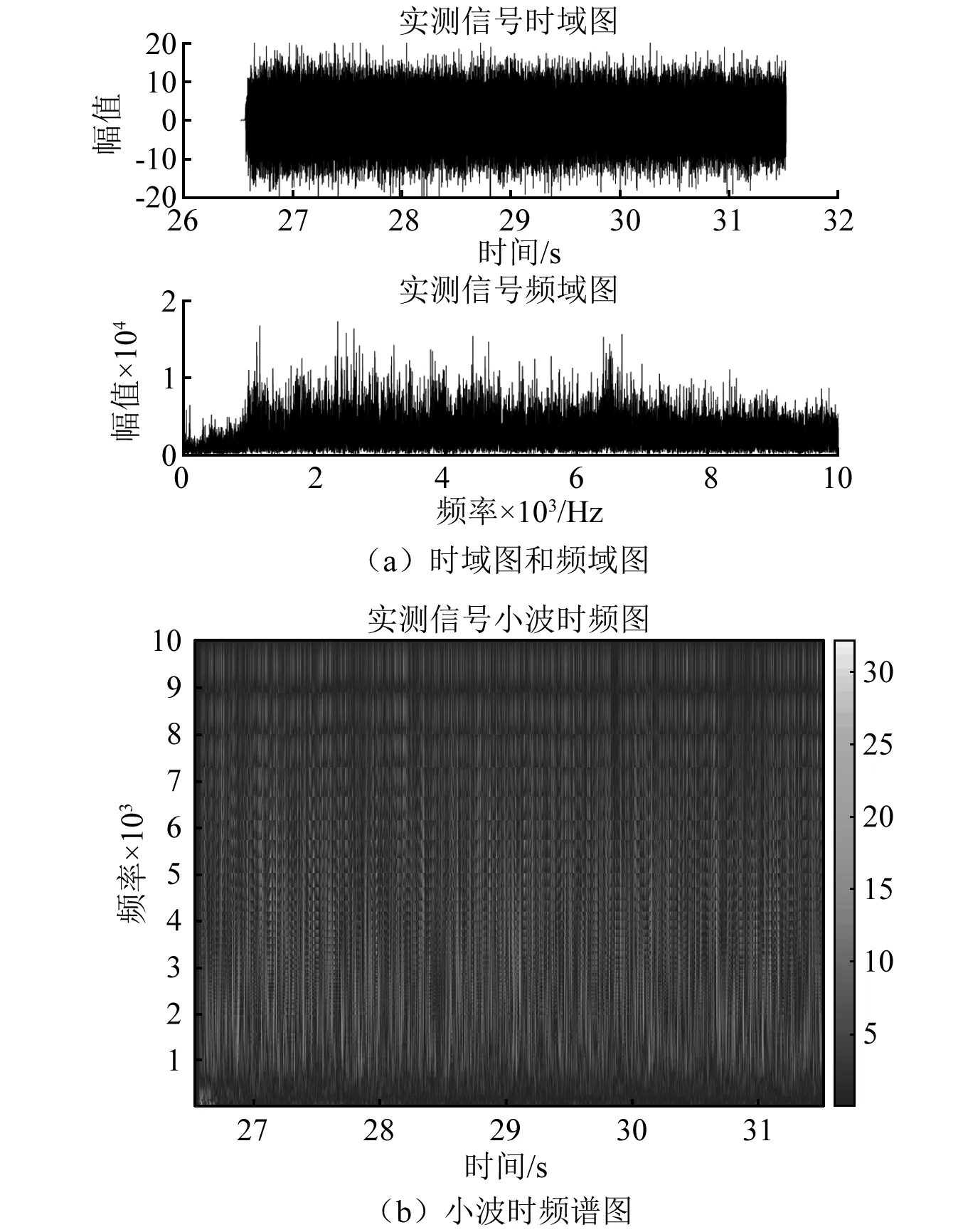
图9 安全阀实测信号图
由图9(a)可知:采集的实测信号中由于试验区周边压缩机、上游控制阀等机械噪声,车间环境噪声的干扰,严重污染了安全阀泄压信号,且该噪声为宽频的高斯噪声,对安全阀声源信息分析造成了较大的干扰。
4.3 Butterworth滤波降噪对安全阀声信号降噪
安全阀排放声信号主要集中在6 000 Hz以下的中低频段[18-19],因此采用典型的低通Butterworth数字滤波器对安全阀排放声信号进行降噪分析。设置低通截止频率为6 000 Hz,阻带截止频率为6 500 Hz,降噪效果如图10所示。

图10 滤波降噪后信号时域图和频域图
由图10可知,对安全阀排放声信号采用滤波器降噪后,完整的保留了低通截止频率之前的信号,且对保留下来的信号并未降噪处理,对低通截止频率之后的信号完全滤除,导致了安全阀信号不完整,失真等缺陷,降噪效果不理想。
4.4 阈值函数降噪法对安全阀声信号降噪
对实测信号采取不同阈值函数降噪,并对降噪后信号进行小波时频谱处理,对比分析新方法的有效性。仿真试验选取调节因子α=0.15、分解层数4,表3为不同分解层数对实测信号降噪的影响;经过四种不同阈值算法筛选比较,采用无偏似然估计阈值(Rigrsure),表4为四种阈值算法的对降噪的影响;为避免信号在多尺度分解和重构中边缘部分较大失真,采用具有对称性或近似对称性的双正交小波基;为避免信号突变,要求小波基有良好正则性和较小消失距[20-21]。因此,选择以下三种同时具有近似对称性、较小消失矩阵、及正则性的小波基symN(N=2,3,…,8),dbN(N=2,3,…,10),coifN(N=2,3,…,5)。经筛选,选取db6为小波基函数;表5为不同小波基函数对降噪的影响。
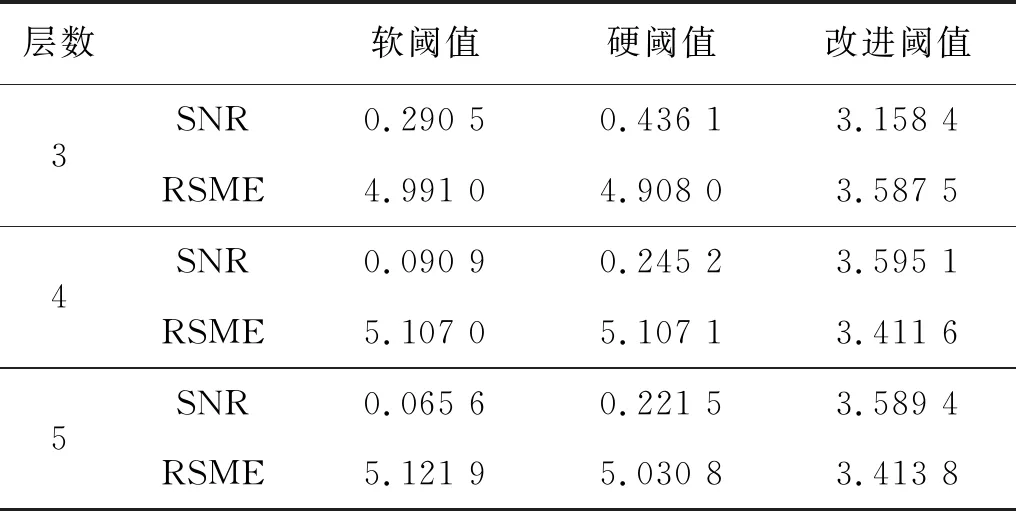
表3 不同分解层数对降噪的影响

表4 四种阈值算法对降噪的影响

表5 不同小波基函数对降噪的影响
由表3可得:当分解层数为4时,通过改进阈值函数降噪后的信噪比最大,均方根误差更小;由表4可知:当阈值算法为Rigrsure时降噪效果要明显优于其它三种阈值算法;由表5可知:选择db6为小波基函数时,降噪后的信噪比更大,且有更小的均方根误差。图11~13为安全阀实测信号经三种阈值函数降噪后的时域图、频域图及小波时频谱图。

图11 软阈值函数降噪图
由图11可以看出:软阈值降噪后,只保留了频率fs在1 000 Hz左右的低频信号,对比图11(b)小波时频谱图,信号频率fs在1 000 Hz左右的低频信号保留较好,但在26.56~27.8 s、28.1~29.28 s、29.43~31.46 s三段时域范围内所对应6 000 Hz以下的频域范围信号过度降噪,信号失真严重,降噪效果不理想;由图12可看出:在信号频率fs<6 000 Hz时,硬阈值降噪效果要优于软阈值,保留了在422 Hz、2 260 Hz、3 453 Hz峰值处的有效信号,但信号幅值衰减严重;在频率fs>6 000 Hz时,形成一个宽频带的信号,结合图12(b)小波时频谱来看:在硬阈值降噪后,时域范围所对应的6 000 Hz以下的中低频段内虽然有信号,但在27.48~27.79 s、28.23~28.61 s、29.4~30.56 s及31.13~31.5 s这四个时域区间所对应的降噪后的频域范围失真严重,有用信号基本被滤除,降噪效果并不理想。由图13可得:改进阈值函数在信号频率范围内降噪效果明显,保留了在9 993.2 Hz、1 113 Hz、2 315 Hz、3 800 Hz、4 417 Hz、6 507 Hz、7 939 Hz等峰值处的信号,较好的还原了真实信号,且根据图13(b)小波时频谱也可看出,经改进阈值函数降噪后,在整个时域范围所对应的频域内,信号在6 000 Hz以下均有分布,降噪优于传统软硬阈值函数。改进阈值函数有效地抑制了高频部分有效信息的丢失,提高了重构信号的可信度。表6为三种阈值函数对实测信号降噪后信号的SNR与RSME。

图12 硬阈值函数降噪图
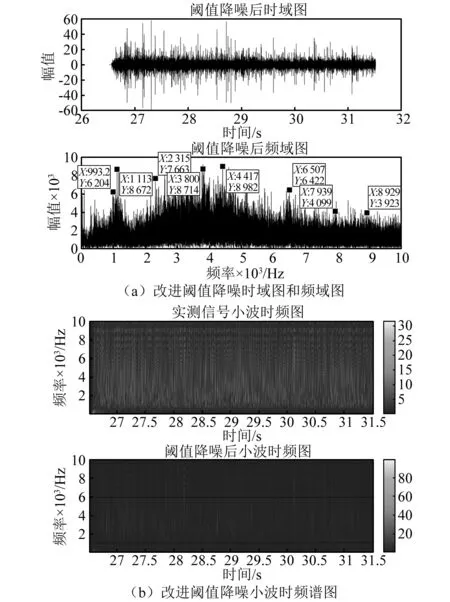
图13 改进阈值函数降噪图
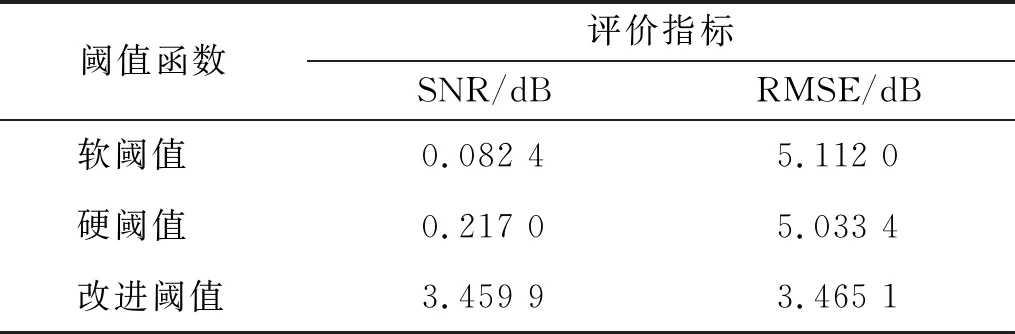
表6 阈值函数降噪后SNR和RSME比较
表6可以看出:改进阈值函数降噪后信号的SNR比软阈值提升了3.377 5,比硬阈值大了3.242 9,SNR有显著的提升;RMSE分别减小了1.646 9、1.568 3,因此改进阈值函数对安全阀排放声信号降噪的效果要明显优于传统的硬阈值和软阈值方法。
5 结 论
使用噪声测试系统采集安全阀排放声信号,在常规阈值降噪的基础上,提出一种分层自适应阈值函数降噪方法,对实测信号降噪,得出了以下结论:
(1) 对每一层高频细节信号上根据噪声能量占比自适应的选取最优阈值,改进阈值函数曲线是连续的,防止信号重构时产生Gibbs现象;改进了软、硬阈值函数将小于阈值的小波系数置零的缺点,避免一部分有用信号的丢失。
(2)该函数有效地保留了安全阀排放声信号高频部分的有用信息,且可改变调节因子α,进而改变阈值函数的收缩程度,具有一定的自适应性,可对不同类型安全阀信号进行处理。
(3)降噪结果表明:低通Butterworth滤波器仅保留了低通截止频率前的信号,且并未做降噪处理,降噪效果不理想;改进阈值函数降噪后,信号失真小,其信噪比相较软阈值增大了3.377 5 dB,相较硬阈值增大了3.242 9 dB,均方根误差分别减小了1.65、1.57左右,进而验证了本文提出的改进阈值数对安全阀排放声信号降噪的有效性。
