基于变分模态分解和最大重叠离散小波包变换的齿轮信号去噪方法
2021-06-30周小龙徐鑫莉刘薇娜姜振海马风雷
周小龙, 徐鑫莉, 王 尧, 刘薇娜, 姜振海, 马风雷
(1. 北华大学 机械工程学院,吉林 132021; 2. 上海交通大学 自动化系,上海 200240;3. 长春理工大学 机电工程学院,长春 130022; 4. 长春工业大学 机电工程学院,长春 130012)
齿轮作为最常用的传动装置被广泛应用于各类机械设备中。当齿轮出现故障时,会导致设备的整体性能下降,严重情况下会造成设备事故并带来巨大经济损失[1]。在实际工况中,齿轮工作环境十分恶劣,环境噪声和信号衰减等因素对于早期故障特征有较大影响,而齿轮早期故障特征比较微弱,往往淹没在强背景噪声中难以提取[2]。因此,对于齿轮故障信号去噪方法的研究具有重要意义。
相较于正常状态,齿轮的故障信号大多数是多分量的调幅-调频信号[3]且表现出非线性、非平稳性的特点。众多学者在该类信号降噪方面进行了大量研究。Huang等[4]提出的经验模态分解(empirical mode decomposition,EMD)方法是一种自适应信号处理方法,它能够根据信号的自身特性,将其分解成一些列表征信号特征的由高频到低频的固有模态函数(intrinsic mode function,IMF)分量。李琳等[5]将EMD方法应用于齿轮振动信号的去噪研究。邵忍平等[6]将EMD同小波分析方法相结合,提出一种基于EMD小波阈值的去噪方法,并有效实现了齿轮故障信号的去噪与故障特征提取。
然而,由于自身算法的限制,EMD方法在分解过程中易产生模态混叠问题,影响信号的去噪效果。Wu等[7]针对该问题,提出一种噪声辅助分解的集合经验模态分解(ensemble empirical mode decomposition,EEMD)方法。刘晓凰等[8]采用EEMD方法对齿轮振动信号进行去噪分析,并指出该方法去噪效果优于小波阈值和EMD去噪方法。宁少慧等[9]为避免EEMD去噪过程中信号特征信息丢失情况的产生,将时频峰值滤波技术引入EEMD齿轮信号去噪过程中,使得信号在噪声滤除和有效信号保真方面得到权衡。
实际计算中由于受限所添加白噪声的次数,EEMD分解过程中向信号内添加的噪声难以彻底消除,这将影响信号特征提取的准确性;同时,该方法的模态选取属于递归“筛选”,受采样频率影响较大,实际信号处理效果并不理想。近年来,Dragomiretskiy等[10]提出一种可变尺度的非平稳信号分析方法——变分模态分解(variational mode decomposition,VMD),此方法可将复杂信号分解为多个单分量调幅-调频信号和的形式,分解过程中的模态个数可自适应地确定,有效避免了模态混叠问题的产生,并表现出更好的噪声鲁棒性。因此,针对齿轮故障信号的特性,VMD方法相较于传统递归式分解方法,具有更强的适用性。
基于上述分析,为从含噪齿轮信号中有效提取相关故障特征信息,本文提出一种基于VMD和最大重叠离散小波包变换(maximal overlap discrete wavelet packet transform,MODWPT)相结合的去噪方法。通过仿真信号和实测数据的分析,结果表明,所提方法可有效滤除信号中的噪声干扰和迭代误差成分,实现信号特征的准确提取,为该类问题的解决提供了一种可行方法。
1 基本原理
1.1 VMD方法
VMD方法可根据预设尺度参数K将信号f分解成K阶中心频率为ωk的模态函数uk。则可得到变分约束问题:
(1)
式中:∂t为对函数求时间t的偏导数;δ(t)为单位脉冲函数。
引入增广拉格朗日函数ζ,将约束问题转化为非约束问题:
(2)
式中:α为惩罚因子,保证在高斯噪声存在情况下信号的重构精度;λ为拉格朗日乘子;<>表示向量内积。
则求得的模态分量uk及中心频率ωk分别为:
(3)
(4)
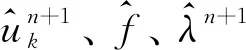

(5)
1.2 基于能量熵增量-频域互相关系数准则的敏感模态分量选取算法
当齿轮出现故障时,故障齿在啮合过程中,不仅会引起振动信号幅值和相位的变化,同时也会使振动信号的能量发生变化[11]。信号经VMD分解所得IMF分量的中心频率由低频至高频分布,具有不同的能量。表征信号自身特征信息的主模态分量应占有主要能量,而特征信息不敏感的虚假模态分量的能量所占比重较小[12]。时域互相关系数选取法是最为常用的信号内噪声干扰成分的判别方法[13]。当信号内存在噪声时,噪声干扰成分除影响信号自身特性外,还会影响时域互相关系数的计算精度。在频域内噪声成分的功率谱密度较小,且功率谱的互相关系数受噪声干扰小。
鉴于上述分析,在此以各IMF分量的能量熵增量和频域互相关系数值对表征信号特性的敏感模态分量进行选取[14]。
设u1(t),u2(t), …,un(t)为信号x(t)经VMD分解得到的IMF分量。基于IMF能量熵增量的敏感模态函数判别算法的具体过程如下:
(1)计算各IMF分量的能量E(ui(t)):

(6)
式中,ui(t)为第i阶IMF分量。
(2)求解各IMF分量的归一化能量p(i):
(7)
式中,N为IMF分量的总阶数。
(3)计算各IMF分量的能量熵增量值Δqi:
Δqi=-p(i)log2(p(i))
(8)
根据时域互相关系数计算方法,设Gx、Gy分别为信号xi和yi功率谱,fa为分析频率,则频域内信号xi和yi的互相关系数ρf可表示为:
(9)
式中:∣ρf∣越大,表明两信号在频域上相关性越好;反之,∣ρf∣越小,说明两信号在频域上相关性越差。
基于能量熵增量-频域互相关系数准则的敏感IMF分量选取算法以能量和频域互相关角度出发对敏感模态分量进行选取,所受干扰因素较少,能够更为有效地判别出表征故障信息的敏感IMF分量,弱化同故障信息无关的模态分量的影响。
1.3 MODWPT算法
通常表征高频噪声成分的IMF分量中,除包含噪声外,还含有部分表征信号特征的高频成分,若直接将这些高频成分作为噪声干扰滤除,可能会造成信号内关键信息的丢失,降低信号特征提取的准确性。为进一步提升信噪比和去噪效果,在此选用MODWPT方法对表征高频噪声的IMF分量进行分解降噪。
最大重叠离散小波变换[15](maximal overlap discrete wavelet transform,MODWT)可看作一经修改后的最大离散小波变换(discrete wavelet transform,DWT),它是一高度冗余的非正交小波变换,对样本容量N无要求。
MODWPT的分解系数可由Wj,n={Wj,n,t,t=0,…,N-1}表示,其中j为分解层数,n可看作一个随j变化的频率索引,则可计算出MODWPT的分解系数:
(10)
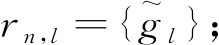
与传统DWT方法相比,MODWT具有小波系数和尺度系数的平移不变性、所有分解层数都保持相同时间分辨率、无相位扭曲等突出优点,非常适合处理非线性、非平稳信号。同时,如离散小波包变换(discrete wavelet packet transform,DWPT)可有效弥补离散小波变换无法对高频段进一步分解的缺陷一样,MODWPT不仅具有MODWT的所有优点,并可进一步对高频段进行分解,从而提高频率分辨率,达到有效滤除信号内高频噪声干扰成分的目的。
2 仿真分析
通常齿轮故障信号为一多分量调幅-调频信号,为更加真实地模拟齿轮的多分量振动信号,建立仿真信号z(t):
z(t)=x1(t)+x2(t)+x3(t)+y(t)
(11)
式中:x1(t)=[1+sin(40πt)]cos[400πt+2cos(40πt)];
x2(t)=0.8[1+sin(40πt)]cos[1 200πt+2cos(40πt)];
x3(t)=0.6[1+sin(40πt)]cos[2 000πt+4cos(40πt)]。y(t)为高斯白噪声信号。
信号采样频率为4 096 Hz,采样时长1 s,仿真信号z(t)的时域波形如图1所示。

图1 仿真信号z(t)时域图
2.1 VMD分解参数的选择方法
预设尺度参数K和惩罚因子α直接影响着VMD分解信号的准确性。目前智能搜寻算法虽可对上述参数值进行优化,但此类方法耗时较长,难以达到实际检测的目的。为此,本文提出一种高效简便的VMD分解关键参数选择方法。
2.1.1 预设尺度数K的选取
信号经VMD分解所获得的各IMF分量的中心频率以由低频到高频的形式分布,若取得最优预设尺度数K,则各IMF分量间的中心频率分布较为合理,数值不会出现相近或重叠的现象。因此,目前研究人员多采用中心频率观察法用以确定预设尺度数K的最优值[16-17]。但由于缺乏定量的判定标准,致使预设尺度K的选取具有一定的主观性和经验性,在实际信号分析过程中缺乏普适性[18]。
由式(5)可知,VMD分解以相邻两次循环过程中IMF分量的频域变化作为迭代约束条件,用以判定分解迭代停止。鉴于此,本文以相邻两次分解过程中相同阶数模态分量间中心频率的数值变化作为预设尺度参数K的判定条件,用以确定其最优值。提出一种基于有效中心频率数量N的预设尺度K值选取算法。
该算法的主要步骤为:
步骤1 初始化K值,令K=2;
步骤2 对信号进行VMD分解,得到K阶IMF分量和每阶IMF分量的中心频率ωK,i(i= 1, 2,…,K);
步骤3 令K+1,对信号再次进行VMD分解,得到K+1阶IMF分量和每阶IMF分量的中心频率ωK+1,j(j= 1, 2,…,K+1);
步骤4 根据式(12)计算相同阶数不同分解次数下,各IMF分量中心频率的判定精度εK,k(k= 1, 2,…,K):
(12)
式中:ωK+1,k为预设尺度取K+1时,VMD分解所得第k阶IMF分量的中心频率;ωK,k为预设尺度取K时,VMD分解所得第k阶IMF分量的中心频率。
步骤5 判断判定精度εK,k与精度阈值θ(经大量试验θ取值为0.11)的大小。若εK,k≤θ,则认定其为有效中心频率,若εK,k>θ,则将其定为无效中心频率。设NK+1、NK分别为判定预设尺度取K+1和K时,从IMF1分量开始所获得的连续有效中心频率数量。
步骤6 若NK+1>NK,认为VMD分解不彻底,则重复步骤3 ~ 步骤5;
步骤7 若NK+1≤NK,即连续有效中心频率数量不再增加,则认为出现了疑似过分解,由此得到预设尺度的暂定最优值为K;
步骤8 设当前获得预设尺度的暂定最优值为K,若待分解信号本身含有多个不同频率分量,则仍有欠分解的可能性。为避免上述问题的产生,取K+2重复步骤3~步骤5,若NK+2≤NK+1,则最优预设尺度即为K;若NK+2>NK+1,则重复步骤3~步骤7,以获取第2个最优尺度的暂定值。假定NK+3≤NK+2,即K+2为算法获得第2个暂定最优值,则max{NK,NK+2}所对应的预设尺度参数即为最优值。
不同K值下对仿真信号分解得到各IMF分量的中心频率如表1所示。

表1 不同K值对应的各IMF分量中心频率
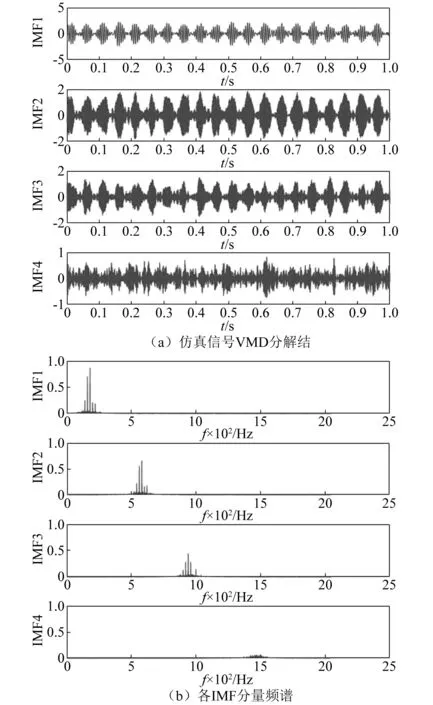
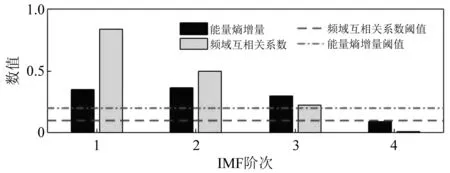
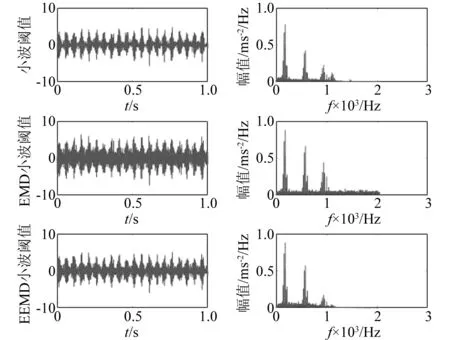
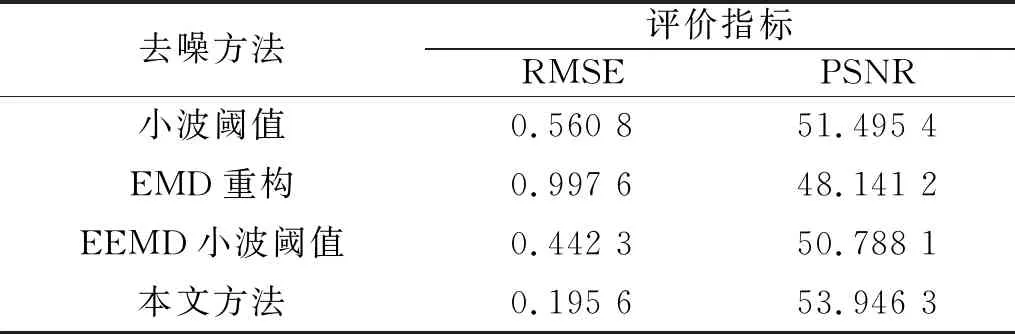
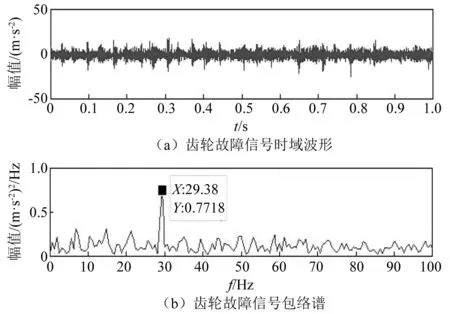
为确定预设尺度K的最优值,按本文所提方法分别计算K取不同值时各IMF分量的判定精度,计算结果如表2所示。由表2可知,N4=3>N5=1,由此可将K=4暂定为最优值,同时,N6=0 表2 不同K值对应的各IMF分量判定精度 将此方法应用于文献[16-17]所采用的美国西储凯斯大学的滚动轴承振动数据。通过分析可证明基于有效中心频率数量N的预设尺度K值选取算法的有效性,限于篇幅,在此仅列出文献[16]中表1轴承内圈故障信号在不同K值下对应各IMF分量判定精度的计算结果,见表3。 表3 不同K值下轴承内圈故障信号对应的各IMF分量判定精度 由表3可知,N2=1>N3=0,由此可将K=2暂定为最优值,同时,N4=4>N5=3,且N4>N2,故预尺度K的最优值为K=4。上述分析,验证了所提方法的有效性,也证明对于由多频率分量组成的信号,算法中步骤8的重要性。此外,文献[13]和文献[18]中实测滚动轴承及齿轮箱故障信号的分析亦可证明此方法的有效性,同时也说明此方法具有一定的普适性。 2.1.2 惩罚因子α的选取 惩罚因子α的选取决定了VMD分解得到的各IMF分量的带宽,α越小则IMF分量的带宽越大,反之,各IMF分量的带宽越小。 由于VMD算法具有较好的噪声鲁棒性,在采用VMD方法对采集到的故障信号进行分解后,信号内的背景干扰和环境噪声成分应得到一定滤除,信号内包含较多同故障特征相关的冲击成分,呈现较强的规则性和自相似性。模糊熵是评价非平稳信号复杂程度的重要参数,同样本熵、近似熵等方法相比,模糊熵值随相关参数的影响较小、稳定性强。正常工况下齿轮振动是随机振动,信号的无规则程度和复杂性较高,自相似性较低;当出现故障时,其振动信号内的冲击成分增加,信号的规则性和自相似性增强。 基于上述分析,当采用VMD方法对齿轮故障信号进行分解后,若α取得最优值,信号内的冲击成分、规则性和自相似性都应得到增强,故重构信号的模糊熵值应为最小。为准确刻画信号的复杂程度,在此选用模糊熵值作为惩罚因子α的选取评价参数。 当K=4时,计算惩罚因子α在不同取值范围下,重构信号的模糊熵值,结果示于图2。计算过程中,模糊熵值的嵌入维数m=2、相似容限r=0.15SD(待分解信号的标准差)。 图2 惩罚因子α与重构信号模糊熵值间的关系 由图2可知,当α=3 300,经VMD分解后重构信号的模糊熵值最小,由此说明重构信号内同故障特征相关的冲击成分所含最多,呈现较强的规则性和自相似性,故取惩罚因子α=3 300对仿真信号进行分解。 根据相关参数选择算法,仿真信号的VMD分解结果及各IMF分量的频谱如图3所示。 图3 VMD分解结果及各IMF分量频谱 由图3可知,VMD方法的分解结果较为合理,其中IMF1~IMF3为调幅-调频信号,IMF4为高频高斯白噪声成分。IMF1~IMF3分量主要集中在其中心频率附近,验证了所提参数选取方法可有效抑制分解过程中产生的模态混叠问题,减少各模态分量间的信息泄露。但也可看到,表征高频噪声模态分量的时域波形中存在着一定的冲击特性,由此表明所分解出的高频噪声分量中也包含着一定信号特征信息,在滤除信号内所含噪声的同时,应对这些特征信息进行有效提取和还原。 计算各IMF分量的能量熵增量及其同原信号间的频域互相关系数,对于虚假IMF分量的判别,时域互相关系数阈值常设为0.1,或设置为时域互相关系数最大值的0.1倍[19],故在此将频域互相关系数ρf的阈值设置为0.1;同时,为避免频域相关系数阈值选取可能无法有效滤除表征低频噪声并包含少量故障信息的虚假IMF分量,在此将能量熵增量Δqi的判别阈值设置至0.2。计算结果如图4所示。 图4 各IMF分量的能量熵增量和频域互相关系数 由图4可知,各IMF分量的能量熵增量和频域互相关系数判别结果得到的敏感分量为IMF1~IMF3。由之前分析可知,IMF4为向信号内添加的噪声干扰成分。因此,基于能量熵增量-频域互相关系数准则的敏感IMF分量选取算法可有效剔除VMD分解得到的同信号故障特征无关的虚假干扰成分。 采用MODWPT对噪声分量IMF4进行分解,参考文献[15]并通过对仿真信号的分析,在分解过程中选择长度L=22的Fejer-Korovkin小波滤波器,分解层数J=4,分解所得低频分量,如图5所示。 图5 IMF4分量的MODWPT分解结果 由图5可知,高频噪声分量IMF4经MODWPT分解后,其频率最低分量C1中的噪声干扰成分得到有效滤除,信号的冲击特征较为明显,由于噪声成分多集中在高频域内,因此,将C1分量作为高频去噪分量与VMD分解所得IMF1~IMF3分量进行重构,重构后去噪信号和无噪声存在情况下仿真信号的时域波形和频谱如图6所示。 由图1和图6可知,仿真信号z(t)经本文方法处理后,重构信号内绝大多数无用的干扰和噪声成分得到有效滤除,信号时域波形和频谱图可有效突显信号x(t)的特征信息。 图6 不含噪仿真信号和去噪重构信号的时域波形和频谱 为说明本文所提方法的有效性和优越性,分别采用小波阈值、EMD重构降噪[20]和EEMD小波阈值去噪法[21]对含噪信号z(t)进行去噪处理,去噪结果如图7所示。其中,小波阈值去噪时采用db6小波基和“Rigrsure”规则进行软阈值降噪。 图7 不同去噪方法对信号z(t)的去噪效果 由图7可知,小波阈值、EMD重构降噪和EEMD小波阈值去噪法的去噪效果并不理想,去噪后信号内仍有大量噪声残留,这势必会影响后续信号分析效果。 为定量评价各种方法的优劣,采用均方误差(root mean squared error,RMSE)和峰值信噪比(peak signal-to-noise ration,PSNR)作为去噪效果评价指标。其对应计算公式为: (13) (14) 式中:x(t)为仿真信号;x′(t)为去噪后信号。 由图6、图7和表4的对比,证明了本文所提方法的有效性,相较于小波阈值去噪、EMD重构降噪和EEMD小波阈值去噪法,本文方法在去噪效果和性能指标上都明显优于上述方法。 表4 不同方法去噪效果评价指标对比 针对齿轮实际工况复杂、常伴随噪声干扰致使故障特征难以提取的问题,根据仿真分析结果并结合VMD和MODWPT各自方法的优点,本文提出的基于VMD-MODWPT的去噪方法具体步骤如下: 步骤1 采用VMD方法对齿轮故障信号进行分解,根据有效中心频率数量N的预设尺度K值选取算法确定预设尺度K的最优值。 步骤2 在选定最优预设尺度K值后,计算惩罚因子α在不同取值范围下,重构信号的模糊熵值FE,取min{FE}所对应的α作为最优惩罚因子用于信号的VMD分解。 步骤3 计算各IMF分量的能量熵增量Δqi和频域互相关系数ρf,通过判定阈值确定虚假模态和噪声干扰成分,得到初步去噪信号x′(t)。 步骤4 针对含有高频噪声干扰的IMF分量采用MODWPT方法其进行去噪处理,进一步提升去噪效果和性能指标。 步骤5 将MODWPT去噪的IMF分量和表征信号特征的各敏感模态分量进行重构,形成去噪信号x″(t)。 该方法的计算流程如图8所示。 图8 算法流程图 为验证本文所提方法的有效性,对实际采集到的齿轮断齿故障信号进行去噪处理与分析。所采用试验平台为PQZZ-II型机械故障模拟综合试验台。断齿故障模拟时,将驱动齿轮的一齿折断,使折断线位于分度圆附近。 试验过程中,电动机转频为50 Hz,数据采集系统以ADA16-8/2(LPCI)型高速多功能采集卡为基础进行搭建,传感器采用KD1001L型压电式加速度传感器,为全面监测齿轮箱运行状态,加速度传感器布置在输出轴轴承X方向上。信号采集时,将采样频率设置为fs=5 120 Hz,采样时长15 s,分析时长1 s。齿轮箱中各齿轮均为标准直齿轮,其中,驱动齿轮和从动齿轮的齿数分别为55和75,齿轮材料为S45C,模数为2 mm,输入轴的平均转速为880 r/min。经计算,可得驱动齿轮的转频f1=14.67 Hz,从动齿轮转频f2=10.76 Hz,啮合频率fz=806.67 Hz。图9为该试验台的平面结构示意图。 1.三相交流变频电机;2.电机安装基座;3.电机位置调节螺栓;4.同步皮带轮;5.传动轴支座;6.联轴器;7.传动齿轮轴;8.轴承压盖;9.齿轮箱;10.联轴器;11.磁粉扭力器;12.试验平台底座;13.轴系平台位置调节螺栓;14.轴承更换端轴承座;15.轴系平衡定位销;16.轴系平台紧固螺栓;17.百分表;18.旋转圆盘;19.旋转轴;20.轴系平台;21.轴承座;22.刚性联轴器;23.电机底板紧固螺栓;24.轴承座紧固螺栓。 试验采集到的齿轮断齿故障振动信号的时域波形如图10(a)所示。对于齿轮故障的诊断,包络谱分析是最为常用的方法[22],因此,为诊断出齿轮故障类型,求解齿轮故障信号的包络谱,并示于图10(b)。 由图10可知,由于信号采集系统中未采用相应消噪装置,致使采集到的时域信号中含有较多噪声成分;由于噪声干扰成分的影响,该信号的包络谱中只在与驱动齿轮2倍转频相对应的29.38 Hz处出现较为明显的峰值,根据包络谱特性,仅可初步判定与输入轴相连的驱动齿轮存在故障,但齿轮的故障特征以及所属故障类型从中难以读取和判别。 图10 齿轮故障信号时域波形及其包络谱 按照本文所提VMD分解参数选择方法对预设尺度K和惩罚因子α进行选取,经计算K=4、α=2 100时,分解效果最佳。齿轮故障信号经VMD分解后各IMF分量及其频谱如图11所示。 由图11可知,VMD方法在一定程度上克服了EMD中存在的模态混叠问题,各IMF分量集中在各自中心频率附近,有效减少了各模态分量间的信息泄露。 图11 齿轮故障信号VMD分解结果及其频谱 为比较分解效果,采用EEMD方法对齿轮故障信号进行分解,得到12阶IMF分量,由于EEMD分解后的信号特征主要集中在前几阶模态分量[9],在此仅列出前4阶模态分量的时域波形和频谱,并示于图12。其中,EEMD分解时,所添加白噪声的标准差ε0=0.2,总体实验次数I=100。 图12 齿轮故障信号的EEMD分解结果 由图12可知,EEMD方法在一定程度上抑制了模态混叠问题,但仍可看出分解效果并不理想,尤其对于IMF1分量,在其整个频率范围内几乎都存在频率成分,且该方法都分解出了多阶迭代误差分量。这势必将影响后续信号故障特征提取的准确性与故障诊断的可靠性。 计算VMD分解得到各IMF分量的能量熵增量Δqi和频域互相关系数ρf的结果如图13所示。 由图13可以判定IMF2和IMF3为表征信号自身特征的敏感模态分量;IMF1为包含分解迭代误差和背景信号的干扰分量;IMF4为高频噪声干扰成分。 图13 VMD分解所得各IMF分量能量熵增量和频域互相关系数 为有效提升去噪效果和性能指标,采用MODWPT对包含高频噪声干扰成分的IMF4进行分解,分解过程中选择长度L=22的Fejer-Korovkin小波滤波器,分解层数J=4,分解所得低频分量如图14所示。 图14 高频噪声分量IMF4的MODWPT分解结果 由图14可知,高频噪声分量IMF4经MODWPT分解后,其频率最低分量C1中的噪声干扰成分得到有效滤除,信号自身特征较为明显。将其作为高频去噪分量与VMD分解所得表征信号自身特征的主模态IMF2和IMF3分量进行重构,重构后去噪信号的时域波形和包络谱如图15所示。 图15 重构后去噪信号的时域波形及包络谱 由图15(a)可知,本文所提方法有效滤除了原信号内绝大多数无用的低频干扰和高频噪声成分,齿轮故障信号得到有效提纯;同时分析图15(b)的包络谱图可以发现在14.71 Hz、20.63 Hz、29.38 Hz、44.15 Hz、53.84 Hz、58.75 Hz、66.31 Hz和73.13 Hz出现明显峰值,这些峰值频率分别对应着驱动齿轮的1倍~5倍转频f1以及从动齿轮的2倍频、5倍频和6倍转频f2,而其它频率区域峰值较低。 根据齿轮故障诊断原理[23]以及齿轮断齿故障包络谱特征[22]可知:当齿轮发生断齿故障时,在啮合过程中会激发瞬时冲击缺陷,致使断齿故障信号具有丰富的频域特征。断齿故障的包络谱中除包含故障齿轮的转频fr及其整数倍频外,同时还会有与其相啮合齿轮的高倍转频的出现。根据上述原理并结合图15(b)可诊断出与输入轴相连的驱动齿轮存在断齿故障。 为说明本文所提方法的有效性和优越性,采用EEMD的小波阈值信号去噪方法对齿轮故障信号进行去噪处理,去噪结果如图16所示。其中,小波阈值处理信号时采用db5小波基和“Heursure”规则进行软阈值降噪。 图16 EEMD小波阈值去噪后齿轮故障信号及其包络谱 由图16可知,基于EEMD小波阈值信号去噪方法的去噪效果并不理想,去噪后信号中仍有大量噪声成分残留。而其包络谱中,虽能识别出驱动齿轮的转频及其部分整数倍频,但与其相啮合齿轮的高倍转频成分的谱线并不明显,从中无法准确判别齿轮的故障类型;同时,由于低频背景信号和迭代误差等虚假成分并未得到有效滤除,去噪信号包络谱的低频区域存在较多虚假频率成分,这也进一步增加了信号故障类型诊断的难度。 本文提出一种基于VMD和MODWPT的信号去噪方法,并将其应用于齿轮故障特征提取中,通过对仿真信号和实测数据的分析,验证了所提方法的有效性和实用性,结论如下: (1)基于效中心频率数量N和模糊熵最小原则的VMD分解参数选择算法,可有效提升信号分解效果,抑制模态混叠现象的产生。 (2)基于能量熵增量-频域互相关系数准则的敏感模态分量选取算法,能够有效滤除信号中的分解误差和背景信号等虚假成分,并由MODWPT方法对含有高频噪声的模态分量进行分解去噪后,可进一步提升信号的去噪效果。 (3)相较于EEMD小波阈值去噪方法,本文所提方法解决了去噪过程中信号故障信息丢失的问题,并抑制了由于模态混叠而造成信号内噪声无法完全滤除的现象,通过仿真信号和实测齿轮断齿故障信号的分析,证明了所提方法的有效性。


2.2 仿真信号分析


3 基于VMD-MODWPT的信号去噪方法

4 实测信号分析







5 结 论
