非一致地震激励下大跨度桥梁弹塑性随机响应分析研究
2021-06-30刘小璐
刘小璐, 苏 成, 聂 铭
(1. 广东电网有限责任公司电力科学研究院, 广州 510080; 2. 华南理工大学 土木与交通学院, 广州 510640)
大跨度桥梁不同支承处的地震激励存在显著的非一致性,主要表现为行波效应、失相干效应和局部场地效应,分别反映各支承处地震激励间的相位差、相干性损失和频谱差异[1]。同时,地震动具有本质上的随机性,应该采用随机振动方法对大跨度桥梁结构开展非一致地震响应分析研究。国内外学者已采用不同随机振动方法开展了大跨度桥梁非一致地震激励问题研究。例如,Allam和Datta[2]与Dumanogluid和Soyluk[3]采用功率谱法计算了非一致地震激励下大跨度斜拉桥的平稳随机响应;Lin等[4]、焦常科和李爱群[5]与赵雷和刘宁国[6]均采用虚拟激励法对非一致地震激励下的大跨度斜拉桥开展随机振动分析研究;刘小璐等[7]采用时域显式法研究了非一致地震激励下大跨度悬索桥的非平稳随机响应。
上述研究主要解决非一致地震激励下的线性随机振动问题。强震作用下桥梁局部构件会进入弹塑性状态,此时应该采用非线性随机振动方法进行抗震分析。国内外学者发展了多种非线性随机振动方法,如FPK方程法[8]、随机平均法[9]、矩方程法[10]、等效线性化法[11-12]、等效非线性系统法[13]、概率密度演化法[14]和Wiener路径积分法[15]等。其中,大部分方法仅限于解决小规模非线性问题,难以应用于大跨度桥梁结构[16]。等效线性化法因其较强的适用性在实际工程中得到广泛的应用,例如Colangelo[17]利用等效线性化法计算了多层弹塑性框架在一致平稳地震激励下的随机响应;赵岩等[18]采用虚拟激励法求解非线性结构的等效线性化运动方程,计算了连续梁桥在一致平稳地震激励下的弹塑性随机响应。尽管如此,该方法在求解非平稳随机问题时需要在不同时刻建立一系列等效线性系统,对于大规模工程结构来说,计算量较大。该方法一般只能获取结构响应的一、二统计矩,无法直接获取非线性结构响应的尾部概率分布和峰值等更全面的统计信息。此外,随机模拟法[19]是一种原理简单且通用性强的方法,可以准确获取非线性结构随机响应的任意阶统计矩及概率分布,经常用来检验其它方法的计算精度。但随机模拟法需涉及到大量反复的确定性样本分析,若采用传统弹塑性时程分析法进行样本分析将会非常耗时。
在作者前期研究[20]基础上,针对非一致地震激励下局部进入弹塑性状态的大跨度桥梁结构,基于大质量法[21]提出了一种时域显式降维迭代算法,可以快速进行非一致地震激励下的弹塑性时程分析。将该方法与蒙特卡罗法结合,提出了一种时域显式降维迭代-随机模拟法,可高效获取非一致地震激励下大跨度桥梁结构弹塑性响应的统计矩和平均峰值。以主跨为1 200 m的某大跨度悬索桥为工程算例,采用纤维梁柱单元模拟大桥弹塑性构件,开展非一致地震激励下弹塑性随机振动分析研究,考察地震动空间效应对弹塑性随机响应的影响。
1 非一致地震激励
考虑地面运动加速度为均匀调制的非平稳零均值随机过程,则结构支承处的非一致地面运动加速度向量可表示为
X(t)=Ψ(t)x(t)
(1)
式中
(2)
式中:m为非一致地震激励个数;Xj(t)(j=1,2,…,m)为第j个非平稳地面运动加速度;ψj(t)为反映Xj(t)非平稳特性的均匀调制函数;xj(t)为Xj(t)的平稳部分,它们的互功率谱矩阵Sx(ω)可表达为
(3)
式中:Sjj(ω)为xj(t)的自功率谱,Sjk(ω)(j≠k)为xj(t)与xk(t)间的互功率谱。
根据式(3)所示的功率谱矩阵,采用谐波合成法生成非一致非平稳地面运动加速度为

(j=1,2,…,m)
(4)
式中:N为频率分量个数;ωi为第i个频率分量的圆频率;φki为在(0,2π)范围内均匀分布的随机相位角,且当k≠r或i≠s时,φki和φrs相互独立;ajk和θjk分别为第j与第k个地面运动加速度间的相关幅值与相关相位角。
对平稳地面运动加速度x(t)的互功率谱矩阵Sx(ω)进行Cholesky分解,可得
Sx(ω)=B(ω)B*T(ω)
(5)
式中
(6)
则式(4)中的ajk(ω)和θjk(ω)可分别表示为
(7)
(8)
式中:Δω为圆频率间隔,函数Im、Re分别表示取复数的虚部、实部。
2 大质量法
在一致地震激励下,结构内力只与结构相对地面的位移有关,因此一般基于结构相对位移建立运动方程,其中地震激励为结构各质点上一致的地面运动加速度。而在非一致地震激励下,无法建立唯一的结构-地面相对坐标系,因此结构运动方程及其地震激励施加方式与一致地震激励情况大为不同。常用的处理方法有相对运动法和大质量法,其中相对运动法由于需要进行叠加运算不适用于非线性情况,而大质量法没有这方面的限制,具有更强的适用性。
大质量法是对结构模型进行动力等效的一种分析方法,该方法在处理非一致地震激励问题时需要解除支承点沿地震作用方向的约束,并赋予该支承点大质量,此时弹塑性结构的运动方程可写为
(9)
式中
(10)
(11)
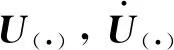
3 时域显式降维迭代法
对于局部弹塑性结构,将结构非线性恢复力向量F(U)分解为线性部分和仅与弹塑性单元恢复力相关的部分为
F(U)=K0U+LnFn
(12)
式中:K0为结构初始弹性刚度阵;Ln为弹塑性单元恢复力的指示矩阵;Fn为弹塑性单元恢复力中的非线性部分可表示为
Fn=R(Un)-Kn,0Un
(13)
式中:R为弹塑性单元的恢复力向量;Un为弹塑性单元的节点位移向量;Kn,0为弹塑性单元的初始弹性刚度矩阵,属于结构初始弹性刚度矩阵K0的一部分。将式(12)代入式(9),并将非线性部分移至方程右端,可得
(14)
式中
(15)
L=[Lx-Ln]
(16)
Vi=Ai,0P0+Ai,1P1+…+Ai,iPi
(i=1,2,…,nt)
(17)
式中:Vi=V(ti),Pi=P(ti),i=1,2,…,nt,其中nt为总时间步数;Ai,j(j=0,1,…,i)为系数矩阵,它们只与结构参数有关,可表达为如下闭合公式:
(18)
基于Newmark-β积分方法可获取T,Q1和Q2为
(19)
式中:I为单位矩阵;取γ=0.5,β=0.25,则Newmark-β积分方法可以实现无条件稳定。
对于当前时刻ti,假设已逐步计算出结构响应V0,V1,…,Vi-1,则式(17)右端的为已知量P0,P1,…,Pi-1,然而P1中依然含有关于未知向量Un,i的非线性项,需要进行迭代计算。式(17)共有2nd(nd为结构总自由度数)维,对于大规模结构,直接迭代求解该式的计算量较大。为了提高计算效率,从式(17)中提取Un,i相关的行,可得

(20)

Ψ(Un,i)=Yi(i=1,2,…,nt)
(21)
式中
(22)
(i=1,2,…,nt)
(23)
采用Newton-Raphson方法求解式(21),将所获得的收敛结果Un,i代入式(17)的其余行中,则得到结构当前时刻其它单元的节点位移向量。例如对于结构某一关键响应r,可表示为
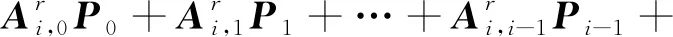
(24)

4 时域显式降维迭代-随机模拟法
将时域显式降维迭代法与蒙特卡罗法相结合,利用时域显式降维迭代法进行样本分析,高效获取非一致地震激励下大跨度桥梁结构的弹塑性随机响应,具体计算步骤如下:
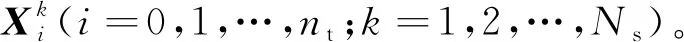
(2)建立结构初始有限元模型,释放地震激励方向的支承约束,并在相应自由度施加大质量。

5 工程实例
5.1 有限元模型
虎门二桥大沙水道桥是一座主跨1 200 m的地锚式悬索结构。该桥跨径布置为(360+1 200+480)m,矢跨比1∶9.5,如图 1所示。门式塔高191.1 m,设上、下两道横梁,如图2所示。主塔为钢筋混凝土结构,塔底截面及其配筋情况如图 3所示,其中纵向受力钢筋强度等级为HRB400,混凝土强度等级为C50。利用ANSYS建立大桥的初始三维有限元模型。其中,主梁、主塔和边墩均采用梁单元模拟,主缆和吊杆则通过杆单元模拟。主塔和边墩底部固支,主缆通过大桥的两侧锚碇固定。主梁侧向和竖向运动受主塔和边墩的约束,而纵向运动不受主塔和边墩约束。

图1 悬索桥立面图
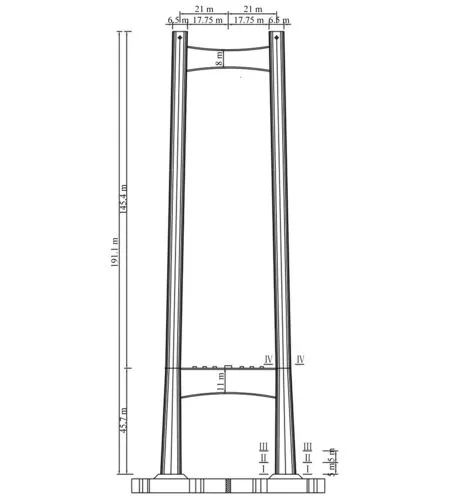
图2 主塔立面图

图3 主塔塔底截面及其配筋图
历史震害数据表明,大跨度悬索桥主塔相对其它部位更容易损伤[22]。虎门二桥大沙水道桥抗震专题研究表明,在重现期分别为945年和2450年的中震和大震作用下,整个结构可以依然处于弹性状态,然而主塔塔底截面承载能力的冗余度远低于其它关键截面。因此,当发生强度高于大震的地震时,主塔塔底截面可能会率先进入弹塑性状态,应该采用弹塑性单元模拟主塔底部,并预设塑性发展范围为塔底10 m以内,在后续分析中将对该塑性发展范围进行验证。在地震和恒载作用下,主塔底部主要受到轴力、剪力和弯矩作用,由于不允许发生剪切破坏,在此仅考虑轴力和弯矩引起的塑性行为,并采用可以模拟轴力-弯矩耦合作用的纤维弹塑性单元对预设的塔底塑性范围进行模拟。分别采用Menegotto-Pinto模型[23]和修正Kent-Park模型[24]模拟钢筋纤维和混凝土纤维的轴向应力应变关系,钢筋的屈服强度和混凝土的抗压强度分别取为330 MPa和22.4 MPa。本文通过几何非线性静力分析计算恒载引起的大位移和应力刚化效应,在此基础上开展地震激励下的结构动力分析,不考虑地震激励新引起的几何非线性效应。
5.2 非一致地震激励
考虑东、西塔底地震激励的差异性,而同侧塔底与锚碇相距较近,因此可以认为同侧塔底与锚碇的地震激励具有一致性。为此,该结构共有2个非一致地震激励,式(1)中反映地面运动加速度非平稳的均匀调制函数可表示为
(25)
式中:ta=3.2 s,tb=17.0 s,c=0.13。地震激励间的互功率谱可表示为
(26)

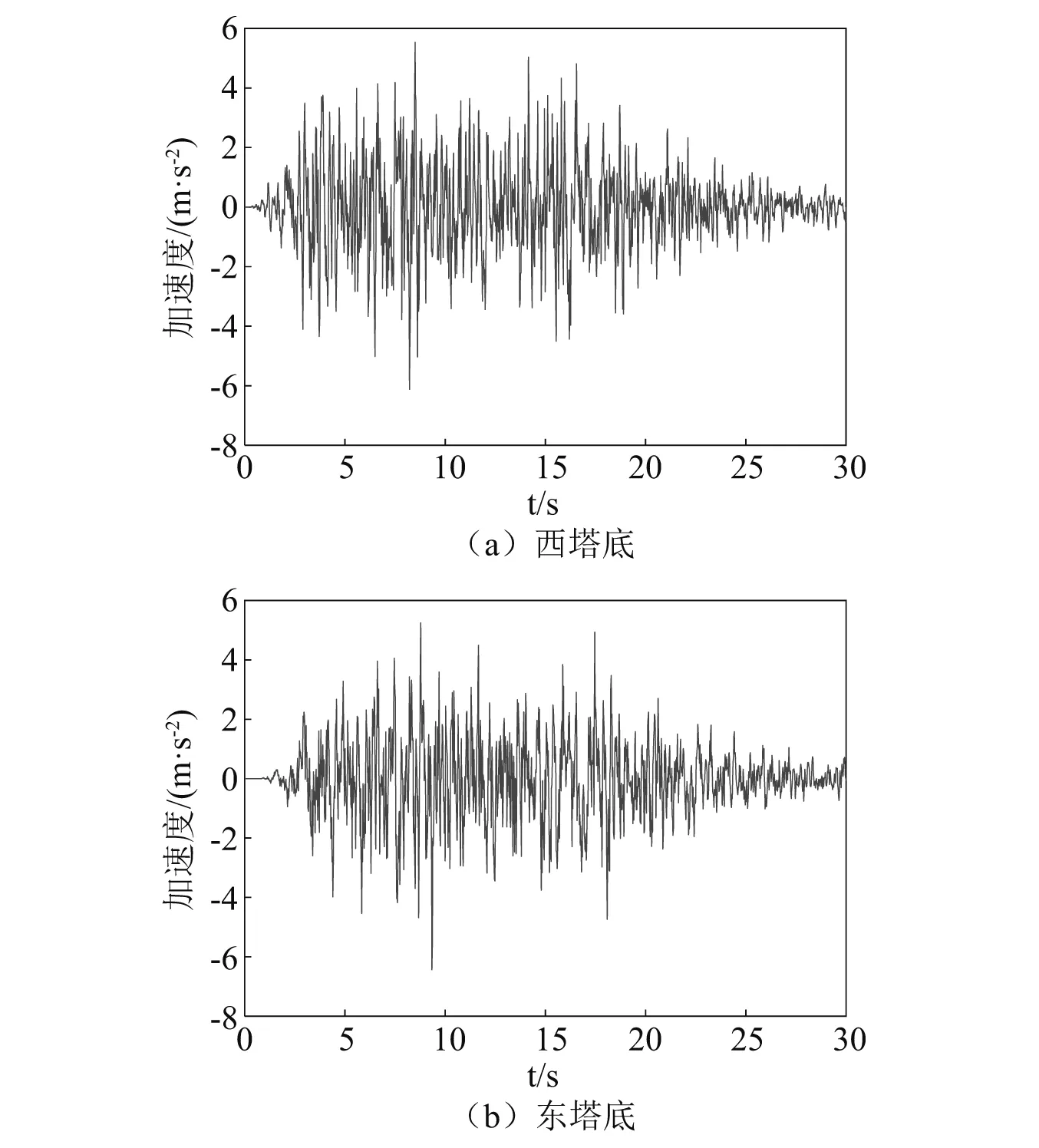
图4 非一致地面运动加速度时程样本
5.3 弹塑性时程分析
针对图 4所示的非一致地面运动加速度时程样本,分别采用本文的时域显式降维迭代法和传统非线性Newmark-β法对大桥进行弹塑性时程分析。东塔底部截面Ⅰ和下横梁上截面Ⅳ的弯矩时程分别如图 5和图 6所示。从图中可以看出,两种方法的结果完全重合,验证了时域显式降维迭代法的准确性。

图5 东塔截面Ⅰ的弯矩时程
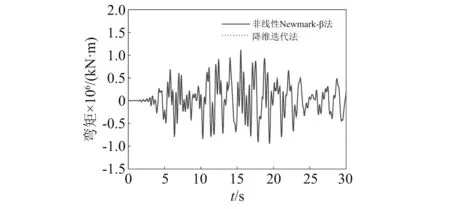
图6 东塔截面Ⅳ的弯矩时程
传统非线性Newmark-β法和时域显式降维迭代法的计算时间分别为2 518.3 s和127.4 s。显而易见,本文的时域显式降维迭代法具有更高的计算效率,这是因为该方法仅仅需要对主塔底部4个弹塑性纤维单元进行非线性降维迭代运算,而传统方法需要将桥梁所有自由度捆绑一起进行迭代计算。需要指出的是,本文方法的计算时间主要包括两部分:一部分用于构建如式(17)所示动力响应显式表达式中的系数矩阵,为109.9 s;另一部分用于降维迭代运算,仅为17.5 s。其中,系数矩阵只依赖于结构本身信息,它们只需要计算一次,随后可重复用于后续随机模拟的所有样本分析中。
为了考察强震作用下主塔塑性变形的发展情况,给出如图 2所示东塔底部截面Ⅰ-Ⅲ的弯矩-曲率关系,分别如图7(a)~(c)所示。从图中可看出,非一致地震激励下截面Ⅰ的弯矩-曲率曲线呈现出相对饱满的旗形滞回环,表明截面Ⅰ表现出显著的弹塑性行为;截面Ⅱ的滞回环面积明显减小,非线性行为相对较弱;而截面Ⅲ的弯矩-曲率关系几乎趋近于线弹性。以上结果表明,长度为10 m的弹塑性纤维单元可以完全捕捉主塔底部的弹塑性变形行为。截面Ⅰ-Ⅲ最外侧钢筋应力-应变关系如图8(a)~(c)所示,同样表明在所关注的地震水准下,主塔底部弹塑性行为发展未超出预期范围。

图7 东塔底部截面Ⅰ-Ⅲ的弯矩-曲率关系

图8 东塔底部截面Ⅰ-Ⅲ外侧钢筋应力-应变关系
5.4 弹塑性随机振动分析
时域显式降维迭代法用于弹塑性时程分析的计算精度和计算效率均得到了验证,可进一步利用时域显式降维迭代-随机模拟法开展弹塑性抗震随机振动分析。为了考察地震激励非一致性的影响,同时计算悬索桥在一致和非一致顺桥向地震激励下的弹塑性随机响应,其中非一致地震激励按5.2节中的参数确定,一致地震激励取其东塔底处的激励,随机模拟样本数取为500。
两种地震激励工况下西塔和东塔底部截面内力标准差分别如图9和图10所示。从图中可以观察到,对于西塔底截面,非一致地震激励下的轴力标准差偏小,而剪力和弯矩标准差偏大;对于东塔底截面,非一致地震激励下的轴力和弯矩标准差偏小,剪力标准差与一致地震激励下的结果非常接近。由此可知,地震激励空间效应会使得该大跨度悬索桥内力结果既可能偏大也可能偏小。

图9 西塔底截面内力标准差
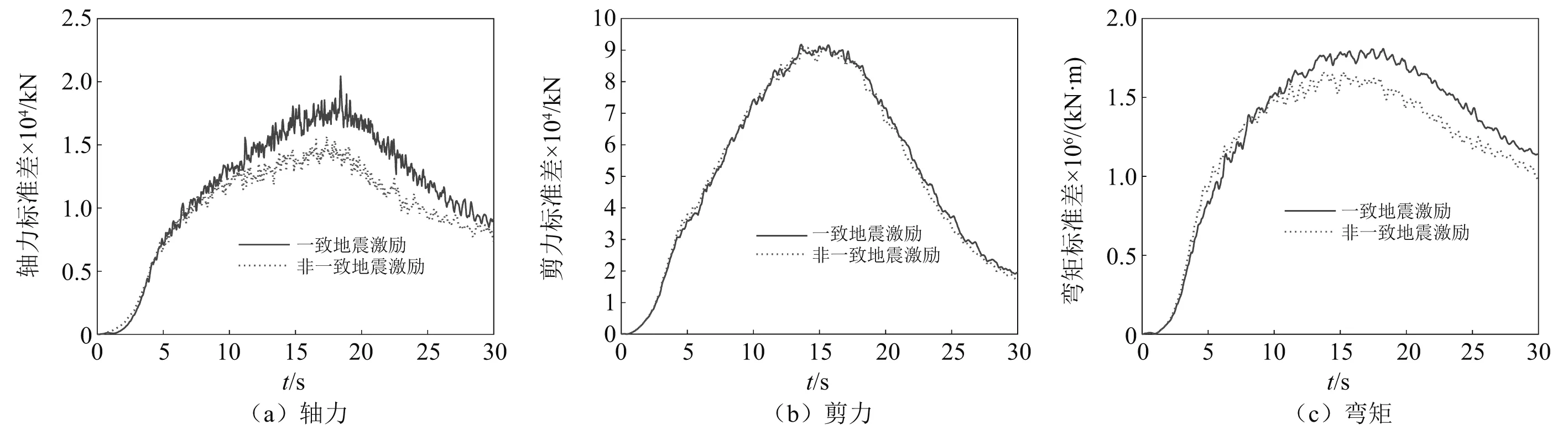
图10 东塔底截面内力标准差
此外,利用本文方法可进一步获取大桥关键响应的平均峰值。主塔底截面轴力、剪力和弯矩的平均峰值如表1所示。为了考察地震激励空间效应对结构响应的影响,将两种工况的相对差异也列于表1中。从表中可以看出,地震激励空间效应对响应平均峰值的影响规律与对响应标准差的影响规律基本相同。值得注意的是,当考虑地震激励空间效应时,东塔底截面轴力的平均峰值比一致地震激励下的结果小了9.4%;西塔底截面剪力和弯矩的平均峰值比一致地震激励下的结果分别大了12.4%和11.8%。在该大桥弹塑性抗震设计中需要考虑地震激励空间效应对结构内力的影响。

表1 塔底截面内力的平均峰值
时域显式降维迭代-随机模拟的计算时间如表2所示,取不同样本数,平均每个样本分析的时间基本相同,均是13 s左右。这表示只需要花13 s的时间就可以完成一次大跨度悬索桥确定性弹塑性时程分析。当样本数为500时,时域显式降维迭代-随机模拟法的计算时间为不到2个小时,而基于传统非线性Newmark-β方法的随机模拟法的计算时间则接近200个小时。本文的时域显式降维迭代-随机模拟法在计算效率方面具有明显的优越性。以上所有的计算均是在带有Intel Core i5处理器和4 GB内存的台式机上完成的。

表2 时域显式降维迭代-随机模拟的计算时间
6 结 论
(1)基于大质量法推导了非一致地震激励下结构动力响应形式上的时域显式表达式,利用该显式表达式的降维列式优势,提出仅关于弹塑性单元节点自由度的时域显式降维迭代算法,显著提高非一致地震激励下大跨度桥梁弹塑性时程分析的计算效率。并结合蒙特卡罗法,提出了非一致地震激励下大跨度桥梁弹塑性随机振动分析的时域显式降维迭代-随机模拟法。
(2)以虎门二桥大沙水道桥为工程实例,开展顺桥向非一致地震激励下的弹塑性随机振动分析,验证了本文方法的正确性和高效性。研究结果表明,对于该大跨度悬索桥,非一致地震激励下主塔内力的标准差和平均峰值比一致地震激励下的结果既可能偏大也可能偏小,其中东塔底截面轴力的平均峰值偏小了9.4%,西塔底截面的剪力和弯矩平均峰值分别偏大了12.4%和11.8%。在该大桥弹塑性抗震设计中需要考虑地震激励空间效应对结构内力的影响。
