基于复包络谱的滚动轴承故障特征提取方法研究

黄传金， 宋海军， 秦 娜， 雷文平， 孙熙庆， 柴 鹏

(1.郑州工程技术学院 机电与车辆工程学院, 郑州 450044； 2.西南交通大学 电气工程学院, 成都 610031 3.郑州大学 机械工程学院, 郑州 450052)

滚动轴承是工业旋转机械重要部件，通过振动信号监测轴承状态是常用的方法。从振动信号中提取故障激发的固有振动信号是故障特征提取的关键环节[1-2]。滚动轴承故障引起的振动信号是非平稳信号，一些先进的数字信号处理方法被用于诊断滚动轴承故障，如运用小波变换(wavelet transform，WT)[3]、经验模态分解(empirical mode decomposition，EMD)、局部均值分解(local mean decomposition ，LMD)等先进数字信号处理方法将滚动轴承振动信号分解成不同频带的信号[4-7]，然后结合包络解调提取故障激发的固有振动频率。

滚动轴承工作环境复杂，故障类型多样，不同的位置发生故障，不同方向的振动信号强度和频谱结构也不尽相同，Chen等[8]指出仅根据单个方向振动信号特征监测故障状态可能引起误判和漏判；程军圣等[9]遇到过根据单个通道的信号无法解调出滚动轴承外圈故障的案例。

随着传感器技术的发展，二维、三维传感器已经比较普遍，在转子故障诊断中，通常采集位移信号，根据稳态时正交位移信号回转特性，Benlty公司提出了全频谱[10]，Qu等[11]提出了全息谱，韩捷等[12]提出了全矢谱。较之单通道信号，上述同源信息融合技术包含了更多传感器振动信号，可以获得质量更高的信息。为处理非平稳信号，文献[13-14]分别提出与EMD、LMD相结合的同源信息融合技术。因为基于EMD、LMD的数据驱动分解方法不能保证有相同的分解尺度，即不同通道的信号分解出的固有模态函数个数不一致，给后续的信息融合带来困难；为保证每个通道信号具有相同的分解尺度，文献[15]提出多元经验模态分解(multivariate empirical mode decomposition，MEMD)和全频谱相结合旋转机械故障诊断方法；文献[16]提出基于二元经验模态分解(bivariate empirical mode decomposition，BEMD)的全矢包络谱技术诊断高温余热发电机组故障；文献[17]联合复局部均值分解(complex local mean decomposition，CLMD)和全矢谱提取转子故障特征，做出的诊断结果更为准确。同源信息融合技术与多元的数据驱动分解方法相结合，确保了信号有相同分解尺度。

在转子故障监测中，通过正交的位移传感器采集的振动信号可以组成一个椭圆形式的回转轨迹，通过全矢谱技术可以获取椭圆长轴、短轴等信息，而滚动轴承故障特征包含在高频信号中，需要用加速度传感器采集振动信号，加速度信号已不具有转子回转特性的物理意义，如何融合正交方向的信号特征需要进一步的探讨。

考虑复傅里叶变换具有增强复数信号幅值和融合复数信号频率的特性；较之全矢谱，复傅里叶变换运算更为简单、快速，而且复傅里叶变换获取的特征频率更加显著。本文提出了一种基于复包络谱的滚动轴承故障特征提取方法，将正交采样获取垂直方向的振动信号组成一个复数，然后运用BEMD将复数分解成系列复固有模态函数(complex intrinsic mode function，CIMF)，用Hilbert变换分别对CIMF的实部和虚部进行解调得到各自的包络信号，组成一个复包络信号，最后运用复傅里叶谱融合两个方向的振动信号特征。所提方法既可加强微弱振动信号特征，进行早期故障特征提取，也可综合两个方向的振动信号的频率特征，提取的信息更为全面、准确。

1 复傅里叶变换及其与全矢谱的比较

1.1 复傅里叶变换原理

对一个复数ai(t)=axi(t)+jayi(t)，其快速傅里叶变换(fast foureir transform，FFT)为Ai(jω)，根据FFT线性性质有：

(1)

在笛卡尔坐标系中，有：

Axi(jω)=Re[Axi(jω)]+jIm[Axi(jω]

(2)

(3)

根据傅里叶变换的共轭对称性，有：

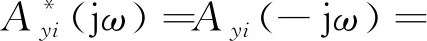
(4)

则有：

Ai(jω)={Re[Axi(jω)]+Re[Ayi(jω)]}+
j{Im[Axi(jω)-Im[Ayi(jω)]}

(5)

通过式(5)可知，复数信号ai(t)实部和虚部中频率相同的谐波，其傅里叶变换结果的实部等于实部信号axi(t)和虚部信号ayi(t)的FFT中实部信号的之和，虚部为二者虚部信号之差；当ai(t)实部和虚部中含有频率不同的谐波时，其FFT结果可以综合axi(t)和ayi(t)中的频率特征。故复信号的FFT具有增强特征幅值和频率综合的能力，举例说明。假设复数信号数学表达式如下：

zi(t)=Axicos 2πfxit+jAyisin 2πfyit,i=1,2,3,4

(6)

考虑四种情况：①同频同幅值，即：Ax1=Ay1=0.3，fx1=fy1=50 Hz；②同频、实部幅值大于虚部的，即：fx2=fy2=50 Hz，Ax2=0.3，Ay2=0.2；③同频、实部幅值小于虚部的，即：fx3=fy3=50 Hz，Ax3=0.2，Ay3=0.3；④不同频、实部幅值小于虚部的，即：fx4=50 Hz，fy4=25 Hz，Ax4=0.2，Ay4=0.3。假设采样频率Fs=200 Hz，序列长度为4 096，则复傅里叶变换以及实部和虚部的傅里叶变换，如图1所示。

从图1中第一种情况可知，当同频同幅时，特征频率幅值等于实部和虚部的幅值之和；从第二种、第三种情形可知，当同频幅值不同时，出现两个频率关于Fs/2对称(称为对称特征频率)，第一个频率幅值为实部和虚部幅值之和，第二个频率幅值为二者之差，通过第二个频率的正负可比较实部和虚部幅值大小；从第四种情况可知，当即不同频也不同幅时，复傅里叶谱可综合实部和虚部的频率特征信息。

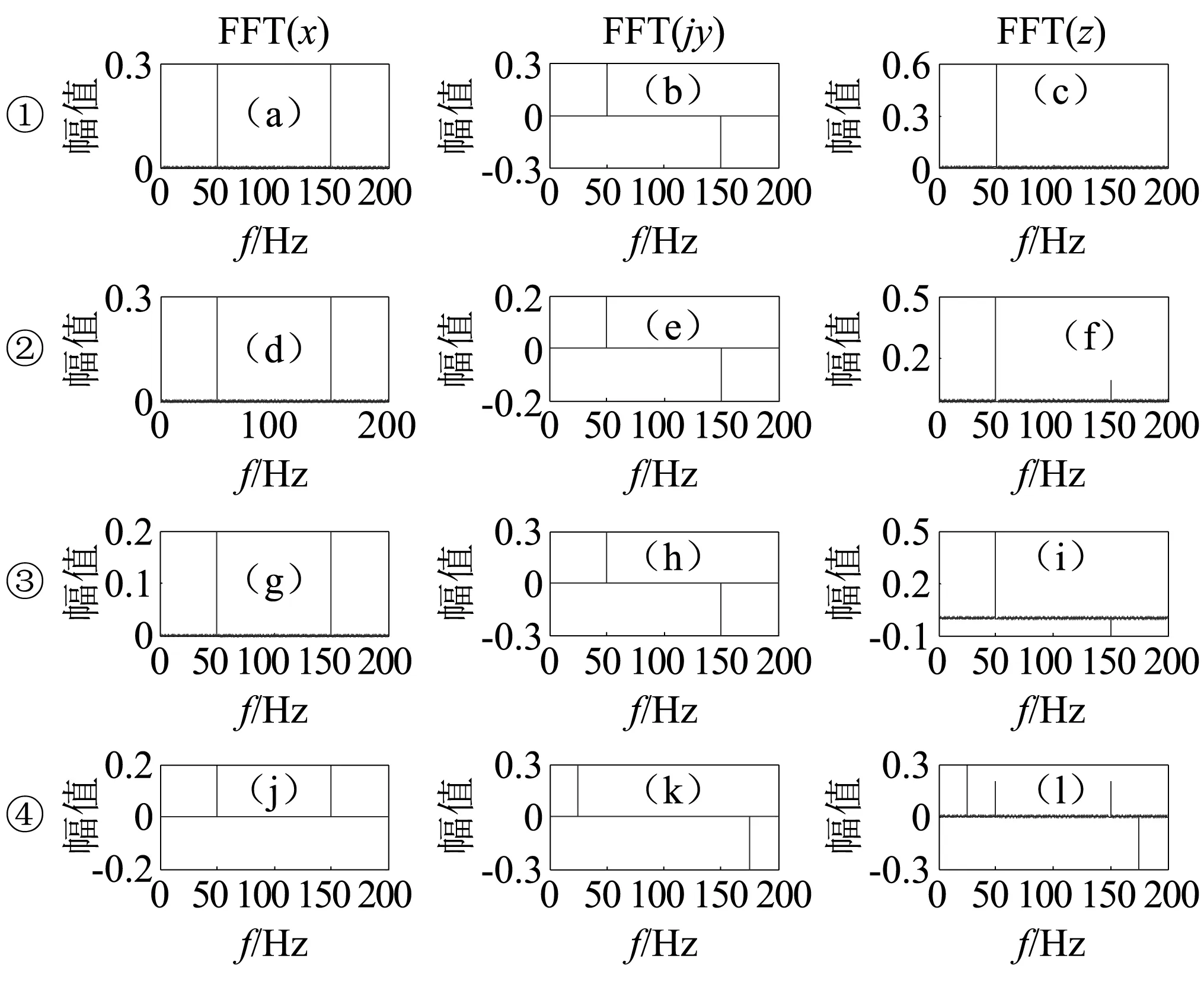
图1 四种情况的复傅里叶变换以及实部和虚部的傅里叶变换结果

1.2 复傅里叶变换和全矢谱的对比分析

因为复序列z(k)的傅里叶变换的幅值和|z(k)|有关，如果用三角函数表示，可以发现|z(k)|和x、y的初相位有关。为便于分析，令x(t)=A1cos2 πft，y(t)=A2×cos(2πft+φ)，其中f=50 Hz，φ=(k/8)π(k=±1,±2,…,±16)，采样频率Fs=800 Hz。研究以下三种组合时初相位φ变化时复傅里叶谱和全矢谱的联系与区别；①A1=A2=1；②A1=1；A2=0.5；③A1=0.5；A2=1。

第①情况对应的傅里叶谱和全矢谱如图2所示，第②和③二者结果相同，所得图如图3所示。从图2可知：①当y和x的相位相差0或π时，全矢谱方法和复傅里叶谱方法所得的幅值相同；②较之全矢谱方法，当φ∈(0，π)时，复信号的傅里叶谱中对称特征频率Fs-f幅值较大，在φ=0.5 π时，幅值增加了1倍；当φ∈(π，2π)时，复傅里叶谱方法获取的特征频率f的幅值较大；在φ=1.5π时，幅值增加了1倍；图3中有类似的结论。因此本文根据相位差选择复信号的特征频率段以表征信号频率。

图2 复信号的傅里叶谱和全矢谱的对比图(情况①)

图3 复信号的傅里叶谱和全矢谱的对比图(情况②、③)

2 基于复包络谱的滚动轴承故障诊断

所提的基于复信号包络谱的故障诊断实现方法如下：

(1)初始化。设置BEMD分解层数，BEMD算法详见文献[16]，本文取6；根据滚动轴承参数和电机转速，计算理论上的故障特征频率；因为轴承打滑等原因，实际中的特征频率和理论上的故障特征频率有误差，设置频率容差。

(2)用加速度传感器同过正交采样方式方法获取垂直方向上的加速度信号x、y，然后令z=x+jy，得到一个复数形式的二元信号。

(3)用BEMD将复信号z分解成系列CIMF，并将分解过程中得到前几阶CIMFi的实部包络信号aix和虚部包络aiy组成复数形式的包络信号ai=aix+jaiy(i=1,2,3)。

(4)对复信号ai做傅里叶变换。

(5)用傅里叶变换求取aix和aiy的初相位，计算aix与aiy的相位差φ；因为计算相位时用到除法，计算结果受噪声干扰较大，为此结合ai的傅里叶变换设定一个阀值λ，只计算abs[FFT(ai(k))]/N>λ时相位，以克服噪声干扰，本文取λ=0.05。

(6)依据φ的值到所在频率区间观察特征频率，并确定故障类型。

上述所述流程如图4所示。

图4 所提方法的流程图

3 算例分析

3.1 复合故障分析

3.1.1 试验介绍

试验设备采用SpectraQuest的旋转机械故障试验台MG2010，试验台在3/4英寸直径的TG铁轴上安装两个试验轴承，试验装置布局及缺陷轴承如图5所示。轴由1 HP三相异步电动机驱动，转速保持恒定在2 700 r/min，电机频率fn为45 Hz，电机端轴承是含有滚珠故障、内圈故障和外圈故障的复合故障轴承，型号为MB ER-12 K。分别将外圈故障设置在4 ∶30和9 ∶00方向来模拟不同的工况。两个三维加速度计分别安装在左右铝轴承壳体上，并与LMS SCADAS移动数据采集系统连接采集振动信号，采样频率为12.8 kHz。故障特征频率如表1所示。

图5 试验台布置示意图及复合故障轴承

表1 故障类型及其特征频率值

3.1.2 数据分析(外圈故障设置在4 ∶30方向)

将复合故障轴承中外圈故障设置在4 ∶30方向，测得的水平和垂直方向的振动信号x、y如图6所示。令z=x+jy，运用BEMD将z分解成系列CIMFs(分解层数为6)，分别运用Hilbert变换对第一阶CIMF1的实部和虚部信号进行解调，得到实部和虚部的包络信号a1x和a1y；然后令a1=a1x+ja1y，并直接对a1进行复傅里叶变换，则a1的复傅里叶变换结果以及全矢谱和相位谱如图7所示。由a1实部信号和虚部信号的相位差谱可知，由于其相位差在(0～π)之间，根据1.2节中复傅里叶变换和全矢谱的对比分析结论可知：a1的复傅里叶变换结果中对称特征频率处的幅值较大；因此，可采用对称特征频率处的幅值来表征振动强度。而且，对称特征频率处的幅值大于全矢谱中的特征频率处的幅值，如全矢谱中特征频率处长半轴的长度分别是fb为0.449、fo为0.141 9、2fb为0.294 7、fi为0.092 44、3fb为0.327 1；而复傅里叶变换对称特征频率处的幅值分别是fs-fb为0.629 5、fs-fo为0.154 3、fs-2fb为0.368、fs-fi为0.153 4、fs-3fb为0.383 6。

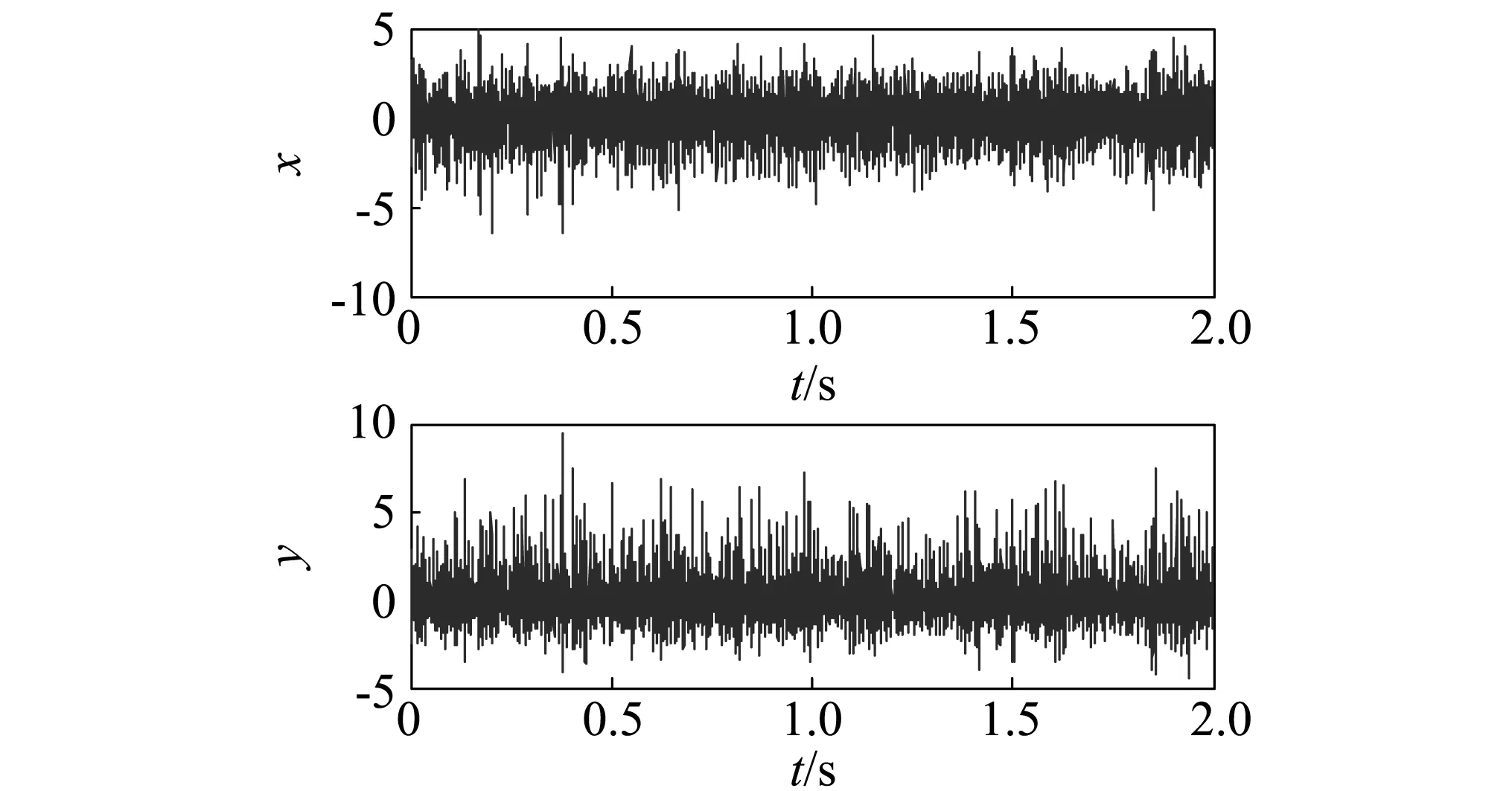
图6 外圈故障设置在4 ∶30时的振动信号x、y

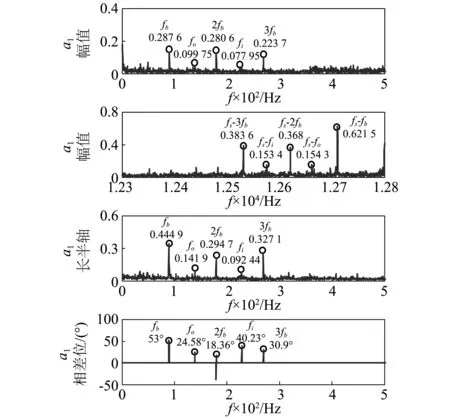
图7 a1的复傅里叶变换、全矢谱和相位差谱(外圈故障在4 ∶30方向)

3.1.3 数据分析(外圈故障设置在9 ∶00方向)

采用与3.1.2节同样的方法，获取的外圈故障设置在9 ∶00方向时的复傅里叶变换结果、全矢谱和相位差谱如图8所示。由图8中的相位差可知，特征频率处的相位差在(0～π)之间，复傅里叶变换中对称特征频率处的幅值较大；复傅里叶谱中滚动体故障对称特征频率fs-fb的幅值为0.881 1，而全矢谱中滚动体故障特征频率fb的幅值为0.569 3。

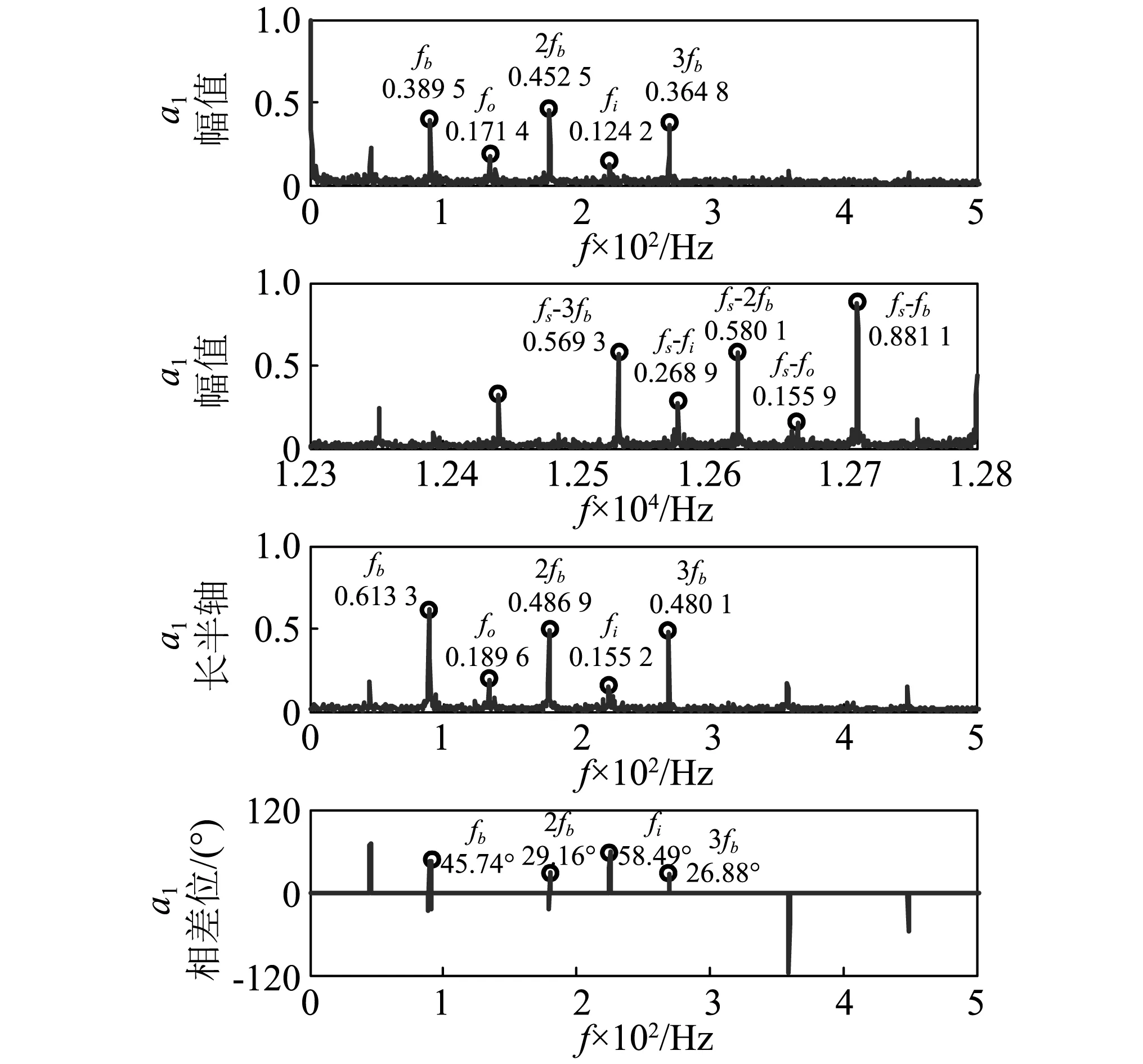
图8 a1的复傅里叶变换、全矢谱和相位差谱(外圈故障在9 ∶00方向)

3.2 XJTU-SY 滚动轴承复合故障分析

复合故障数据取自XJTU-SY 滚动轴承数据集40 Hz10 kNBearing3_22000.csv[18]，此时距试验失败结束还有496 min。试验中轴承型号为LDK UER204，转速为2 400 r/min，采样频率为25.6 kHz，采样时长为1.28 s，采样间隔为1 min，运行了41 h 36 min，共采集了2 496个文件，最后发生了内圈故障、滚动体故障、保持架和外圈复合故障，试验详情参见文献[18]。水平方向的信号x和垂直方向振动信号y的时域波形图，如图9所示。

图9 水平、垂直方向的振动信号x、y

令z=x+jy，然后运用本文所提方法获取的包络信号a2～a4的相位差、复傅里叶谱和全矢谱如图10所示(限于篇幅，省略了第一阶高频噪声信号)。从a2的相位差谱可知，实部和虚部信号的相位差为-122.5°，则a2的中外圈故障特征频率fo(125 Hz)的幅值较大，为0.100 2，外圈故障对称特征频率fs-fo的值为0.045 68，而全矢谱中的外圈故障特征频率fo的幅值为0.072 9，由此可知，根据本文方法得到的故障特征频率的幅值特征较大；图10中a3相位差在内圈故障特征频率fi-fn、fi和fi+fn处接近0或-π，则内圈故障特征、内圈故障特征对称频率和全矢谱中的特征频率幅值近似相等；图10a4的相位差在内圈故障特征频率fi(194 Hz)处为20.15°，则内圈故障对称特征频率fs-fi的幅值较大，为0.149，而全矢谱中内圈故障特征频率的幅值为0.136 1，进一步证明用本文所题方法获取的幅值特征更为明显。另外从图10明显可知轴承发生了外圈和内圈复合故障。

图10 a2-a4的相位差、复傅里叶谱和全矢谱

运用EMD分别将两个方向的振动信号分解成系列固有模态函数，然后用Hilbert变换解调获取相应的包络axi和ayi(i=1，2，3，4)，前4阶包络谱如图11所示。从图11可知，水平方向的振动信号有明显的外圈故障特征频率，内圈故障特征频率幅值较小；而垂直方向的振动信号有明显的内圈故障特征频率，而外圈故障特征较弱。分别运用快速谱峭度方法分析水平和垂直方向的振动信号x和y，相应的解调谱ax和ay如图12所示。由图12可知，通过快速谱峭度得到的包络谱含有明显的内圈故障特征，但外圈故障特征较弱。

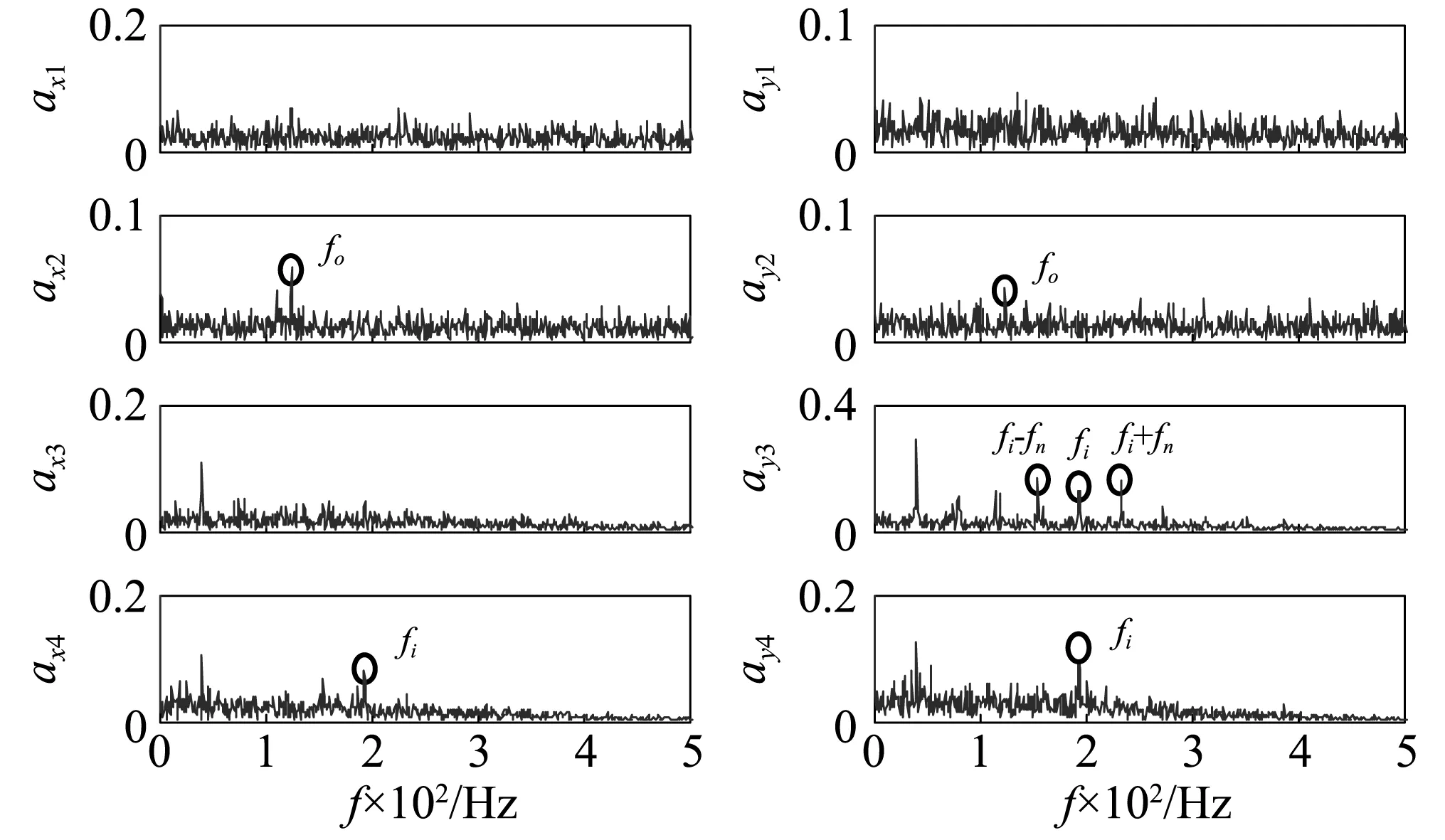
图11 基于EMD的包络谱axi和ayi(i=1，2，3，4)

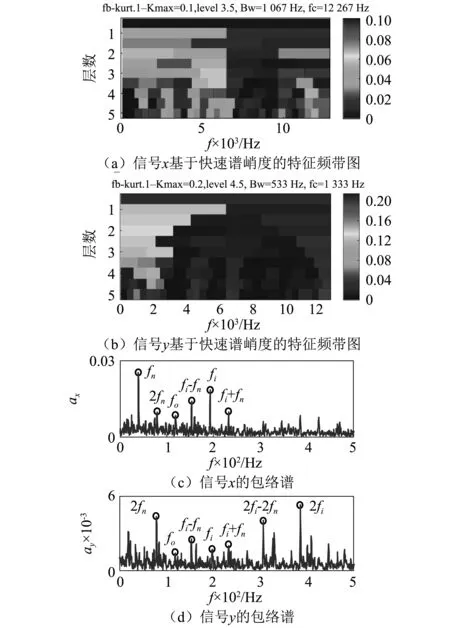
图12 快速谱峭度及其相应的包络谱

5 结 论

本文提出了一种基于复傅里叶变换的滚动轴承故障特征提取方法，融合了滚动轴承正交通道信号特征，增强了幅值并综合了频率。主要结论如下：

(1)当信号相位差接近于0°和π时，特征频率、对称特征频率和全矢谱的幅值近似相等；当相位差在(-π，0)时，复信号的傅里叶谱中特征频率幅值较大；当相位差在(0，π)时，复信号的傅里叶谱中对称特征频率幅值较大；

(2)复数形式的包络信号的傅里叶谱包含的故障特征更为丰富，不仅能增强故障特征的幅值信息，也可综合两个通道信号的频率特征。

滚动轴承复合故障类型多样，不同故障类型时，故障特征频率在CIMFs中的分布规律还需进一步研究。