基于深度森林的轴承故障诊断方法
2021-06-30丁家满吴晔辉罗青波
丁家满, 吴晔辉, 罗青波, 杜 奕
(1. 昆明理工大学 信息工程与自动化学院,昆明 650500;2. 昆明理工大学 城市学院,昆明 650051)
故障诊断方法可分为基于模型的方法、基于信号的方法、混合/主动方法和数据驱动方法[1]。其中,基于数据驱动方法通过收集大量的历史数据来建立故障诊断模型。近年来,海量故障数据[2]的收集也为数据驱动的故障诊断方法提供了新的机遇,并受到越来越多的研究者和工程师的重视。常用的故障诊断方法有:支持向量机(support vector machine,SVM),K近邻(k-nearest neighbor,KNN),人工神经网络(artificial neural network,ANN)等,诊断效果主要取决于故障特征能否准确地反映出故障类型的本质区别[3]。
对于海量数据的故障诊断,传统的智能诊断方法上存在的主要问题是使用的模型架构较浅,模型泛化能力不足,从而限制了故障诊断能力[4]。而深度神经网络(deep neural networks,DNN)由于能够解决传统人工智能方法无法解决的问题而受到广泛的关注[5]。深度神经网络学习方式通常从原始数据出发,通过不断地迭代,自适应地将输入转换为更高、更抽象的表示层,从而达到更加精准的分类效果[6]。
近年来,国内外学者也开始将深度神经网络学习应用在故障诊断领域中,文献[7]提出了基于分层卷积网络的滚动轴承诊断方法,通过设计学习架构提取故障数据的特征,优化了卷积计算过程。文献[8]针对不同转速和随机噪声提出了一种无先验知识的机械数据深度自适应学习网络,又称Lifting Net,该模型能够对原始信号数据实现分层特征学习,并成功地对机械故障数据进行了分类。文献[9]提出了一种基于深度置信网络(deep belief network,DBN)诊断方法,从振动信号的频率分布中提取振动信号特征,通过表征学习电机工作状态,并将特征提取过程与分类任务相结合,实现了电机的故障诊断。文献[10]提出了一种卷积神经网络故障诊断方法,该方法采用原始振动信号通过数据增强产生更多的输入,在公共数据集上的振动信号上有着良好的效果,也适应于不同负载和噪声环境条件下。
基于深度神经网络建立故障诊断模型的诊断效果较好,但缺点是需要人工消耗大量时间去调整训练模型的参数,且模型的泛化能力有待提升。针对深度神经网络调参过于复杂的问题,文献[11]提出了深度森林模型(简称Deep Forest),该模型建立在随机森林[12]的基础上,并采用了类似于深度学习的深层结构,是一种有效的、参数可控制和能够适应不同规模数据的模型[13]。深度森林目前在癌症疾病诊断[14]、推荐系统[15]等方面取得了与深度神经网络相当的效果。
综上,为了解决现有深度学习调参复杂、参数赋值对结果影响大的问题,本文将深度森林引入故障诊断领域,建立基于深度森林的诊断模型,通过超参数分析获得了模型的最佳参数。首先,在简单工况下,通过对比分析关键参数,构建基于深度森林的故障诊断模型;然后将模型应用到复杂工况下来验证其泛化能力;最后与传统的分类模型及文献[8]的Lifting Net模型对比,以验证方法的有效性。
1 深度森林诊断模型
1.1 特征提取及预处理
针对噪声数据以及原始信号数据无法直接进行点对点比较等问题,本文提出一种输入数据集的预处理方法。首先,根据采样频率f,对获取的原始数据进行重采样分组,以确保每个旋转周期都使用相同的数据点进行采样。本文提取了原始数据集的9个时域特征:方根幅值,绝对均值,均方幅值,峭度,歪度,波形指标,峰值指标,裕度指标,脉冲指标和6个频域特征:均值,标准差,均方根频率,中心频率,频率集中率,频率峭度。
对每一个特征进行标准化处理,以确保特征向量在相同的范围内。标准化方程式为
(1)
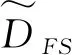
步骤1 获取原始数据集Doriginal;
步骤2 对Doriginal根据采样频率f进行重采样分组,得到数据集Dresample;
步骤3 对Dresample进行特征提取,获得时域特征集D′FS1及频域特征集D′FS2;
步骤4 将D′FS1及D′FS2根据公式(1)进行标准化处理得到D″FS1及D″FS2;
步骤5 依据原始数据信息,对两组特征集D″FS1及D″FS2进行标注Y;
通过以上5个步骤,即可得到时域的特征集DFS1={D″FS1,Y}和时域和频域相结合的特征集DFS2={D″FS1,D″FS2,Y}。
1.2 深度森林诊断模型构建
通过1.1节获取了特征数据集,为构建深度森林诊断模型提供了数据准备。深度森林是深度学习的一种,但与深度神经网络的结构差别较大。本文构建的深度森林诊断模型示意图如图1所示。模型每一层的构建都使用了两种随机森林(完全随机森林和普通随机森林),而每种随机森林也是决策树的集成,强化了集成学习的多样性和整体模型的泛化能力。
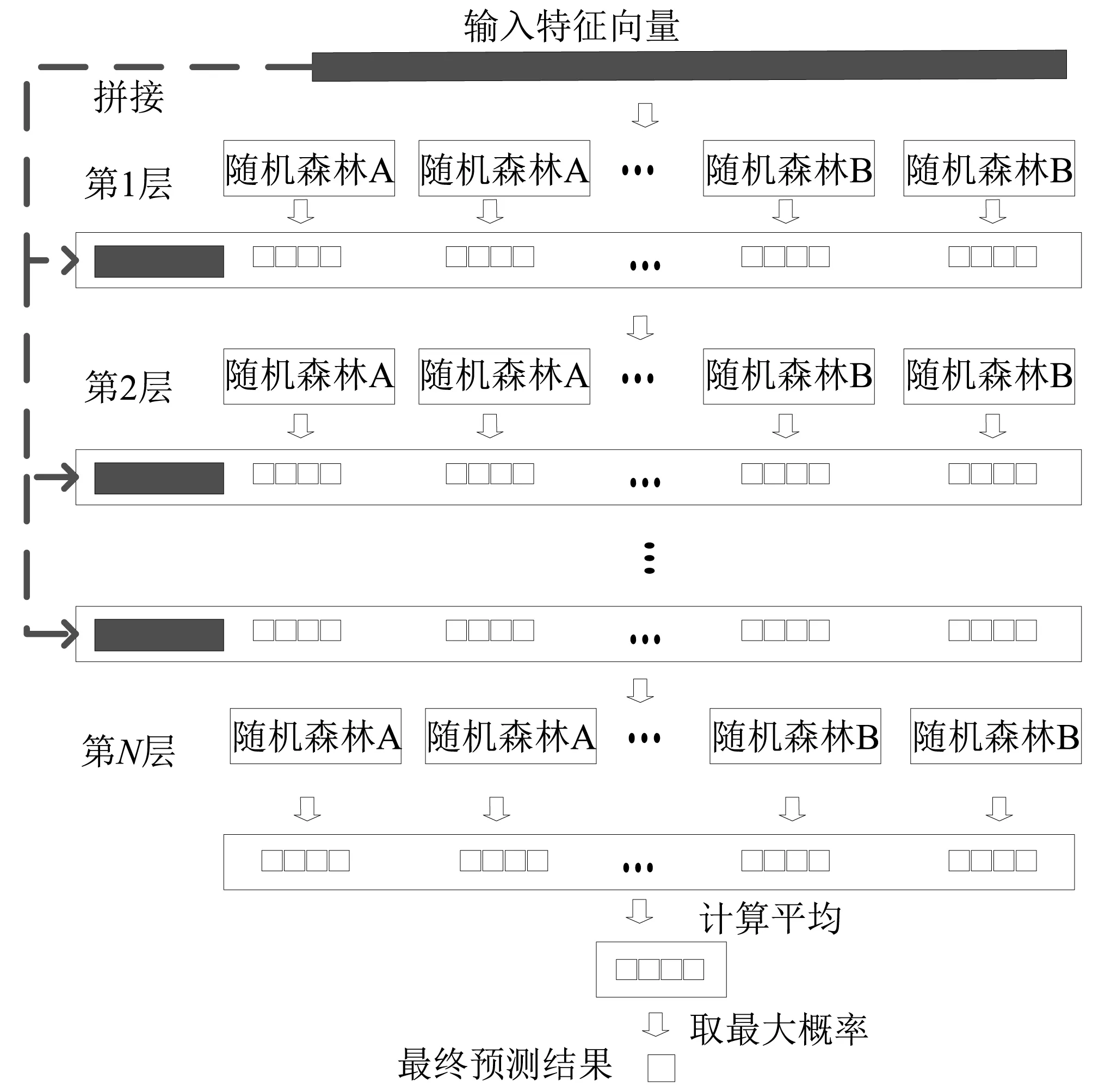
图1 深度森林诊断模型示意图

具体方法如下:对于第i个特征xi,它的信息增益是采用特征集DFS的熵与xi给的条件下DFS的经验条件熵H(DFS|xi)差异。信息增益函数Gain(·|·)的表达式为
Gain(DFS|xi)=H(DFS)-H(DFS|xi)
(2)
其中,
(3)
(4)
DFSxi=a={(x,y)∈DFS|xi=a}
(5)
DFSy=c={(x,y)∈DFS|y=c}
(6)
式中:Pi(DFS)为特征数据集DFS中特征xi所占总特征的比例,c是元素xi可能的类标签。
其中,每一个随机森林输出是一个类概率向量,如图2所示。
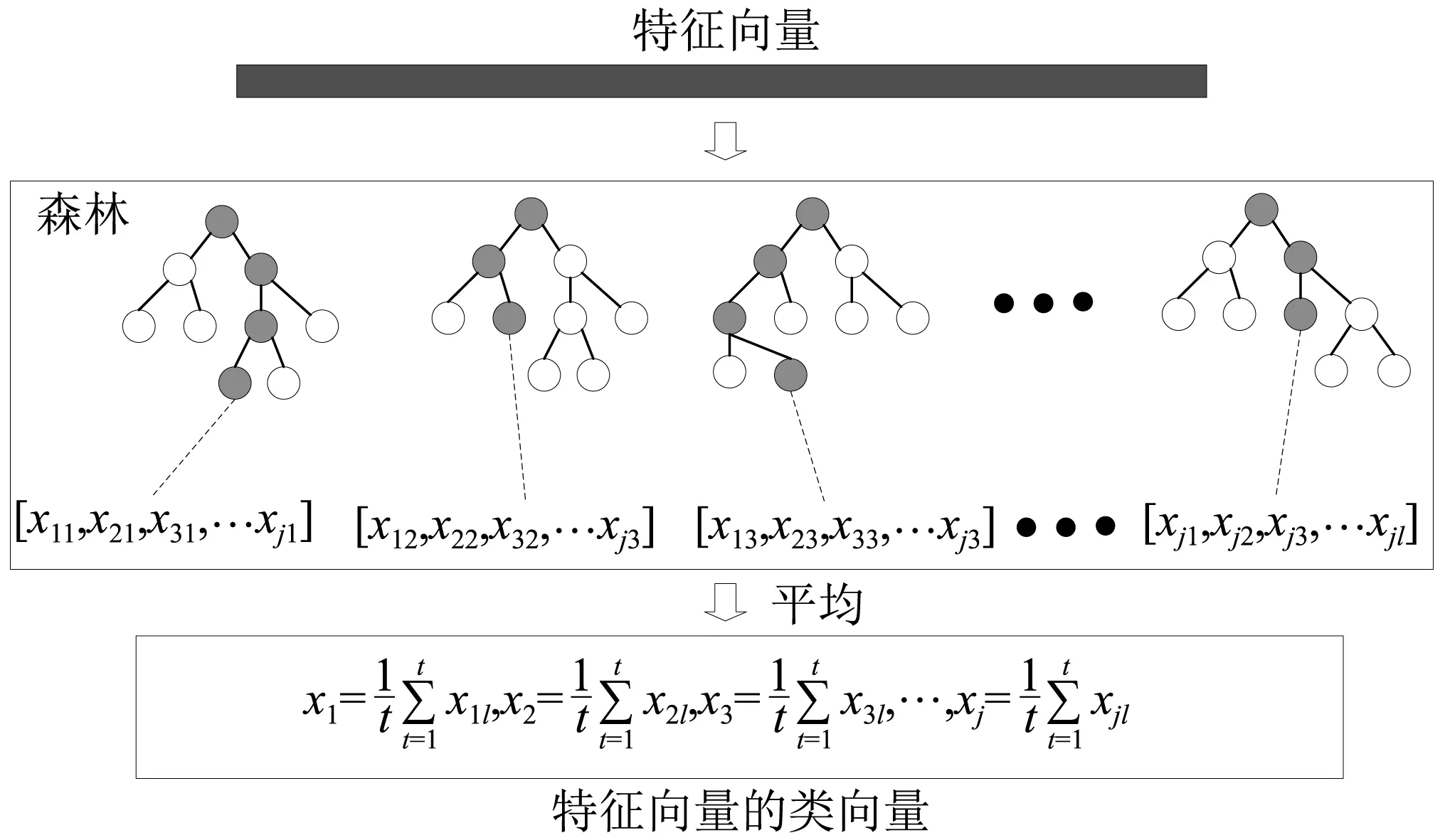
图2 类概率向量生成示意图
假设诊断数据有M个类,通过计算随机森林中相关实例在每棵决策树的叶子节点的比例,然后将每一个决策树输出的类别概率相加,按公式(7)取其平均,形成一个类概率向量X={x1,x2,…,xM}。
(7)
将每个随机森林进行K折交叉验证(K-fold Cross Validation),可以减少整体模型过拟合的风险。同时,当验证每一层结果时发现分类精度不再上升时就可以停止训练,以保证模型层数的自适应性,避免出现无限加层现象发生。本文的诊断模型训练步骤如下:
步骤1 初始化特征数据集DFS,T1个完全随机森林中有t1个决策树,T2个普通随机森林中有t2个决策树以及K值;
步骤2 将特征征数据集DFS通过式(2)~式(6)计算信息将特征排序并训练T1和T2个随机森林,并作K折交叉验证,并计算精度;
步骤3 两种随机森林中t1和t2个决策树根据式(7)的平均策略形成类的概率向量;
步骤4 将类概率向量与原始特征向量进行拼接输入下一层;
步骤5 将上述步骤2~3进行迭代,当分类的精度不再上升时,停止训练。
通过以上的几个步骤,最终得到诊断模型。
1.3 模型评判标准
深度森林模型选取的评判标准是精度(acc),精度是分类任务中最常用的性能度量,在数据挖掘及机器学习等领域有着广泛的应用,它表示着分类正确的样本占样本总数的比例。
设特征集DFS={(x1,y1),(x2,y2),…,(xm,ym)},包m含个特征。其中ym是xm的真实标签,要评估模型F的性能,就要把模型的预测结果F(xm)与真实标记ym进行比较,如式(8)所示
(8)
式中: Ⅱ(·)为指示函数; ·为真假时分别取1和0。
2 实验结果与分析
本节分为两组实验,首先分析一种简单工况下的实例以证明方法的有效性,再通过复杂工况下的实例来验证方法的泛化能力。
2.1 简单工况下的实验条件
简单工况采用的轴承数据来源于西储大学(Case Western Reserve University, CWRU),实验平台如图3所示,包括一个2马力的电机,一个转矩传感器和一个功率计。电机驱动端和风扇端轴承型号分别为深沟球轴承:6205-2RS JEM和6203-2RS JEM。实验平台使用电火花加工技术在轴承上布置了单点故障,分别为轴承外圈故障(outer race fault,OF)、轴承内圈故障(inner race fault,IF)和滚子故障(rolling fualt,RF),故障直径分别为0.018 cm、0.035 cm、0.053 cm和0.071 cm并将其重新安装到测试台上,为作比较实验还收集了一种正常轴承(normal bearing,NO)的信号数据。电机以恒定的速度运行,大约1 720 r/min,不同的负载(0~3 hp)由功率计提供,速度和马力数据的收集使用转矩传感器手动记录,振动数据使用加速度计进行收集,采样频率为12 kHz,本文实验选取了驱动端的轴承信号数据。

图3 西储大学故障数据实验平台
2.2 关键参数的确定
由1.2节得知,深度森林有四个关键参数,两种随机森林的个数T1与T2与每种随机森林决策树的个数t1与t2,本文通过一个1.1节预处理步骤构建得到了4 800个样本,每条样本包含9个时域特征,标记为特征集DFS1。
由于集成学习的多样性对整个模型的构建有着重要意义,对本文诊断算法来说,每一种随机森林数目不一致会让整个模型诊断效果具有不平衡性。因此,为了更好的体现诊断模型效果,本文将算法的参数设为T1=T2=T,t1=t2=t,同时,K折交叉验证设为3。
参数1: 随机森林决策树的个数t
该参数将固定每一次实验两种随机森林的个数T,将T设为2,而每个决策树的个数将从100棵树开始,每100棵树逐级增加棵数,并记录每次的诊断效果。模型的测试精度如图4所示,模型训练时间如图5所示。分析图4发现,在10组实验中,t的棵数与实验的测试集的精度(acc)没有呈现明显的正负关系,决策树棵数的改变对模型的诊断结果影响不大,这是集成学习的优点,诊断精度与多样性有关,而基分类模型(每一棵决策树就是一个基分类模型)的数目对整个模型效果的影响甚微。分析图5发现,由于决策树个数增加会增加整个模型内存的消耗,并且训练时间随决策树棵数增加而增加。在权衡决策树的棵数和精度与时间之间,本文将实验中每个随机森林中决策树的个数设为300棵。

图4 决策树棵数对模型精度(acc)的影响

图5 决策树的数目对模型训练时间的影响
参数2: 每种随机森林的个数T
在确定了参数1为300棵的基础上,通过参数1的测试,参数2的确定将每个随机森林中的决策树个数t设为300棵进行测试每种随机森林的个数T,T从2个开始,逐级增加1个进行测试。模型的测试精度如图6所示,模型训练时间如图7所示。
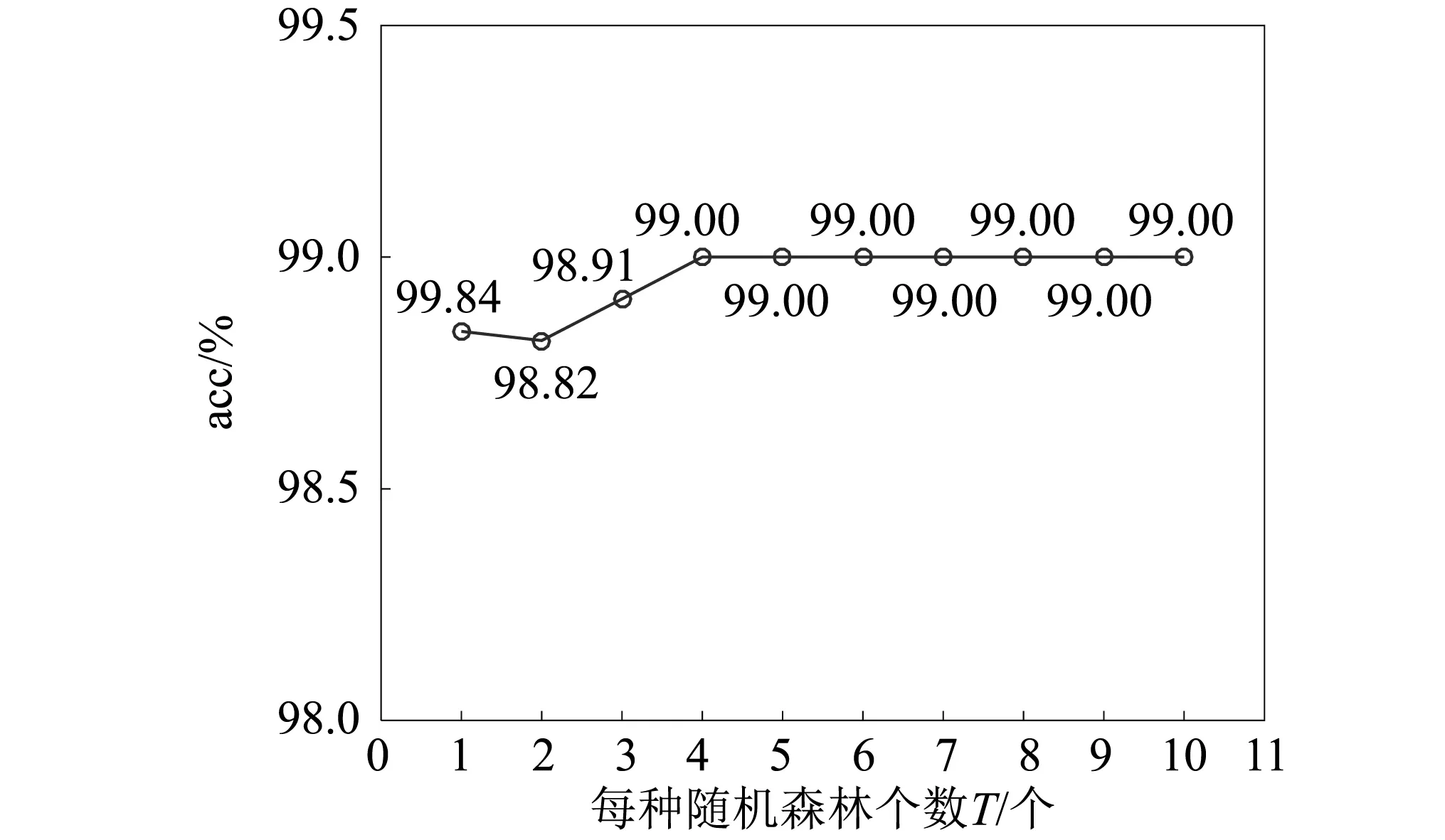
图6 随机森林个数对模型精度(acc)的影响

图7 随机森林的个数对模型训练时间的影响
分析图6发现,在10组实验中,在每组实验中,当随机森林个数达到4个以后,精度波动不高,稳定在99.00%。分析图7发现,随机森林的个数增加也会带来时间消耗的增加。
综合模型的精度及消耗的时间,每种随机森林的个数可选择4个及以上。在保证精度的前提下,为了节省整个模型的时间消耗,本文将T设置为4个。
2.3 简单工况下不同分类模型的对比
实验首先从4种状态的原始信号中进行特征提取预处理,构建两个特征数据集和,每个特征数据集包括4 800个样本,按照3∶1的比例建立训练数据集和测试数据集。图8节选是在0负荷下,采集故障严重程度为0.018 cm的不同故障信号样本和正常信号样本。

图8 简单工况下的时域图
将DFS1和DFS2分别输入支持向量机(support vector machine,SVM)以及随机森林(random forest)传统分类模型和本文分类模型(deep forest)经过3折交叉检验并比较平均精度,同时也与文献[8]的自适应的深度神经网络(lifting net)进行比较(原始信号输入),得到的结果如表1所示。分析表1,对比实验1、2、3、4和实验5、6发现,DFS2的结果都优于DFS1的结果,显然特征数量(维度)的增加可以提高分类精度。对比实验2、4、6发现,本文模型的平均诊断精度高于传统的SVM与RandomForest分类模型,但时间消耗更大。
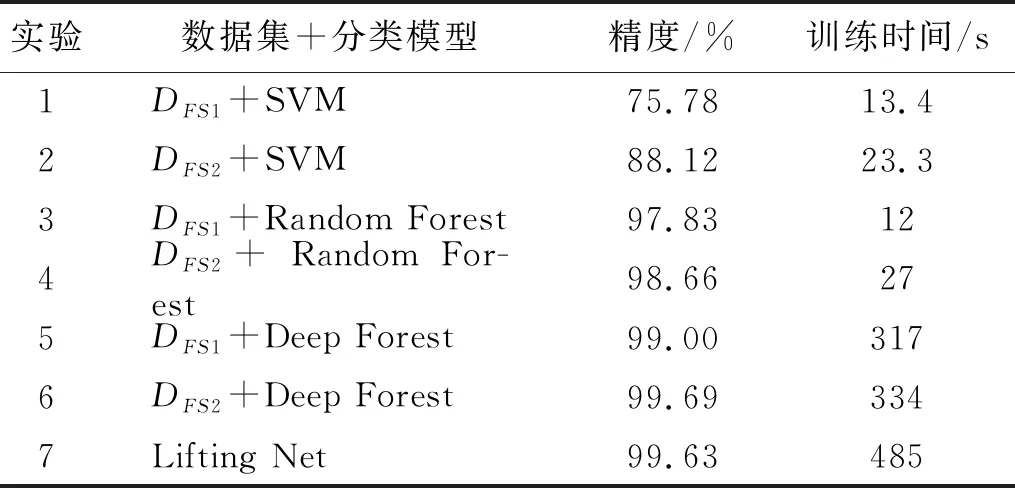
表1 简单工况下不同分类模型的精度与时间消耗比较
从实验6、7看,与Lifting Net对比,本文分类模型的精度接近,但时间消耗偏低,同时避免了复杂的调参过程。
2.4 复杂工况实验及分析
为了验证本文方法在复杂工况下的有效性,分别采集了不同转速下和不同方向上的滚动轴承信号。实验平台如图9所示,包括可调频电机、联轴器、传感器、轴承座等。实验采用SKF轴承,型号为30305。传感器采用的是PCB M603C01 ICP加速度传感器,一个安装在轴承座正上方(标记为Y方向),另一个安装在轴承座左侧方(标记为X方向)。采样频率为12 kHz,电机转速分别为800 r/min和1 396 r/min,信号采集系统采用的是DH5922N动态信号测试分析系统。

图9 实验平台
故障轴承的照片如图10所示,为了模拟轴承故障,采用线切割电火花加工技术,对深0.5 mm、宽0.5 mm轴承内圈、外圈和滚子制作了三种单点故障。

图10 故障轴承照片
实验获得的部分时域波形如图11所示,不同转速和不同的方向上的时域波形存在差异性,本节的数据相对于2.2节的公共数据集更接近于复杂工况。

图11 不同转速和不同方向的时域图
800 r/min和1 396 r/min下各有X、Y两个方向,每种状态采集时间截取为2 min,将四条记录(800_X,800_Y,1396_X,1396_Y)汇总成一条8 min的记录数据。四种轴承状态(正常、外圈故障、内圈故障、滚动体故障),并分别标记为NO,OF,IF,RF。采用1.1节中数据处理方法获得特征数据集DFS1与DFS2,每个特征数据集包含25 600个样本。输入本文分类模型,得到测试集DFS1的平均准确率达到92.54%,整个模型消耗时间为765 s。测试集DFS2的平均准确率达到93.15%,整个模型消耗时间为416 s。对比结果表明利用多维度的特征可以提高模型的诊断精度且能加快整个模型的收敛速度。
与简单工况类似,也将复杂工况下的2种数据集分别输入不同分类模型,得到复杂工况下不同模型的精度与时间消耗结果,如表2所示。

表2 复杂工况下不同模型的精度与时间消耗比较
对比表1、表2实验结果发现,即使受到不同转速和不同方向采集数据的影响,本文方法仍能得到较好的故障诊断结果,并且在不修改模型参数的情况下,该方法也能较好地适应新的诊断任务,有较强的泛化能力。
2.5 算法稳定性分析
为验证本文算法的稳定性,使用UCI机器学习库中Iris、Car以及Adult公共数据集,按照3∶1的比例划分测试集与训练集,分别输入到本文算法(参数设置为t=300,T=4)中进行验证,并与随机森林算法进行比较,对比结果,如表3所示。
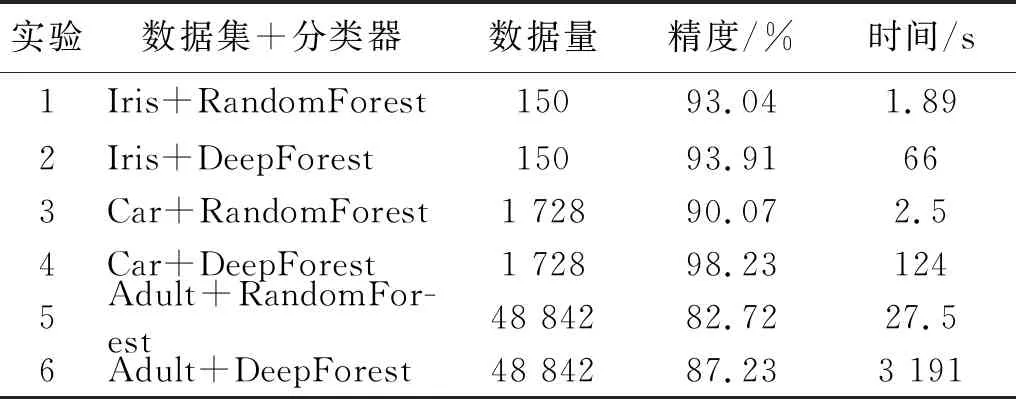
表3 UCI数据集在相同参数下的实验对比
分析表3发现,采用本文分析得到的参数设置得到的实验结果分别为93.91%、98.23%、87.23%,都优于随机森林的实验结果,表明本文方法具有较高的稳定性。
3 结 论
(1) 建立了一种基于深度森林的故障诊断模型,对模型的两个参数进行了多组对比试验,结果表明在给定数据规模的前提下,决策树棵数对整个诊断结果影响甚微;森林个数的增加对诊断结果有所提升,但达到一定数目后影响效果趋于平稳。
(2) 验证了该诊断模型在简单工况下诊断效果,并且在不修改模型参数的前提下,应用到复杂工况,验证了模型的泛化能力。
(3) 该模型相比于SVM,RandomForest诊断模型取得了较好的诊断结果,且接近于深度神经网络模型的诊断效果,但避免了繁杂的调参过程。
