粮食群仓的环境振动测试和角仓边仓振动响应分析

张大英，张帅枫，孙庆珍，梁醒培

粮食群仓的环境振动测试和角仓边仓振动响应分析

张大英1，张帅枫1，孙庆珍1，梁醒培2

（1.郑州航空工业管理学院土木建筑学院，郑州 450046； 2. 河南工业大学土木建筑学院，郑州 450001）

为了获取群仓准确的动力特性参数从而更合理地进行群仓的抗震设计，从粮食储藏工程考虑，对实际工程中一组三排五列的粮食群仓的振动特性进行了分析。基于结构振动理论和有限元数值分析，考虑结构对称性、荷载对称性和工程实际情况，制定了环境振动测试粮食群仓的优化方案；利用最小二乘法、五点三次平滑法和数字滤波的方法对测试信号进行了处理，得到了有效的测点加速度响应数据。基于控制理论和振动系统的运动方程，引入变换矩阵，推导了环境振动下利用测点加速度响应数据进行粮食群仓振型计算的公式，从而得到前四阶振型及对应的频率，各阶振型形态和模拟结果相同；前四阶频率计算值分别为2.28、3.45、6.37、8.26 Hz，对应模拟值分别为2.35、3.56、6.31、8.16 Hz，模拟值与计算值误差分别为3.07%、3.19%、0.94%、1.21%。进一步对角仓和边仓的振动反应进行分析，结果发现：两个仓体的第一阶振型均沿着粮食群仓整体的短轴方向，以剪切型为主，振型幅值基本一致，相邻仓体间的约束作用对一阶振动反应几乎没有影响；两个仓体的第二阶振型均沿着粮食群仓整体的长轴方向，仍以剪切型为主，但振型幅值不同，边仓小于角仓；两个仓体的第三阶振型形态为绕粮食群仓整体中心的扭转，短轴方向测点转动幅值大于长轴方向测点；随着相邻仓体间约束作用增强，两个仓体的第四阶振型形态和振型幅值均不同，角仓和边仓呈现不同的振动特性，角仓上靠近边仓测点振型以弯曲型为主，振型幅值相对较小，其他测点以剪切型或弯剪型为主，振型幅值相对较大；边仓受相邻3个仓体的约束作用，测点振型幅值都较小，而且靠近相邻仓体测点振型以弯剪型为主，中间列测点以剪切型为主。研究结果表明：相邻仓体间的相互约束作用对二阶及以上振型影响较大，根据振型形态和振型幅值分组进行粮食群仓中仓体的抗震设计更加切合实际，节约材料，降低成本。

粮食；粮仓；振动；有限元模拟；环境振动测试

0 引 言

2020年以来，随着新冠肺炎疫情在海内外的蔓延，多国政府宣布限制粮食出口，因此具有丰厚的粮食储藏在各国至关重要。从目前情况看，政策性库存创历史新高，主产区普遍高装满储，夏粮收购面临一定仓容压力，要通过加快库存消化、增加储粮设施等措施，确保收购顺利进行[1]。由此看来，在全国范围内大力建设粮仓是大势所趋，是保障国内民生的重要工程。粮食群仓由于其仓容量大、机械化程度高、占地面积小等特点，是全国性重要粮食物流节点中大规模仓储建设的主导仓型。因此，采用合理的计算方法进行粮食群仓设计至关重要，而且从长远来看，作为国家战略发展储备的粮仓应能够抵御如地震等各种自然灾害。鉴于此，自20世纪80年代以来，粮仓抗震问题便成为最活跃的课题之一，也取得了诸多研究成果。20世纪90年代，各专家学者[2-4]主要通过单仓模型的地震模拟振动台试验研究单仓的动力特性和地震反应问题。进入21世纪以后，刘增荣等[5]开始将模态试验测试方法应用于单仓结构中获得结构的动力特性参数；一些专家学者[6-7]开始对小规模群仓展开研究，并提出了自振频率的回归计算公式和修正的基底剪力计算公式；还有一些学者[8-11]主要研究散料-仓壁的动力相互作用，发现地震时处于弹性地基上的筒仓减震效果明显。随后，相关学者[12-13]进行基础-筒仓-散料的动力相互作用研究，发现深仓需要考虑两者的相互作用，同样验证了弹性地基上筒仓结构内部受力更合理的研究成果，并给出了考虑三者动力相互作用的钢筋混凝土筒仓抗震设计方面的一些建议。此外，一些专家学者主要考虑场地类别和不同地震波输入下，地基-筒仓[14-19]或地基-基础-筒仓[20]动力相互作用对结构体系的影响，研究发现场地土特性、基础埋深对土-结构相互作用影响显著，结构地震力发生折减，场地越软，折减越明显，结构的位移反应增大，且场地越软增大越显著。随着国际局势的变化，考虑到国家战略发展的需要，近年来地下粮仓[21-26]的研究和应用也在逐步进行中，如装配式技术和组合结构技术的新型地下粮仓结构设计方案的提出，装配式地下粮仓钢-混组合仓壁节点力学性能的有限元分析，为地下粮仓的进一步研究和设计应用提供了参考。

从目前的研究成果来看，国内外对粮仓的抗震研究体现在多个方面，而且从早期就开展了粮仓动力特性参数的研究，包括地震模拟振动台试验和环境激励模态试验，但主要是单仓，并且目前规范[27]中主要以单仓的研究结果为依据进行群仓的结构设计，过于保守，与实际情况不相符合，尤其是对于大规模群仓如果简单依据单仓设计经验则更加不符合实际。因此，为了实现粮食群仓的抗震优化设计，对粮食群仓进行环境振动测试并分析其振动反应从而获得不同位置仓体的有效动力特性参数，这些参数是进行结构合理抗震设计的核心和根本。基于环境振动测试数据进行了粮食群仓中角仓和边仓动力特性参数的理论计算，并与数值模拟分析的角仓和边仓的振动反应进行细化对比分析，明确角仓和边仓各自的振动反应特点，指出进行群仓抗震结构设计时应考虑仓体所处位置不同所分配地震力的不同，以期优化结构设计，降低工程成本。

1 粮食群仓环境振动测试

1.1 试验粮食群仓

图1所示为进行环境振动测试的粮食群仓，共有15个同样的仓体按照三排五列的方式整体浇筑在一起。该粮食群仓右侧设置了一座工作塔，通过连廊与群仓上部建筑物相连，经过工作塔内的电梯到达群仓顶部的仓上建筑。从室外地面到粮食群仓顶盖表面的高度为30.5m，筒壁支撑与仓身之间的环梁到粮食群仓顶盖的高度为25 m，仓上建筑物高度为4m，顶盖的厚度为100mm，仓壁厚度为180mm，群仓内半径为3.82m，外半径为4 m。试验过程中，每个仓体内装满小麦，仓体之间的星仓内没有装粮。

1.2 试验仪器设备

测试用到的仪器设备为江苏东华测试技术有限公司的DH5922型动态信号采集仪系统和DH610型传感器，该系统的采样频率范围为10 Hz～128 kHz，使用了DH610型传感器的加速度档进行粮食群仓的加速度数据信号采集。

1.3 环境振动测试方案

图1所示粮食群仓结构，单个仓体之间在相切处浇筑成整体，根据结构动力学的相关知识并结合有限元分析结果，粮食群仓的自振特性表现为低阶（前三阶）整体振动反应、高阶（4阶及以上）局部振动反应，即高阶时组成群仓的单个仓体的局部振动反应具有各自的特点。根据这些特点并考虑群仓的对称特性和现场操作实际情况，对处于群仓4个角的仓体（图2中角仓1、角仓5、角仓11、角仓15）、第一列中间位置的仓体（图2中边仓6）、第三排左起第2列（图2中边仓12）、第3列（图2中边仓13）仓体布置测点进行环境振动测试。角仓1和角仓11作为主要研究对象，测点布置数量多；角仓5和角仓15主要作为角仓1和角仓11的校核，测点布置数量少。边仓12和边仓13作为与角仓进行高阶振动反应对比的主要对象，布置3列测点；边仓6布置1列测点。

注：C11、C12为参考点，C56～C100为其他测点。图中单位为mm。

Note: C11 and C12 are reference points, and C56-C100 are the other measuring points. The unit in the plan is mm.

图2 粮食群仓平面图

Fig.2 Plan of grain group silos

此次振动反应细化分析中以角仓11和边仓12为主要对象进行分析对比，两个仓的测点平面详细位置见图2，将测点距地面的高度、采样批次和所要测试的加速度方向列于表1，表1的批次代表环境振动测试时的采样批次。由于测点数量多，需要分批次进行测试，参考点为1号角仓上的测点C11和C12，其距地面高度分别为30.5和24.5 m，C11和C12均需要测试法向和切向加速度。

表1 测点C56～C100采样批次及加速度方向

注：R+代表单个仓体自身平面圆的外法线方向；T+代表测点切向方向，逆时针为正。

Note: R+ represents the outer normal direction of the plane circle of the single silo; T+ represents the tangential direction of the measuring point and the anticlockwise direction is positive.

1.4 测点加速度信号及预处理

对粮食群仓进行环境振动测试，首先通过有限元模拟的方法算得所需要的结构最大频率max，然后根据采样定理的条件f≥2max设定合适的采样频率f，此外，采用滤波器进行抗混滤波，设定上限频率，消除不在考虑范围内的其他频率信号的影响。据此，测试时采样频率以100和50 Hz为主，上限频率设置为30 Hz进行加速度数据采集。对每一批测点进行多次数据采集完成后从中选择无异常突变的采样数据进行分析。由于采集得到的振动信号中通常会叠加有噪声信号，包括50 Hz的工频及其倍频程等周期性的干扰信号，以及不规则的随机干扰信号。随机干扰信号往往频带较宽，有时高频成分占比例很大，这样利用采集的离散数据描绘成的振动曲线上会呈现出许多毛刺，很不光滑。为了消除上述干扰信号的影响，提高振动曲线光滑度，因此还需对采样数据进行平滑处理。此外，数据平滑还可以消除信号的不规则趋势项，这些不规则趋势项通常是由于测试仪器受到某些意外干扰，造成个别测点的采样信号产生偏离基线较大而产生的，对数据进行多次平滑处理后，得到一条光滑的趋势项曲线，用原始信号减去趋势项，可以消除信号的不规则趋势项。五点三次平滑法[28]是进行时域和频域信号平滑处理的一种有效方法，其利用最小二乘法原理对离散数据进行三次最小二乘多项式平滑，能够减少时域数据中混入振动信号的高频随机噪声。但是需要注意平滑次数的确定，可以通过多次试算后最终确定平滑次数的数值，防止平滑次数太多导致识别参数误差增大。通过多次试算，本文确定平滑次数为3。

通过自功率谱分析，预估每次采样的频率变化范围，利用低通数字滤波的方式滤除不感兴趣或干扰频率。通过消除多项式和不规则趋势项，以及平滑曲线的方法将高频干扰信号剔除。经过上述信号预处理就可以得到有效的加速度响应数据。

图3a截取了第三批测试中第一次采样的参考点C11在时间段0～81.91 s之间的加速度数据作为示例进行分析。利用最小二乘法消除多项式趋势项，再利用五点三次平滑法和数字滤波方式对曲线进行处理得到图3b所示的测点C11加速度曲线。比较图3a、b可以看出，经过数据处理后，加速度曲线幅值较原始曲线幅值降低，而且曲线更加平滑。

2 环境振动下粮食群仓振动计算理论

根据自由度为的振动系统的运动方程式：

式中、和为结构质量、阻尼和刚度矩阵；()为连续时间上的位移向量；()为激励力向量。

根据控制理论，将运动方程式（1）进行转换，得到离散时间上的状态空间模型表达式：

式中+1和为时刻的状态输入和输出向量；为离散时间上的状态矩阵；2为输出矩阵；和为过程噪声和测量噪声。

利用所测得的加速度数据信号构建Hankel矩阵（以下称矩阵）[29]，并进行QR分解[30]。

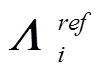
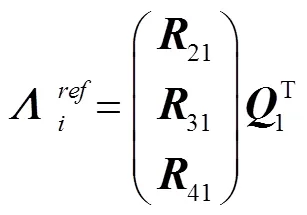
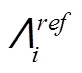
同样方式得到：

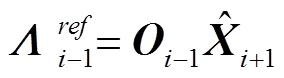
将系统矩阵进行特征值分解，求解得到特征值和特征向量，进一步地求解连续时间上的系统矩阵（=exp(Δ)，Δ为时间间隔）的特征值和特征向量，公式如下：

计算得到原系统的复模态振型矩阵：

=2（11）

式中代表系统的阶数。

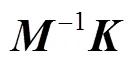
实际测试时所得到的结构模态数目通常小于结构自由度和结构上的测点数目，所以需要对公式（13）进行变换：

式中为所能测得的模态的数目；Re{}为振型实部。

再利用变换矩阵，得到原系统的实模态振型如下

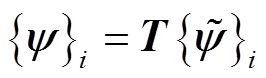
3 角仓边仓振动响应分析

3.1 理论计算

根据振型计算理论，定义式（19）所示的判定准则，以频率为横轴，系统阶数为纵轴，系统阶数依次取2、4、6、8…max（一个较大值，通过多次试算确定），判断频率、阻尼或振型是否满足该判定准则，如果满足则将对应频率、阻尼和振型的符号描绘于图中，当三者都满足时，设置稳定极点符号，并描绘于图中，由此描绘的图形为稳定图。对应某一频率处的稳定极点符号描绘成一条“竖直线”，称为稳定极值线，根据稳定极值线可以确定系统的各阶频率值。

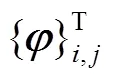
满足式（19）的判定准则，绘制R向和T向各批次测点的稳定图如图4所示，同时将各测点的自功率谱叠加曲线绘制于图中，利用曲线峰值和稳定极值线共同判定系统的频率值。

注：“·f”代表频率稳定，“·fv”代表频率和振型稳定，“·f z”代表频率和阻尼比稳定，“*”代表稳定极点。

Note: ‘·f ’ represents stable frequency, ‘·fv ’ represents stable frequency and mode shape, ‘·fz ’ represents stable frequency and damping ratio, and ‘ * ’ represents stable poles.

图4 测点稳定图

Fig.4 Stabilization diagram of the measuring points

根据稳定图4，确定系统的前四阶频率值，分别为2.28、3.45、6.37和8.26 Hz。根据上述振型计算理论，将对应频率代入可以得到对应的前四阶振型。将粮食群仓中所有测试每个仓体的R向和T向的各批次加速度数据分批独立进行分析，基于参考点进行归一化处理后作出相应的振型图。由于粮食群仓为实际工程结构，根据实际情况布设的测点数目有限，因此不能类似数值模拟方式针对每个仓体绘制连续完整的振型图，但是可以根据测试数据利用上述的理论方法求解各个测点的振型值，并绘制出单列测点和同一高度处一环测点的振型曲线，并与数值模拟相应位置处的振型曲线进行对比分析。

3.2 数值模拟

3.2.1 参数和构件单元类型定义

不考虑各个仓体内的小麦对粮食群仓整体的刚度贡献作用，将小麦质量均匀地离散分布到仓壁内表面的各个节点上。材料参数列于表2中。粮食群仓中仓顶盖、仓壁、漏斗、内柱均采用SOLID45单元，小麦采用MASS21单元。

表2 材料参数

3.2.2 数值结果

有限元分析得到的粮食群仓的前四阶频率值分别为2.35、3.56、6.31和8.16 Hz，与前述3.1节识别得到的频率值比较接近，各阶频率值误差分别为3.07%、3.19%、0.94%、1.21%。

粮食群仓的前四阶振型见图5，第1阶振型主要呈现为粮食群仓整体沿短轴方向的剪切变形，仓体上部振动反应大于下部；第2阶振型主要呈现为粮食群仓整体沿长轴方向的剪切变形，两列短轴方向的边仓上部振动反应明显大于其他仓体；第3阶振型主要呈现为粮食群仓整体沿中心点的扭转变形，而且4个角仓上部振动反应较其他仓体更加明显；第4阶振型主要呈现为各个仓体的局部振动反应，而且不同位置仓体的振动反应不同。

4 结果与分析

根据图5所示粮食群仓整体振型数值云图可以看出，当仓体内储粮对称时，振型具有轴对称特性。为了深入分析不同位置仓体振动反应的差异性，对图2中11号角仓和12号边仓进行细化分析。

将11号角仓上测点C71～C75和12号边仓上测点C91～C95的R向前三阶振型立面绘制于图6中。11号角仓和12号边仓不同高度处的测点第四阶振型平面图和立面图分别绘制于图7和图8中。

图6a第1阶振型，为沿着图2所示轴方向即粮食群仓整体的短轴方向的振动反应，11号角仓和12号边仓的振型模拟值基本一样，它们的振型试验值也基本一样，两者的模拟值均大于试验值。当产生向粮食群仓整体短轴方向的振动反应时，角仓和边仓所处位置不同，但受相邻仓体的约束程度相差不大，因此振型幅值差异不大。

图6b第2阶振型，为沿着图2所示轴方向即粮食群仓整体的长轴方向的振动反应，11号角仓试验值和模拟值曲线吻合良好，曲线的变化形态近似剪切型，从仓体下部到仓体上部振型幅值由小变大；12号边仓试验值和模拟值曲线吻合良好，曲线的变化形态亦近似剪切型，与角仓一致，但边仓振型幅值略小于角仓，靠近仓体顶部振型幅值较仓体下部减小更多。主要是由于两者在粮食群仓整体中的位置不同引起，边仓与其周边三个仓体有相互约束作用，角仓处于粮食群仓的角部，受相邻仓体的约束程度明显低于边仓。

观察图6c第3阶振型，11号角仓上测点C60～C56沿着切向（向）振型幅值明显大于该角仓上测点C75～C71和12号边仓上测点C95～C91沿着切向（向）的振型幅值，主要是由于测点C60～C56位于粮食群仓整体短轴方向，振动反应更明显，而测点C75～C71和测点C95～C91位于粮食群仓整体长轴方向，振动反应相对短轴方向弱。总体描述这三列测点的振动反应呈现扭转形态，与图5c所示的粮食群仓整体的扭转振型相一致。

图7给出了11号角仓和12号边仓上距地面高度分别为5.5、15.5、19.5、24.5和30.5 m处的测点第4阶振型平面图。分析图7a，11号角仓各高度处测点振型试验值与模拟值吻合较好，振动反应形态一致；高度为5.5 m处各测点R向振型幅值差异不大，高度为15.5、19.5和24.5 m处角仓外部两个测点向着R+方向振动，靠近边仓方向的四个测点向着R-方向振动，靠近12号边仓的测点振型幅值较其他位置小，高度为30.5 m处测点振动反应形态与仓体中部三环测点相似，但是振型幅值较小，主要是由于粮食群仓顶部有仓上建筑，对仓顶部影响较其他位置大。分析图7b，12号边仓各高度处测点振型试验值与模拟值吻合较好，振动反应形态一致；各高度处测点振型幅值差异较小，但边仓振型平面与角仓振型平面不同，大致呈现为中间测点和两侧测点振型相反的趋势，进一步说明了仓体所处位置不同，则振动反应会有所不同。

注：振型模拟值和试验值以角仓或边仓曲线为基准向内外振动；和代表仓体的对称轴。

Note: The simulated and experimental vibration mode based on the corner or side silo;andrepresent the axis of symmetry of the silo.

图7 角仓和边仓不同高度处振型平面图

Fig.7 Plan of vibration mode of the corner and side silos at different heights

图8为11号角仓和12号边仓每列测点第4阶振型立面图。角仓立面振型和边仓立面振型形态不同，各列测点振型试验值和模拟值吻合较好。

分析图8a，靠近角仓外部的四列测点的振型形态以弯剪型为主，仓体中部振型幅值大、上部次之、下部最小；靠近边仓的两列测点的振型幅值相对较小，而且离边仓最近的那一列测点的振型幅值最小，振型以弯曲型为主，另一列测点振型以剪切型为主；靠近角仓外部的两列测点振动反应沿着R+方向，另四列测点振动反应沿着R-方向。分析图8b，边仓各列测点振型幅值相对较小，中间列测点振型形态以剪切型为主，另两列测点振型形态以弯剪型为主；各列测点的振型幅值也大致呈现为中部幅值大、上部次之、下部最小的规律；靠近角仓的那一列测点的幅值相对更小。角仓和边仓的第四阶振型立面图更进一步说明了角仓和边仓在粮食群仓中的位置不同引起了不同的相互约束作用，从而对各仓体振动反应产生不同影响。

5 结 论

1）阐述了环境振动下利用测点加速度响应数据进行粮食群仓振型的理论计算方法，考虑到结构模态数目通常小于结构实际的自由度和结构上的测点数目，通过对振型实部进行SVD分解，得到变换矩阵后将复模态振型矩阵变换为实模态振型矩阵，得到了测点的有效振型。

2）针对粮食群仓典型位置的仓体进行了测点布置，利用试验获得的加速度响应数据计算得到仓体前四阶振型和频率，频率值分别为2.28、3.45、6.37和8.26 Hz；利用有限元方法对粮食群仓进行了数值模拟，得到了群仓整体以及各个仓体的前四阶振型和频率，频率值分别为2.35、3.56、6.31和8.16 Hz；两者所得各阶振型形状相同，频率值接近，各阶频率值误差分别为3.07%、3.19%、0.94%、1.21%。

3）对粮食群仓第一排的一个角仓和一个边仓测点振型的试验值和模拟值进行了振动响应分析，振型形状相同；角仓和边仓第一阶振型形态和幅值基本一致，没有明显的差异性，说明此阶振型中仓体之间的相互约束作用不明显；角仓和边仓第二、三阶振型形态一致，但振型幅值不同，说明仓体之间的相互约束作用因仓体所处位置不同而不同；角仓和边仓第四阶振型形态和振型幅值均不同，说明随着振型阶数的增加，仓体所受相邻仓体的约束作用更加明显，而且处于不同位置仓体受约束作用的程度明显不同。

根据上述结论，利用不利仓体的内力和振型进行粮食群仓整体抗震结构设计显得保守，并在一定程度上会浪费材料，群仓规模越大此种方法越不尽合理。将仓体在粮食群仓中因位置不同而受到相邻仓体约束作用不同的特性加以考虑，根据振型形态和幅值大小将仓体分成不同组进行抗震结构设计，则更加符合各仓体的实际力学特性，而且能够在保证受力合理的基础上节约材料，降低工程成本。

[1] 夏青. 大国粮仓[J]. 农经，2020(5)：34-39.

Xia Qing. Barn of great power[J]. Agriculture Economics, 2020(5): 34-39. (in Chinese with English abstract)

[2] 施卫星，朱伯龙. 钢筋混凝土圆形筒仓地震反应试验研究[J]. 特种结构，1994，11(4)：55-58.

Shi Weixing, Zhu Bolong. The experimental study of earthquake response of R. C. cylinder silos[J]. Special Structures, 1994, 11(4): 55-58. (in Chinese with English abstract)

[3] 马建勋，梅占馨. 筒仓在地震作用下的计算理论[J]. 土木工程学报，1997，30(1)：25-30.

Ma Jianxun, Mei Zhanxin. Study on calculating theory of seismic response of silos[J]. China Civil Engineering Journal, 1997, 30(1): 25-30. (in Chinese with English abstract)

[4] 徐荣光，胡声松. 圆筒仓的自由振动[J]. 噪声与振动，1999(2)：18-20.

Xu Rongguang, Hu Shengsong. The free vibration of the cylinder silos[J]. Noise and Vibration Control, 1999(2): 18-20. (in Chinese with English abstract)

[5] 刘增荣，黄义. 贮仓结构参数的频域识别[J]. 振动与冲击，2001，20(1)：79-81.

Liu Zengrong, Huang Yi. Frequency domain identification of storehouse structure parameters[J]. Journal of Vibration and Shock, 2001, 20(1): 79-81. (in Chinese with English abstract)

[6] 王命平，孙芳，高立堂，等. 筒承式群仓的地震作用分析及试验研究[J]. 工业建筑，2005，35(10)：29-32.

Wang Mingping, Sun Fang, Gao Litang, et al. Study of earthquake action and tests of multi-silo supported by cylinder[J]. Industrial Construction, 2005, 35(10): 29-32. (in Chinese with English abstract)

[7] 滕锴，王命平，耿树江. 筒承式群仓有限元分析及自振基频的简化计算[J]. 特种结构，2006，23(4)：34-36.

Teng Kai, Wang Mingping, Geng Shujiang. Finite element analysis and simplified calculation of natural vibration fundamental frequency of group silos[J]. Special Structures, 2006, 23(4): 34-36. (in Chinese with English abstract)

[8] Nateghi F, Yakhchalian M. Seismic behavior of silos with different height to diameter ratios considering granular material structural interaction[J]. IJE Transaction B:Applications, 2012, 25(1): 27-37.

[9] Zhang P, Zhao Y. Seismic behavior of steel silos considering granular material-structure interaction: Research advances and natural vibration property analysis[J]. Spatial Structures, 2014, 20(3): 88-96.

[10] Jagtapa P, Chakrabortya T, Matsagara V. Nonlinear dynamic behavior of granular materials in base excited silos[J]. Mechanics of Advanced Materials and Structures, 2015, 22(4): 313-323.

[11] Nateghi F, Yakhchalian M. Seismic behavior of reinforced concrete silos considering granular material-structure interaction[J]. Procedia Engineering, 2011, 14: 3050-3058.

[12] 黄义，尹冠生. 考虑地基-结构-散粒体相互作用时贮仓结构的静动力研究[I]：实验研究[J]. 应用力学学报，2002，19(3)：40-45.

Huang Yi, Yin Guansheng. Silo's static and dynamic testing study on considering the interaction of foundation, structure and bulk Solid—[I] Static and dynamic testing study[J]. Chinese Journal of Applied Mechanics, 2002, 19(3): 40-45. (in Chinese with English abstract)

[13] 黄义，尹冠生. 考虑地基-结构-散粒体相互作用时贮仓结构的静动力研究[II]：有限元分析[J]. 应用力学学报，2003，20(2)：124-128.

Huang Yi, Yin Guansheng. Silo's static and dynamic testing study on considering the interaction of foundation, structure and bulk Solid—[II] FEM study[J]. Chinese Journal of Applied Mechanics, 2003, 20(2): 124-128. (in Chinese with English abstract)

[14] 王瑞萍. 筒承式筒仓和地基相互作用的地震反应分析[D]. 青岛：青岛建筑工程学院，2003.

Wang Ruiping. Seismic Response Analysis of the Interaction Between Silo and Foundation[D]. Qingdao: Qingdao University of Technology, 2003. (in Chinese with English abstract)

[15] 曹彩芹，黄义，刘彤，等. 大型筒仓与地基动力相互作用研究[J]. 空间结构，2004，10(4)：57-59.

Cao Caiqin, Huang Yi, Liu Tong, et al. Dynamics analysis of interaction between large silo structure and its foundation[J]. Spatial Structures, 2004, 10(4): 57-59. (in Chinese with English abstract)

[16] Durmuş A, Livaoglu R. A simplified 3 D.O.F. model of a FEM model for seismic analysis of a silo containing elastic material accounting for soil-structure interaction[J]. Soil Dynamics and Earthquake Engineering, 2015, 77: 1-14.

[17] 王命平，孙芳，刘伟，等. 筒仓与地基相互作用对支承柱端弯矩的影响[J]. 世界地震工程，2008，24(2)：127-130.

Wang Mingping, Sun Fang, Liu Wei, et al. The effect of the silo-foundation interaction on the moment of supporting columns[J]. World Earthquake Engineering, 2008, 24(2): 127-130. (in Chinese with English abstract)

[18] 贾明明. 考虑土-结构相互作用预应力混凝土筒仓地震反应分析[D]. 西安：西安建筑科技大学，2015.

Jia Mingming. Seismic Response Analysis of the Prestressed Concrete Silo Considering Soil-structure Interaction[D]. Xi'an: Xi'an University of Architecture and Technology, 2015. (in Chinese with English abstract)

[19] Zhang K, Chen T N, He L. Damping behaviors of granular particles in a vertically vibrated closed container[J]. Powder Technology, 2017, 321: 173-179.

[20] 马瑞挺，孟云芳. 考虑仓壁-基础-地基相互作用时筒仓结构的有限元分析[J]. 宁夏工程技术，2012，11(2)：145-147.

Ma Ruiting, Meng Yunfang. Finite element analysis of silo considering the interaction of wall-basis-foundation[J]. Ningxia Engineering Technology, 2012, 11(2): 145-147. (in Chinese with English abstract)

[21] 王振清，揣君，刘永超，等. 地下粮仓的结构设计研究现状与新进展[J]. 河南工业大学学报：自然科学版，2019，40(5)：132-138.

Wang Zhenqing, Chuai Jun, Liu Yongchao, et al. Current situation and new progresses of structure design of underground silos[J]. Journal of Henan University of Technology: Natural Science Edition, 2019, 40(5): 132-138. (in Chinese with English abstract)

[22] 张庆章，田栓柱，贾玲玲，等. 新型散装粮食半地下平房仓的自振特性及地震响应分析[J]. 工程抗震与加固改造，2020，42(4)：31-39.

Zhang Qingzhang, Tian Shuanzhu, Jia Lingling, et al. Natural vibration characteristics and seismic response analysis of a new type of semi-underground horizontal warehouse to storage bulk grain[J]. Earthquake Resistant Engineering and Retrofitting, 2020, 42(4): 31-39. (in Chinese with English abstract)

[23] 王振清，揣君，王录民，等. 装配式地下粮仓钢-混组合仓壁节点力学性能有限元分析[J]. 农业工程学报，2019，35(24)：298-306.

Wang Zhenqing, Chuai Jun, Wang Lumin, et al. Finite element analysis on mechanical properties of joint in precast steel plate-concrete composite wall of underground granary[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(24): 298-306. (in Chinese with English abstract)

[24] 金立兵，梁新亚，霍承鼎，等. 地下混凝土筒仓仓壁力学性能工程试验与数值分析[J]. 土木与环境工程学报（中英文），2020，42(3)：40-45.

Jin Libing, Liang Xinya, Huo Chengding, et al. Engineering test and numerical analysis of underground concrete silo[J]. Journal of Civil and Environmental Engineering, 2020, 42(3): 40-45. (in Chinese with English abstract)

[25] 揣君，王录民，何毅，等. 地下圆形粮仓钢板－混凝土组合仓壁弹性应力计算公式推导与验证[J]. 河南工业大学学报：自然科学版，2021，42(1)：108-113，123.

Chuai Jun, Wang Lumin, He Yi, et al. Derivation and verification of the formula for calculating the elastic stress of steel plateconcrete composite wall of underground silo[J]. Journal of Henan University of Technology: Natural Science Edition, 2021, 42(1): 108-113, 123. (in Chinese with English abstract)

[26] 张昊，孟庆婷，陶元庆，等. 地下粮仓塑料-混凝土防水体系抗水压试验[J]. 农业工程学报，2020，36(21)：292-299.

Zhang Hao, Meng Qingting, Tao Yuanqing, et al. Experiment on water pressure resistance of plastic-concrete waterproof system of underground granary[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2020, 36(21): 292-299. (in Chinese with English abstract)

[27] 钢筋混凝土筒仓设计标准：GB50077-2017[S]. 北京：中国计划出版社，2017.

[28] 王济，胡晓. MATLAB在振动信号处理中的应用[M].北京：中国水利水电出版社，2006.

[29] 张大英，王录民，王树明. 一种获取结构实模态振型的方法[J]. 应用基础与工程科学学报，2014，22(2)：375-383.

Zhang Daying, Wang Lumin, Wang Shuming. An improved method for the determination of real vibration mode shapes[J]. Journal of Basic Science and Engineering, 2014, 22(2): 375-383.(in Chinese with English abstract)

[30] 杨明，刘先忠. 矩阵论（第二版）[M]. 武汉：华中科技大学出版社，2005.

[31] Overschee P V, Moor B D. Subspace Identification for Linear Systems: Theory-Implementation-Application[M]. Dordrecht, Netherlands: Springer, 1996.

Ambient vibration test of grain group silos and vibration response analysis of the corner and side silos

Zhang Daying1, Zhang Shuaifeng1, Sun Qingzhen1, Liang Xingpei2

(1.,,450046,; 2.,,450001,)

Accurate dynamic parameters are essential to more reasonably design grain group silos under earthquake action. In this study, the vibration characteristics of large-scale grain silos were analyzed, considering 15 silos in three rows and five columns in a grain storage project. The specific procedure was as follows: 1) A feasible optimization scheme was proposed for the ambient vibration test of grain group silos using structural vibration and finite element method (FEM), together with the structural and load symmetry in the actual engineering condition. 2) The measuring points were drawn in the corner silo (No. 11) and the side silo (No. 12), and then the point elevation and orientation were all listed in the tables. The acceleration signals of measuring points were obtained after the test. The least square, five-point three-smoothing, and digital filtering were then used to efficiently process the measured data. 3) The mode shapes of grain group silos were derived using control theory and motion equation of vibration via the acceleration data and transformation matrix. The first four mode shapes and frequencies were calculated to draw for the corner silo (No. 11) and the side silo (No. 12). The results demonstrated that the mode shapes were all the same. In the first four mode frequencies, the calculated values were 2.28, 3.45, 6.37 and 8.26 Hz, respectively, and the simulated values were 2.35, 3.56, 6.31 and 8.16 Hz with an error of 3.07%, 3.19%, 0.94%, and 1.21%, respectively. In the vibration responses of the corner silo (No. 11) and the side silo (No. 12), the first mode shapes of the two silos were all along the short axis direction of the whole grain silos with the same shear deformation and the same amplitude, indicating that there was little effect of adjacent silos on the first vibration response. The second mode shapes of two silos were all along the long axis direction of whole grain silos with the same shear deformation but a different amplitude. The constraint effect among the corner silo (No. 11) and the adjacent silos was weaker than that of the side silo (No. 12) and the adjacent silos. Therefore, the vibration amplitude of the former was larger than that of the latter. The third mode shapes of two silos were torsion shapes around the center of grain group silos, while, the rotational amplitude of the measuring point in the short-axis direction was greater than that in the long-axis direction. The fourth mode shapes of the two silos were significantly different, due to different interactions among the corner silo (No. 11) and the adjacent silos and that of the side silo (No. 12) and the adjacent silos. Bending mode shapes of the measuring points of the corner silo (No. 11) near the side silo, and the amplitudes were relatively small, but the other points were mainly shear or flexural shear mode shapes, and the amplitudes were relatively larger. The reason was that three adjacent silos constrained the side silo (No. 12) to the small amplitudes. Bend-shear mode shapes were found in the measuring points near the adjacent silos, but the points of the middle column were mainly shear mode shapes. Each silo in the grain group silos represented different interactions with the adjacent silos at the measuring positions, indicating a significant impact on the second order and above modes. A seismic design of grain group silos can be expected to divide into several parts for better materials cost-saving, according to the shape and amplitude of vibration mode.

grain; silos; vibration; finite element method; ambient vibration test

2020-11-09

2021-03-19

国家自然科学基金资助项目（51808511）；2019 年度河南省高等学校青年骨干教师培养计划项目（2019GGJS173）；河南省2018年科技发展计划项目（182102110288）；河南省高等学校重点科研项目（19A560026）

张大英，博士，副教授，研究方向为粮仓结构动力问题计算、测试与分析。Email：daying803@126.com

10.11975/j.issn.1002-6819.2021.07.033

TU317+.2

A

1002-6819(2021)-07-0268-10

张大英，张帅枫，孙庆珍，等. 粮食群仓的环境振动测试和角仓边仓振动响应分析[J]. 农业工程学报，2021，37(7)：268-277. doi：10.11975/j.issn.1002-6819.2021.07.033 http://www.tcsae.org

Zhang Daying, Zhang Shuaifeng, Sun Qingzhen, et al. Ambient vibration test of grain group silos and vibration response analysis of the corner and side silos[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(7): 268-277. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2021.07.033 http://www.tcsae.org