基于可靠性可信性分析的云制造服务组合优化

李永湘，姚锡凡，刘 敏

(1.贵州工程应用技术学院 机械工程学院，贵州 毕节 551700；2.华南理工大学 机械与汽车工程学院，广东 广州 510640)

0 引言

中国自2001年加入世界贸易组织(WTO)，到2018年，GDP增长了7倍。17年间，中国制造融入世界制造产业链中，已发展成为世界第一制造大国。中国的发展再次证明开放、合作、创新更有利于经济和制造业的发展，制造全球化、服务化、智能化已成为发展趋势。5G网络技术具有高速度、高可靠、低延时等特点，促进万物互联得以广泛应用，人与人、物与物、人与物之间的通讯速度与质量远超4G技术，这种高速移动通信网络技术与制造装备、检测仪器、物流工具等深度融合，驱动着制造业的发展革新，也使制造业转型过程中存在的一些问题暴露出来，突出体现为制造实体和服务的可信性与可靠性由于2019年美国禁止华为事件而提升到国家决策的高度。2019年底发现的新冠肺炎病毒疫情加剧了世界经济震荡，严重影响着各经济实体的可靠性和信誉，制造企业的生存和发展受到威胁。云制造[1]是一种适应新时代制造业发展转型的面向服务的制造模式，为应对多样化消费需求和日益缩短的产品市场化周期问题提供了解决方案。云计算、虚拟化、服务化技术奠定了云制造基础，物联网技术、通信技术、现代物流技术的发展促进了其应用，5G网络的建设与实施可极大提高无线通信速度，从而进一步推进云制造的应用深度和广度。云制造克服了单个企业在资源、能力、信息等方面的局限性，通过对制造资源和制造能力的虚拟化与服务化，借助云制造服务平台实现分布式制造资源的集中管理[2-4]，为分布式用户提供定制化服务，有助于制造企业和行业克服当前面临的困难。

单个云制造服务往往难以满足用户的多样化需求。为解决用户复杂的制造需求，需要选择多个细粒度的简单云制造服务组合成粗粒度的复杂云服务，供用户按需访问，付费使用云服务所映射的分布式制造资源。云制造服务组合优化是云制造的关键技术之一，是云制造平台服务管理的重要组成部分。云制造服务组合模型构建及其求解算法决定了所求服务组合方案性能的优劣，影响着用户制造任务可否顺利完成、服务质量和制造资源的使用效率与收益，已成为云制造研究领域的一个热点问题。

云制造服务组合优化具有多目标、非线性、不确定性等特点，许多学者都致力于解决这一NP难题[5]。他们主要以生产成本、执行时间、利润等作为优化参数研究了服务组合建模和优化算法，但较少考虑服务可靠性、服务信誉、组合协同性等非功能性服务质量参数在服务组合中的影响。云制造的实现是一个需要多个分布式制造资源共同参与的协作过程。每一个云制造服务执行主体都处于一定的自然环境和社会关系中，不是一个理想化的“刚体”。在制造过程中，云制造服务之间进行不同的数据交换、信息传输和物料运输。它们在整个制造生命周期中相互约束、协作和竞争。云制造服务与制造任务的关系，云制造服务之间的关系，以及云制造服务执行主体之间的关系，直接影响到服务组合执行制造任务的成败和效率。美国制造的中兴事件和华为事件已经证明，深度融入全球产业链的制造企业，在选择组合云服务时有必要将服务可信性、可靠性同制造费用、时间等一起作为衡量云制造服务组合方案优劣的参考指标，为云制造服务用户提供更可信、更可靠、高效的优质服务。在云制造环境下，产品制造需要云制造服务执行主体的协同参与，涉及云制造服务提供者、运营者、客户等，涉及自然的与社会的两方面影响因素。云制造服务的可靠程度、制造过程中云制造服务组合的协同程度、云制造服务的可信程度和服务组合的复杂程度对产品制造任务的完成有着重要影响。因此，云制造服务组合在满足产品交付时间和制造成本要求的同时，有必要以服务可靠度、组合协同度、服务可信度和组合复杂度为参数建模，优化云制造服务组合。

本文研究云制造服务组合中多种影响因素的数学模型和服务组合优化算法。研究中服务组合的基本原则是，根据客户制造需求分解产生的各个制造任务必须分配给一个或多个云服务去执行；求得的最优云制造服务组合方案应有最优的综合性能，即尽可能高的服务可靠度、组合协同度和服务可信度，尽可能小的组合复杂度、交付时间和制造成本。本文主要研究了云制造服务组合的可靠性、可信性分析和云熵粒子群优化算法，主要贡献如下：①提出一种适用于云制造服务组合的云熵粒子群优化算法；②建立了基于服务可靠度、组合协同度、服务可信度、组合复杂度等多个影响因素的云制造服务组合优化模型；③给出一个应用实例，验证所提出优化模型和求解算法的有效性。

1 文献综述

近年来，许多学者采用遗传算法、蜂群算法、粒子群优化算法等方法对云服务组合的建模与优化进行了研究，本文总结了以往学者的研究方法，仔细挑选了与本研究最相关的文献，并将已有的此类研究分为三组。

(1)研究了有关服务可靠性和服务可信性问题。THIRI等[6]为现代虚拟服务网络提出一个独立于服务的、用户观点的可靠性分析指标，根据用户感知实际值对故障影响程度进行了量化。ANDERSON等[7]提出了基于布朗运动的公共汽车服务可靠性数学模型。KHALID等[8]研究了城市公交服务时空网络约束轨道数据模型及服务可靠性评估。CHENG等[9]提出一种商用空调负荷可靠性评估算法，建立了描述空调能源供应服务可靠性的指标体系。CHIU等[10]研究了考虑回溯、服务水平约束、随机故障和报废的制造系统最优运行时间数学模型和优化方法。游静等[11]研究了一种考虑信任可靠度的分布式动态信任管理模型(Distributed Dynamic Trust Management based on Trust Reliability, DDTM-TR)。曹步清等[12]研究了一种基于用户使用历史与信誉评价的Web应用程序接口(Web Application Programming Interface, Web API)服务推荐方法。李嘉等[13]用网络服务数据传输时延和分组丢失率表征网络性能可信度的指标，给出了可信度指标的网络安全测试下网络服务数据传输可信度评估方法。曹继承等[14]通过计算用户可信度对用户进行聚类分析，协同过滤数据，改善Web服务推荐质量。宫清勃等[15]根据客观服务质量(Quality of Service, QoS)属性数据及请求者评分数据，运用差值诱导法评估历史评价信息的可信性。

(2)研究了制造任务分解、资源分配、服务匹配和服务组合。RAILEANU等[16]提出了在能耗与产品调度、资源配置相结合的情况下，基于云的高可用性生产管理系统的设计方法。THEKINEN等[17]将云环境中的资源配置定义为二方匹配问题，从个体合理性、稳定性、策略证明性、一致性、单调性和帕累托效率等方面将二方匹配机制划分为延迟接受(Deferred Acceptance, DA)、顶部交易周期(Top Trading Cycle, TTC)、库恩—芒克雷斯(Kuhn-Munkres, KM)和先到先服务(First Come First Service, FCFS)四种主要类型。TAO等[18]设计了一个基于超网络的云制造服务供需匹配模拟器，可以比较服务匹配结果和调度算法性能。BRANT等[19]研究了云条件下电化学沉积法制备微金属添加剂。基于沉积分辨率对水平沉积参数进行了优化，并将制造数据保存在云中，供用户按需使用。NAMJOO等[20]利用基于资源的理论和决策试行与评价实验室(Decision Making Trial and Evaluation Laboratory, DEMATEL)方法，解决了云制造中复合服务弹性维度与属性之间的因果关系问题。SHENG等[21]研究了智能匹配引擎与云制造服务的匹配过程多样性、异质性和多重约束，建立了基于服务本体语言的云制造服务智能搜索引擎。ZHANG等[22]将云制造服务分配问题分解为增强的拉格朗日协调模型，并采用松耦合分布式方法进行求解。ZHANG等[23]研究了具有容量约束的聚合资源服务分配问题，提出一种改进的遗传算法来搜索最优匹配结果，以达到最小的总成本和时间。ZHANG等[24]提出了分布式制造资源配置并行优化的扩展教学优化算法。

(3)研究了服务质量评价和优化算法。LANG等[25]通过Delphi对云服务质量属性的研究，将服务功能、合法性、服务协议、地理位置和灵活性确定为云服务选择的最高服务质量标准。以云环境下的板料加工为例，以最小成本和最大利润为优化目标，考虑多个子因素，HELO等[26]研究了一种新的云生产计划与控制优化方法，提出一种基于云的动态优化模型，并开发了基于优化算法的调度原型系统。SOUZA等[27]研究了混合雾云场景下的分布式服务配置策略，提出了并发服务执行方案，提高了服务响应时间。YAN等[28]研究了智能制造环境下云机器人的相关技术，包括云机器人网络服务质量的自适应调整机制、云机器人的计算负载分配机制和基于云平台的群学习。LI等[29]研究了服务匹配度、组合和谐度和云熵，提出一种云熵增强遗传算法来解决云制造服务组合多目标优化问题。ZHOU等[30]通过引入食物源干扰协同机制、多样性维护策略和新的计算资源分配方案，改进了人工蜂群算法，解决了复杂云制造中的多目标服务组合和选择优化问题。YANG等[31]提出一种跨多制造云的动态服务选择方法，该方法利用物联网对服务执行的实时感知能力、大数据对制造云服务的知识提取能力以及事件驱动的动态服务选择优化来处理干扰，从用户和服务市场出发，不断调整服务选择。LU等[32]研究了云制造环境中基于知识的服务组合和自适应资源规划，提出一种基于制造云中限制性规则集和资源可用性信息的服务组合方法，以快速地为服务请求分配资源。CHEN等[33]提出一种基于QoS的Web服务组合多目标优化算法，以QoS性能为优化目标，解决了基于QoS的Web服务组合多目标优化模型。HUANG等[34]将遗传算法与粒子群优化相结合，提出一种基于教与学的混合遗传粒子群优化算法。算法中引入一种学习机制，使遗传算法的后代能够从双记忆学习中学习精英染色体特征，在遗传算法模块和粒子群优化模块的两个子群中搜索求解并交换信息。LI等[35]研究了面向自主的云制造服务组合和优化选择，提出一种基于波动性分析的模糊软决策方法。QUE等[36]提出一种新的面向云的制造者—用户模型，解决了制造服务组合的优化选择问题，建立了一个具有4个关键服务质量感知指标(即时间、可靠性、成本和能力)的综合数学评价模型，并采用信息熵免疫遗传算法求解。WANG等[37]研究了基于紧急任务感知的云制造服务组合质量多目标优化问题，提出一种合成与重组两阶段优化算法。ZHANG等[38]研究了一种基于扩展授粉算法的模糊QoS感知制造服务组合方法。XU等[39]提出一种基于多数据的汽车车身设计全局优化算法。采用基于图形处理单元的通用计算技术和混合并行计算方法，提高了求解效率。ZHAO等[40]提出一种基于自适应选择进化算子的SPA2算法来解决多目标优化问题。在进化过程中，算法根据算子的贡献自适应地选择模拟二元交叉算子、多项式变异算子和微分进化算子。HUANG等[41]将制造业云服务按需供应模型划分为按需供应、按需组合、按需设计和按需研究4个子模型，建立了描述个性化产品制造成本和响应时间之间优化机制的二维时空优化模型。PAN[42]设计了一个考虑网络延迟和能耗的多目标光网络无线移动云服务模型，使用多目标水滴算法寻找次优解，并应用NSGA Ⅱ密度设计方法改进多目标水滴算法的种群多样性。HU等[43]针对云制造资源的模糊分类问题，提出一种融合遗传算法、模拟退火算法和模糊C均值聚类算法的混合算法。郭星等[44]研究了一种烟花粒子群优化算法来求解Web服务组合优化问题。陆湘鹏等[45]在研究服务组合中，根据早期多样性修补机制向初始粒子中添加了少量通过局部优选策略生成的粒子来改进粒子群优化算法。

以上研究见证了云制造近几年的飞速发展，然而，上述研究没有从社会与自然两方面综合分析影响云制造服务质量的各种因素与关系，也很少同时考虑服务可信性和可靠性对云制造服务组合性能的作用机制。

2 云制造服务组合数学建模

2.1 服务组合问题描述

2.2 执行时间和执行费用计算

缩短生产时间和降低生产成本是企业经营的两个基本原则，以此来实现利润最大化目标。在云制造服务组合研究领域，服务执行时间和执行费用是云制造服务组合方案性能评价的重要指标。根据云制造环境下制造资源的特点，本文定义了服务执行时间和执行费用。

(1)执行时间(ET) 是云制造服务对制造任务的响应时间。由于云制造服务涉及线上和线下两种因素，其执行时间比普通Web服务要长。此外，物流时间对异构云制造环境的影响往往成为整个制造过程的瓶颈。因此，有必要考虑物流时间对服务执行情况的影响。综上所述，执行时间的值等于云制造服务的加工时间、辅助工作所需的时间(如设备维护、工件夹紧等)和服务执行过程中物料运输所消耗的时间之和，即

ET=Tprocessing+Tauxiliary+Tlogistics。

(1)

式中：ET为执行时间，Tprocessing为加工时间，Tauxiliary为辅助时间，Tlogistics为物流时间。

(2)执行费用(EC) 客户按需使用云制造服务所支付的费用。执行费用的大小等于服务提供商确定的云制造服务费用、服务执行中的物料运输费和云平台收取的第三方服务费之和，即

EC=Cservice+Clogistics+Cplatform。

(2)

式中：EC为执行费用；Cservice为云制造服务费用；Clogistics为物流费用；Cplatform为云平台服务费。

云制造服务组合的类型包括顺序组合、并行组合、选择组合和循环组合，如表1所示。在顺序组合中，根据服务组合中的顺序依次执行不同的服务，组合中的两个服务S1和S2构成一个有序的串行链，服务S2只能在服务S1执行后才能执行。在并行组合中，两个服务S1和S2同时执行，Fork是并行组合中服务操作的开始跃迁，Join是结束跃迁。只有当S1和S2都执行完时，才能触发结束跃迁Join。在选择组合中，选择S1和S2中的一个服务来执行，只要所选择的服务被成功执行完，选择组合就执行结束。Decision是选择组合服务操作的开始跃迁，Merge是选择组合服务操作的结束跃迁。循环组合中服务S1被重复执行，Cycle是循环运算符，Cycle(k){S1}表示服务S1被重复执行k次。不同组合模式下，云制造服务组合的执行时间和执行费用不同，如表1所示。

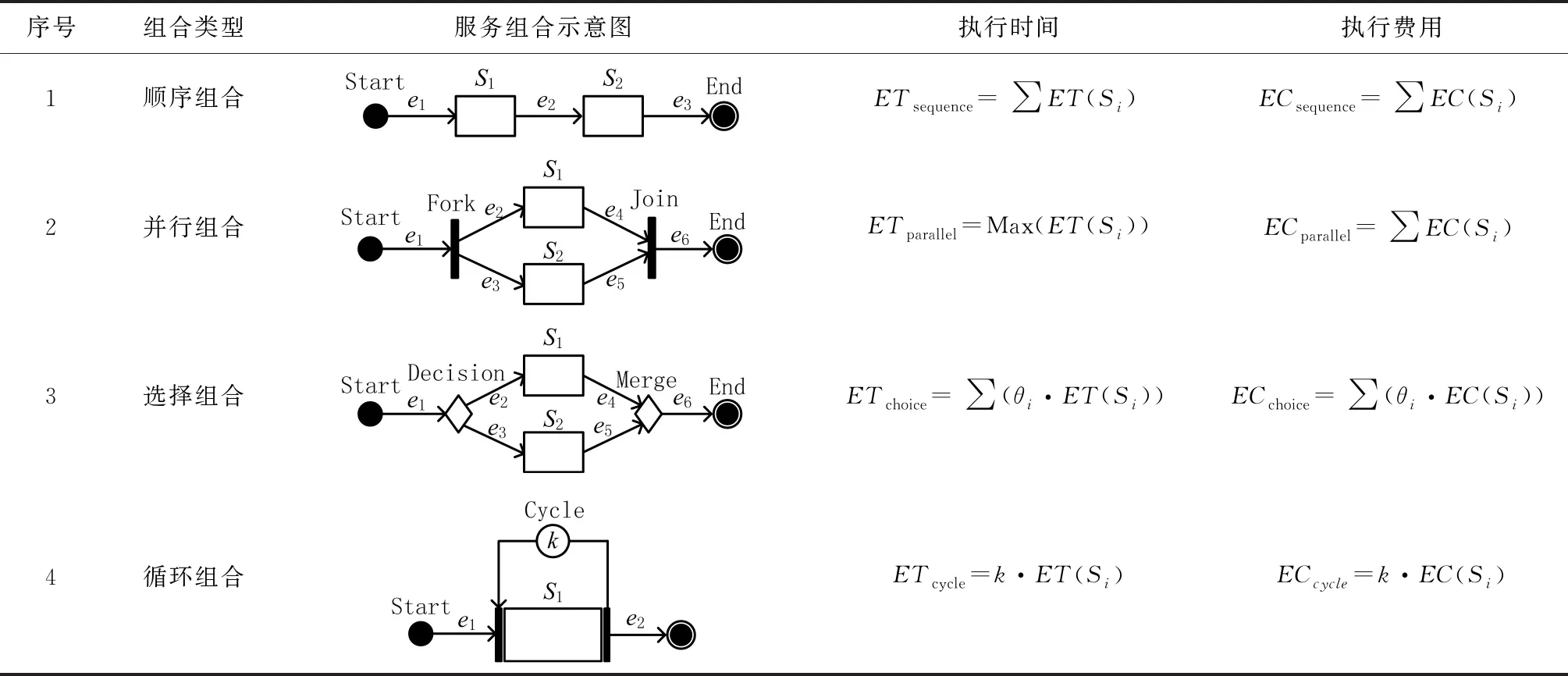
表1 不同类型服务组合的执行时间和执行费用计算

根据服务执行时间和执行费用筛选候选云服务是云制造服务组合中的一项重要工作。然而，仅根据这两个指标筛选候选云服务是不够的。为了充分反映候选云制造服务和服务组合的性能与服务质量，本文将在服务可靠性、可信性分析基础上，将执行时间、执行费用、服务可靠度、组合复杂度、服务可信度和组合协同度作为服务组合的六个质量评价标准，研究云制造服务组合模型构建、算法改进和案例分析。

2.3 服务可靠性分析

服务可靠性主要用来反映云制造中各种客观性、自然性因素对服务质量与服务组合性能的影响，例如制造资源与用户之间的距离、制造设备工作状态、技术水平、功能匹配、工序要求、服务组合复杂程度等。本文通过服务可靠度和组合复杂度来描述这些客观性、自然性因素对服务质量与服务组合性能的影响，定量化表达服务可靠性。

2.3.1 服务可靠度建模

服务可靠度(Service Reliability, SR)是衡量云制造服务与所分配的制造任务之间匹配程度的定量指标。服务可靠度反映了云服务与制造任务之间请求—响应的功能匹配关系。影响服务匹配度的主要因素是制造资源的闲置状况、设备状态、技术水平、功能匹配、工序要求、综合制造能力、云制造服务执行类似制造任务的累计次数、云制造服务的活跃度、云制造服务映射的制造资源与服务对象之间的距离等。根据不同因素的特点，影响服务可靠度的因素可以概括为功能因素、状态因素和距离因素。

(1)功能因素

功能因素(Function Factor，FF)是指根据过去一段时间内执行类似制造任务的云制造服务的累计次数、服务执行率、过去一段时间内服务活跃性和设备性能，来评估云制造服务完成制造任务的技术能力水平。功能因素FFij表示第i个云服务完成第j个制造任务的技术能力度量，1≤i≤N，1≤j≤m。FFij的取值区间为[0，1]。设备性能越好，服务活跃性和执行率越高，累计执行任务次数越多，则功能因素FFij取值越大；反之，FFij取值越小。服务与任务之间的功能匹配完全不符，则FFij取值为0。N个云服务完成制造任务的技术能力可用N×m功能因素矩阵表示，即FF=(FFij)N×m。

(2)状态因素

云制造的突出贡献之一就是激活闲置的制造资源。制造资源闲置率是指未使用于制造任务的可用制造资源数量与制造资源总量的比值。根据云制造服务映射的制造资源闲置率，可以评估云制造服务承接和完成制造任务的期望程度，称为状态因素(State Factor，SF)。SFij表示第i个云服务承接和完成第j个制造任务的客观状态度量，1≤i≤N,1≤j≤m，SFij∈[0，1]。云制造服务映射的制造资源闲置率越高，接受制造任务的期望程度越高，状态因素SFij取值越大；反之，SFij取值越小。通过计算制造资源的闲置率，得到状态因素的值，从而建立状态因素矩阵SF=(SFij)N×m。

(3)距离因素

由于执行过程中离线因素的影响，云制造服务比普通的Web服务更为复杂。空间距离往往成为云制造服务执行过程中的一个制约因素。一般来说，较小的空间距离有利于云制造服务的执行，而较大的空间距离不利于云制造服务的执行。引入距离因素(Distance Factor，DF)来描述云制造服务映射的制造资源与服务用户之间的相对距离对云制造服务执行的影响程度。DFij表示第i个云制造服务映射的制造资源与第j个服务用户之间的距离因子，1≤i≤N，1≤j≤m。相对距离越小，距离因素DFij取值越大；反之，DFij取值越小。例如，如果云制造资源与云服务用户之间的距离为1 000 km，则DFij=0.2；如果距离为100 km，则DFij=0.7；如果距离小于1 km，则DFij=1；同理，也可以得到其他相应的距离因素取值。

综上所述，服务可靠度矩阵可以根据功能因素FFij、状态因素SFij和距离因素DFij计算如下：

SR=

(3)

式中，SRij表示第i个云制造服务对第j个制造任务之间的服务可靠度；SRij=α1×FFij+α2×SFij+α3×DFij，1≤i≤N，1≤j≤m；α1、α2和α3是对应影响因素的权重系数。由于各影响因素对服务可靠度的重要程度不同，3个影响因素可赋予不同的权重系数。3个影响因素的权重系数之和等于1，即α1+α2+α3=1，有助于计算服务可靠度和评估3个影响因素的重要性。

2.3.2 组合复杂度建模

组合复杂度(Composition Complexity, CC)也是衡量服务可靠性的一个重要指标。简单有序的云制造服务组合对于成功完成制造任务具有更大的确定性，服务可靠性较好。复杂无序的云制造服务组合中，执行制造任务时出错的概率较高，成功完成制造任务的确定性较小，服务可靠性较差。熵源于热力学研究，自信息论创立以来有了长足的发展，得到科学界广泛地认可和重视。在云制造活动中，零件第一道工序开始工作节点时间作为零件加工的开始时间，零件最后一道工序完成工作节点时间作为零件加工的结束时间。云制造服务第一次运行的起始节点时间作为云制造服务的起始时间，最后一次运行的结束节点时间作为云制造服务的结束时间。不同的云制造服务在执行制造任务时有不同的连续工作时间、维护时间和物流时间。云制造服务一次完成制造任务的过程复杂度明显比将其分为多个阶段完成的过程复杂度低。云制造服务组合的复杂性和有序性的量化程度可以用云熵(CE)来计算。第i个云制造服务完成相应制造任务的云熵计算如下[29]：

(4)

式中：CEi是第i个云制造服务的云熵;STij是第i个云制造服务在第j个状态下的持续时间;TTi是第i个云制造服务完成相应制造任务的总时间;Qi是第i个云制造服务完成制造任务的状态总数目。云制造服务组合复杂度等于服务组合方案中所有云制造服务的云熵之和，即总云熵，其计算如式(5)所示。总云熵越小，服务组合复杂度越小，云制造服务组合越有序、越简单，服务可靠性越好。总云熵越大，服务组合复杂度越大，云制造服务组合就越无序和复杂，服务可靠性越差。

(5)

式中：N是服务组合方案中的云制造服务总数目;CC是云制造服务组合方案的复杂度，用于度量服务组合的复杂性;CC越小，云服务制造组合的复杂性越小，可靠性越高，成功完成制造任务的概率越大。

2.4 服务可信性分析

服务可信性主要用来反映云制造中各种主观性、社会性因素对服务质量与服务组合性能的影响，例如服务信誉、沟通交流水平、制造实体之间的社会关系等。本文通过服务可信度和组合协同度来描述这些主观性、社会性因素对服务质量与服务组合性能的影响，定量化表达服务可信性。

2.4.1 服务可信度建模

服务可信度(Service Credibility, SC)是针对云制造服务、服务组合、服务提供者、服务使用者、云服务平台在某一时间段内发生的服务交易行为所形成的全局评价。服务可信度可从云服务平台对云制造服务的评分、失信记录、推荐记录、对云制造服务的访问次数方面得到体现，采用服务评分、诚信值和访问量进行计算。

(1)服务评分

所有云服务用户使用完云制造服务后可在云制造服务平台上为该云制造服务评分，用户所给评分(User Score, US)的取值区间为[0,5]，云制造服务平台根据所有用户评分计算出该云制造服务评分值，其服务评分(Service Score, SS)计算公式如下：

(6)

式中：SSi表示用户对第i个云制造服务的标准化平均评分，即服务评分；USh,i表示第h个用户对第i个云制造服务的评分，即用户评分；Li表示评价第i个云制造服务的用户总数量。

(2)诚信值

所有云服务用户使用完云制造服务后可在云制造服务平台上为该云制造服务的诚信水平进行反馈。一个云服务用户可在失信记录框中标记云制造服务为失信，或在推荐记录框中推荐该云制造服务。云制造服务平台根据云制造服务的失信记录(Dishonest Record, DR)和推荐记录(Recommendation Record, RR)计算其诚信值(Credit Value, CV)，具体公式如下：

(7)

式中：CVi表示第i个云制造服务的诚信值；RRi表示第i个云制造服务的推荐记录数量；DRi表示第i个云制造服务的失信记录数量。推荐记录数量越大、失信记录数量越小，云制造服务的诚信值越大；反之，云制造服务的诚信值越小。

(3)访问率

一般情况下，云制造服务的可信度越高，越受云服务用户欢迎，用户再次付费使用和推荐该云制造服务的概率更高，访问该云制造服务的用户数量也会越大。因此，本文采用访问率(Visit Rate, VR)来作为云制造服务可信度的一个衡量指标，其计算公式如下：

(8)

式中:VRi表示第i个云制造服务的访问率;VNi表示第i个云制造服务的访问次数;VNmax表示与第i个云制造服务同类型的所有服务中具有最大访问率的云制造服务的访问次数。

综上所述，服务可信度可由服务评分、诚信值、访问率3个方面计算如下：

SCij=β1×SSij+β2×CVij+β3×VRij。

(9)

式中：SCij表示第i个云制造服务对于第j个制造任务的服务可信度，1≤i≤N，1≤j≤m；β1、β2和β3是对应影响因素的权重系数。由于各影响因素对服务可信度的重要程度不同，3个影响因素可赋予不同的权重系数。3个影响因素的权重系数之和等于1，即β1+β2+β3=1，有助于计算服务可信度和评估三个影响因素的重要性。

2.4.2 组合协同度建模

组合协同度(Composition Synergy, CS)是衡量服务可信性的另一个重要指标。组合协同度表示为完成复杂制造任务而组合在一起的云制造服务之间的协作程度。组合协同度反映了服务组合中两个云制造服务之间的协同关系。在服务组合中，云制造服务之间的信息交换越方便，物料运输越顺畅，协同完成制造任务的时间越短，则云制造服务之间的组合协同度越高；反之，组合协同度越低。由于组合协同度低，云制造服务之间的信息交换和物料运输存在严重障碍，会延误产品交付时间，增加执行费用。云制造服务之间的组合协同度直接反映在执行时间上。通过计算云制造服务完成制造任务所需的时间，可以评估组合协同度。例如，用于完成制造任务Ji和Jj的云制造服务Si和Sj之间的组合协同度可计算如下：

(10)

式中：Ti是云制造服务Si独立完成制造任务Ji所花费的时间；Tj是云服务Sj独立完成制造任务Jj所花费的时间；Tij是两个云制造服务Si和Sj协同完成两个制造任务Ji和Jj所花费的总时间。复杂制造任务分解出的各子任务之间的关系对其总执行时间有很大的影响。制造子任务之间主要存在并行、顺序和交互耦合关系。计算由非耦合制造子任务组成的复杂制造任务的总执行时间相对容易。然而，具有交互耦合关系的复杂制造任务的总完成时间计算却相当复杂。不同情况下的总执行时间Tij计算公式如下：

Tij=

(11)

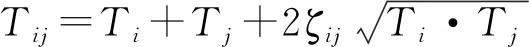
因此，云制造服务的组合协同度矩阵构建如下：

CS=

(12)

式中CSij表示云制造服务组合中第i个云制造服务与第j个云制造服务的组合协同度。

2.5 服务组合多目标优化模型

云制造服务组合的最终目标是选择和组合最合适的云服务，以完成云服务用户的所有制造任务。由此产生的服务组合方案应满足执行时间和执行费用的约束，使云制造服务组合具有最高的服务可靠度、服务可信度和组合协同度，最小的组合复杂度、执行时间和执行费用。云制造服务组合是一个多目标优化问题，其数学模型构建如下：

(13)

(14)

(15)

(16)

minY5=minET=min(max(ET1,ET2,

ET3,…,ETm-1,ETm))，

(17)

(18)

s.t.

max(ET1,ET2,ET3,…,

ETm-1,ETm)≤ET0，

(19)

(20)

(21)

(22)

其中：wi表示第i个云制造服务的单位时间费用;ECj表示第j个制造任务的执行费用。式(13)～(18)是目标函数，其中式(13)表示求总服务可靠度最大值，式(14)表示求总服务可信度最大值，式(15)表示求总组合协同度最大值。式(16)～式(18)分别表示求服务组合的总组合复杂度最小值、执行时间最小值和执行费用最小值。式(19)～式(21)为约束条件，其中：式(19)规定制造任务的最大执行时间不得超过临界时间ET0;式(20)规定制造任务的总执行费用不能超过临界费用EC0;式(21)规定每个制造任务必须分配给一个或多个云服务去执行。

综上所述，在云制造服务组合问题建模方面，本文工作和现有工作的本质区别体现在两方面：

(1)在参数选择方面 本文选择服务可靠度、服务可信度、组合协同度、组合复杂度、执行时间和执行费用6个参数作为QoS指标进行服务组合优选建模，考虑了社会因素和自然因素、人的因素和物的因素对服务组合综合性能的影响，可更全面地评价服务组合QoS。制造实体和制造各环节要素的服务可靠度和服务可信度对云制造的成功实施具有至关重要的作用，尤其是在2019年美国制造的中兴事件和华为事件之后，它们已成为云制造用户、企业、运营商不得不考虑的因素。2019年底开始发现的新冠肺炎病毒(COVID-19)疫情已经扩散到全球，严重威胁着全人类的健康和生命，各国抗击新冠肺炎病毒疫情需要生产或购买大量的呼吸机、体外膜肺氧合器(Extra Corporeal Membrane Oxygenation, ECMO)、口罩等医疗物资。医用材料和医用设备零部件很难由一家企业全部拥有。医疗设备制造企业需要基于云服务在全球范围内采购原材料和零部件，需要综合考虑服务可靠度、组合复杂性、服务可信度、组合协同性、执行时间和执行成本，因为差的服务可靠度和服务可信度会使合作关系不稳定、物流拥挤和信息流堵塞，阻碍产品的正常生产和交付，直接影响企业的生产和生存以及各国抗击新冠肺炎病毒疫情的有效性。当前欧美各国相互拦截医疗物资等，信誉和可靠性受到严重考验。云制造在全球抗击新冠肺炎病毒疫情中发挥着重要作用，充分调动了全球医疗资源，支持和方便了全球医用原材料、零部件采购，呼吸机、ECMO、口罩等的制造，医疗物资的分配等，基于可靠度和可信度的服务组合优选促进了全球合作抗击新冠肺炎病毒疫情。

(2)在建模方面 本文对服务可靠度和服务可信度的数学建模与现有工作不同。对于服务可靠度问题，本文从制造资源的闲置状况、设备状态、技术水平、功能匹配、综合制造能力、执行任务次数、服务活跃度、空间距离等方面来权衡服务可靠性水平，从功能因素、状态因素和距离因素方面量化计算服务可靠度。对于服务可信度问题，本文从云服务平台对云制造服务的评分、失信记录、推荐记录、对云制造服务的访问次数方面来权衡服务信誉情况，采用服务评分、诚信值和访问量计算服务可信度，考量了服务提供者、服务使用者、云服务平台等云制造服务主体的作用，对服务诚信方面的定性问题进行了定量化描述。本文所建模型的服务可靠度和服务可信度评价更富有数学逻辑性，对服务组合综合性能的评价更全面科学。

3 熵增强粒子群优化算法

云制造服务组合问题是一个多目标协同优化的NP难题。传统的粒子群优化算法容易过早陷入局部极值，难以适应复杂的非线性优化问题。因此，其优化质量有待提高。为了改进传统粒子群优化算法的惯性系数和加速度系数，平衡算法的全局搜索能力和局部开发能力，本文提出一种熵增强粒子群优化(Entropy Enhanced Particle Swarm Optimization, EEPSO)算法，以求解云制造服务组合数学模型最优解。算法流程如图2所示。

3.1 粒子编码方法

采用整数编码方法建立粒子位置矢量与服务组合方案之间的映射关系。在云制造环境中，如果一个多重需求的复杂制造任务分解为m个子任务，每个子任务分配给一个候选云服务去执行，则复杂制造任务所使用的服务组合由m个单一制造资源云服务组合而成。从而一个云制造服务组合可表示为m维粒子。粒子维数ParDim=m，粒子的第j维表示复杂制造任务的第j个子任务Jj。任务Jj对应一个云服务集合Sj，集合Sj中包含着任务Jj的多个候选云服务。第j维的值表示任务Jj所选择的候选云服务的编号。假设粒子群由R个粒子组成，则第i个粒子的位置和速度可以用m维向量表示如下：

xi=(xi,1,xi,2,xi,3,…,xi,m),i=1,2,3,…,R,

(23)

vi=(vi,1,vi,2,vi,3,…,vi,m),i=1,2,3,…,R。

(24)

式中：xi,j和vi,j分别表示第i个粒子的第j维的位置和速度。粒子的位置xi,j表示在服务组合过程中任务Jj所选择的候选云服务的编号。图3展示了粒子与服务组合之间的对应关系。对于多个复杂制造任务，可把它们视为同一超复杂制造任务下的多个子任务，将多个复杂制造任务分别分解后得到更基本的子任务，再依据上述方法进行粒子编码。

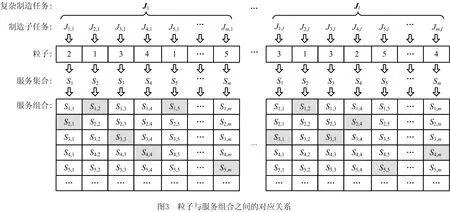
BPi和BGi分别代表第i个粒子的历史最优位置(即个体极值)和整个粒子群的全局最优位置(即全局极值)。它们都可以用m维向量表示，如下所示：

BPi=(BPi,1,BPi,2,BPi,3,…,BPi,m),

i=1,2,3,…,R,

(25)

BG=(BG1,BG2,BG3,…,BGm)。

(26)

式中BPi,j表示第i个粒子在第j维中的最佳位置，并表示由制造任务集J=(J1,J2,J3,…,Jm)所选择的最优服务组合。

在算法的第一次迭代中，粒子群中的粒子Pi被随机生成并分配给个体极值BPi，具有最佳适应度值的粒子被分配给全局极值BG。在后续每次迭代中，根据粒子适应度值更新个体极值BPi和全局极值BG。当达到最大迭代次数时，终止算法，得到综合服务质量最优的云制造服务组合。

3.2 速度与位置更新方法

粒子速度与位置更新公式如下：

(27)

(28)

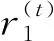
3.3 惯性系数设置

惯性系数是粒子群优化算法中最重要的参数之一。较大的惯性系数可以提高算法的全局搜索能力，避免因陷入局部极值而过早收敛。较小的惯性系数有助于实现一定区域内的精确搜索，提高收敛精度。为避免陷入局部极值，提高粒子的多样性，本文引入正态云模型理论来改进传统粒子群优化算法的惯性系数和加速度系数，建立了非线性惯性系数以平衡粒子群优化算法的全局搜索和局部开发能力。正态云模型是一组遵循正态分布规律、趋势稳定的随机数。它通过4个主要参数进行描述：期望值ExpVal、粒子熵ParEnt、标准差StaDev和超熵HypEnt。改进后的惯性系数计算公式如下：

(29)

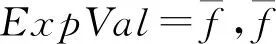
3.4 加速度系数设置

在EEPSO算法的迭代过程中，加速度系数c1和c2确定了粒子自我认知和社会意识对粒子轨迹的影响，反映了粒子群间的信息交换程度，分别代表粒子趋向自身极值和全局极值的加速度权重。加速度系数计算公式如下：

c1=c1,start+(c1,end-c1,start)sin(ψ)，

(30)

c2=c2,start-(c2,start-c2,end)cos(ψ)。

(31)

式中：c1为自加速度系数；c2为全局加速度系数；c1,start和c2,start分别为加速度系数c1和c2的初始值，c1,end和c2,end分别是c1和c2的终止值。加速度系数c1和c2根据式(30)和式(31)设置。在EEPSO算法的初始阶段设置较大的全局加速度系数和较小的自加速度系数，粒子的社会学习能力较强，自我学习能力较弱，从而有利于增强算法全局搜索能力；在EEPSO算法的后期阶段设置较小的全局加速度系数和较大的自加速度系数，粒子的自我学习能力较强，社会学习能力越弱，有利于算法局部精细搜索，高精度收敛至全局最优解。

3.5 适应度函数建立

云制造服务组合的多个目标相互作用，难以用一般的数学方法直接求解。然而，云制造服务组合的目的是一致的，即寻找一种在有限时间、有限费用等条件下正向目标函数值尽可能大、负向目标函数值尽可能小的云制造服务组合方案。EEPSO算法采用加权和方法设计适应度函数。评价服务组合方案效果的标准是所有目标函数值相对偏差的加权和，即加权相对偏差(Weighted Relative Deviation，WRD)。根据云制造服务组合6个目标函数的不同重要性给出权重系数，加权相对偏差计算公式如下：

(32)

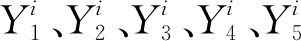
加权相对偏差越小，服务组合方案越好。根据加权相对偏差计算公式，设计EEPSO算法的适应度函数如下：

(33)

式中：f(i)是第i个粒子的适应度函数值；Γ是一个足够大的正数。

3.6 EEPSO算法步骤

EEPSO算法的主要步骤如下：

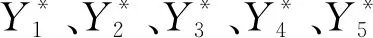
步骤2计算服务可靠度、组合复杂度、服务可信度、组合协同度、执行时间和执行费用。

步骤3计算粒子群中所有粒子的适应度值。

步骤4对每个粒子，将其适应度值f(i)与个体极值f(BPi)进行比较。若f(i)>f(BPi)，则用f(i)替换f(BPi)，用Pi替换BPi。

步骤5对每个粒子，将其适应度值与全局极值f(BG)进行比较。若f(i)>f(BG)，则用f(i)替换f(BG)，用Pi替换BG。

步骤6根据式(29)更新粒子的惯性系数；根据式(30)和式(31)更新粒子的自加速度系数和全局加速度系数；根据式(27)和式(28)更新粒子的速度和位置。

步骤7检查算法的终止条件。若迭代代数达到设定的最大值或满足其他算法结束条件，则停止该算法的迭代操作并输出结果；否则，返回步骤2。

4 应用案例

以基于云制造服务组合完成2台举升装配机器人(Lifting Assembly Robot，LAR)制造任务为例，对本文所提出的服务组合模型和优化算法进行应用。对于众多中小型机器人制造公司而言，企业并不完全具备制造LAR的所有制造资源和能力，且此类产品交货期通常很短，常需要在签约后1个月内交货。企业需要借助云制造平台搜索自身所缺少的制造资源，如图4所示，择优组合云制造服务来完成制造任务，按期交货给客户。云制造能整合机器人制造产业和企业上下游的资源，形成联盟商圈，完成资源协同在线，信息互通，产品服务共享，充分调动闲置制造资源，优化组合云制造服务，实现分布式资源的集中管理使用和集中式订单的分散协同制造，提高机器人制造企业生产效率和经济效益。云制造有助于机器人制造企业紧紧抓住自己的核心业务，而将非核心业务外包出去，在当今网络时代与知识经济时代的背景下，通过云制造实现机器人制造企业的轻资产运营是一种选择和必然。

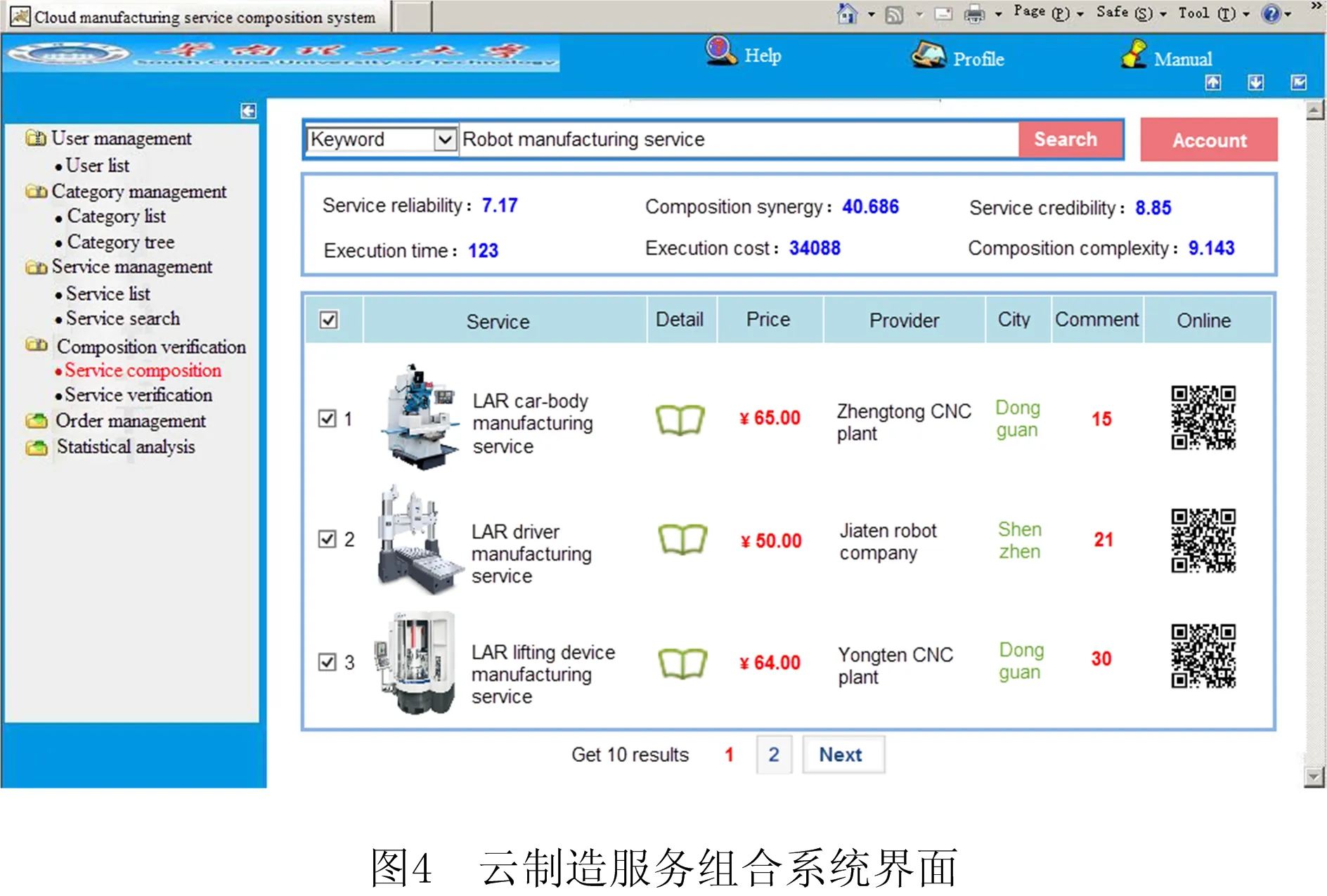
每台LAR制造任务可分为5个子任务：J1车体生产子任务、J2驱动装置生产子任务、J3举升装置生产子任务、J4电控系统生产子任务、J5涂装子任务。5个子任务之间为相互独立关系，J1、J2、J3和J4为并行关系，且都与J5存在顺序关系。根据所提出的EEPSO算法，上述制造任务与云服务的匹配情况如表2所示。制造任务J1，J2，J3，J4和J5的云服务集分别为S1，S2，S3，S4和S5。每个集合中包含的云服务数目分别为3、5、4、2、3。FF,SF和DF分别表示功能因素、状态因素和距离因素。ET,LT、CT和RT分别表示执行时间(单位：小时)、物流时间(单位：小时)、单次连续加工时间(单位：小时)和单次检修时间(单位：小时)。w表示单位执行时间费用(单位：元/小时)，PC表示云平台服务费(单位：元)。取α1=0.4，α2=0.3和α3=0.3，按式(3)计算服务可靠度SR。RR表示推荐记录数，DR表示失信记录数，VN表示访问次数，CV表示服务诚信值，VR表示服务访问率。SS表示服务评分，用户评分如式(34)所示矩阵US中USh,i表示第h个用户对第i个云制造服务的评分。取β1=0.3，β2=0.4和β3=0.3，按式(4)、式(5)和式(12)分别计算云熵CE、组合复杂度CC和服务可信度SC，计算结果如表2所示。

表2 云服务与制造任务的匹配表

(34)

根据式(6)，LAR制造任务的服务组合协同度矩阵可计算如下：

(35)

式中：CS23为5×4矩阵，表示制造任务J2的5个候选云制造服务与制造任务J3的4个候选云制造服务之间的组合协同度。同理可得矩阵CS中其他元素所表示的意义。矩阵CS中所有元素计算如表3所示。

表3 组合协同度计算结果

续表3

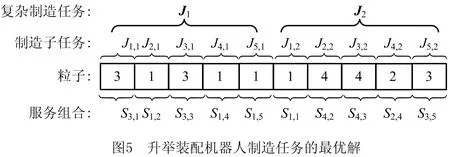
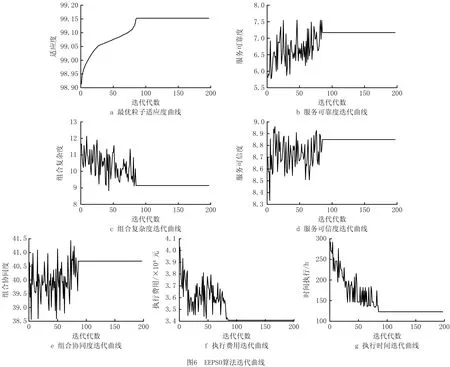
在MATLAB R2015a中编写改进粒子群优化算法程序。最后期限约束ET0=500，执行费用约束EC0=80 000。粒子群大小为ParSiz=50,最大迭代代数为MaxGen=200。取Г=99，6个目标函数的权重系数分别为：δ1=δ3=δ5=δ6=0.2，δ2=δ4=0.1。经过86次迭代，算法收敛，粒子群的最优适应度值为99.153，对应的目标函数值服务可靠度SRsum=7.17，组合复杂度CCsum=9.143，服务可信度SCsum=8.85，组合协同度CSsum=40.686，执行时间ETsum=123小时，执行费用ECsum=34 088元，最优服务组合方案的粒子编码为3131114423。如图5所示，粒子编码表示的意义如下：第1台LAR制造任务J1，1被分配给云服务集S1中的第3个云服务；任务J2,1被分配给云服务集S2中的第1个云服务；任务J3,1被分配给云服务集S3中的第3个云服务；任务J4,1被分配给云服务集S4中的第1个云服务；任务J5，1被分配给云服务集S5中的第1个云服务；第2台LAR制造任务J1,2被分配给云服务集S1中的第1个云服务；任务J2,2被分配给云服务集S2中的第4个云服务；任务J3,2被分配给云服务集S3中的第4个云服务；任务J4,2被分配给云服务集S4中的第2个云服务；任务J5，2被分配给云服务集S5中的第3个云服务。该算法的平均运行时间为18.14 s，其相关参数的迭代曲线如图6所示。粒子群迭代到第86代时趋于稳定。

在最大迭代代数和粒子群大小相同的情况下，分别使用EEPSO算法、传统粒子群优化算法(PSO)[45]、标准遗传算法(Standard Genetic Algorithm，SGA)[46]、云熵遗传算法(Cloud Entropy Genetic Algorithm, CEGA)[29]和混合布谷鸟算法(Hybrid Cuckoo Search and β-Hill Climbing Algorithm, CSBHC)[47]来求解上述同一服务组合优化问题。如图7所示，EEPSO算法在第86代收敛到最优解，PSO算法在第92代收敛，SGA在第141代收敛，CEGA在第95代收敛，CSBHC算法在第94代收敛到最优解。5种算法在同一台配置Intel酷睿i3-3110M CPU、2.4 GHz主频和4 G内存的便携式计算机上运行求解，EEPSO算法用时18.14 s，PSO算法用时19.21 s，SGA用时29.85 s，CEGA用时19.98 s ，CSBHC算法用时19.71 s，如表4所示。以上案例分析和实验结果表明，对于解决云制造服务组合多目标优化问题，EEPSO算法比PSO算法、SGA、CEGA和CSBHC算法具有更快的收敛速度和更短的求解时间。与最小执行时间服务组合

方案(Minimum Execution Time Service Composition, METSC)和最小执行费用服务组合方案(Minimum Execution Cost Service Composition, MECSC)相比较，EEPSO算法求得的服务组合方案具有更高的服务可靠度、服务可信度、组合协同度和更低的组合复杂度。EEPSO算法求得的服务组合方案具有最佳的综合性能，有助于用户从云服务组合综合服务质量角度做出更合理的决策。若在服务组合中只考虑执行成本和执行时间，而不考虑服务可靠度、组合复杂度、服务可信度和组合协同度的影响，则可能导致用户决策失误，对制造任务的执行造成不利影响，这也是METSC和MECSC两种服务组合方案的缺点。由于服务组合方案的服务可靠度和服务可信度都很小，方案中选择的制造服务可能存在技术能力不足、服务质量差、服务信誉差、服务可靠性低、信息流不畅、物流阻塞等问题，会影响产品质量、交货期，甚至影响制造企业的生存，例如，华为等大型跨国制造企业基于云服务全球采购零部件时，需要综合考虑服务可靠度、组合复杂度、服务可信度、组合协同度、执行时间和执行成本，因为低劣的服务可靠性和服务可信性、不稳定的合作关系、拥堵的物流和信息流等会阻碍产品的正常生产，威胁企业的生存。2019年12月开始发现的新冠肺炎病毒疫情对世界上各个经济实体的可靠性和信誉提出了严峻考验，在经济震荡发展和世界复杂多变的当下，云制造有助于制造企业运用有限资产获取最大收益，是所有企业进入21世纪20年代新环境下追求生存和发展的必然之路。

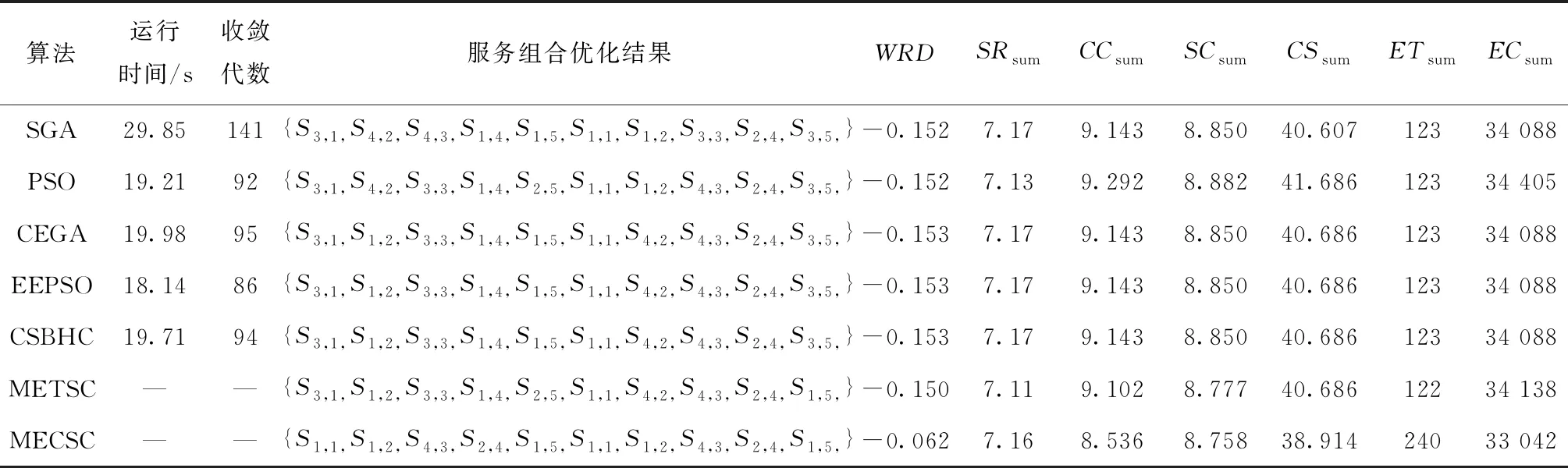
表4 举升装配机器人制造任务服务组合优化结果比较

5 结束语

为了解决不稳定的制造实体可靠性和服务信誉给新时代制造业转型发展带来的影响，本文分析研究了云制造服务可靠性和可信性，探讨了云制造服务组合的多目标优化模型和熵增强粒子群优化算法。主要工作和贡献总结如下：

(1)分析了云制造服务可靠性和可信性，研究了影响云制造服务组合性能的主要因素。将服务可靠度、组合复杂度、服务可信度和组合协同度4个新属性与执行时间和执行费用两个传统属性相结合，综合主观因素与客观因素，自然因素与社会因素，构建了一种新的云制造服务组合服务质量模型，对服务组合综合性能进行了更全面的评价。

(2)建立了云制造服务组合优化数学模型。以服务可靠度、组合复杂度、服务可信度、组合协同度、执行时间和执行费用作为优化目标函数，采用加权和方法构造粒子适应度函数，通过计算加权相对偏差评价服务组合方案性能，为云制造服务组合优化问题提供解决方案。

(3)提出了一种熵增强粒子群优化算法(EEPSO)。通过引入正态云模型，改进了算法的惯性系数和加速度系数。提高了算法初始阶段的全局搜索能力，抑制了算法的过早收敛，形成了更为全面的解空间；并使算法在后期阶段着重于局部精细搜索，提高了寻优精度。

(4)以LAR制造任务为例，验证了所提出的云制造服务组合多目标优化数学模型的有效性和EEPSO算法的可行性。案例研究表明，与SGA、PSO算法、CEGA和CSBHC算法相比较，EEPSO算法对云制造服务组合多目标优化问题具有更高的求解质量和更快的收敛速度。EEPSO算法求得的服务组合方案具有更好的综合性能，有助于云服务用户做出更合理的决策。

云制造等相关技术的发展，促进了新时代制造业的转型发展，激活了各类闲置制造资源，优化了全球制造资源配置。抗击新冠肺炎病毒疫情需要全人类的合作与帮助，云制造技术可以在新冠肺炎病毒的发现、检测、预防和治疗工作中发挥积极作用。在复杂多变的国际环境下，服务可靠度和可信度及EEPSO算法可为云制造平台的服务组合优选和用户决策提供更全面的参考。在后续工作中将注重于云制造服务时变可靠度和时变可信度的研究，提高服务组合优选的动态反应能力。