空间约束下多目标拆卸线平衡问题的改进狼群算法
2021-06-29张则强谢梦柯
蒋 晋,张则强+,谢梦柯,蔡 宁
(1.西南交通大学 机械工程学院,四川 成都 610031;2.轨道交通运维技术与装备四川省重点实验室,四川 成都 610031)
0 引言
现如今,大规模生产导致资源短缺,而对废旧产品随意丢弃、不加以回收利用和缺少无害性处理,给生态环境的可持续发展造成了极大的威胁。因此,为解决环境污染和资源短缺问题,国家出台了大量法律法规引导和鼓励企业注重产品的回收再利用和安全无害化处理。通过对产品进行拆卸达到废旧产品二次利用的目的,获得具有可回收价值的零部件及对环境存在威胁的危害性零部件。通过对有回收价值的零部件进行修复达到合格标准以再次使用,降低企业成本,提高资源利用率;危害性零部件需要经过一系列标准化操作,消除或降低其对环境的危害,达到绿色制造对环境保护的要求。以往的拆卸作业主要由单人单台人工拆解,拆卸效率低下,工人劳动强度高,而拆卸线的建成能很好地提高拆卸效率,实现大规模回收再利用,降低对生态环境的影响。
到目前为止,国内外学者对拆卸线平衡问题(Disassembly Line Balancing Problem,DLBP)[1]进行了研究与讨论,将问题扩展到考虑生产能耗、企业利润、拆卸时间随机性等各方面的平衡优化。例如,HEZER等[2]采用一种基于任务优先关系图,构建最短路径模型间接求解并行拆卸线问题;ALTEKIN等[3]考虑实际拆卸时间会超过节拍时间的情况,提出3种方法减小对拆卸线的影响,建立最大化企业利润的数学模型并求解;REN等[4]提出以利润为导向的不完全拆卸数学模型,并采用引力搜索算法求解。针对DLBP的求解方法,以往主要有启发式算法[1,5-6]、数学规划方法[7]等,主要通过使用权重或约束法将多目标问题转化为单目标问题进行求解,易受决策者主观影响,所得解较为单一,不便于进行多角度决策;其次由于拆卸线平衡问题是NP-完全问题[8],问题规模的扩大会使可行解的数量呈爆发式增长,从中找出最优解决方案的难度也会随之增加。随着国内外学者的不断研究,由于群智能算法[9-12]如蚁群算法[9]、人工蜂群算法[10]、模拟退火算法[11]、粒子群算法[12]等具有鲁棒性强、全局搜索寻优能力强等特点,被广泛应用于DLBP的求解,同时,将群智能算法与Pareto解集思想[13]相结合,能获得多个互不占优的解,便于决策者根据实际情况选用合适的拆卸分配方案。
精益成本管理通过协调各生产要素,以追求利润为最高标准,消除一切无效浪费现象。现有的DLBP中考虑了人因工程、资源利用、能耗约束及工作站空闲时间等问题,缺少对于工作站空间面积约束的相关研究,在实际拆卸生产中经常存在拆卸产品机型种类较多、零部件尺寸范围跨度大、工作站面积大小不一等情况,导致生产车间内布局杂乱,易影响其他物流运输和人员行走,增加物流运输成本,不利于车间的标准化建设与管理,因此有必要研究空间约束下的多目标拆卸线平衡问题(Space constrained Multi-objective Disassembly Line Balancing Problem, SMDLBP)。在制定任务分配方案时,考虑各零部件所需占用的空间大小,使分配到各工作站的任务占用面积之和相对均匀,并以最大所需工作站面积为标准建设拆卸生产线,提高工作站空间利用率及布局的标准化水平。
狼群算法(Wolf Pack Algorithm, WPA)[14]是一种新型群智能算法,将整个狼群划分为头狼、探狼及猛狼3部分,并采用数学函数式抽象表示出游走、召唤、奔袭与围攻等智能行为,通过“胜者为王、强者生存”的规则产生头狼和淘汰弱者,更新种群。算法中,头狼的位置代表当前迭代次数的最优解,其位置会随着探狼、猛狼的变化而变化,而探狼、猛狼则在待寻优空间内自由搜索最优猎物,并交互信息自主决策前进方向,有利于提高算法寻优的效率和质量。算法寻优策略具有多样性,游走行为使得算法全局寻优能力较强,召唤行为平衡了算法的的探索与开采能力,围攻行为加速了算法向全局最优解收敛[15]。与其他算法相比较而言,狼群算法在求解质量和求解速度上更具优势,且其对算法参数设置的敏感性较低,全局优化能力强,鲁棒性强。在实际应用方面,狼群算法主要适用于连续优化问题与组合优化问题,在图像处理[16]、旅行商问题[17]、多目标0-1规划问题[18]、多选择背包问题[19]、卫星导航欺骗干扰识别[20]等各方面均有良好的表现,但在多目标DLBP领域却尚未涉及。
针对上述问题,本文建立了考虑工作站空间约束的多目标数学模型,提出一种离散多目标改进狼群算法(Multi-objective Improved Wolf Pack Algorithm, MIWPA),运用于多目标DLBP求解。在满足优先关系的前提下,采用基于任务编号的编码方式生成各人工狼,同时对算法中的游走行为、召唤行为及围攻行为进行离散化,加强狼群间的信息交流,有利于算法向全局最优点快速靠拢。最后,引入Pareto解集思想和NSGA-Ⅱ拥挤距离机制[21],获得多个目标值较优、多角度综合的解。
1 考虑空间约束的DLBP
1.1 问题描述
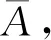
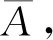

1.2 数学模型
(1)符号说明
n为拆卸任务总数;
K为工作站开启数量的上限值,通常K=n;
CT为拆卸节拍时间,已知量;
i,j为任务编号,i,j∈{1,2,…,n};
h,k为工作站编号,h,k∈{1,2,…,K};
ti为任务i所需标准作业时间,测定可得;
ai为任务i所需占用的工作站面积,测定可得,单位为“1”;
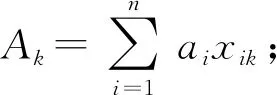

C1为单位面积工作站建设成本,已知量
C2为工作站单位时间附加能耗成本,已知量
C3为零部件单位时间无害化处理成本,已知量
ck为第k个工作站单位时间作业成本;
Tk为工作站k实际作业时间;
RA为优化目标值,表示各工作站实际占地面积的极差值;
TP为优先关系矩阵TP=(pij)n×n,若任务i为任务j的紧前任务,则pij=1;否则pij=0。
(2)决策变量
(3)目标函数
F=min[f1,f2,f3,f4];
(1)
(2)
(3)
(4)
f4=RA。
(5)
(4)约束条件

(6)
(7)
(8)
∀j∈{j|pij=1};
(9)
Sk-1≥Sk,∀k∈{2,3,…,K};
(10)
∀h,k∈{1,2,…,K};
(11)
(12)
(13)
Sk,xik,wk∈{0,1},∀i,∀k。
(14)
模型说明:针对目标函数,式(1)表示优化目标有4个,均为求取其最小极值;式(2)为优化目标f1,计算开启的最小工作站数,为节约成本,应尽可能开启较少的工作站完成拆卸任务;式(3)为优化目标f2,计算工作站空闲时间均衡指标,由于工作站内分配的任务不同,导致站内工人实际工作时间有差异,为了使各工作站劳动强度大致相同,同时为了避免流水线发生堵塞现象,应尽可能使各工作站空闲时间均衡;式(4)为优化目标f3,计算开启工作站以及工作站正常运行过程的总成本,主要由工作站建设成本、开启附加能耗成本、正常运行成本以及危害零部件无害化处理成本4个部分组成,为了实现企业利润最大化,应使总成本尽可能地小;式(5)为优化目标f4,计算工作站实际使用面积极差值,一方面使工作站实际使用面积的变化范围最小,提高各工作站空间利用率,另一方面使各工作站标准化布置面积较小,便于其他物流运输及人员行走,同时降低土地成本。
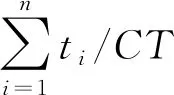
2 求解DLBP的MIWPA
狼群算法是对自然界狼群行为的抽象化数学表示。狼群在寻优空间内捕食猎物,各人工狼可认定为问题的可行解,猎物气味浓度可认定为目标函数适应度值。将整个狼群分为头狼、探狼及猛狼,头狼代表具有最优猎物的狼,即最优解,探狼不断游走搜索确定猎物位置,当搜寻到的猎物气味浓度超过头狼或达到游走阈值T_max时,发起召唤行为,召集猛狼向猎物气味浓度最大的方向奔袭,当所有狼到达攻击距离后,狼群发起围攻行为。狼群遵循自然界“胜者为王、强者生存”的规则,通过不断竞争产生头狼,并剔除种群中的部分较弱个体,完成种群的更新。具体如图2所示。

根据DLBP中拆卸零部件的优先关系和工作站节拍时间约束生成初始化人工狼群,假定人工狼总数为Wolf_num,任务规模大小为T_size,则狼群的捕猎空间即问题的寻优空间为Wolf_num×T_size的欧式空间。
狼群算法具有对参数设置的敏感性较低、鲁棒性强、收敛速度快、求解精度高等优点,将其用于求解离散优化问题,难点在于算法操作过程的离散化以及确保所得解的可行性。在多目标DLBP中,由于各子目标存在一定的对立关系,难以同时达到最优值,而狼群算法中,头狼代表当前最优解,在多目标优化问题中并不是必须存在的,因此本文提出一种改进的离散狼群优化算法应用于求解多目标DLBP,通过去除算法中头狼的作用,对其他算法操作进行离散化,并引入Pareto解集思想和NSGA-Ⅱ拥挤距离机制,获得多个目标值较优、多角度综合的解。
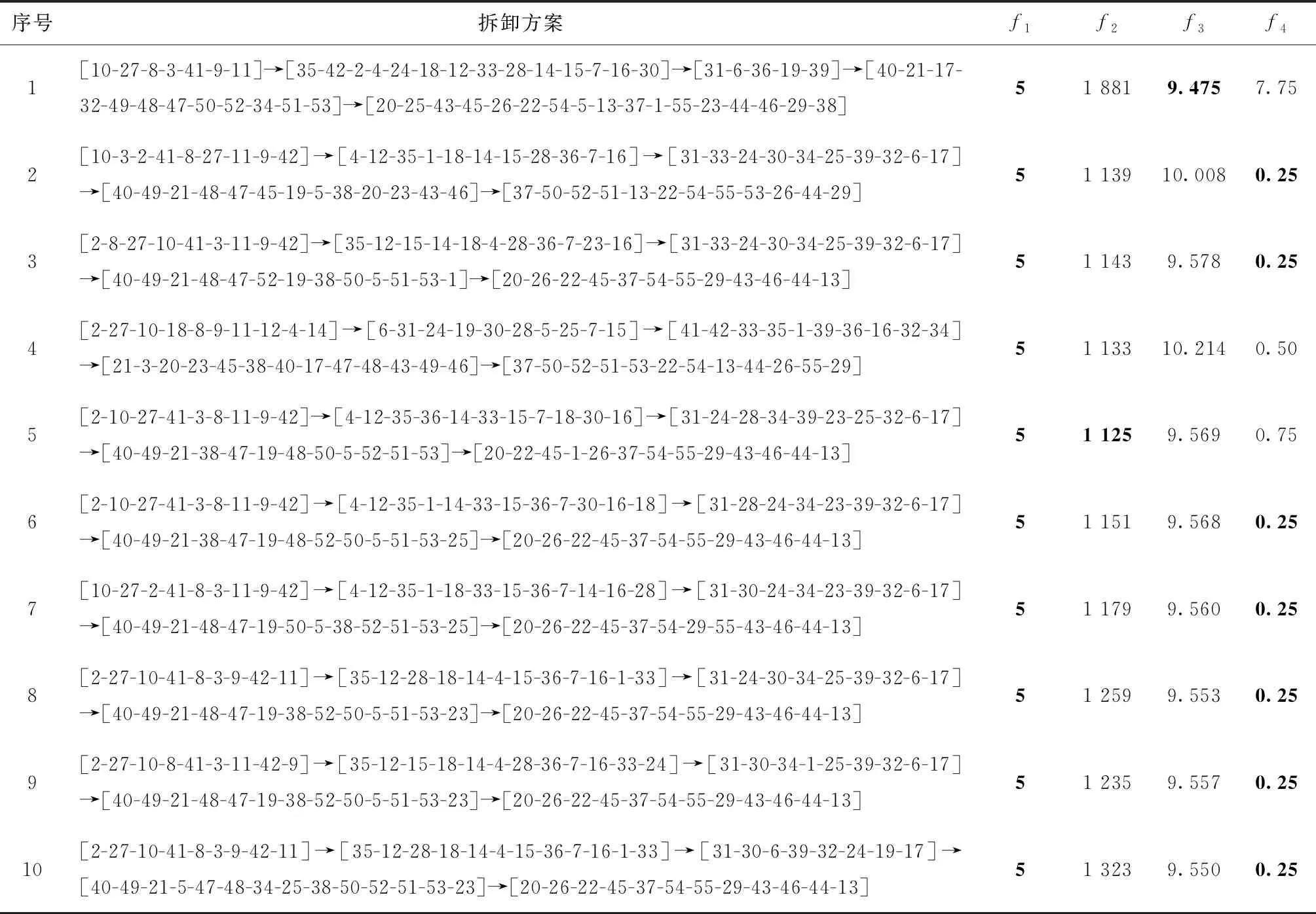
2.1 游走行为
游走行为是挑选初始种群中适应度值较优的人工狼作为探狼S_Wolf,在待寻优空间内搜寻猎物,探狼数量为[Wolf_num/(α+1),Wolf_num/α]间的任意整数,其中α为探狼比例。基于遗传算法中的变异操作,通过随机扰动策略(如式(15))进行探狼游走行为的离散化:
(15)
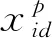
设置游走阈值T_max,初始化游走次数T=1,探狼i选定某一方向进行游走搜索,确定该方向上的拆卸任务编号及其相邻最近的紧前紧后任务位置,以紧前紧后任务间的序列为操作序列,生成与之数量相匹配的随机递增数组,对搜寻方向对应的随机数进行如式(15)所示的扰动计算,然后对随机数组进行重新排序,操作序列相应地改变位置,生成新的序列New_S_Wolf作为探狼游走后的新位置,计算目标函数值作为猎物气味浓度并进行记录,随后探狼返回原位置,重复向h个方向游走,最后选定猎物气味浓度最大的方向前进,随后与其他探狼交互信息,更新自我位置,游走次数T=T+1,探狼继续搜索猎物。当游走次数超过游走阈值T_max,算法转入下一操作。具体实例操作如图3所示。

2.2 召唤行为
召唤行为是狼群中除探狼外的人工狼作为猛狼M_Wolf,向头狼位置快速奔袭靠近,奔袭过程中,猛狼也会感知猎物的气味浓度,当猛狼与头狼距离小于一定值时,算法转入围攻行为。在解决多目标DLBP时,由于去除了头狼的作用而保留其他算法操作,召唤行为具体操作如图4所示。猛狼在探狼发起召唤行为时,采用基于遗传算法交叉操作接收探狼的召唤信息,随后采用变异操作开始奔袭,快速向猎物所在位置靠近,假定全体猛狼奔袭一次即可到达与猎物间的距离小于攻击距离的位置,更新猛狼的位置完成召唤行为。随后狼群向猎物发起围攻,即算法转入执行下一步的围攻行为操作。
2.3 围攻行为
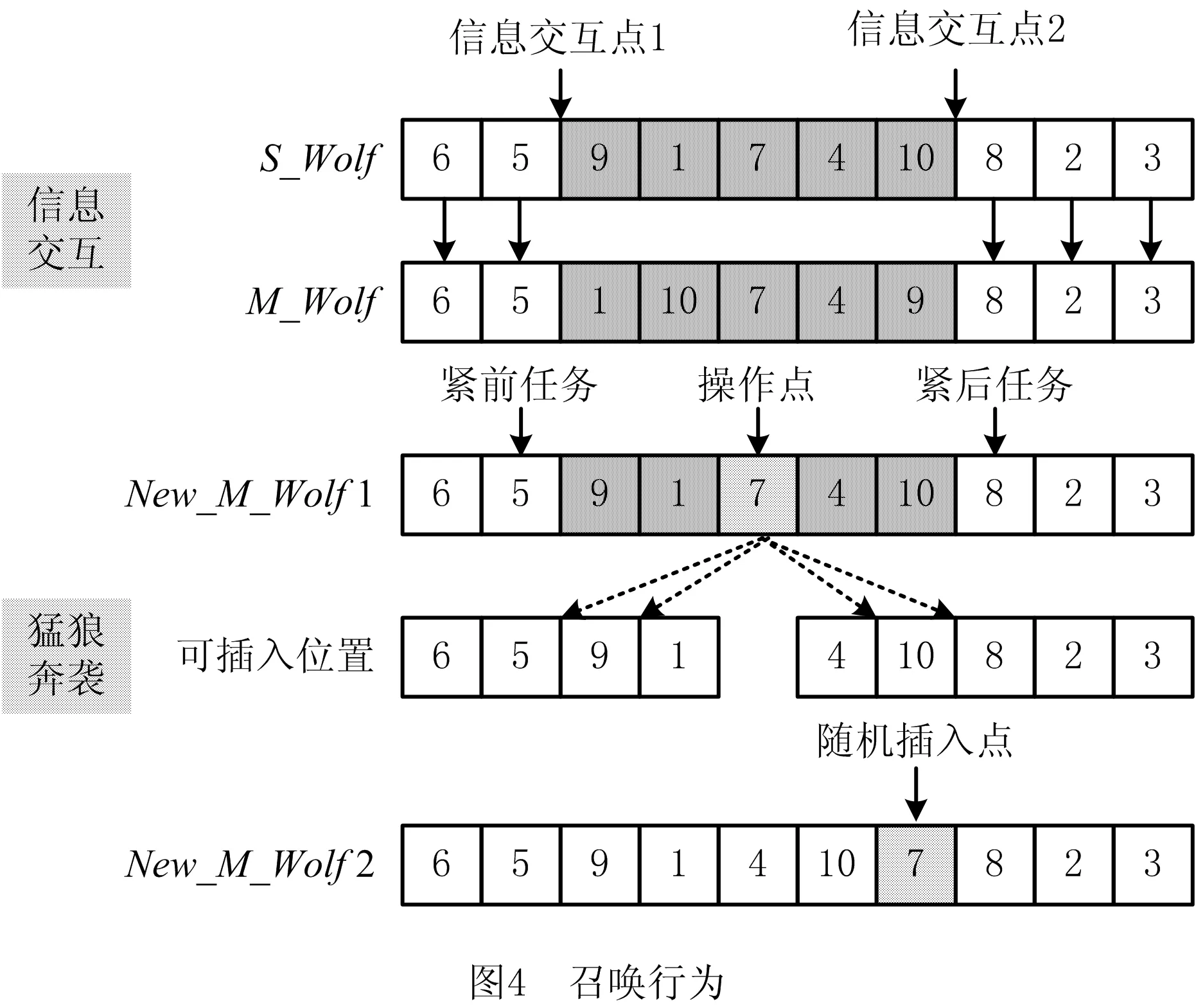
围攻行为是向最优的猎物发起攻击行为。在多目标DLBP中,可将各个目标的适应度值最优的人工狼作为最优猎物Wolf_Best,则可同时存在多个最优猎物,其余狼群分别向各最优目标发起围攻,根据围攻后的猎物气味浓度更新人工狼位置。围攻行为如式(16)所示:
(16)

2.4 “强者生存”更新机制
由于DLBP解集存在多个目标值,不能简单地进行解的优劣性比较,引入Pareto最优解集理论和NSGA-Ⅱ拥挤距离[21]进行解集的评价。
(1)Pareto最优解集理论。任意两个具有Z个子目标的解X1,X2若满足式(17),则称解X1支配X2。
(17)
(18)
狼群算法在算法操作完成后根据“强者生存机制”对狼群进行更新,将适应度值最差的R匹人工狼去除,再随机产生R匹狼加入种群,维持种群规模不变。若Pareto解集的个数大于(Wolf_num-R),则根据拥挤距离排序,去除拥挤距离较小的R匹人工狼,同时随机生成R匹人工狼,最终完成狼群的更新。
2.5 算法流程
MIWPA算法流程如下:
步骤1输入问题信息:优先关系矩阵TP,任务信息矩阵KB(包括零部件危害属性,需求指标,任务拆卸时间与占地面积),问题规模T_size,节拍时间CT。

步骤3初始化种群,设置外部档案Q=∅。
步骤4计算初始种群各人工狼目标值,更新外部档案,划分探狼与猛狼群。
步骤5设置迭代次数gen=1,游走次数T=1。
步骤6探狼根据式(15)在待寻优空间向h个方向游走,感知猎物气味浓度,并与其他探狼交互信息,自主决策前进方向,更新探狼位置。
步骤7判断探狼游走次数T是否达到游走阈值T_max,若T>T_max,则转步骤8,否则游走次数T=T+1,转步骤6。
步骤8探狼发起召唤行为,猛狼接受信息,并开始奔袭。
步骤9奔袭结束后,计算各人工狼感知的猎物气味浓度,随机选取各优化子目标适应度值最优的人工狼位置作为围攻对象,根据式(16)发起围攻行为;
步骤10围攻行为完成后,更新各人工狼位置,计算并记录优化目标函数值,筛选获得Pareto较优解,更新外部档案。
步骤11根据“强者生存”原则更新种群。
步骤12判断算法终止条件:若gen MIWPA算法流程图如图6所示。 在Intel(R)Pentium(R)CPU G645 @2.90 GHz 2.90 GHz处理器,内存为4 GB的计算机硬件配置条件下,通过MATLAB R2016b开发MIWPA程序并运行计算。通过求解P25问题[22],P52问题[13]并与多种算法进行对比,说明MIWPA能应用于多目标优化DLBP中。 表1 P25问题各算法求解结果 由表1对比分析可得:各单目标最优结果分别为:f1=9,f2=9,f3=70,f4=802。现有的5种计算方法只能求解获得最小工作站数量f1及最小负载均衡指标f2的最优值。通过将本文所提MIWPA算法应用于P25问题的求解,获得了10组较优的分配方案,其中各子目标均能求解获得单目标的最优值。从Pareto解集思想角度分析,已有的5种求解方法中,GA的解与RL的解互不占优,PSO的解支配GA的解和PL的解,SA的解支配GA的解与RL的解,VNS的解支配其他4个解,由此可得已有的5种求方法中,VNS的解为非劣解;所提的MIWPA算法求得的10组解中,解6、解7支配除VNS的其他四种方法所求的解,MIWPA所求的其他解与已有的求解方法互不占优。综上所述,MIWPA算法能适用于求解中规模DLBP问题,且能综合平衡各目标要求求解得到较优解。 表2 MIWPA求解P52问题结果 由表2结果可得,MIWPA算法求解大规模问题,得到10组非劣解,计算结果所得工作站平均闲置率FIdle均为0.057 9,平缓率FSmooth的范围为79.17%~99.97%,拆卸成本FCost的范围为124.800~141.132元。将求解结果分别与多目标布谷鸟算法(Multi-objective Discrete Cuckoo search, MDCS)[27]、人工鱼群算法(Artificial Fish Swarm Algorithm, AFSA)[28]、多目标细菌觅食算法(Multi-objective Bacterial Foraging Optimization, MBFO)[29]、改进猫群算法(Improved Cat Swarm Optimization, ICSO)[30]和遗传模拟退火算法(Genetic Algorithm and Simulated Annealing, GASA)[31]进行对比分析,结果如图7所示。与其他5种算法相比,可以看出MIWPA所求解结果更逼近Pareto前沿,所求解分散性较强,目标值更优,说明本文所提算法适用于求解大规模DLBP问题。 为验证本文所提MIWPA算法和数学模型的有效性,现以实际中某打印机为对象制定拆卸线任务分配方案。该打印机有55个拆卸任务,拆卸信息 如表3所示,包括任务拆卸时间t/(s)、危害属性Y(1代表有危害性,0代表无危害性)、零件占地面积a/(单位面积)、单位时间拆卸成本U/(元/s)及紧前任务集合P。 表3 某打印机(P55)拆卸信息表 续表3 综合考虑市场需求和实际拆卸时间,确定节拍时间:CT=150 s。算法参数设置与第3.2节一致,以1.2节所提的模型中的优化目标进行求解计算,将MIWPA算法运行10次,取其中一次较优求解结果如表4所示,表中加粗字体表示的是各个子目标的优化最优值。 表4 MIWPA求解SMDLBP结果 表5 MIWPA求解DLBP结果 通过对比SMDLBP问题和DLBP求解结果可得,所需的工作站均为5个,但考虑空间约束情况下求解获得的f2指标最优的方案5支配DLBP求解的所有方案;成本指标f3最低的方案1与DLBP的所有方案均互不支配;工作站实际使用面积极差值指标f4最优的方案3、6~10不劣于DLBP求解所得的全部方案,方案2和方案4由于额外考虑工作站空间面积约束,寻求各目标的折中平衡点,导致成本过高而劣于DLBP求解中的方案3和方案9,但其单个工作站空间利用率最低分别为95.35%、97.67%,远优于方案3和方案9。SMDLBP结果与DLBP结果对比如图8所示,图8a为求解结果Pareto前沿图示对比,从图中可以看出,SMDLBP所求结果分散性较优,更靠近Pareto前沿,各子目标最优值均优于DLBP所求结果。结合表4、图8a可以看出,当空闲时间均衡指标f2、工作站实际使用面积极差值f4越来越小时,拆卸成本f3会随之逐渐增加,表明f3与f2、f4存在对立关系,难以同时达到最优。图8b为求解结果中各方案工作站实际使用面积极值对比图,结合表4、表5可得,DLBP求解方案中单工作站最小使用面积均为5.75,最大使用面积为15.75;单工作站空间利用率最低为36.51%,空间总利用率最低为67.30%,最高为80%。而考虑空间约束情况下,方案1由于过分追求拆卸成本最小化,而忽略了空闲时间和面积极差值等因素,导致单工作最小使用面积仅为6,最大使用面积为13.75;单工作站空间利用率最低仅为43.64%,空间总利用率最低为77.09%。方案2~10综合考虑各子目标,寻求平衡点,可得单工作站最小使用面积为10.25,最大使用面积为11;单工作站空间利用率最低为93.18%,空间总利用率最低为96.36%,最高为98.60%。 综上所述,考虑空间约束情况下,企业成本、工作站的空间闲置率等各指标总体趋势比不考虑的情况下低,且工作站实际使用面积变化波动小,空间利用率高,便于生产车间的场地布局标准化,降低物流运输成本和土地成本等。 针对拆卸产品机型种类较多的柔性生产车间内零部件尺寸范围跨度大,导致工作站实际面积大小不一,不便于其他物料及人员流动,增加了企业生产成本的实际情况。本文首次在拆卸过程中考虑工作站空间面积约束,建立以最小化工作站数量、空闲时间均衡指标、拆卸成本及工作站面积极差值为优化目标的数学模型。设计开发了一种离散的多目标改进狼群算法,采用基于任务的编码方式生成各人工狼,对游走行为、召唤行为及围攻行为进行离散化,并引入Pareto解集思想和NSGA-Ⅱ拥挤距离机制,获得侧重点不同的多种分配方案。通过P25、P52问题的求解计算,并与现有文献的结果对比分析说明MIWPA求解DLBP问题的适用性和优越性。最后,将所提问题与求解方法应用于实际的某打印机拆卸线平衡问题中,获得10组可行解,并与不考虑空间约束的情况下进行对比,结果显示考虑空间约束下拆卸线占地面积少,成本较低,空间利用率明显提高,证明所提模型和算法的优越性。 在拆卸线设计过程中,不同的布局形式下的空间面积约束存在较大差异,且零部件的质量和形态均存在一定的不确定性,后续可结合U型、并行、双边等布局形式特点对空间约束下随机型拆卸线平衡问题展开深入研究。
3 算法验证
3.1 中规模算例
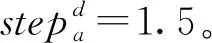
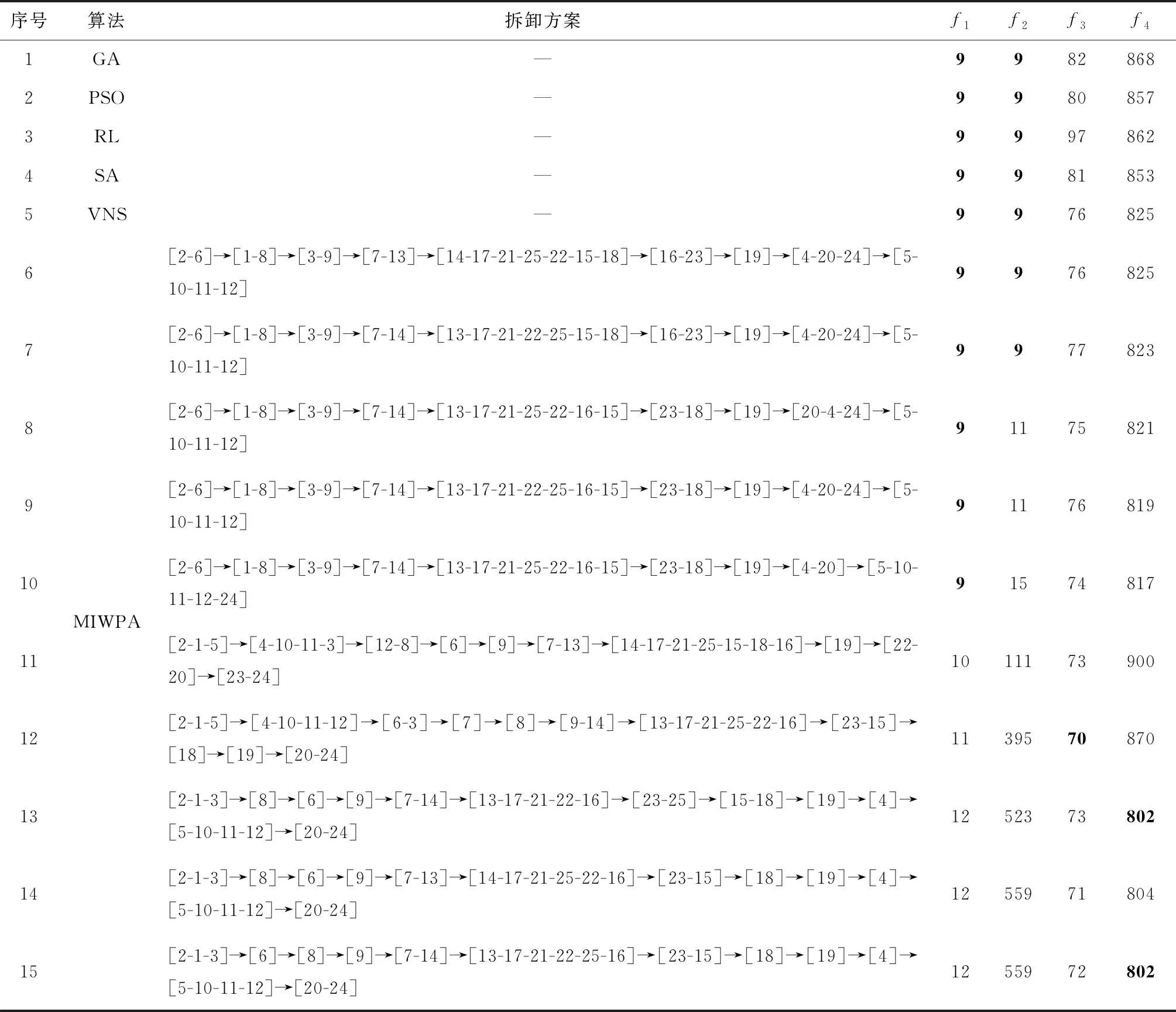
3.2 大规模算例


4 实例应用



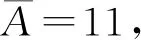


5 结束语
