基于时间递推建模及交叉熵算法求解柔性作业车间调度问题
2021-06-29杨艳华姚立纲
杨艳华,姚立纲
(1.福建江夏学院 工程学院,福建 福州 350108;2.福州大学 机械工程及自动化学院,福建 福州 350116)
0 引言
随着市场全球化和客户需求的日益多样化,多品种小批量的柔性制造方式已成为大量制造企业的主要生产模式。相比传统的车间调度问题,柔性作业车间调度问题(Flexible Job-shop Scheduling Problem, FJSP)的灵活性和复杂性更高,是NP-难问题,传统的数学规划方法和部分枚举法只能在问题规模较小时求得最优解[1]。近年来元启发式算法的发展为FJSP的求解提供了新的技术途径,大量的FJSP的研究论文采用了进化算法(Evolutionary Algorithms, EAs)或多方法混合技术[2]。进化算法框架下的诸多变体如遗传算法(Genetic Algorithm, GA)、分布估计算法(Estimation of Distribution Algorithm, EDA)[3-6]都成功地应用于FJSP的求解。其他元启发式算法,如入侵性杂草优化算法(Invasive Weed Optimization, IWO)[7]、免疫算法(Immunity Algorithm, IA)[8]、灰狼优化算法(Grey Wolf Optimization, GWO)[9]以及禁忌搜索算法(Tabu Search, TS)[10]等也取得了很好的效果。近年来研究文献表明,针对FJSP的研究逐渐由单目标向多目标拓展,但单目标优化的技术依然处于重要位置。研究的主要工作集中在对所使用优化算法的改进上,包括多策略混合算法[11-14]、并行化[4]和加强局部搜索[15],其共同思想是在全局搜索和局部搜索之间权衡。全局搜索注重试探解的多样性和分布广泛性,局部搜索注重收敛性,从而在有限的时间内获得较理想的解。
与元启发式算法不同,交叉熵(Cross Entropy, CE)算法[16-17]是基于概率模型采样生成试探解的全局优化算法,可通过监控分布函数控制生成解的散布,克服一般启发式算法生成试探解的盲目性。通过反馈更新概率分布模型,引导算法在优质解的区域内采样,使算法具有很强的全局搜索能力。然而,CE算法采样的机理源于大数定律,所需样本量大,这使得算法在局部搜索时效率不高,实际运用中多和其他方法结合以提高整体效能,如LI等[18]将CE算法和萤火虫算法两套不同搜索机制进行协同,设计了一种混合交叉熵萤火虫算法(Cross-Entropy Firefly Algorithm, CEFA),用于求解高维函数优化问题。CE算法在求解调度问题方面的研究主要有:SANTOSA等[19]在CE算法的基础上引入遗传算法的交叉变异操作,设计出一种混合交叉熵遗传算法,用于求解零等待作业车间调度问题;WANG等[20]针对炼钢—连铸生产调度问题,以最小化总能耗为优化目标,通过改进交叉熵算法对部分精英个体执行基于交换操作的局部搜索;佘明哲等[21]将CE算法结合自适应变邻域局部搜索,用于求解模糊分布式装配流水线低碳调度问题。当前CE算法的主流应用方式是与其他机理的优化算法或操作结合,发挥各自优势。然而,鲜有研究将CE算法与FJSP在模型层面结合,使得CE算法的潜力未能充分挖掘,多数方案只是将CE算法用于生成较好的初始种群。
本文将研究重点下沉到模型层面,通过对FJSP模型及其可行解的研究,发现已有研究中普遍采用的基于加工序列的解的表示方法不唯一,优化算法计算效率降低。通过对模型和CE算法两方面特点的研究,建立基于甘特图的解的归总表示,并构造两阶段法的计算模型,融入CE算法的计算结构,研究改造后的计算模型对整体算法效能的影响,从而开发实用的优化算法。
1 柔性作业车间调度问题模型
1.1 问题表述
柔性生产车间包括多台机器(柔性制造单元),每台机器具有对多种工件的不同工序进行加工的能力,即机器具有“柔性”。但不同机器进行不同作业的效率不同,如何为待加工工件安排机器、如何为机器的作业排序,使整体效率获得优化,即为柔性作业车间调度问题[1]。柔性作业车间调度问题的数学表述有多种方式,本文采用文献[22]的记号,以最大完工时间最小化为目标。
在m台机器上加工n个工件,每个工件j需要nj道工序,各工序之间遵循工艺约束,工件j的每道工序Oji可由多台具有相似功能的机器加工,可用机器集合设为Sji。若选定其中机器k加工,则将耗用pjik个单位的加工时间。目标是希望所有工序都完成的时间尽可能早,得到优化模型如下:
minCmax=min(max(Cji))。
(1)
s.t.
Cji-Cj(i-1)≥pjikXjik,i=2,3,…,nj,k=1,2,…,m;
(2)
(3)
∑Xjik=1,k∈Sij,∀i,j;
(4)
Xjik∈{0,1};
(5)
Yghji∈{-1,0,1}。
(6)
其中:
j,g为工件号索引,j,g=1,2,…,n;
i,h为工序号索引,i,h=1,2,…,nj;
k为机器号索引,k=1,2,…,m;
Oji为工件j的第i道工序;Cji为工序Oji的完工时间;
Xjik为工序分配机器的决策变量,若工序Oji选择在机器k上加工,则Xjik=1,否则Xjik=0;
Yghji为决定工序先后顺序的决策变量,若工序Ogh为Oji相邻的前一道工序,则Yghji=-1;若工序Ogh为Oji相邻的后一道工序,则Yghji=1,否则Yghji=0;
Sji为工序Oji的可用机器集合Sji⊂{1,2,…,m};
Cmax为调度方案的最大完工时间。
式(1)为目标函数;约束条件(2)反映一个工件必须依从前向后的次序加工各工序,且只有前一工序完成才能加工下一工序;约束条件(3)限定同台机器上不能同时加工两个工件;约束条件(4)限定工序Oij只能在一台机器上独立完成,不能跨机器加工;约束条件(5)和约束条件(6)限定决策变量的取值范围。
1.2 基于时间递推关系的柔性作业车间调度问题模型构建
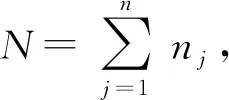
minf(IP,P)。
s.t.
IP满足工序约束;
P满足机器可用约束。
(7)
其中f为目标函数,本文以各工序最大完工时间为目标,有f(IP,P)=Cmax。
设向量st∈RN为加工序列中各工序对应的开始时间,如st(j)表示第j个位置所进行工序的开始时间;相应地,设ct∈RN为加工序列中各工序对应的完成时间。由加工调度的内在机理可知,st(j)取该工序所使用机器的上一次工作完成时间lastmachineT和该工序对应零件上一道工序完成时间lastprocessT的最大值。由此可以得到每一个位置工序完成时间的递推关系:
st(j)=max{lastmachineT,lastprocessT};
(8)
ct(j)=st(j)+q(IP(j),P(IP(j))。
(9)
其中q是矩阵,表示各个工序用不同机器加工所消耗的时间,由最初模型中的pjik演化而来,q(IP(j),P(IP(j))表示j位置的加工对应的工序IP(j)在选择使用机器P(IP(j))时所消耗的时间。只要工作排序满足工序约束,则通过式(8)和式(9)的递推关系,就可以得到整个系列工作的完工时间f(IP,P)=max(ct)。
1.3 解的等价性和归总表示
由式(8)和式(9)的递推关系可知,如果两个相邻位置j和j+1的工序既不是同一个零件的先后工序,又不使用同一台机器加工,则它们二者各自的开始、完成时间不受对方影响,也即若二者交换IP中的顺序,不会影响整套工作的进度安排,两个加工方案对应的甘特图相同。
基于此,定义FJSP可行解的等价关系如下:设[IP,P]是FJSP的一个可行解,若IP(j),IP(j+1)两个工序不是同一个零件的工序,且P(IP(j))≠P(IP(j+1)),则将IP的j与j+1位置上的工序交换,并保持机器排序向量P不变,所得到的新解[IP′,P]也是一个可行解,并称[IP′,P]为[IP,P]的一个相邻对换。进一步,若[IP2,P]可以由[IP1,P]经过有限步相邻对换得到,则称[IP1,P]和[IP2,P]等价。
求解FJSP的元启发式算法的实现方案中,对工序的编码大都采用类似于本文中IP的向量形式,以表示工序优先顺序。这意味着这些算法对可行解的表示同样存在着不唯一性,即不同的编码向量对应本质相同的解,这会导致交叉、变异操作生成等价解,从而误导改进方向,降低算法效率。为解决这一问题,本文提出了等价解归总表示的方式,即通过增加约束条件,使等价解中的某一个作为代表元。归总表示的原则如下:
IP*=argminτ(IP);
s.t.
IP∈S。
(10)
其中:τ(·)表示排列的逆序数,S为等价解集,IP*为等价解的归总表示,它是等价解中逆序数最小的一个。
由式(10)可知,对于采样得到的每个精英样本[IP,P],只要对IP在工序约束下进行减少逆序数的重排,即可得到等价解的归总表示,下面的排序算法给出了一种简单的实现方式。
算法1排序算法。
置j=1,
步骤1若IP(j)>IP(j+1)且满足前述可交换条件,则交换二者位置。
步骤2若j 步骤3当进行至一轮搜索中j=1,2,…,N-1时均未发生工序位置交换,迭代终止。 算法2CE算法。 步骤1给定ρ∈(0,1),单次采样数N,终止参数d,采样分布密度函数f(·;v)和初始抽样分布参数v0,令t=1。 步骤2按照f(·;vt-1)在可行域X中进行采样,生成试探解x1,…,xN,计算相应的函数值。 步骤3对样本函数值排序S(1)≤S(2)≤…≤S(N),并计算相应的1-ρ分位数γt,即 γt=S(⌈(1-ρ)N⌉)。 (11) 步骤4记Nelite=N-⌈(1-ρ)N⌉+1为精英样本数,选取S(⌈(1-ρ)N⌉),S(⌈(1-ρ)N⌉+1),…,S(N)对应的Nelite个样本,对分布密度函数进行更新,更新公式为: (12) 得到的解作为新的vt。 步骤5若对某个t≥d,满足γt=γt-1=…=γt-d,则迭代终止,取值为S(N)的采样点为最优解;否则,置t=t+1,转步骤2。 在实际的优化计算中,vt的更新经常采用平滑化处理,将式(12)的解(命名为wt)与上一次迭代的参数vt-1的加权平均作为更新的参数,即 vt=αwt+(1-α)vt-1。 (13) 其中平滑系数α∈[0,1]。通过平滑化处理,采样分布的系数不会变化过于剧烈,以避免陷入局部最优点。 CE算法的改进版本FACE(fully automated CE),其主要思想是自适应地调整每次的采样数Nt,使之在最小采样数Nmin和最大采样数Nmax之间变动,这样的改进提高了算法的适应性。本文采用改进的FACE模式,以函数值最小化为目标,用于求解FJSP。 根据CE算法的框架,试探解是根据一定的分布函数采样获得,采样的试探解具有广泛的分布性,且可以通过调整分布函数进行重点采样,这使得CE算法具有很强的全局搜索能力。然而,FJSP带有工序约束,不能直接采样。一般处理约束的方法有罚函数法和拒绝抽样,这两种方式都会生成不可行解并进行处理,降低采样效率。本文采用了一种“随机分布筛”的工具,不是筛选采样点,而是对采样分布进行筛选,从而使得生成的采样点都是满足约束的可行解。 设Pr1∈RN×N为用于生成IP的概率分布矩阵,Pr2∈RN×m为用于生成P的概率分布矩阵。Pr1中的元素Pr1(i,j)表示第i个位置选择第j号工序的概率,Pr2中的元素Pr2(i,k)表示第i个位置选择第k号机器的概率。由于同一工件工序的先后关系约束,第i个位置选择的工序号,并不能取自{1,2,…,N}的任何数,而是与之前的选择有关。 引入逻辑向量poslog∈RN,表示当前位置可以选择的工序号 (14) 这样,可利用poslog向量对概率分布进行筛选,去除不该选择的工序的可能性。用MATLAB代码表示如下: pr=Pr1(i,:).*poslog, pr=pr/sum(pr)。 (15) 其中符号“.*”表示对应元素相乘。这样筛选得到的pr就是概率分布向量,可直接根据它生成i位置上的可行解。这里起关键作用的是poslog向量,称为随机分布筛。一旦第i位置上的工序选定,则更新poslog,筛选i+1位置上的生成概率分布。 整个随机生成可行的IP的过程命名为feasiblegenIP,用算法形式表示如下。 算法3feasiblegenIP算法。 输入:初始化概率分布矩阵Pr1,初始poslog。 置i=1, 步骤1筛选生成概率分布pr=Pr1(i,:).*poslog;pr=pr/sum(pr)。 步骤2由pr生成当前工序号,IP(i)。 步骤3更新poslog,poslog+=refresh(poslog)。 步骤4若i=N,停止循环,输出IP;否则,置i=i+1,转步骤1。 对于机器分配向量P,也可用类似方法处理,过程命名为feasiblegenP。通过随机分布筛,求解FJSP的约束优化模型式(7)可转化为无约束优化问题,从而纳入到CE算法框架下求解,该过程命名为CEopt。根据式(15)可知,只要初始采样分布矩阵元素都非零,则poslog只会消除不可行解的可能性,而保留所有可行解的生成可能性。这使得算法有一定的概率生成任何一个可行解,从而保证了试探解散布的广泛性。 CEopt优化的目标函数,以[IP,P]为决策变量,维数是2N,如果能降低决策变量的维数,相当于压缩了可行解集,同样的采样数目在可行域中的分布就更加稠密,从而在随机采样时能以更高的概率取得最优解。基于这样的动机,本文提出了两阶段计算模型:首先对给定的工序顺序IP寻找到最优的机器分配P,相当于确定了二者之间的函数关系 (16) 然后求解以IP为决策变量的N维优化问题 (17) 式(16)可以通过传统优化方法求解,而式(17)采用CE算法。理论上,问题式(16)和式(17)与传统调度问题式(1)的最优解对应的决策是等价的,而问题的维数却减少了一半。 两阶段法实施的关键在于对式(16)问题的高效求解。给定工序顺序后,对每个位置上的工序优选机器,每个位置都有m种选择(如果机器都可用),N个位置共有mN种组合方式。贪婪算法计算量相对较小,虽然不能保证找到最优解,但常用来寻找“不劣解”。其做法是:对第i个位置(相应工序号IP(i))寻找最优的机器,使得该位置对应工序完成时间ct(i)最小,机器号记入P(IP(i))。当i取遍所有位置时,就得到了机器分配P。贪婪算法最大的问题是它的短视性,作为改进,提出半穷举半贪婪算法,算法具体步骤如下: 算法4半穷举半贪婪算法。 步骤1对排序的第1~K个位置,采用穷举法,试探m种机器,共有mK种组合,计算每种组合导致的工序结束时间ct。 步骤2对每一种组合,从i=K+1开始,使用贪婪算法,为余下的N-K个位置寻找机器分配。 该算法是贪婪算法与穷举法的结合,称为“半穷举半贪婪算法”。本文中的两阶段计算模型中,子问题式(16)采用K=1的半穷举半贪婪算法;而子问题式(17)依然采用CE算法。整个两阶段计算过程记为twostage。 本节引入的几个工具和计算模型,是基于FJSP和CE算法特点设计的:随机分布筛解决工序约束条件下的随机采样问题;两阶段计算模型充分利用FJSP机器分配和工序排序表示上的可分离性实现降维,降低CE算法计算负担;半穷举半贪婪算法利用了小规模FJSP的启发式方法的思想。这些改进和等价解的归总表示一起嵌入到CE算法框架中,与FJSP深度融合,具体在下一章阐述。 在保持CEopt的结构框架的前提下,将两阶段计算模型嵌入到生成可行解步骤中,既保持了CEopt按概率收敛的特性,又利用了两阶段计算过程的快速性,得到混合CE优化算法hybridCEopt1。设置算法切换的二维概率分布向量pswitch=[p,1-p],以概率p生成1,以概率1-p生成0,0和1作为切换算法的依据。 算法5hybridCEopt1算法。 给定工件数、各工序数、各工序号矩阵,初始的概率生成矩阵Pr1、Pr2,概率分布筛poslog,算法切换概率分布向量pswitch,采样数ns,置k=1。 步骤1对每个工作位置,利用Pr1和poslog生成ns个可行的加工顺序IP(即执行算法feasiblegenIP)。 步骤2利用pswitch按概率生成算法选择标志flag,若flag=1,转步骤3;否则,转步骤4。 步骤3用步骤1生成的IP求解式(16)问题,得P;并计算函数值f(IP,P)。 步骤4利用Pr2生成ns个可行的机器分配P(即执行算法feasiblegenP),并计算函数值f(IP,P)。 步骤5根据ns个函数值,筛选精英样本,更新概率分布矩阵Pr1和Pr2;poslog恢复为初始值。若满足终止条件,程序终止;否则,置k=k+1,转步骤1。 hybridCEopt1算法保持了CE算法的框架,只是在具体实现中嵌入了第2章中的改进工具。1.3节引入的等价解归总表示的排序算法,在上述步骤1后执行,得到排序后的IP,它将在步骤5中影响概率分布矩阵Pr1的更新,使得生成非归总表示的等价解概率降低,从而在下一次迭代中减少冗余解的生成。4.1节仿真实验中将通过实验对比直观展现排序的影响。 纯随机搜索的CE算法,每一次迭代的样本通过一定概率模型的采样获得,这使得CE算法具有很强的全局搜索能力,但随机采样用于局部搜索计算负荷较大。针对该问题,采用了两项加强措施: (1)用启发式方法找到一些非劣解加入到初始解集合中,加强hybridCEopt1算法的步骤1和步骤4,使得算法启动时就能将采样分布矩阵更新到较好的分布。 (2)利用局部寻优技术,对精英样本进行局部寻优,加强hybridCEopt1算法的步骤5,提高获得最优解的概率。 措施(1)采用类似文献[5]中的初始样本选取方法:①在初始随机采样中选取1/8的样本,固定机器分配P,改造工序顺序IP:随机采用最长加工时间优先(Longest Processing Time, LPT)规则和最多剩余工序优先(Most Operations Remaining, MOR)规则;②在初始随机采样中另外选取1/8的样本,固定工序顺序IP,改造机器分配,将工序分配给工作量最小的机器。将改造后的样本与剩余样本一起用于更新分布。 措施(2)采用文献[6]中搜索算子的思想,分别固定P和IP,搜索更好的IP和P,类似于2.3节中两阶段法。不同的是这里采用随机方法。将精英样本按照优劣排序为X1,X2,…,Xelite,先将下标形如X4i+1,X4i+2的样本用于搜索IP,将形如X4i+3,X4i+4的样本用于搜索P,如有多余的精英就舍弃不用;然后交换搜索次序,再做一次。 搜索IP的方法是:对某两个样本X4i+1,X4i+2,固定P,随机选取某些工件构成集合J,固定X4i+1中非J工件对应工序的位置,其他位置按照X4i+2中J工件的各工序排序,得到新的样本Y4i+2。如果Y4i+2优于X4i+2,则取代X4i+2。交换X4i+1,X4i+2二者地位,再进行一次上述操作。 搜索P的方法是:对某两个样本X4i+3,X4i+4,固定IP,随机选取P向量中的某几个位置J,交换两个样本中P对应位置的分量:P4i+3(j)↔P4i+4(j),j∈J,得到两个新样本Y4i+3和Y4i+4。如果新样本优于原样本,则取而代之。 局部搜索中,样本向量中变动的分量J通过随机方法选取,但优先选取关键路径中的工序位置和机器。通过以上改进的算法命名为hybridCEopt2算法。虽然局部寻优依然采用随机方法,但搜索区域不再是整个解空间,而是精英解集内部各向量之间部分元素交叉互换后的可行解集,计算复杂度并没有提升。 仿真实验在Intel Core i7-8550U CPU、8 GB RAM 计算机的MATLAB R2016环境上进行。仿真实验分为两部分内容:①在CEopt框架下,研究可行解的归总表示对算法收敛速度的影响,以验证模型改进的效果;②检验带局部寻优的混合型算法hybridCEopt2有效性,与其他智能算法比较。 采用KACEM等[25]所提算例,展现采用可行解的归总表示排序对算法计算效率的影响,使用原始框架下的CEopt算法。CEopt算法中的参数为:单次最少采样样本数300,精英样本数50,初始采样分布均采用离散均匀分布,平滑系数0.3。实验分两组进行:①对生成的可行解进行归总表示排序;②直接使用生成的可行解,不排序。每次实验分别使用CEopt迭代200次,记录首次求得最优解的迭代次数、采样数量、求得最优解总次数和总采样数。进行10次实验,求其平均值取整,结果如表1所示。 表1 可行解归总表示排序对CE算法的影响 由实验可知,采用可行解排序处理的算法,首次取得最优解所需迭代次数和采样点都更少,减少20%。值得注意的是:根据表1中“首次获得最优解的迭代次数”和“200次迭代中求得最优解次数”数据,可推算出排序处理后的算法在第27次迭代求得最优解后,每次迭代都取得最优解,说明采样概率分布矩阵也已收敛;而未经排序的算法,在第34次迭代求得最优解后,有21次迭代没有找到最优解。 如图1所示为工序生成概率分布矩阵随迭代的变化情况。选择第1次迭代,第5次迭代、第20次迭代和第50次迭代时的概率分布矩阵,以3维柱状图反映矩阵各元素的取值。在无排序情况下,概率矩阵p变化缓慢,而在有排序的情况下,概率矩阵p收敛迅速,50次迭代后,最低的概率也接近0.7。这说明可行解的归总表示能提高收敛速度。当机器和工序数目更大时,重复解的数量会变得更多,归总表示的作用将更加突出。 值得注意的是,用元启发式算法求解FJSP的方案中,如果工序排列的基因编码也采用向量形式,则也会出现可行解表示不唯一的问题,这将导致一部分交叉、变异操作的无效——仍表示同一个解,从而使算法效率降低。如果采用归总表示,并在交叉、变异操作时避开等价解,则可望提升种群的多样性,提高算法效率。 hybridCEopt2算法是纯随机搜索算法hybridCEopt1通过加强初始样本选择和局部寻优后的改进。为验证其有效性,本文通过两组算例——Kacem1~Kacem5[25]和MK01~MK10[26],与多种FJSP求解算法进行比较。hybridCEopt2算法参数设置为:单次最少采样样本数Nmin=10×工件×机器,单次最多采样样本Nmax=10×Nmin,精英样本数100,初始采样分布都用等概率分布,平滑系数0.2,算法切换概率pswitch=[0.6,0.4],当连续10次迭代单次采样点达到Nmax且最优解没有改善,算法终止。对算例Kacem1~Kacem5,分别进行20次运算,成功率和最优值作为指标列入表2,与文献[6,13,22,27]中不同算法进行比较。hybridCEopt2算法和其他算法一样,求得同等最优值的成功率都达到了100%。 表2 Kacem1~Kacem5算例计算结果 对算例MK01~MK10,CEopt算法和hybridCEopt2算法各进行20次运算,求得最优值列入表3,与文献[6,9,15,22,27]中的算法比较,最后两列括号中数字表示平均的最优值。其中CEopt算法采用纯随机搜索,没有使用本文提出的改进措施。由表3中的结果可看出,除算例MK10外,hybridCEopt2算法求得的最优值能达到其他算法的最优水平;文献[15]的算法利用了关键路径进行精细的邻域搜索,使得对算例MK10表现最好。主要原因在于两种算法的出发点不同:文献[15]的算法是遗传算法和精选的邻域结构下局部搜索的结合,重点在邻域结构的精选;本文的hybridCEopt2算法没有使用精细的局部搜索,是带有局部搜索功能的随机搜索算法,主要为了展现计算模型的改进带来的优势,重点在随机搜索的模型改进,相当于更好地实现文献[15]算法中遗传算法的功能,而没有使用邻域结构搜索。如果将邻域搜索算法用于本文的改进计算模型中,则可望有更好的性能。值得注意的是文献[6]中的两种算法——BEDA(双种群EDA)和单种群EDA,和hybridCEopt2算法同属于基于概率模型的算法。从它们的计算结果来看,hybridCEopt2表现普遍优于EDA,而与BEDA相当:对MK06算例hybridCEopt2较优,而对MK10算例则BEDA较优,对其他算例二者表现持平。原始的CEopt算法除了对MK03算例表现稍好以外,对其余的算例计算结果与hybridCEopt2相比差距都较大,这说明本文提出的模型改进对CE算法性能有明显的提升。表4给出了原始的CEopt算法与hybridCEopt2算法的计算时间,可以看出,尽管hybridCEopt2增加了排序和两阶段计算过程,每一次迭代计算量增加,但是整体效能高于原始的CEopt算法。特别是对MK01、MK02、MK03和MK04算例,hybridCEopt2算法所用时间不到CEopt算法的一半。主要原因是CE型算法采用按照概率分布生成随机数的方式产生样本,MATLAB程序在生成样本时耗时较长,而hybridCEopt2算法的改进措施提高了样本的质量,减少了迭代次数,使因迭代次数减少而导致的计算量的减少量大于每次迭代计算量的增加量,总体效率提高。 表3 MK01~MK10算例计算结果 表4 CEopt与hybridCEopt2计算时间的比较 s 为防止只考虑求得最优值而不考虑所遍历的总体个数的局限性,采用基于总体个数的评价指标[13],以文献[13]中提出的SMGAIWO(自适应变级遗传杂草算法)及其性能对比算法GA(遗传算法)、IWO(遗传杂草算法)作为比较对象,以算例Kacem2进行测试,比较算法性能。结果如表5所示,其中GA、IWO和SMGAIWO算法的计算结果源自于文献[13]。 表5 Kacem2算例的计算结果 续表5 表5数据显示,GA在遍历约360 000个样本后,得到最优解15,最优解质量不如其他算法的最优解14。IWO算法找到最优解14需遍历约360 000个样本,SMGAIWO只需约220 000个样本。而hybridCEopt1算法不做局部搜索,仅需要18 558个样本,hybridCEopt2算法所需样本更少,效率优势明显。图2为hybridCEopt2求解Kacem2所得最优解对应甘特图。 本文提出的算法hybridCEopt2可以简单地看成是全局搜索和局部搜索的结合,改进点主要在全局搜索阶段的CE算法,其主要效果是:在局部搜索之前就生成比一般全局搜索更好的可行解集,既提供了好的初始值,又减轻局部搜索的负担,甚至对某些问题即使不采用局部搜索,也具有很高的效率(如表5)。主要原因是:CE算法根据概率分布生成的试探解具有广泛的分布特性,可行解的归总表示压缩了搜索空间,而半穷举半贪婪算法起到了部分局部搜索的功能,使得采用简单的局部搜索也能取得很好的效果。 通过对FJSP模型的研究发现,传统的工序编码方式存在不唯一性,使得同一套加工方案对应很多可行解,从而直接影响优化算法的求解效率。将FJSP数学模型和CE算法计算模型深度融合,提出了求解FJSP的CEopt算法、hybridCEopt1和hybridCEopt2混合算法,经过仿真实验,得到主要结论如下: (1)基于甘特图的可行解归总表示对使用CE方法求解FJSP的效率提升有显著的作用,表现在采样分布参数和最优解收敛速度的提高。 (2)不同于拒绝抽样和罚函数法,随机分布筛处理约束问题可以避免生成不可行解,从而增加有效采样率,相当于将约束优化问题转化为无约束优化问题,提高CE算法的效率。 (3)使用两阶段计算模型可以降低问题的决策变量维数,提高计算速度。将两阶段计算模型嵌入CE算法框架得到的混合算法hybridCEopt1是有效且高效的,在不特意引入局部搜索的情况下,计算所需样本数量远少于进化算法。 (4)对采样初始样本的启发式改进、引入简单的局部寻优的hybridCEopt2算法,优化能力就能接近使用精细邻域搜索的算法,说明对CE算法的一系列改进可使之生成质量更高的试探解,减轻后续局部搜索的负担。 本文的重点在于改进计算模型,在局部寻优策略方面,没有采用精细的邻域搜索方法,二者融合是今后值得研究的方向。2 交叉熵优化算法
2.1 交叉熵算法简介
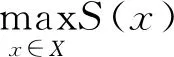
2.2 随机分布筛

2.3 两阶段计算模型

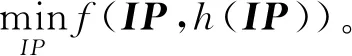
2.4 半穷举半贪婪算法
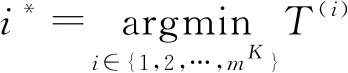
3 混合CE优化算法
3.1 纯随机采样的混合CE优化算法
3.2 局部寻优的混合CE优化算法
4 仿真实验
4.1 模型改进对算法收敛速度的提升作用
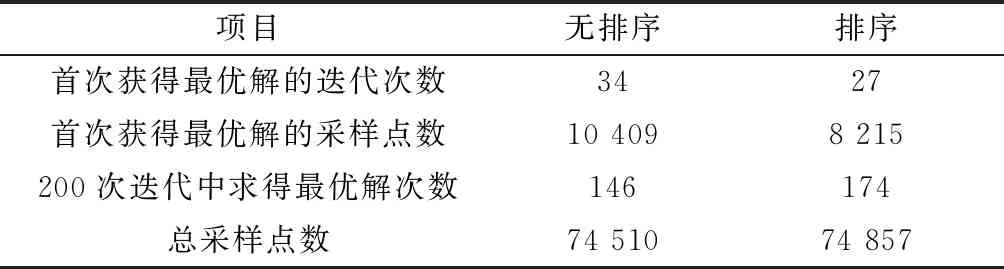
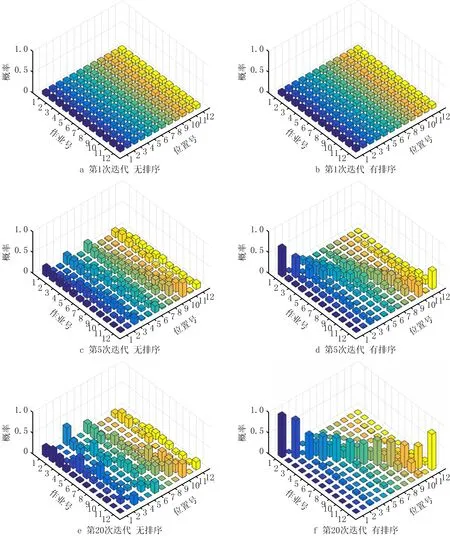
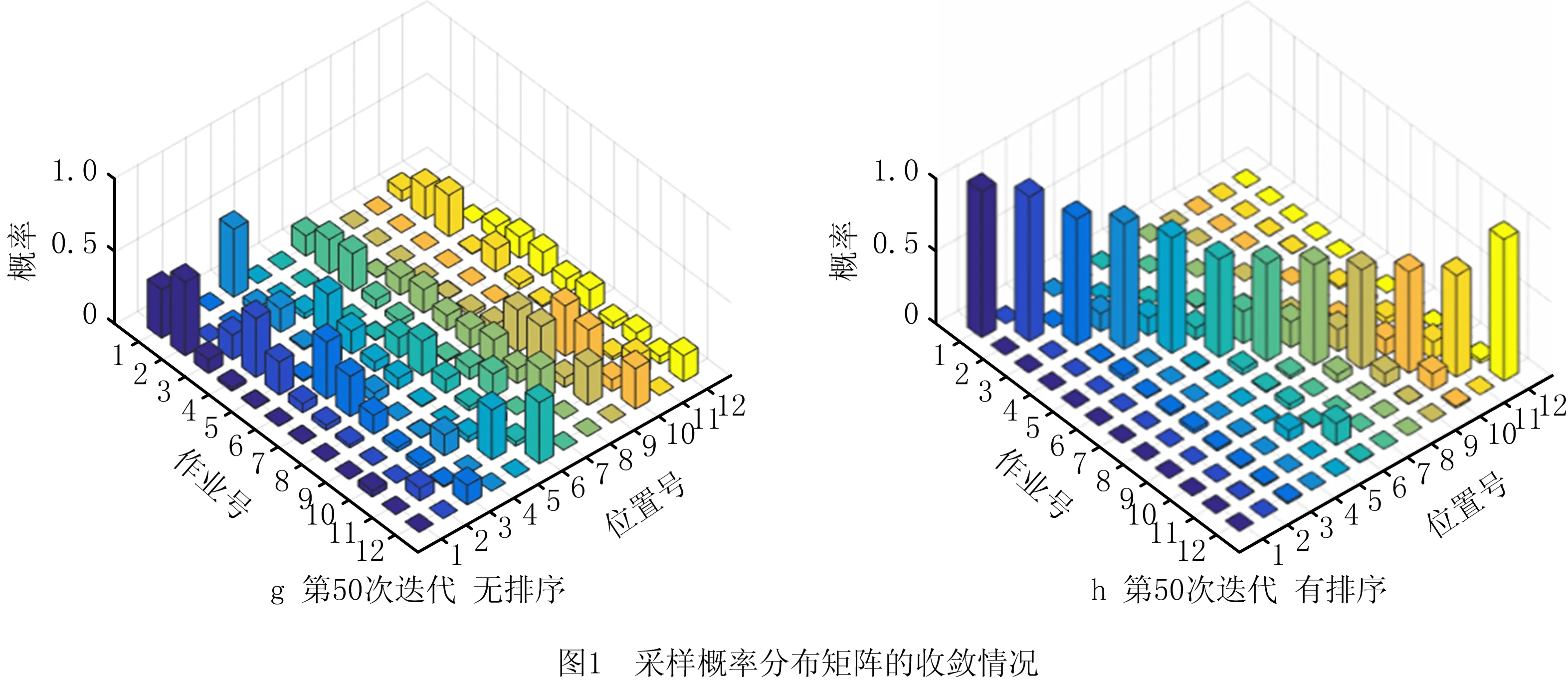
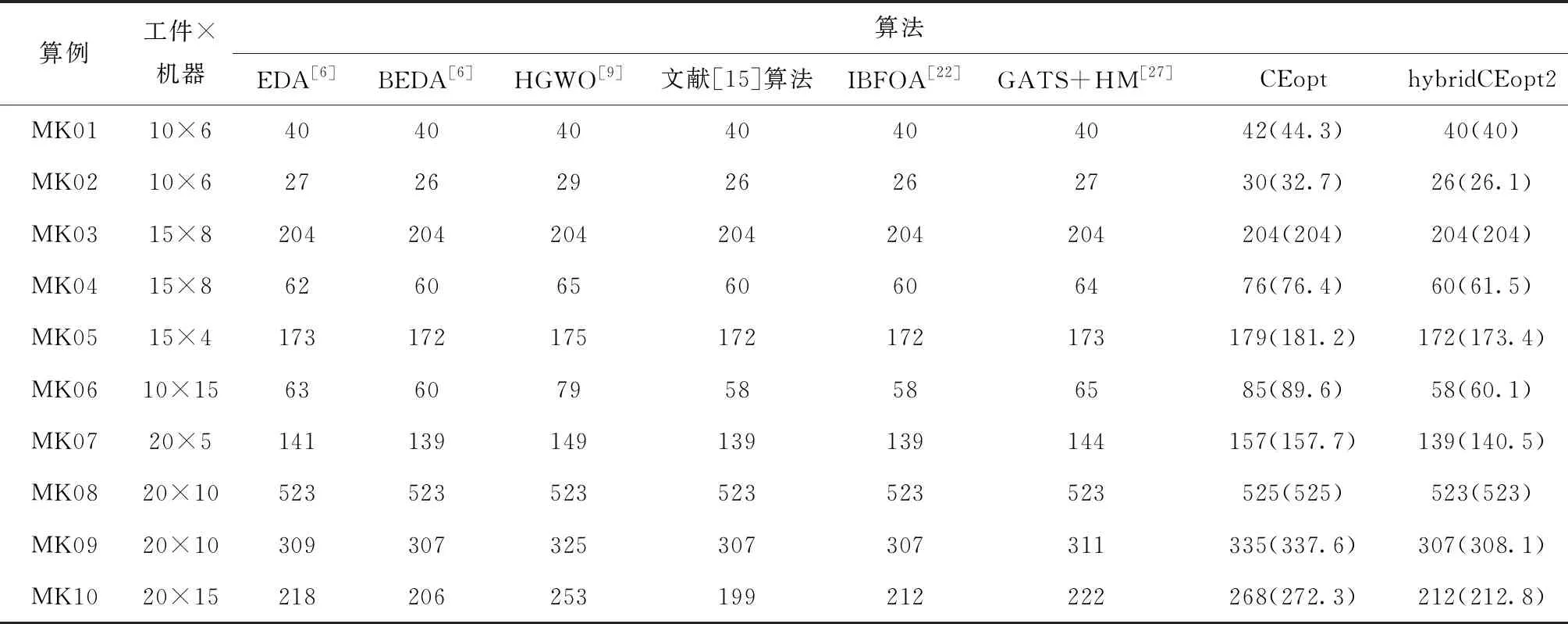
4.2 局部寻优的混合型CE算法hybridCEopt2的有效性
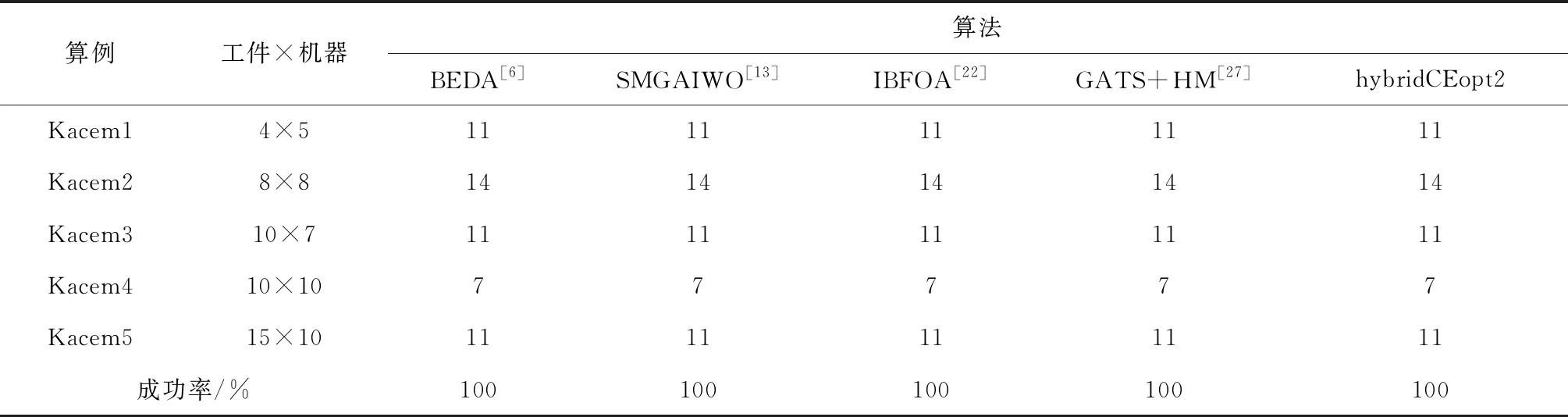



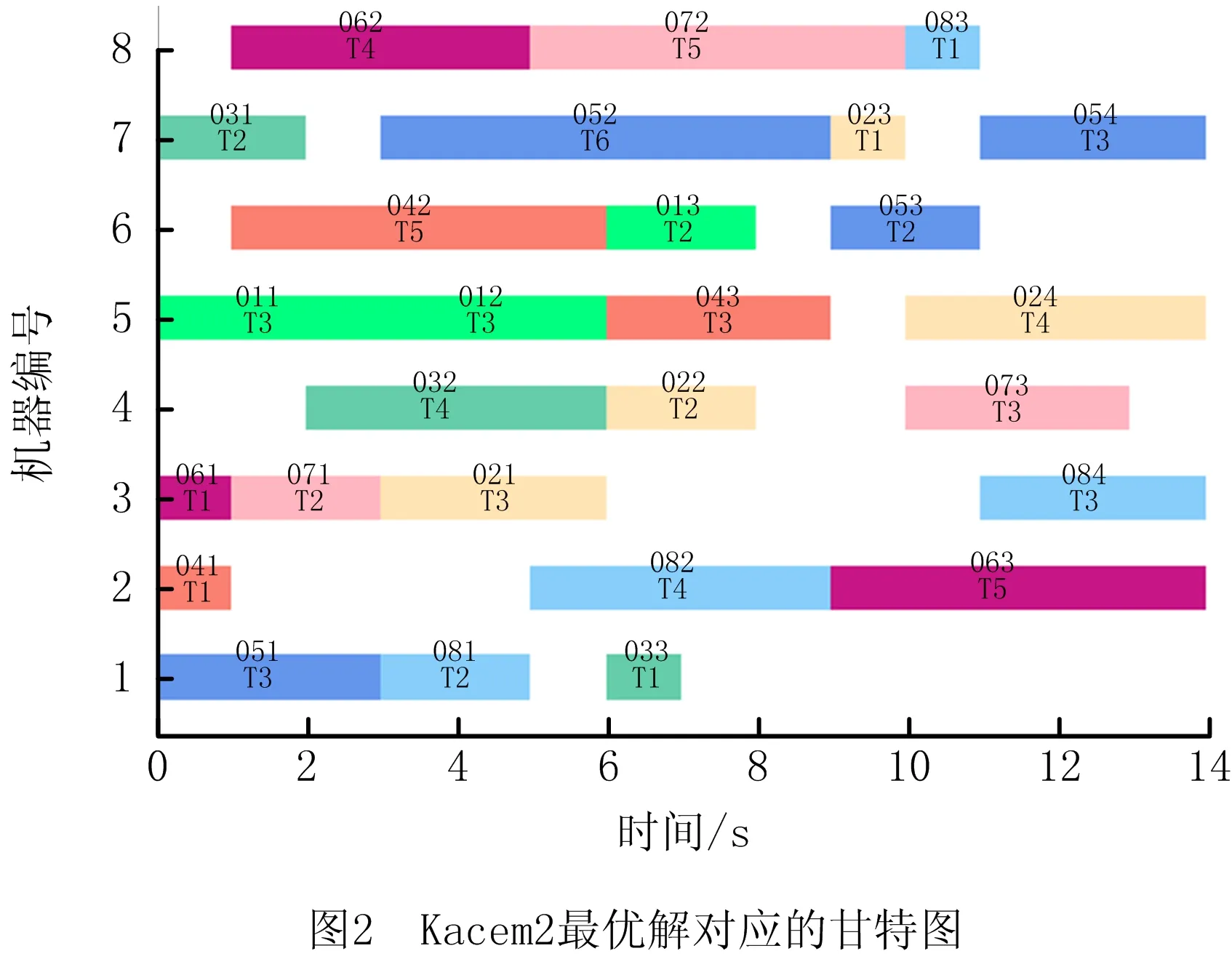
5 结束语
