非线性差分方程的几种特殊求法
2021-06-29王君玉
中学课程辅导·教学研究 2021年35期
◎ 王君玉
非线性差分方程广泛出现在自然科学领域,在物理学、化学、生物学、生态学、工程学中都有着重要的应用,因此如何求非线性差分方程的解是学者普遍关注的问题,对解常见的线性差分方程问题又较成熟的方法,笔者介绍非线性差分方程的几种特殊求法。
一、不动点法
若f(α)=α,则称α为f(x) 的不动点,用不动点法可把非线性差分方程化为等差、等比数列或某些可求解的递推关系,达到求解目的。
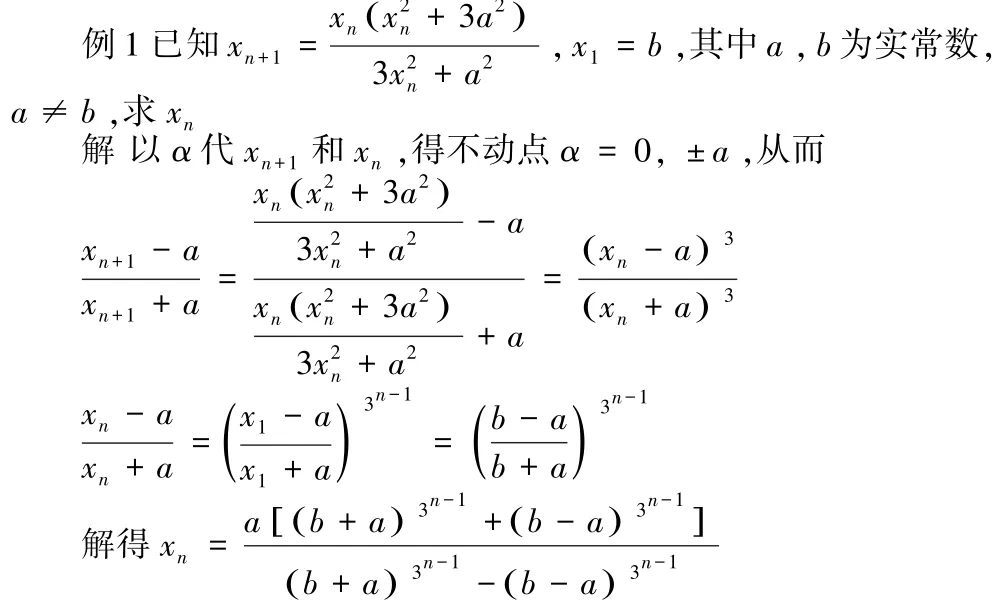
评注:分式差分方程由于它形式的特殊性,在求其通解时它的不动点也必定会有一些更巧的用处,我们可以找出不动点、xn和xn-1之间的等量关系,然后再由递归的方式来计算它的通解。
根据此类方法,笔者编出以下题。

二、取对数法
运用取对数方法,可将含有指数或根式的递推式转化为等差、等比等数列求解。
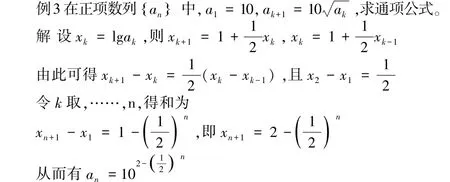
评注:对于指数式或根式的差分方程,两边取对数,可把其化为一阶线性差分方程,求得通解后再转化为题目所求数列的通项。
根据以上方法,笔者编出以下题
例4 解差分方程
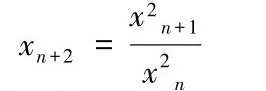
解设zn=lnxn,两边取对数,我们得到
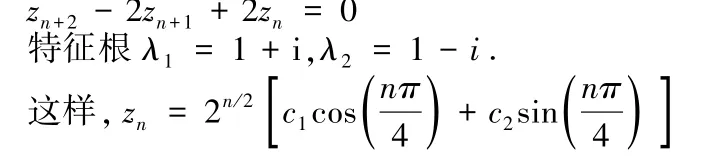

三、代换方法
1.三角代换
运用三角代换,可将差分方程中的分式或根式等化简,使问题便于求解。

评注:根据此类差分方程的特点,暗含某些三角公式的运算形式,应用三角代换后,可去除差分方程中的根式,类比公式即可得出所要求的通项公式。
根据此类方法,笔者编出以下题.

2.分式代换
运用分式代换,可以将复杂的差分方程转化为较简单的差分方程,以便求解。
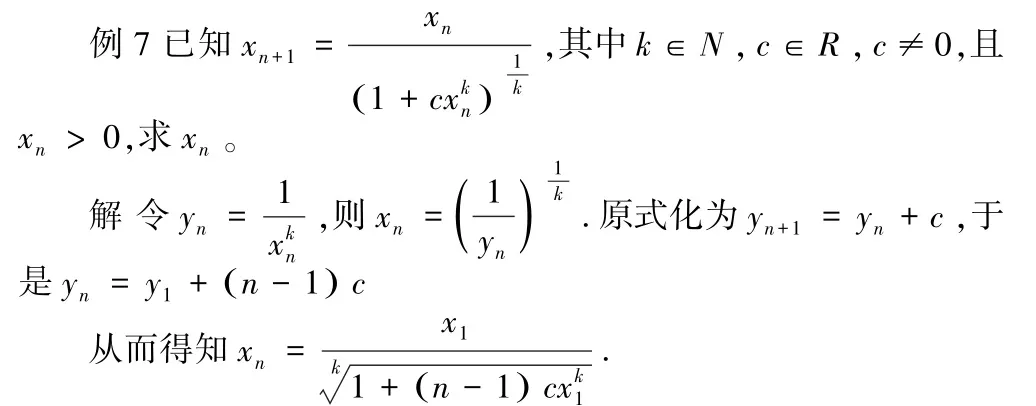
根据此类方法,笔者编出以下题
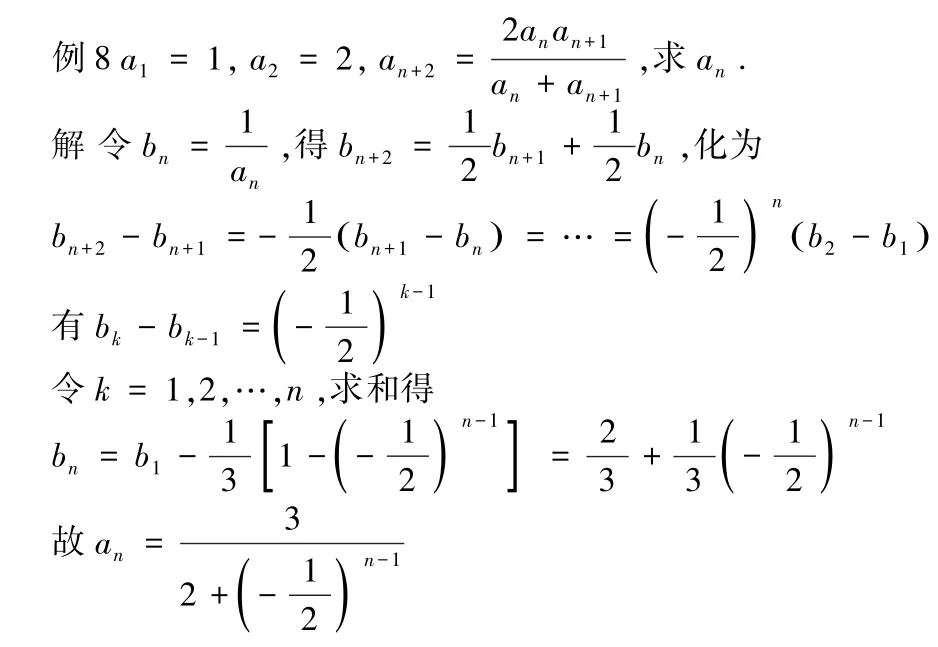
评注:对于较复杂的差分方程形式,可将其用适当的分式代换,变为常见的差分方程形式予以解决。
