特殊高阶函数的构造方法及相关性质证明

孟宜成

(淮南师范学院 金融与数学学院，安徽 淮南 232001)

0 引言

作为数学分析研究的主要对象，函数性质一直是数学研究者所重点关注的问题.特殊函数的性质因其具有一定的特殊性，在理解、接受上具有较大难度[1].因此，对于特殊函数性质能够构造出具有相关性质的函数，对这类函数的理解具有很大帮助.随着级数理论的发展，很多学者借助函数项级数来表示更广泛且具有特殊性质的函数类[2-3].还有学者利用处处连续但处处不可导函数的构造，来提高人们对特殊函数性质的认识[4-5].研究者发现尽管收敛函数项级数中的任意一项均可微或连续，但其所表征的和函数也可能是不可微或不连续的[6].因此，本文以上述主流研究成果为基础，利用正、余弦2种三角函数的自相似性，完成了3种特殊高阶函数的构造，同时对其函数性质进行了验证.

1 处处连续而处处不可微函数

自从魏尔施特拉斯成功构造出处处连续而处处不可导的函数，自相似性概念被逐渐引入到三角函数的相关分析中，以此为基础，对魏尔施特拉斯的函数构造方法进行延伸和扩展，即能实现处处连续而处处不可微函数的构造.

定理1根据魏尔施特拉斯函数构造理论，假定存在1个和函数，即

证明因为|bncosanπx|≤bn同时b∈(0，1)，所以w(x)∈Cb(Rl)(函数在Rl上有界且连续)，其连续性是一致的.

对于下式

按照微分中值定理，存在1个θn使下式成立，即

|cosan(x+h)π-cosanzπ|=

|anπhsinanπ(x+θh)|≤anπ|h|.

继而能够推导出

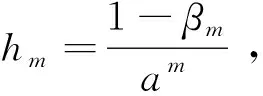
am(x+hm)=amx+amhm=1+am.

在n≥m的情况下，有

anπ(x+hm)=an-mπam(x+hm)=an-mπ(1+am).

由于a为正奇整数，则

cos(anπ(x+hm))=cos(an-mπ(1+am))=

(-1)1- am.

同时

cos(anπx)=cos(an-mπamx)=

(-1)amcos(an-mπβm).

因而可得

由此可推导出

所以下式成立，即

由此即能证明函数w(x)在x处是不可微的.

推而广之，可作以下结论.

定理2假设存在1个函数，即

证明v(x)是明显的处处连续的函数.

对于任意的实数x，由于函数v(x)的差分，有

所以以下关系成立，即

假定1个函数amx=am+βm，其中am为任意1个整数，βm∈[-1/2,1/2]，设

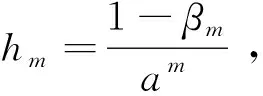
在n≥m的情况下，有

同时

因而可得

|Km|=

所以有

在m→∞同时hm→0的条件下，函数v(x)在x处是不可微的.

若将函数v(x)表示为正弦级数，即

(1)

则也可作出如下结论.

证明对于任意的x∈R，由于函数v(x)的差分，有

Am+Am-1+Am+1.

(2)

设amx=am+βm，其中βm∈[-1/2,1/2]，

(3)

在此条件下，有

(4)

可见式(3)所示的关系依然成立.

所以有

在n≥m的情况下，有

因此下式成立，即

也就是

在m→∞同时hm→0的条件下，函数v(x)是处处是不可微的.

通过实例可以证明必然存在符合定理3的函数v(x).

证明按照特定算法进行计算之后可得

则有

(a+3+π)2-12a-12aπ>0.

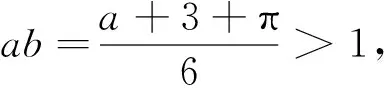
2 处处连续而处处非赫尔德连续函数

定理4的证明过程与定理3相近，其结论成立.

通过以下实例可证明必然存在符合定理4的函数v(x).

例2对于实数b∈[ 1/4，1/2]，假定存在1个正弦函数，即

(5)

v(x)∈Cb(Rl)，但对于任意的正实数s，函数v(x)处处都是非Cs的.

证明对于任意1个x值，v(x)的增量为

按定理3的方式确定hm，那么以下各关系式成立，即

|Tm≥bm|，

因此，对于任意的b∈[ 1/4，1/2]，有

所以对于1个任意的正数s>0，函数v(x)处处都是非Cs的.

3 处处赫尔德连续而不更高阶连续函数

例3假定a为正数，b∈(0，1)，对于1个任意的正数s>0，存在函数U(x)，其表达式为

(6)

该函数处处Ca赫尔德连续但不更高阶Ca+s连续.

证明正弦函数sinx的Ca模特征为

所以有

由此可说明U(x)∈Cb(Rl).

根据例2中的证明方法，以下关系式成立，即

因此可得

进而能够证明，对于1个任意的正数s>0，函数U(x)处处赫尔德连续但不更高阶连续.

4 自相似性方法的应用

正、余弦函数共同具备的周期性特征形成了这2种三角函数的自相似性.即按照以下方式便能对函数中的相关项进行预估或计算，从而证明相应的结论.

1) 对于余弦函数的傅里叶项级数，在m≤n的条件下，设定an/am为正奇数，则

由上式可见，计算结果与n无关，因此在m≤n的条件下，

|cosπan(x+hm)-cosπanx|=1+

此外，

|sinπam(x+hm)-sinπamx|=1+sin|βm|π≥1.

由此可直接估算|Am|且在m≤n的条件下，通过下式

可直接估算出余项|Am+1|.

3) 对于任意形式的三角函数，其中的bm↓0且趋近速度极快，同时由于ambm↑+∞，因而am↑+∞的趋近速度也是极快的.在对am和bm的具体数值进行选择时，需要同时控制余项|Am-1|和|Am+1|，以此来简化计算或估计的过程.

对于通过函数周期性所形成的自相似性，现有的研究成果中包含了一定数量的实例.

依据本文所提出的方法可对例4和例5进行证明，只要对hm进行适当的取值，使下式成立，即

5 结语

魏尔施特拉斯对处处不可导函数的构造方法打开了特殊高阶函数的构造思路，本文依次构造了处处连续而处处不可微函数、处处连续而处处非赫尔德连续函数、处处赫尔德连续而不更高阶连续函数，证明了对于收敛的函数项级数，即使所有项均为连续或可微的，由其构成的和函数也不一定是连续或可微的.同时通过实例验证了函数的自相似性.对于特殊高阶函数的相关研究，本文所提出的构造方法具有很高的参考价值.在本次研究过程中，多次运用了傅里叶级数的局部处理方法，在今后的研究中将更注重探索解决整体问题的方法.