基于膜结构假定的无背索斜拉桥主梁轴力解析
2021-06-29黄晨光林丽霞丁南宏
黄晨光,林丽霞,丁南宏
(兰州交通大学 土木工程学院,甘肃 兰州 730070)
0 引言
随着无背索斜拉桥跨径的不断增大,拉索的长度逐渐增加,倾角逐渐减小,使得拉索的垂度效应影响逐渐显著,从而令拉索的支撑效率由近塔处向远端逐渐降低.人们通常采用增大索力的方法来改善远端拉索效率低下问题,但会使主梁轴力整体变大,加重近塔处主梁截面负担.同时,索力的非均匀增大、无背索斜拉桥的特殊构型及拉索的垂度效应,均会使主梁轴力变化出现非线性特征,此时简化过于严重的线性轴力分析将不再适用,轴力的计算也趋于复杂.因此,如何基于轴力的非线性变化进行分析,快速计算出主梁轴力便成为了一个重要问题.
在探究斜拉桥结构体系的过程中,人们发现主梁轴力是限制斜拉桥跨径增大的主要因素,并探究出许多计算轴力的方法[1-3].丹麦学者Gimsing将扇形体系转化成辐射式布置,然后按照辐射式布置求得主梁轴力分布函数[4].王伯惠基于平均索法的思想,将一侧若干根拉索等效为1根虚拟索,以此来计算近塔处主梁轴力[5-6].吴万忠等在不考虑无索区的前提下,将索膜当作连续体分析,推导了有索区主梁轴力近似公式[7].彭旺虎等认为无背索斜拉桥拉索倾角的变化范围较小,故在计算主梁轴力时,取拉索倾角的平均值,按等角度计算,给出了理想成桥状态下的主梁轴力递减函数[8].文献[4]和[8]所做简化实际上改变了该桥原有布索方式.文献[7]未考虑无索区对轴力函数的影响,适用于大跨度斜拉桥有索区梁长远大于无索区梁长的情况.无背索斜拉桥以中小型跨径居多,且主塔呈倾斜状态,故需要考虑无索区及斜塔倾角的影响.
针对无背索斜拉桥主梁轴力解析问题,本文基于平衡荷载理论及膜结构假定,分别推导索面按照辐射式、扇形式及竖琴式布置时,无背索斜拉桥有索区梁段主梁轴力沿梁长变化的连续函数,利用Heaviside函数进行修正[9],得到含无索区及斜塔倾角影响的主梁轴力解析式.
1 主梁轴力解析式
在无背索斜拉桥结构中,主梁轴力曲线是1条以主梁拉索锚固为分界点的阶梯型分段函数曲线,随着拉索数量增加,单位梁长内的拉索密度增大,轴力曲线每两阶梯间的级差逐渐减小,曲线形式逐渐由离散状向平滑过渡.因此,在密索体系斜拉桥中,可以将拉索体系近似看作一个平面索膜,当作连续体分析,且由于塔的位移较小,因此不考虑斜塔的抗推刚度.
1.1 扇形式索面布置
假设梁体的恒载荷载集度为q0,主梁两侧无附加轴力,拉索为等索距布置,且主梁与主塔上锚固区的索距比为k,塔高为h,主梁索面两侧无索区梁端长度为L0、L1,有索区梁端长度为Ly,斜塔倾角为θ,最外侧2根拉索在主梁上锚固点位置的横坐标为x1、x2.将拉索索面看作一膜结构,当作连续体分析,作用在梁段Ly.主梁轴力计算简图如图1所示.

(a) 斜拉桥结构
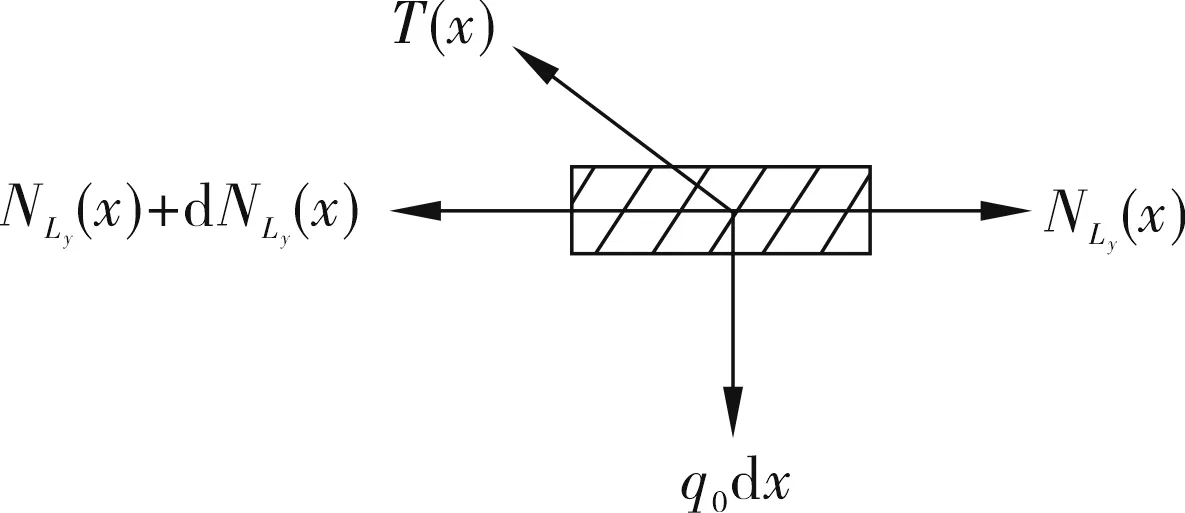
(b) 主梁微段受力图1 主梁轴力计算简图
在有索区梁段Ly内取一微段,则索膜纤维在斜塔及主梁上的位置关系在笛卡尔坐标系下可用函数表示为
(1)
主梁有索区微段的平衡条件为
(2)
联立式(1)~(2)得
(3)
将式(3)积分,令a=1/tanθ、b=h-ce、c=ksinθ、e=L0+Ly,则有索区主梁轴力表达式为
NLy(x)=
(4)
由式(4)中的对数函数项可以看出,轴力沿梁长方向有着明显的非线性分布特征.
1.2 竖琴式索面布置
竖琴式布置时,各拉索间相互平行,基于几何相似原理,有
(5)
式中:λt、λc分别为斜塔及主梁上的拉索间距.
将式(5)带入式(4),可得竖琴式索面布置下的主梁轴力解析式为

(6)
1.3 辐射式索面布置
当无背索斜拉桥索面布置为辐射式时,拉索在塔上集中锚固于一点,塔上锚固区索距为0,故索距比k值恒为0,这使得式(4)中的对数项出现“∞·0”的形式,使得方程无定解.将(4)式整理为
(7)
将式(7)中的对数项进行泰勒级数展开,有
(8)
取级数的前2项带入式(7),整理得
(9)
式(9)即为辐射式索面布置下,无背索斜拉桥有索区主梁轴力解析式.
2 主梁轴力解析式修正
通过上述推导,得到了考虑斜塔倾角时,扇形式、竖琴式、辐射式索面布置下的主梁有索区轴力解析式.为进一步考虑无索区梁段对主梁轴力的影响,利用Heaviside函数性质对主梁轴力解析式进行修正.
假设无索区梁段所受恒载由索面边缘的1根拉索及支座共同承担,可看作相应横截面上作用1个轴力,则两侧无索区产生的轴力为
NL0=η0q0L0tanα,
(10)
NL1=η1q0L1tanβ,
(11)
式中:η0、η1分别为近塔处与远端无索区主梁恒载修正系数,与恒载等效为集中力后的作用点有关[10].
引入Heaviside函数H(x),为保证有索区梁段轴力函数值域的完整,定义H(x)为

(12)
式(7)中x不取坐标原点,认为最大轴力存在于近塔处.则无背索斜拉桥主梁轴力分布表示为
N(x)=(NL0+NLy(L0)+NL1)H(x)+
(NLy(x)-NLy(L0)-NL0)H(x-x1)-
(NLy(x)+NL1)H(x-x2).
(13)
若不考虑主梁无索区及斜塔倾角影响,则式(13)退化为
N(x)=
(14)
可知式(14)与文献[7]中所推导的轴力计算公式一致.
3 算例分析
将无背索斜拉桥的拉索分别按照辐射式、扇形式和竖琴式布置,主梁采用钢筋混凝土梁.根据第1节理论及公式,可得到主梁截面轴力沿梁长变化曲线,如图2所示.

图2 主梁轴力曲线
由于竖琴式布索时,各个拉索与主梁间的夹角相同,使得拉索在水平方向上的投影值近乎相等;
而竖琴式及辐射式布索时,随着拉索逐渐向近塔处靠近,拉索角度逐渐增大,其水平投影值逐渐减小,且减小的速率存在非线性特征.因此,竖琴式索面布置时,近塔处主梁轴力最大,扇形式次之,辐射式最小.辐射式索面布置时,主梁轴力沿梁长方向的非线性变化最为显著.
为验证主梁轴力解析式的准确性,以扇形式索面布置的无背索斜拉桥为例,分别采用索膜方法、文献[4]方法及有限元法计算主梁轴力.恒载集度取281.3 kN/m.η1、η2分别取0.20、0.13.选取主跨的近塔处、1/8截面、1/4截面、3/8截面、1/2截面为关键位置截面.主要结构参数如表1所示,根据表1中结构参数建立有限元模型,如图3所示.

表1 主要结构参数
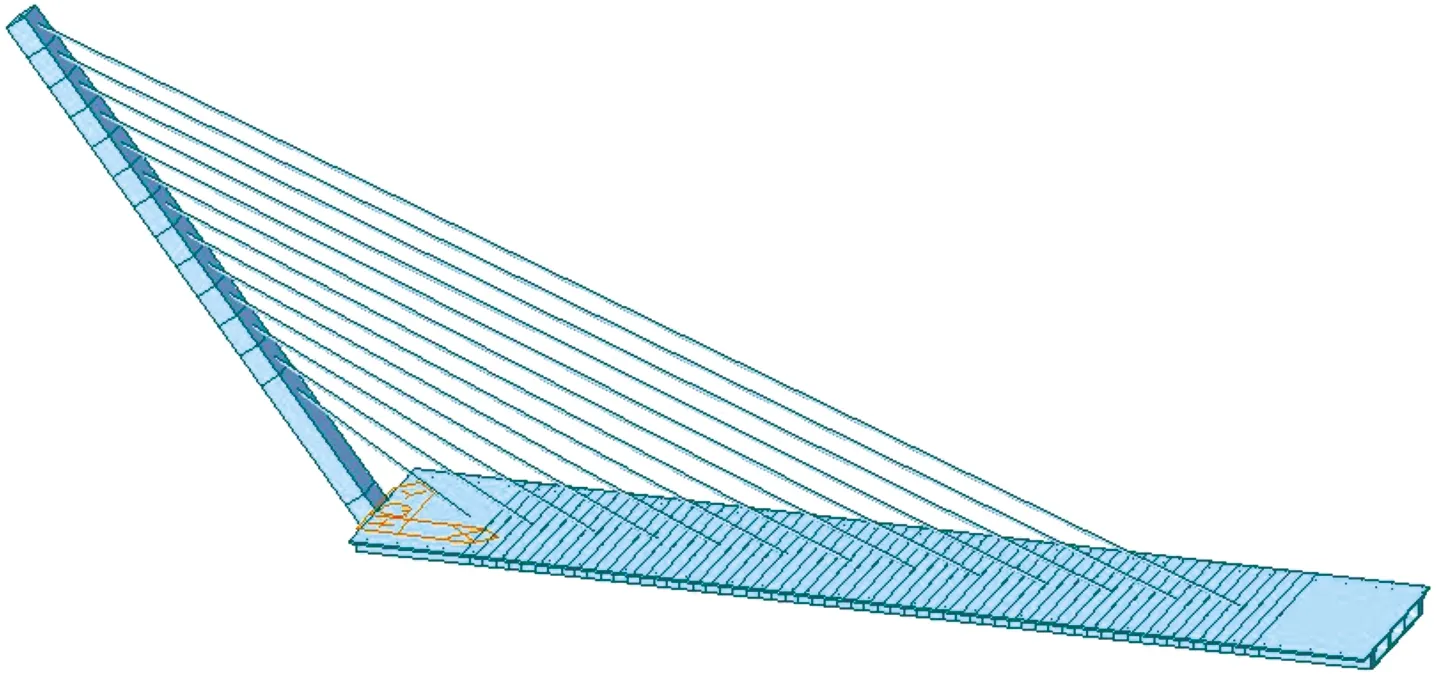
图3 无背索斜拉桥有限元模型
有限元模型共采用82个节点,89个单元,主梁与斜塔均采用梁单元,主梁为简支结构,斜塔底部固结,拉索采用桁架单元,与梁塔直接通过节点连接.由于不考虑斜塔的抗推刚度,因此采用强塔弱梁结构.计算结果及误差如表2和图4所示.

表2 主梁轴力计算结果及误差

图4 扇形式布索主梁轴力曲线
由表2及图4可见:文献方法计算主梁轴力结果偏小,与有限元法结果相差较大;本文方法与有限元法计算结果吻合良好,偏差较小且分布较为均匀.
此外,仍取表1的主要结构参数为基础,在上述模型的基础上,令主梁锚固点位置不变,改变斜塔上锚固点位置,按竖琴式布置索面.联立式(6)、式(9)~(10)、式(13),用本文的方法计算主梁轴力.计算结果与有限元法结果对比如图5所示.
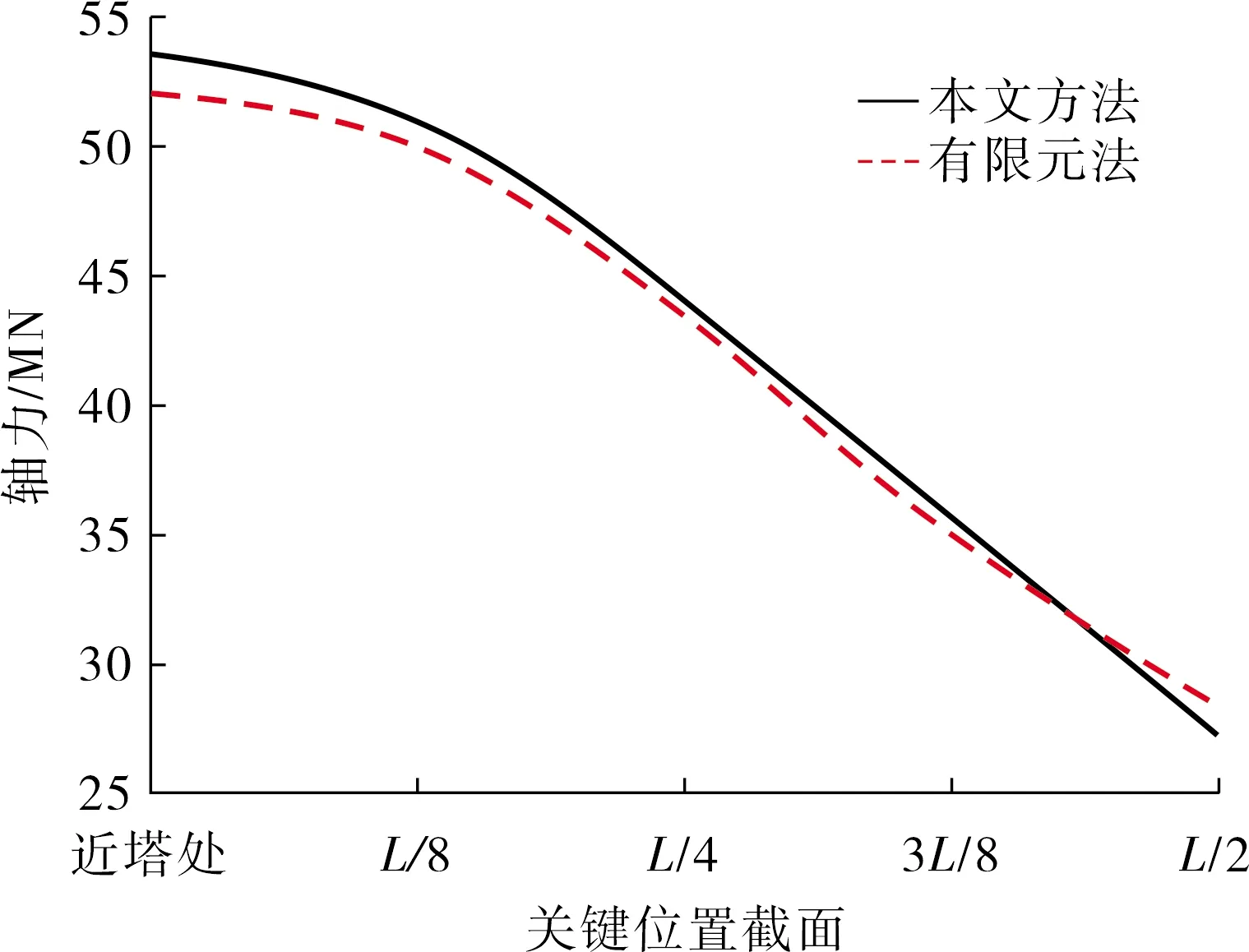
图5 竖琴式布索主梁轴力曲线
仍以上述模型为基础,保持主梁锚固点位置不变,塔上锚固点均取塔顶位置,按辐射式布置索面.联立式(9)~(11)及式(13),按本文方法计算主梁轴力,并与有限元法结果对比,如图6所示.
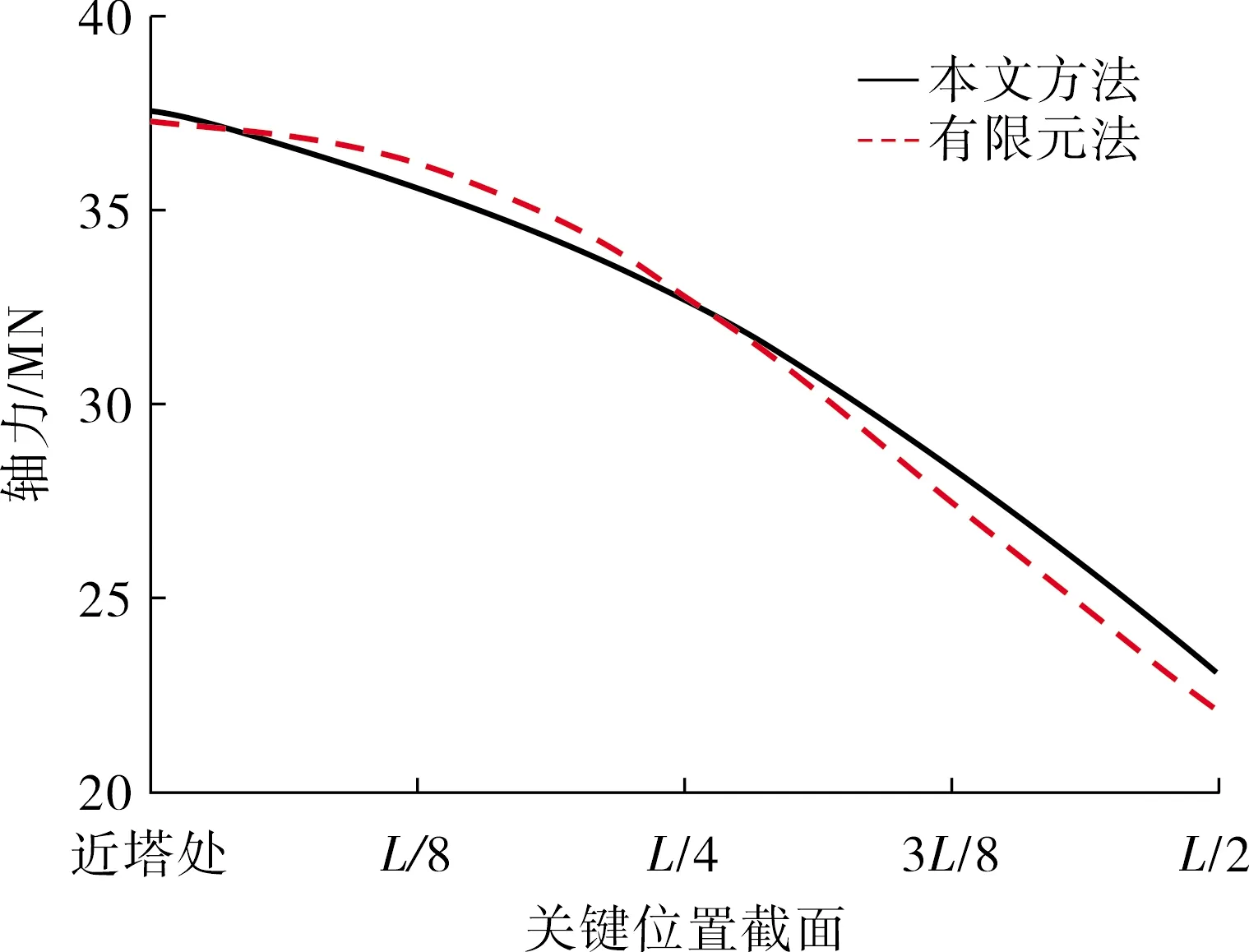
图6 辐射式布索主梁轴力曲线
由上述算例验证结果可以看出:在不同索面布置下,若无索区长度在跨径中不占较大比重,有索区内侧端点的轴力值与近塔处的轴力值可能较为接近;但前者始终小于后者,无索区梁长比重越大,该部分差异越明显.这是由于无索区同样受到荷载作用,该部分荷载由拉索和支座共同承担,因此拉索索力增大,索力的水平投影增大,使得轴力增大.在不用有限元法计算的情况下,文献方法所求结果相比实际结果较小,无法确定其安全系数,不利于设计.而由图4~6可以看出,本文方法与有限元法计算结果较为接近,误差均在5%左右,且整体结果略微偏大,无须确定安全系数,是更偏于安全的计算方法.
4 结论
1) 本文针对无背索斜拉桥结构,基于平衡荷载理论及索膜假定,考虑斜塔倾角及无索区影响,推导了多种索面布置下的主梁轴力解析式.通过算例分析,其计算结果与有限元法结果较为吻合,误差均在5%左右,对实际结果有所包络,是更偏于安全的计算方法.
2) 由本文所推导的主梁轴力解析式可知,主梁轴力与荷载、跨径、斜塔高度及索距比有关,适当增加斜塔高度,减小荷载或跨径,都可以降低主梁轴力,减小近塔处主梁截面的负担.
3) 竖琴式布索的无背索斜拉桥主梁轴力整体较大,扇形式次之,辐射式最小;但辐射式布索时轴力变化的非线性特征最明显,因此在设计时根据布索形式的不同,需要对主梁不同位置截面的材料及构造有所侧重.
