核心素养下小学数学数形结合思想的渗透与应用

福建省三明市尤溪县西城中心小学 林玉琼

随着教育改革进程的发展，核心素养理念逐渐深入人心。尤其是在小学数学教学中，在核心素养理念的支持下培养学生数形结合思想成为顺应现代教育主题的一种表现，而对其进行研究，是为了更好地将数学结合思想融入小学数学教学中，以此提高数学教学质量。以下将对核心素养理念下渗透和应用数形结合思想的重要性和有效策略进行研究。

一、在小学数学教学中渗透和应用数形结合思想的重要性

处于小学阶段的学生，他们的认知能力和思维能力还没有得到明显的发展，所以在他们面对抽象的数学知识和概念时，非常容易产生困惑和不解，这对于他们理解问题和解决问题会造成较大的阻碍。而将数形结合思想融入小学数学教学中能够明显改善这种状况，让学生在图形与数字的转化中将抽象的数学概念转化为更加直观和清晰的图像和文字，使他们深入理解数学概念，并能将其应用到解决实际问题中，降低小学生学习数学的难度，让他们更积极地投入数学学习过程中。这不仅能够提高小学数学教学的效率，还能促进学生直观思维能力以及数学推理能力的形成，让他们长久地保持对数学知识的兴趣。

二、核心素养下小学数学教学渗透和应用数形结合思想的策略

（一）运用“以形助数”的方法，增强小学生的直观想象能力

“以形助数”是数形结合思想中的重要组成部分，将其渗透在小学数学教学中能够使学生通过图形的直观性促进他们对“数”的概念的理解。这样的方式能够增强数学学科核心素养中的直观想象能力，促使学生将抽象的概念转化为形象的图形。

1.利用基本图形认识数的概念

由于思维能力和认知能力的限制，小学生一时之间很难理解和运用“数”的概念，也无法准确地认识到概念的具体指向和范围，这时“以形助数”的理念就能够发挥巨大的作用。教师可以在数学教学中利用学生常见的几何图形，引导他们掌握图形与数字之间的关系，让他们能够轻松地将繁杂的数学概念转化为直观化的图形，这不仅能够降低他们在学习中的难度，也有利于进一步增强他们的直观想象能力，促进他们数学思维的形成和发展。

例如，在人教版小学数学六年级上册“百分数”的教学中，学生初次接触“百分数”的概念难免会产生困惑，这时教师就可以发挥“以形助数”的作用。在讲解“百分数”的概念和引导学生应用概念解决问题的时候，可以事先让学生利用直尺画出一个长为100毫米，即10厘米，宽为1厘米的长方形，然后找出几个百分数的实际例子，如“百分之十四”“百分之五十”等，让学生在长为100毫米的长方形中用特殊标号笔画出长为14毫米的长方形，接下来引导学生观察大长方形与小长方形之间的关系，促使学生在观察图形的过程中明确“百分数”的概念。为了加深学生对概念的理解，增强他们的直观想象能力，教师也可以引导学生根据给出的百分数，自主画出其他图形，通过这样的方式不仅可以使学生掌握数学概念，还能让他们将数学概念与实际生活联系起来。在核心素养理念的指导下，学生的直观想象能力也会进一步增强。

2.利用线段实物化解抽象问题

直观想象能力是核心素养中的重要组成部分，而将抽象的数学问题转化为形象化的图形，是培养和增强学生直观想象能力的一种有效途径和方法。除了基本的几何图形之外，线段和实物也是化抽象数学问题为直观图形的一种手段。因此，为了进一步加强学生的直观想象能力，提升他们分析数学问题和解决数学问题的能力，教师可以利用线段图和生活中的实物进行教学，充分体现出“以形助数”的数形结合理念。

首先，利用线段图帮助学生更加深入地理解数学问题，让学生将复杂的数学问题转换为简单的线段，在线段的组合中明确问题所蕴含的概念和知识，并探索出解决问题的方法和技巧。例如，在五年级上册“数学广角”中的“植树问题”教学中，教师在引导学生解决问题的过程中，可以要求学生将题干中的条件转换为线段，比如：“同学们在长度为100米的道路旁植树，每5米要栽一棵树（两端也要各栽一棵树），那么同学们一共需要栽多少棵树？”学生面对这一应用问题时，在短时间内很难找到解决办法，所以教师可以让他们画出100毫米的线段，根据题目中的条件在线段两端各画出一个点，再以间隔5毫米的规律，在线段中做出标记，从而完成解题的初步步骤，激发他们的数学思维，让学生在直观化的线段中探索解决数学问题的方法，化解抽象问题带来的困难，以此增强他们的数学直观想象力。其次，利用实物将抽象的数学问题转化为直观的思维。例如，在“简易方程”的教学中，为了化解抽象数学问题带来的困难，让学生利用直观想象力解决数学问题，教师可以准备一个天平，两个完全相同的长方形储物盒，还有9个完全相同的小球，将两个盒子放在天平的两端，分别放入三个小球，这时学生会发现天平保持平衡。然后在其中一个盒子中放入一个球，引导学生说出此时天平的状态，再在另一端放入一个小球，反复进行实验之后，学生会发现，在天平两端加减同样数量的小球时天平会保持平衡，从而让他们明白“简易方程中，方程两端加减同样的数字，等式的两端仍然保持相等”。

（二）运用“以数解形”的方法，提升小学生的运算分析能力

1.利用图形的数字特征，引导学生掌握图形的结构

除了利用直观化的图形缓解数学概念的抽象性之外，融合数形结合思想也可以从数学公式定理出发，让学生更加准确地掌握图形的结构以及不同图形之间的关系，让他们对不同的图形构建起清晰的数量关系，从而避免因缺乏实物道具而产生的理解偏差。因此，教师在小学数学的实际教学过程中，为了帮助学生更好地理解图形的结构和关系，应该积极主动地在图形和数学公式定理间建立起联系，并引导学生在学习新知识的过程中应用数形之间的关系，通过运算、分析掌握图形知识。

首先，在认识图形的结构方面，以“长方体和正方体”教学为例，教师可以利用数字的特征，让小学生记住长方体和正方体的性质，比如长方体是一个底面为长方形的直四棱柱，它有6个面，有8个顶点，还有12条棱，所以教师可以引导学生记忆“6+8+12”的数字组合。通过数字的组合让学生理解长方体的性质，这样不仅可以使学生了解图形的结构，还能有效锻炼学生的运算分析能力。其次，在认识不同图形之间的关系方面，可以将人教版小学数学中的“梯形”“平行四边形”和“三角形”结合在一起，第一步将梯形的上底设为b，下底设为a，高设为h，将所有图形的面积都设为s，所以表示梯形面积的公式就为s=（b+a）×h÷2，而当b与a相等时，即s=（a+a）×h÷2，梯形就转化为了平行四边形，又如b等于0时，即s=（0+a）×h÷2，这时梯形又转化为了三角形。通过三个略有不同的面积公式，使学生明白三个图形之间的关系，即当梯形的上底和下底相等时，梯形就转化为了平行四边形，而当梯形的上底为0时，梯形就转化为了三角形。通过这样的方式，能够让学生在公式的运算和转换中，理解图形之间的关系，从而实现数形结合思想的价值和作用。

2.利用数学列式计算，引导学生体会图形的规模

虽然图形以其形象化的特点为人所知，但是只有实现数字与图形的完美统一，才能真正突破数学的抽象性，使小学生更加深入透彻地理解数学概念、解决数学问题。因此，为了引导学生进一步体会图形的规模，教师可以利用数学的列式计算，让学生在运算和分析的过程中把握图形的实际规模，形成准确的认知。例如，在“多边形的面积”教学中，教师可以引导学生将生活元素引入数学学习中，利用校园内的平行四边形花坛，更加深入地体会图形与数字之间的关系，列式计算出花坛的实际面积，让他们将实际的图形与真实的面积结合在一起，通过数学运算和分析对生活中的图形有一定的了解。首先，教师应该为学生准备软尺，让学生分组合作量出平行四边形花坛的边以及高，最终量出平行四边形花坛的底边为6米，高为3米（见下图），然后进一步利用平行四边形的面积公式计算出花坛的面积，即面积=底边×高，也就是“花坛面积=6×3=18（平方米）”，以此引导学生体会图形的规模，让他们树立生活化数学思维。通过这样的方式，不仅可以进一步巩固学生的运算知识，还能让他们对图形具有更加简洁准确的认识

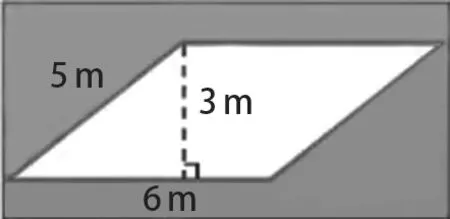
平行四边形花坛示意图

总而言之，在小学数学教学中，围绕核心素养渗透数形结合理念是非常具有现实意义的，它能够解决抽象数学概念给学生带来的学习阻碍，能够让学生更加深入地理解数学知识，并不断增强他们运用数学思维解决问题的能力。在核心素养的指导下进行教学，能够使学生具备数学感悟、直观想象、运算分析等能力，也能促进学生综合素质的形成和发展。