沉井接高过程中砂桩复合地基固结承载特性

陈培帅，潘亚洲，梁发云，李德杰

(1. 中交第二航务工程局有限公司 长大桥梁建设施工技术交通行业重点实验室, 武汉 430040; 2. 同济大学 地下建筑与工程系, 上海 200092)

我国深水大跨桥梁建设如火如荼，沉井基础因其具有刚度大、承载力高和整体性能好等优点而得到广泛应用.由于大型沉井自重大，未经过处理的软弱地基往往难以满足承载力要求，需要采用砂垫层结合砂桩处理等方式进行地基加固[1].目前，砂桩的成桩直径可达1.6～2.0 m，施工最大深度近60 m，最大置换率可达70%[2].

沉井基础逐节接高施工的时间间隔往往较长，例如，马鞍山长江大桥南锚碇沉井首次下沉结束后经过40天左右的接高施工后才开始第二次下沉[3].在此期间，地基土在沉井自重荷载作用下已发生一定程度固结，其有效应力提高，导致土体强度增加，增大了砂桩的侧向约束力，从而使砂桩的承载力也相应提高[4].闫澍旺等[5]提出了考虑固结引起土体强度增长的天然地基承载力计算方法，通过分析两个堆山工程案例发现地基固结度达到60%时的承载力比其天然强度提高了80%左右.Munfakah等[6-7]研究发现，复合地基固结速率远大于天然地基.因此，沉井接高过程中自重应力引起的地基土固结会使砂桩复合地基承载力产生明显增长.在沉井下沉施工过程中，如果忽视固结引起的复合地基承载力增长，有可能因地基承载力过大导致沉井难以下沉[8].

国内外学者对砂桩复合地基的固结特性和承载性能均进行了大量研究[9-13].地基固结包括竖向固结和水平向固结，根据规范[14]，砂桩复合地基水平向固结度受砂桩内部径向渗流的影响较大.目前，考虑砂桩内部径向渗流的复合地基固结解大多基于外部荷载瞬时施加且地基中的附加应力在桩体深度范围内均匀分布的假定.实际上，沉井接高施工为现场分节浇筑，耗时较长，故可认为沉井接高加荷为线性加载.此外，沉井主要由四面垂直井壁和众多隔墙组成，首次接高时沉井自重荷载通过刃脚和隔墙下的混凝土垫层和砂垫层传递给砂桩复合地基，荷载形式为条形荷载.李建国等[15]研究了条形荷载下复合地基附加应力分布形式的数值模拟解和Boussinesq解，结果表明附加应力均沿深度逐步衰减，接近线性分布.

砂桩复合地基承载力的理论计算方法主要有两种，即桩土面积比法和桩土应力比法[16].桩侧土体所能提供的最大侧限力是桩土面积比法计算的关键，常用计算方法有Brauns计算法、Wong方法、Hughes-Withers方法、被动土压力法及圆筒形孔扩展理论计算法等[17].朱小军等[18]采用上述方法计算了挤密砂桩及复合地基的极限承载力，并与模型试验地基承载力值进行对比分析，发现Wong方法和被动土压力法与模型试验结果较为接近，误差在5%左右.然而，目前针对沉井接高过程中考虑固结对复合地基承载能力影响的研究较少，我国规范中同样很少考虑固结引起的地基承载力增量.例如，沉井规范[19-20]仅给出了各种地基土的承载力建议值，复合地基规范[21]给出了基于桩土应力比法的地基承载力公式，均未考虑固结的影响.

本文以某大桥南锚碇沉井基础的砂桩复合地基工程为背景，探讨了沉井接高过程中砂桩复合地基的固结特性，分析了加荷历时和砂桩置换率等因素的影响规律，然后分别基于桩土面积比法和规范建议的桩土应力比法推导了考虑固结影响的砂桩复合地基极限承载力表达式，并与地基实测的天然承载力对比.该方法考虑了沉井下沉施工前地基土固结产生的影响，避免了因低估地基的实际承载力而导致沉井滞沉问题，可为沉井接高过程中考虑固结影响的复合地基承载力计算和确定合理的沉井下沉施工方案提供参考.

1 工程概况

1.1 工程背景

某大桥南锚碇大型陆上沉井采用钢壳与钢筋混凝土相结合的型式，平面尺寸为70 m×63 m，总高度为67.5 m.标准壁厚2.0 m，隔墙厚1.2 m，共设置30个矩形井孔，平面尺寸为10.0 m×10.84 m，如图1所示.沉井沿高度方向共分为13节.第1节为钢壳混凝土沉井，高8.0 m，刃脚高1.9 m；第2至第13节为钢筋混凝土沉井，其中第2节高6.0 m，第3节高4.0 m；第4节至第11节高均为5.0 m，第12节高3.5 m；第13节高6.0 m.

沉井分4次接高、3次下沉，第1次接高前4节，采用排水辅助下沉15.5 m；第2次接高3节，采用不排水开挖下沉12.0 m；第3次接高5节，采用不排水开挖下沉38.5 m；第4次接高第13节.

1.2 地质条件

南锚区上部土层为海积淤泥质黏土、海积淤泥及流塑土，厚度为35.5～40.0 m(表层有少量粉细砂分布)，具有高压缩性、易扰动变形、承载力低等特点，工程性质差，主要地层参数见表1.表中：h为层厚；c为黏聚力；φ为摩擦角；ρ为天然密度；P为极限承载力.淤泥质黏土层为第1层土，层厚9.3 m，砂桩加固后通过载荷试验测得地基的天然承载力为402.2 kPa.针对沉井首次接高过程讨论地基承载力时，沉井尚未开始下沉，故在此选取第1层砂桩加固土层作为研究对象.

表1 部分土层物理力学性质指标Tab.1 Physical and mechanical property indicators of partial soil layers

为防止早期施工过程中产生突沉、偏沉、反涌和超沉等工程问题，该工程对淤泥地层采用砂垫层+砂桩进行加固处理.砂垫层厚3 m，砂桩加固土层厚度为33 m.砂桩直径60 cm，置换率36%，平面如图2所示.

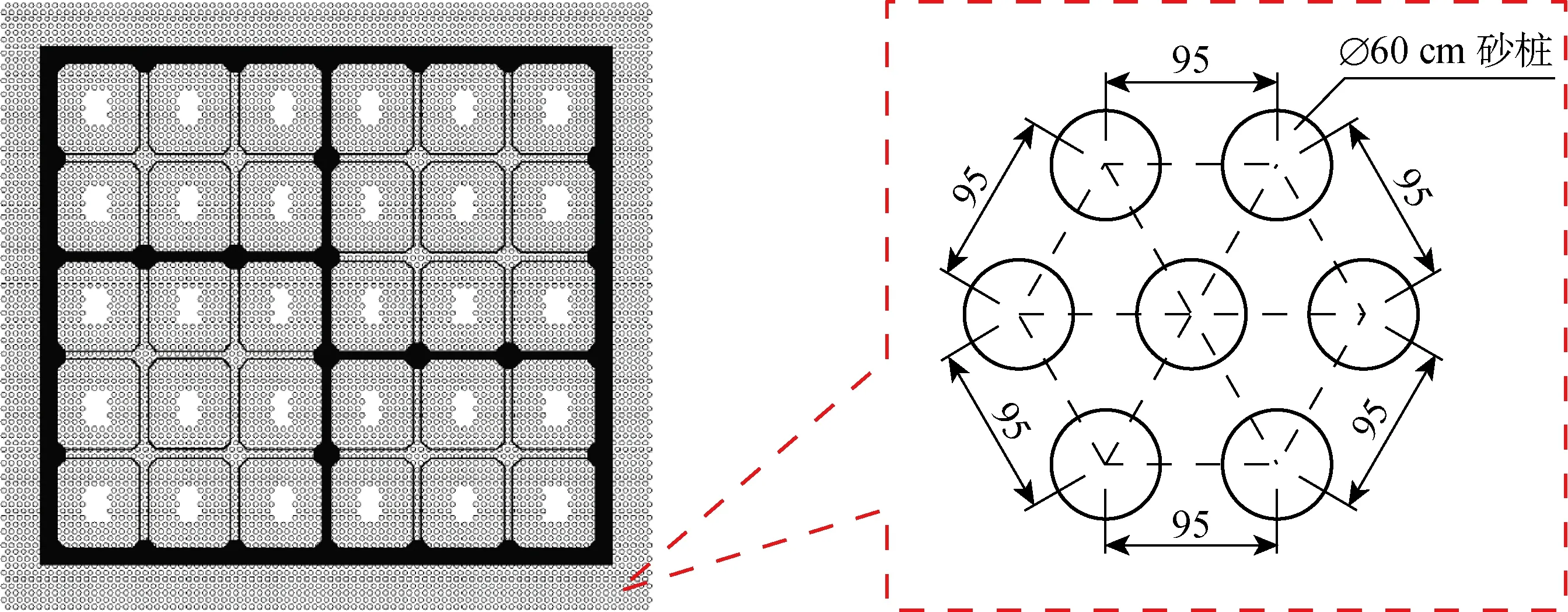
图2 砂桩平面示意图(cm)Fig.2 Plane sketch of sand pile (cm)

2 砂桩复合地基固结特性

2.1 砂桩复合地基固结度解析表达式

卢萌盟[22]基于等应变条件，在不考虑砂桩内部径向渗流的条件下，给出了附加应力沿深度线性变化且荷载线性加载时砂桩复合地基的总固结度解析解，可用于计算沉井分节接高时的复合地基固结度，具体表达式为

(1)

式中：U为单层复合地基固结度；t为时间，tc为加荷历时；PB、PT分别为软土层底面、顶面的平均附加应力；M=0.5π(2k-1)，k=1,2,…；

βm=

ch为土体的水平向固结系数，kv为土体的竖向渗透系数，kh为土体的水平渗透系数，kc为桩体的竖向渗透系数，H为土层的厚度，re为影响区半径，rc为桩体半径，n=re/rc，Y=Ec/Es，Ec为桩体的压缩模量，Es为土体的压缩模量，

2.2 沉井基础下砂桩复合地基固结特性分析

2.2.1加载历时对砂桩复合地基固结度的影响 南锚碇沉井首次接高施工时，前4节沉井在砂垫层上依次接高，每节沉井正常接高施工需要26天左右，接高完成后整体下沉.沉井接高时的自重应力为施加于地基上的荷载，即基底压力.基于Boussinesq应力解，通过MATLAB编程分析沉井基础下砂桩复合地基的附加应力分布，分别得到4节沉井接高完成时砂桩复合地基的顶部附加应力与第1层土的底部附加应力.表2列出了4种工况，第x种工况为仅接高前x节沉井(x=1,2,3,4)，接高结束后停止施工.

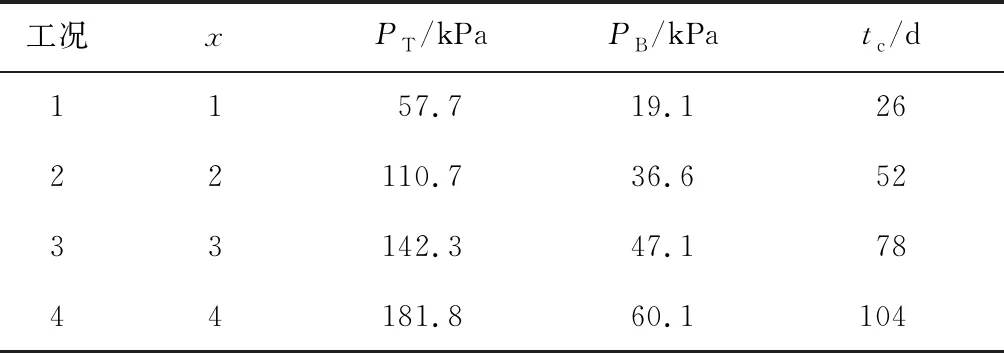
表2 4种工况Tab.2 Four working conditions

根据式(1)计算4种工况下不考虑桩体内径向渗流的砂桩复合地基固结度，结果如图3所示.

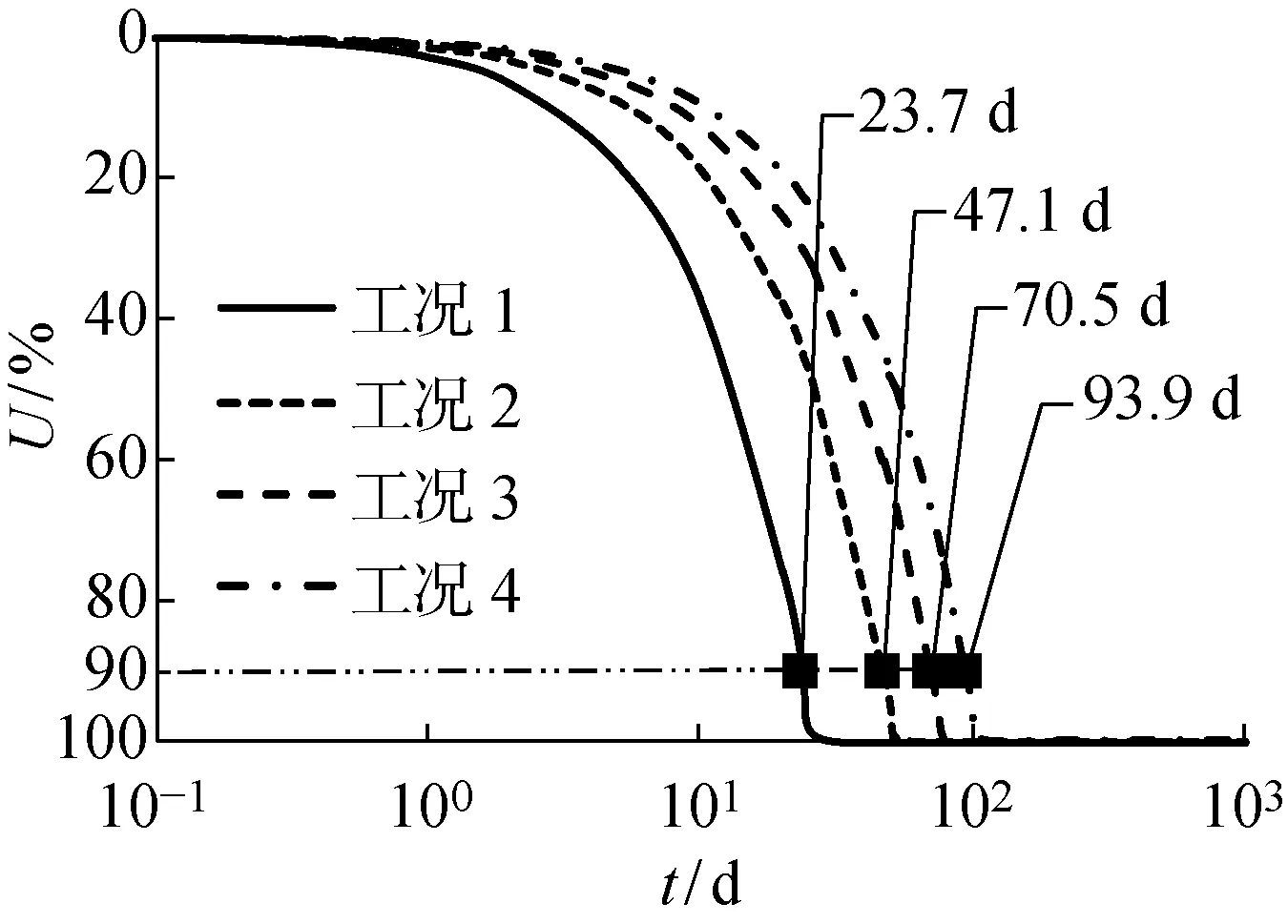
图3 4种工况下砂桩复合地基固结度的时程曲线Fig.3 Time history curves of consolidation degree of sand pile composite foundation under four working conditions

可以看出，沉井接高节数越多，加荷历时越长，砂桩复合地基的固结速率越慢.不考虑桩体内径向渗流时，4种工况下分别历时23.7、47.1、70.5及93.9 d，复合地基固结度可达到90%，地基固结已基本完成.

2.2.2砂桩置换率对砂桩复合地基固结度的影响 根据规范[14]，砂桩置换率主要通过砂桩内部径向渗流影响复合地基的水平向固结度，因此，探讨砂桩置换率的影响时需要考虑桩体内径向渗流.卢萌盟等[23]基于外部荷载瞬时施加且附加应力沿深度均匀分布的条件，推导了考虑桩体内径向渗流的复合地基总固结解：

(2)

本工程中实际砂桩置换率为36%，另取10%、20%和50%的砂桩置换率作对比分析.假设4节沉井接高瞬时完成，且地基中附加应力沿深度均匀分布，根据式(2)计算得到4种砂桩置换率下砂桩复合地基固结度的时程曲线，与规范方法进行对比，结果如图4所示(图中将卢萌盟方法标记为“卢”，规范方法标记为“规”，m为砂桩置换率).

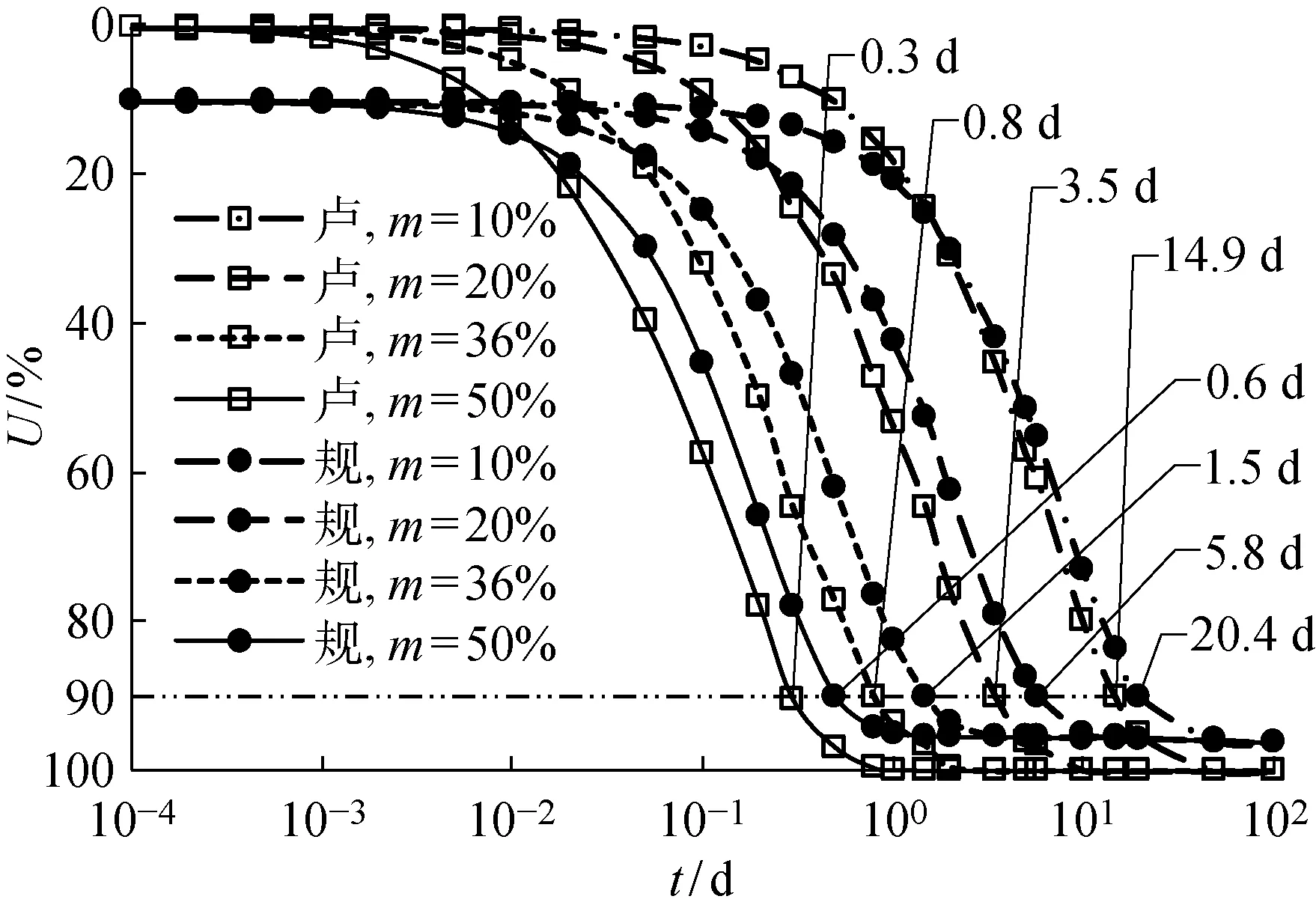
图4 4种砂桩置换率下砂桩复合地基固结度的时程曲线Fig.4 Time history curves of consolidation degree of sand pile composite foundation at four replacement rates of sand pile

可以看出，砂桩置换率越高，砂桩复合地基的固结速率越快.基于卢萌盟方法，沉井接高瞬时完成时，4种砂桩置换率下分别历时14.9、3.5、0.8及0.3 d，复合地基的固结度可达到90%.按照规范方法，4种砂桩置换率下分别历时20.4、5.8、1.5以及0.6 d，复合地基的固结度可达到90%，两者结果基本接近.

可以发现，砂桩置换率为36%且4节沉井接高的条件下，考虑沉井分节接高(忽略桩体内径向渗流)的复合地基历时93.9 d固结度达到90%，而假定沉井接高瞬时完成(考虑桩体内径向渗流)的复合地基仅历时0.8 d，两者固结速度相差较大.沉井接高的施工时间和砂桩内部径向渗流均是砂桩复合地基固结度的重要影响因素.

3 考虑固结影响的砂桩复合地基承载 特性

3.1 不考虑固结的砂桩地基承载力

3.1.1桩土面积比法 桩土面积比法的计算思路通常是先分别确定桩体的承载力和桩间土的承载力，然后根据面积比例叠加这两部分承载力得到复合地基的承载力.

龚晓南[24]提出了计算复合地基极限承载力的桩土面积比法公式：

Pcf=k1λ1mPpf+k2λ2(1-m)Psf

(3)

式中：Pcf、Ppf及Psf分别为复合地基、单桩及天然地基极限承载力；k1为反映复合地基中桩体实际极限承载力与单桩极限承载力不同的修正系数；k2为反映复合地基中桩间土实际极限承载力与天然地基极限承载力不同的修正系数；λ1为复合地基破坏时，桩体发挥其极限强度的比例，称为桩体极限强度发挥度；λ2为复合地基破坏时，桩间土发挥其极限强度的比例，称为桩间土极限强度发挥度.

散体材料桩的极限承载力主要取决于桩周土体所能提供的最大侧限力.在荷载作用下，散体材料桩体发生鼓胀，桩周土进入塑性状态，因此单桩极限承载力可通过桩间土侧向极限应力计算[25].其一般表达式为

Ppf=σrukp

(4)

式中：σru为桩侧土体所能提供的最大侧限力；kp为桩体材料的被动土压力系数.

计算σru时采用Wong方法[17]：

(5)

式中：kps为桩间土的被动土压力系数；σs为桩周土表面荷载；cu为桩周土不排水抗剪强度.

天然地基的极限承载力可采用太沙基地基极限承载力的公式[26]：

Psf=0.5γbNγ+csNc+qNq

(6)

式中：γ为天然土体重度；b为基础宽度；cs为天然土黏聚力；q为作用于基础两侧的均布荷载；Nγ、Nc及Nq为地基承载力系数.

将式(5)代入式(4)，并结合式(6)与式(3)，得到不考虑固结的砂桩地基承载力桩土面积比法表达式：

k2λ2(1-m)(0.5γbNγ+csNc+qNq)

(7)

3.1.2桩土应力比法 规范[15]规定，散体材料桩复合地基承载力应按下式计算：

Pspk=[1+m(f-1)]Psk

(8)

式中：Psk为处理后桩间土承载力特征值；f为复合地基桩土应力比，按地区经验或试验确定.

将复合地基承载力特征值和桩间土承载力特征值同时乘2倍安全系数得极限承载力：

Pspf=[1+m(f-1)]Psf

(9)

将式(6)代入式(9)，得到按规范计算的不考虑固结的砂桩地基承载力桩土应力比法表达式：

Pcf2=[1+m(f-1)]

(0.5γbNγ+csNc+qNq)

(10)

3.2 考虑固结的砂桩地基承载力增量

对于黏土，不排水抗剪强度指标φu=0，当采用不排水抗剪强度指标进行地基承载力验算时，可用不排水抗剪强度τu替代cu[5].当考虑固结引起的地基承载力增长时，式(6)可改写为

k2λ2(1-m)[0.5γbNγ+

(τu+Δτ)Nc+qNq]

(11)

式中：Δτ为抗剪强度增量.

由固结引起的复合地基承载力增量为

(12)

沈珠江[27]提出了有效固结应力法及相应的强度增长计算公式：

Δτ=U0Δσtanφcu

(13)

式中：U0为天然土体固结度；Δσ为附加应力；φcu为固结不排水试验得到的内摩擦角.

将式(13)代入式(12)，得基于桩土面积比法，由固结引起的砂桩复合地基承载力增量表达式：

U0Δσtanφcu

(14)

同理，可得到基于规范建议的桩土应力比法，由固结引起的砂桩复合地基承载力增量表达式：

ΔPcf=[1+m(f-1)]NcUΔσtanφcu

(15)

3.3 沉井基础下考虑固结的砂桩复合地基承载特性

3.3.1基于4种工况的复合地基承载特性分析 基于表2中的4种工况，不考虑桩体内径向渗流，首先由式(1)计算砂桩复合地基的固结度，然后分别代入式(7)和(10)得到基于桩土面积比法和基于规范建议桩土应力比法的砂桩复合地基初始承载力，同时代入式(14)和(15)，得到基于两种方法考虑固结的砂桩复合地基承载力时程曲线，结果如图5和表3.表3中：P0、P0.4、P0.7及P1分别为4种工况下固结度分别达到0、40%、70%及100%时的砂桩复合地基承载力.

表3 不同固结度时的地基承载力Tab.3 Bearing capacity of foundation at different consolidation degrees

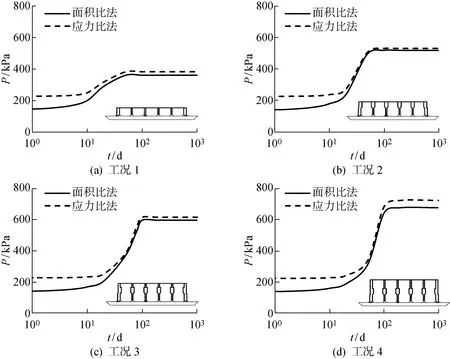
图5 4种工况下砂桩复合地基承载力对比Fig.5 Comparison of bearing capacity of sand pile composite foundation under four working conditions

可以看出，4种工况下面积比法和应力比法计算得到的复合地基承载力时程曲线较接近，初始承载力(即不考虑固结的承载力)相差60%，固结完成时两者相差2%～7%，差距明显缩小.由于未考虑桩体内径向渗流，承载力增长速率较实际情况更慢.

两种方法初始承载力均小于地基实测的天然承载力402.2 kPa，偏于保守.固结度达到40%时，两种方法计算承载力依然低于天然承载力.固结度达到70%时，工况3和工况4的承载力已超过天然承载力.固结完成时，除工况1外，最终承载力均超过天然承载力，其中工况4基于面积比法和应力比法固结完成时最终承载力分别为675 kPa和724 kPa，较天然承载力分别提高68%和80%.显然，固结引起的砂桩复合地基承载力增量不可忽视，尤其在沉井基础工程中，估算的地基承载力和实际值偏差不宜过大，否则可能因地基承载力过大发生沉井滞沉或地基承载力过小导致沉井突沉、偏沉等问题.

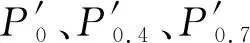
表4 不同砂桩置换率下的地基承载力Tab.4 Bearing capacity of foundation at different replacement rates of sand pile

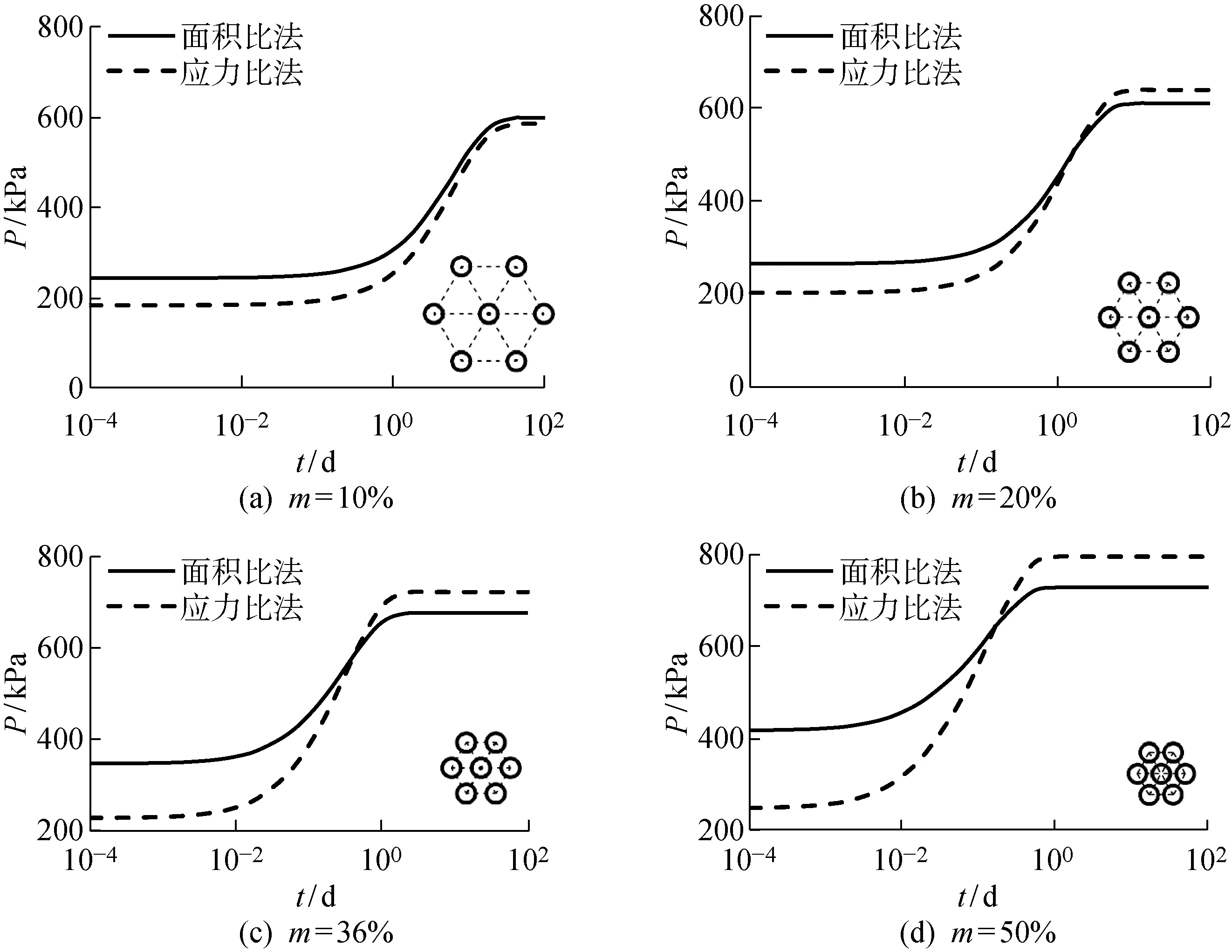
图6 4种砂桩置换率下砂桩复合地基承载力对比Fig.6 Comparison of bearing capacity of sand pile composite foundation at four replacement rates of sand pile

可以看出，4种砂桩置换率下面积比法和应力比法计算得到的复合地基承载力时程曲线较接近，初始承载力相差33%～66%不等，固结完成时两者相差2%～9%，差距明显缩小.此外，由于假定沉井接高瞬时完成，地基承载力的增速较实际情况更快.

综上，当固结度低于70%时，面积比法计算的复合地基承载力较应力比法更大，并且随着砂桩置换率提高差距增大.当固结度超过70%后，两种方法计算的承载力差距不大.考虑工程安全，推荐采用基于桩土应力比法的承载力算法.

4 结论

(1) 沉井的接高施工时间、砂桩内部径向渗流和砂桩置换率是砂桩复合地基固结度的重要影响因素.不考虑砂桩内部径向渗流时，沉井接高节数越多，加荷历时越长，砂桩复合地基的固结速率越慢.假定沉井接高瞬时完成时，砂桩置换率越高，砂桩复合地基的固结速率越快，与规范结果相近.

(2) 基于桩土面积比法和桩土应力比法考虑固结影响的砂桩复合地基承载力计算结果接近.沉井不同接高工况下，若不考虑砂桩体内径向渗流，基于桩土面积比法和桩土应力比法考虑固结影响的砂桩复合地基初始承载力相差60%，固结完成时相差2%～7%，差距明显缩小.假设沉井接高瞬时完成的条件下，4种砂桩置换率下两种方法计算得到的复合地基初始承载力相差33%～66%，固结完成时两者相差2%～9%.

(3) 当固结度高于70%时，两种方法计算的承载力差距不大.当固结度低于70%时，基于桩土面积比法计算的承载力较桩土应力比法结果更大，并且随着砂桩置换率提高差距增大.考虑工程安全，推荐采用基于桩土应力比法的计算方法.