孤立波和海流作用下单桩基础局部冲刷及保护的数值分析

黎蔚杰，张 琪，廖晨聪，周香莲，刘晨晨

(上海交通大学 海洋工程国家重点实验室； 土木工程系， 上海 200240)

随着海上风电场的发展和建设，近海地区建造了许多的海上桩基础.桩基的存在改变了周围的局部流场，导致桩基周围发生局部冲刷.随着冲刷深度的增加，桩的埋置深度减小，进一步降低了桩基的安全性甚至引起上部结构物的塌陷.因此，有必要研究海洋环境荷载作用下桩基周围冲刷机理.

近年来，国内外学者对桩基周围的局部冲刷问题进行了大量的研究.Ma等[1]通过实验的方法研究了潮流作用下群桩基础的冲刷规律，考虑了在单向水流作用和潮流作用下典型的哑铃型桩群的局部冲刷特性.Xu等[2]通过水槽实验研究了孤立波作用下桩式防波堤周围的冲刷规律，考虑了孤立波波高和局部水深对最大冲刷深度及最大沉积高度等的影响.刘红军等[3]通过实验的方法研究了局部冲刷对海上风机承载性能的影响.漆文刚等[4]建立桩基-土的数值模型研究了冲刷对海上风机单桩桩基础水平承载特性的影响.Baykal等[5]建立了三维数值模型，研究了波浪作用下圆柱桩周的冲刷和回填过程，结果表明，波浪作用下海床的冲刷和回填主要是由桩后的尾涡控制.段玮玮等[6]通过水槽实验研究了波浪作用下桥梁基础冲刷防护装置对桩周局部冲刷的影响，结果表明，桩周最大冲刷深度与水深和护圈直径成反比关系.Petersen等[7]通过一系列实验研究桩周围冲刷保护层自身的边缘冲刷过程，结果表明，平衡冲刷深度与桩的直径以及冲刷保护层的宽度与厚度之比成正比.

目前，已有一些关于波和水流联合作用下桩基周围冲刷的研究，但很少有人研究孤立波和海流作用下桩基周围的冲刷机理.本文建立了包含单桩-海床-波和流的三维数值模型，研究在孤立波和海流共同作用下位于倾斜海床中的桩周围的冲刷过程.数值结果表明该模型可以很好地模拟桩基局部冲刷.在此基础上，通过将不同波高的孤立波和不同的流速进行组合，研究波流共同作用下桩周围局部冲刷发展的规律，探讨了最大平衡冲刷深度以及冲刷坑形态变化的发展规律.另外，通过设置防冲刷层，研究冲刷保护层在冲刷过程中的作用.

1 计算模型和数值方法

1.1 水动力模型

流体运动的控制方程为N-S方程，包含描述流体运动的连续性方程和动量方程.其表达式为

(1)

(2)

式中：u、v及w分别为流体x、y及z方向的速度；φF为流动流体的体积分数；Ai分别为x、y、z方向上流动流体的面积分数(i=x，y，z)；ρ为流体密度；pw为平均动水压力；gi分别为x、y、z方向的重力加速度；fi分别为x、y、z方向上流体的黏滞力加速度.

1.2 湍流模型

为了准确地模拟流场和桩基的相互作用，采用 RNGk-ε湍流模型对桩周局部冲刷进行了研究[8]，湍流模型的表达式为

Te+Be+Dke-εt

(3)

(4)

式中：t为时间；ke为与湍流速度波动相关的湍流动能；Te为由于速度梯度引起的动能产生项；Be为浮力引起的湍流动能产生项；εt为湍流动能耗散率；Dke和De为与Ai、φF以及扩散系数等参数相关的扩散项;D1,D2和D3为无量纲参数，其中D1和D3默认值分别是1.42和0.2;D2是通过ke和Te计算而来，其表达式为

(5)

1.3 泥沙输运模型

泥沙输运模型通过对沉积物侵蚀、移送和沉积的预测，模型整个冲刷过程.泥沙的启动和沉积方程如下[9]：

(6)

(7)

(8)

式中：ψ为流场和床面的夹角；βc为床面倾斜角；φi为泥沙休止角；ρ为水的密度；di为泥沙颗粒的直径；ρi为泥沙颗粒的密度；vf为水的运动黏度.

泥沙的悬移质运动的控制方程为

(9)

式中：Cs,i为悬移质的质量分数；us,i为悬移质的运输速度；Df为扩散系数.

泥沙的推移质输运描述泥沙颗粒在流体作用下沿海床表面的滚动、跳跃和滑动的运动过程，Flow-3D采用Meyer-Peter Muller公式[10]计算推移质运输速度ubed,i，控制方程如下:

(10)

式中：qb,i为单位宽度的推移质运输速率

(11)

φb,i为组成海床的不同泥沙种类所占的体积分数；fb为泥沙临界填充分数；ρf为对应泥沙的密度.

通过输沙平衡来计算床面高程h的变化，表达式如下：

(12)

式中：p′为泥沙孔隙率.

1.4 波浪理论

波浪模型中，孤立波的波面高度Hw方程和波速c方程基于Munk的理论[11]，表达式为

(13)

c=u0+c0

(14)

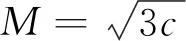
2 边界条件和网格

数值模型的边界条件如图1所示.模型入流边界选择波浪边界，海床底部设置为壁面边界，模型的出口设置为出流边界，模型的两侧边界设置为对称边界，模型的顶部采用压力边界来模拟大气压环境.为了防止波浪的反射，在出口端设置消波层.

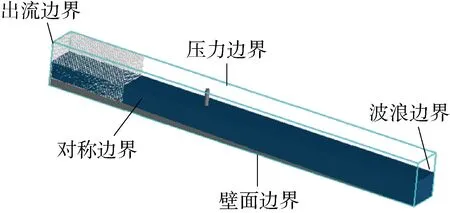
图1 数值模型的边界条件Fig.1 Boundary conditions of numerical model

采用流体体积(VOF)法捕捉流体表面的位置，采用浸没边界(FAVOR)法方法对三维数值模型进行网格划分，每一个单元都包含了所有变量的信息.在每一个时间步长范围内都计算了描述沉积物的面积分数Ai和体积分数φF，以此来反映沉积物冲刷模型几何形状的改变.与传统的有限差分法相比，避免了对结构物边界拟合程度不高的缺点，同时网格的数量大大减少，节约了模型的计算时间.

3 模型验证

在进行数值研究之前，对单桩周围局部冲刷进行验证.参考Roulund等[12]的物理模型实验建立了数值模型，光滑圆柱的直径为0.1 m，水深0.4 m，平均入流速度为0.46 m/s.设置沙床厚度为0.2 m，沙床中砂石平均粒径为0.26 mm，密度为 2 650 kg/m3，休止角为32°.

图2是圆柱迎水侧冲刷深度计算值随时间变化的关系和实验结果的对比，图中S为冲刷深度.可以看出，冲刷深度的数值模拟结果和实验数据拟合较好.因此，本文建立的圆柱冲刷三维数值模型能较好反应桩周的实际冲刷情况.

图2 圆柱迎水侧冲刷深度数模拟值与实验数据的对比图Fig.2 Comparison of simulated values and experimental data of scour depth at the upstream side of the pile

4 数值结果和讨论

如图3所示，数值模型的尺寸为长250 m，宽16 m，z方向高度为20 m.笛卡尔坐标的原点位于倾斜海床的起点(x=0).海床的倾斜度m为1∶50，由直径为0.5 mm和0.85 mm两种不同直径的泥沙颗粒组成.泥沙颗粒的密度为ρs=2 650 kg/m3，临界希尔兹参数为θd,i=0.048，夹带系数设置为0.018.推移质系数根据默认值设置为8.0，泥沙的休止角为30°，桩的直径为2 m.桩周附近网格尺寸在x和y方向为 0.2 m，其他区域是0.4 m，海床的网格尺寸为0.15 m.

图3 数值模型整体示意图Fig.3 Integrated sketch of numerical model

4.1 孤立波和流共同作用对冲刷的影响

图4所示为单纯水流作用、单纯孤立波作用及孤立波和水流共同作用下桩周最大冲刷深度随时间变化的曲线图.可以看出，孤立波和水流共同作用下的冲刷深度发展速度快于单独水流作用或单独波浪作用，最大冲刷深度大于波浪和水流单独作用下的最大冲刷深度的线性叠加.在孤立波还未抵达桩前的时候，冲刷深度的发展趋势和单纯流作用下一致，在孤立波抵达桩前，冲刷深度曲线在短时间迅速下降.

图4 单纯孤立波、水流、波流共同作用下冲刷深度变化图Fig.4 Changes of scour depth under the action of wave-only, current-only, and wave-current

4.2 海床倾斜、孤立波波高对冲刷深度的影响

图5为相同条件下(波高H=4 m,流速v=2 m/s)位于水平和倾斜海床上桩周冲刷深度随时间的变化过程，从图中可以看出，倾斜海床桩周最大冲刷深度大于水平海床桩周最大冲刷深度.

图5 水平海床和倾斜海床下桩周最大冲刷深度变化图Fig.5 Changes of maximum scour depth around pile located on flat seabed and inclined seabed

图6为不同孤立波波高下桩周海床冲刷高程图.可以看出，不同波高下，虽然局部冲刷的最大冲刷深度都出现在桩前侧45° 的方向，但是桩周冲刷坑的形态有很大的不同.同时，孤立波波高越大，冲刷深度越大，冲刷范围也更广泛.

图6 桩周海床冲刷高程图Fig.6 Bed elevation contours around pile

4.3 保护层对冲刷深度的影响

如图7所示，添加保护层的数值模型的尺寸为 35 m×16 m×7 m，桩的直径1.5 m.在桩周设置冲刷保护层，保护层形状为直径6 m，高度为1 m的圆柱，为了精确地捕捉到保护层形状的变化，冲刷保护层区域附近网格尺寸x和y方向为0.08 m.海床的厚度为3 m，最小尺寸为0.1 m.流边界处水流速度为2 m/s.其余冲刷参数设置保持不变.

图7 数值模型整体示意图(m)Fig.7 Integrated sketch of numerical model (m)

图8所示为添加桩基保护层后单桩桩周的三维冲刷坑形态图.从图8(a)可以看出，保护层的存在使得海床在一开始并没有发生冲刷，随着时间的发展，保护层先被侵蚀，此时海床开始发生冲刷，但是冲刷坑的发展非常缓慢(图8(c)、8(d)、8(e))，最终残余的保护层围绕在桩的周围，且冲刷坑的形态基本不变，而桩基后方的沙堆进一步向下游方向移动，形成较长的沙纹(图8(f)).

图8 单桩桩周的三维冲刷坑形态随时间的冲刷过程Fig.8 Scour process of three-dimensional scour pit shape around a single pile over time

图9所示为t=500 s时三维桩周冲刷坑形态和桩周海床冲刷高程图.比较图9(b)、9(d)与图9(a)、9(c)可以看出，设置保护层后桩基周围的冲刷坑形态发生明显的改变，且海床的最大冲刷深度明显减少，为0.43 m(图9(d)，海床的实际冲刷深度要减去保护层的厚度1 m)， 这表明保护层对单桩局部冲刷的影响较大.

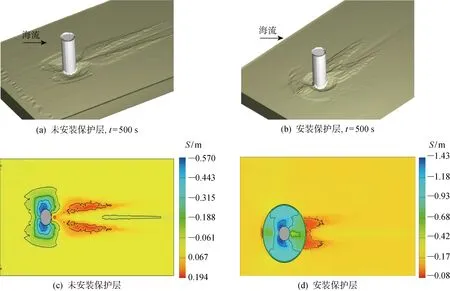
图9 t=500 s时三维桩周冲刷形态和桩周海床冲刷高程图Fig.9 Three-dimensional scour morphology and elevation of seabed scour around pile at t=500 s

为了进一步研究保护层对冲刷的影响，对3种不同粒径的保护层进行了计算.图10所示为3种情况下的桩周最大冲刷深度随时间变化的曲线图，图中百分数为碎石质量分数.可以看出，随着组成保护层碎石粒径的增大，桩周的最大冲刷深度也明显减少.这是因为保护层可以在一定程度上改变桩周附近流场，降低近海边界层的水流速度，使得泥沙颗粒难以被起动和冲刷，这种保护效果随着保护层粒径增大更加明显.

图10 不同粒径的保护层下桩周局部冲刷的计算结果Fig.10 Calculation results of local scour depth under scour protection at different grain sizes

5 结论

本文研究在孤立波和水流共同作用下，位于倾斜海床上的桩基周围的局部冲刷和冲刷保护措施.分析了孤立波波高和海床的倾斜对桩周局部冲刷最大冲刷深度和冲刷坑形态的影响.在此基础上，研究了设置冲刷防护措施对冲刷深度的影响.主要结论如下:

(1) 孤立波和水流共同作用下桩周的冲刷深度大于波浪和水流单独作用下的线性叠加.

(2) 在相同的波浪流条件下，倾斜海床桩周最大冲刷深度大于水平海床桩周最大冲刷深度.

(3) 为了减少冲刷深度，提高海床的抗冲刷能力，可以在桩周设置冲刷防护(砾石、石块等)，保护层的粒径大小对冲刷深度影响较大.