小学数学深度学习中
2021-06-28黄小宇
黄小宇
摘 要:“大情景、真问题”“深度学习、高阶思维”是这两年听得最多的关键词。深度学习的本质在于深度思考,而“教”建立在“学”的基础上。在深度学习指导下学生是学习的主人,培养学生提问题的能力,发展创造性思维和探究精神,培养创新意识和应用意识。在此,文章以发现的“巴普斯定理”为视角,谈一谈引领学生深度学习的思考与实践。
关键词:深度学习;巴普斯定理;面动成体;线动成面
【中图分类号】G623.5 【文献标识码】A 【文章编号】1005-8877(2021)13-0011-02
【Abstract】“big situation,real problem”,“deep learning,high-level thinking” are the key words I have heard most in the past two years. The essence of deep learning lies in deep thinking,and “teaching” is based on “learning”. Under the guidance of deep learning,students are the masters of learning,cultivate their ability to ask questions,develop their creative thinking and spirit of inquiry,and cultivate their consciousness of innovation and application. Here,the article takes the discovered “Baps theorem”as the Angle of view,talks about the thinking and practice that leads the student to study deeply.
【Key words】Deep learning;Baps theorem;Plane dynamic adult;Line dynamic plane.
深度学习是指在理解学习的基础上,学习者能够批判性地学习新的思想和事实,并将它们融入原有的认知结构中,能够在众多思想间进行联系,并能够将已有的知识迁移到新的情境中,作出决策和解决问题的学习。——黎加厚。
“巴普斯定理 ”是高中数学才学习的内容,然而在小学数学的课堂上却真实的发现了,教师在深度学习理论的指导下,带领学生一起探究各几何图形的体积和面积各自之间的内在联系,学生们经历猜测、探索、验证、应用等一系列的数学学习过程,自行发现体积、面积的通用计算方法。感受到数学知识内在统一的魅力,提高了学生发现问题、提出问题、解决问题的能力,提升了学生的数学素养。
1.“面动成体”。从“旋转门”打开的奇妙探索之旅
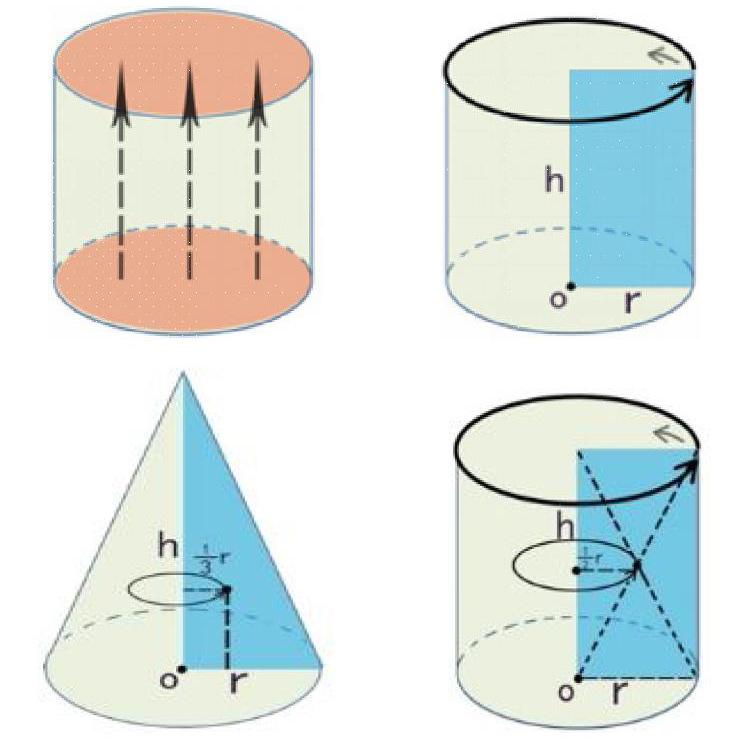
在教学圆柱体体积时,我问:“你猜测一下圆柱体的体积应该是怎样计算的?”学生A说:“根据“面动成体”,可以把圆柱体看着是一片片的薯片叠加而成的,这样自然就是一片圆形薯片的底面积乘以高就是圆柱体的体积。”这想法和我们将圆柱体经过切割转化为等底、等高、等体积的长方体的推导过程还是有所不同。经过圆柱体体积的推导学习后学生们发现得到的公式:圆柱体体积=底面积×高。验证了学生A的猜想。这时,学生B说道:“那酒店门口的旋转门,也可以看成是一个长方形玻璃门绕中轴旋转一周得到的圆柱体,这也是“面动成体”啊?是否圆柱体的体积也可以是一个长方形的面积乘以这个长方形旋转一周后圆的周长呢?”或许是受到学生A“面动成体”的影响,学生的思路一下被打开了。确实这种“面动成体”形成的圆柱体也是通过图形运动完整得到的圆柱体,学生的直觉激发了我,或许这里隐藏着圆柱体体积推导的另外一种思路?我大肆赞赏学生B创造性思维的同时,也抱着严谨的态度对学生们说:“大家可以按照学生B的思路回去后好好研究一下是否也可以得到圆柱体的公式呢?不过一切还是要以事实来验证。”第二天,课上很多孩子研究后反馈出来的结果居然是:圆柱体的体积=底面积×高×2!理由是:长方形的面积是S=rh,底面周长是C=2πr。因此:圆柱体体积V=2πr2h。这结果显然是错的!那问题出在哪里呢?这时,有学生回答道圆柱体如果是像薯片一样一片片叠加得到的,这样底面积是做平移运动,上面的每一个点走过的路程是一样长的,也就是高。而旋转门是一个长方形绕中轴旋转得到,这个长方形上的每一个点走过的路程是不一样的,最外面那条边走过的路程是圆的底面周长C=2πr,可是里面那条边也就是中轴只是在原地旋转根本都没有动啊!也就是说这个长方形上的每一个点在旋转时走过的路程是不一样的,所以推导出来的体积扩大2倍了!确实学生的话语切中要害!那究竟该用长方形的哪个点来代表这个长方形走过的路程才最公平呢?经过讨论大家一致同意应该用长方形的中间一点也就是两条对角线的交点来代表长方形上的每一个点最公平,它到中轴的距离也就是整个长方形每个点到中轴距离的平均值!因此这样它的半径就是以原来底面半径的一半,所以推导出圆柱体的体积就是长方形的面积乘以底面半径一半旋转一周的周长得到V=πr2h!换个思路一样可以推导出圆柱体的体积,确实很巧妙!也有学生觉得这样推导不是很麻烦吗?为何要研究这种方法呢?这时又有学生问到这样的思路是否可以推导出圆锥的体积公式呢?根据“面动成体”圆锥又是由什么图形运动产生的呢?一石激起千层浪,这一系列的问题,激发了孩子们强烈的探索新知的欲望,确实圆锥的体积公式我们是通过实验法得到的,如果能够用这种方法推导出圆锥的体积公式,那岂不是一件振奋人心的事情?经过讨论,大家一致認为圆锥是通过一个直角三角形绕一条直角边也就是圆锥的高旋转一周得到的。关键是要以三角形的哪个点来代表整个三角形所有点绕中轴旋转一圈的走过的路程才公平?才是它们的平均值?受圆柱体长方形的中点启发,大家一致认为要以三角形三边中线的交点也就是三角形的重心为代表最合理。通过老师的引导和分析这个交点到中轴的距离可以证明出正好是底面半径的三分之一!因此可以得到圆锥的体积就是这个三角形的面积乘以三角形重心旋转一周的周长。也就得到了圆锥的体积公式:V=πr2h/3。根据“面动成体”这一看似简单的一句话,居然可以不需要通过微积分及高等数学的方法来得到圆锥的体积公式,对孩子们而言带来了强大的成就感!这巧妙的思路同样的也激发起孩子们强大的求知欲,那怎样求球的体积呢?学生发现球也是由一个半圆绕中轴旋转一周得到的,半圆的面积我们已经会求了,关键是这个半圆上的哪一个点来代表这个半圆旋转一周的路程最合理呢?虽然孩子们根据现在的知识还是无法探索出这个点到中轴的距离和半圆半径之间的关系,但是这种“面动成体”通过旋转的方法得到的三维物体的体积公式推导居然可以适用于圆柱体、长方体、圆锥体、甚至球体。学生们感到非常的惊讶!对“面动成体”有了更深刻的认识。
2.“线动成面”唤起三维和二维之间的联系和统一
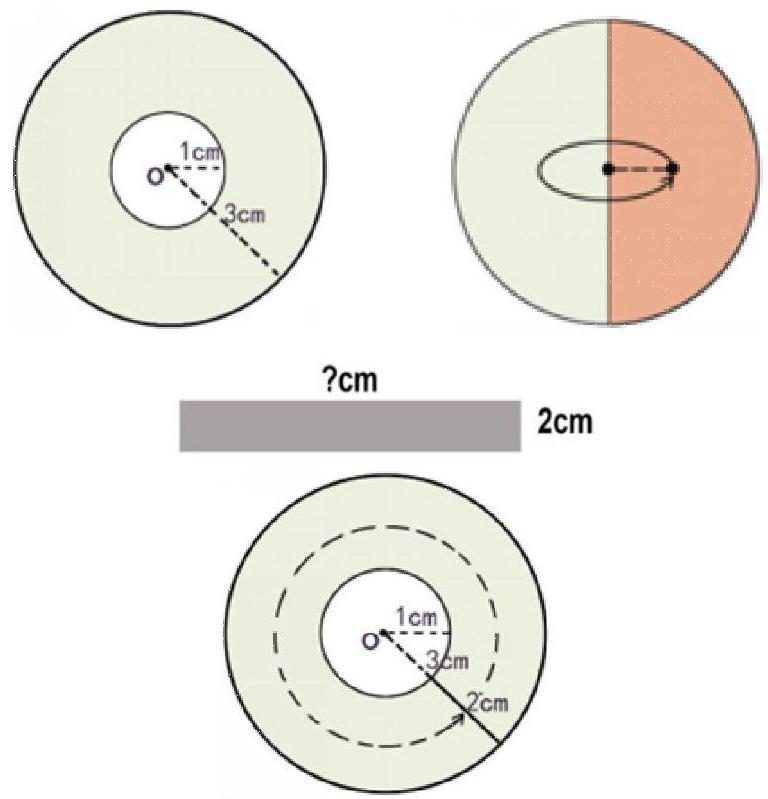
回到半年前在一次课堂上出现的“插曲”。记得在教学《圆》这单元,求环形面积:“一个环形,内圆半径是1cm,外圆半径是3 cm,求环形面积是多少?”有部分学生会出现典型的错法:3.14×(3-1)×(3-1)。所以我在教学时便反复强调计算环形面积时一定要用大圆的面积减去小圆的面积,千万不能第一步就用大圆的半径去减小圆的半径,如果出现这步,那么后面就绝对错。因为环形的面积不等于以他们半径差的结果为新半径的圆的面积!其实我的分析没有错,强化正确的做法,确实能提高解题的正确率。当自己还在为帮学生“明辨是非”的解析感到自豪时,有位学生对我说:“老師,我觉得环形面积的求法可以用大圆半径减去小圆半径的方法来计算,你看环形的这一圈宽也就是半径差都一样,这一圈面积不是也可以拼成一个长方形吗?所以我就是用半径差去乘外圆的周长来求环形的面积。”听了他的分析,我眼前一亮,觉得他的思维很独特,学生的直觉思维往往有他的道理,但我又感觉他的想法似乎有点问题。因此我在肯定他独特的想法的同时也对他说:“你的想法很好,老师很欣赏,但你说的用半径差去乘外圆的周长来求环形的面积,我有不同的想法,为什么不行用半径差去乘内圆的周长来求环形的面积呢?这样两个答案不就不一样了吗?看来我们需要静下来用计算来进行验证。”于是课堂上孩子们兴趣盎然和我共同的计算研究,终于我们发现用半径差去乘内、外圆周长的平均数来求环形的面积和正常解法求环形面积的结果一样!
常规解法:3.14×3×3—3.14×1×1=28.26—3.14=25.12(平方厘米)
特殊解法:(3.14×3×2+3.14×1×2)÷2=12.56(厘米)
12.56×2=25.12(平方厘米)
这个案例是在学圆柱体积之前六年级上学期《圆》这单元中偶然发生的一次插曲,当时没有深入研究只是浅谈辄止。这次学生经历了圆柱体、圆锥体体积奇特的推导过程后恍然大悟,根据“面动成体”自然联想到“线动成面”。这个环形面积不也可以看成半径差为2厘米的线段绕圆心O走一圈所围合而成的图形吗?那这条线段以哪个点走过的路程为标准才公平呢?自然是这半径差的中点!因此这个环形的面积就是:半径差的中点走一圈的路程乘以半径差2厘米。列式:3.14×2×2×2=25.12(平方厘米),看来三维图形的“面动成体”一样可以运用在二维图形的“线动成面”这里。大家为自行发现的这个原理欢声雀跃,这是否是自己的独创呢?后来上网一查才知道原来这叫巴普斯定理:在一平面上取任一闭合区域,其面积为S,使它沿垂直于该区域的平面运动形成一个体积为V的立体,那么这个立体图形的体积就等于质心所经路程 r 乘以区域面积。表达式为V=S·r。如果令某一长为L的曲线段,其长度为L,使它沿着垂直于它所在平面的方向扫过一个面积S,那么这个面积的大小就等于线段的质心移动的距离r乘以线段的长度。表达式为S=L·r。学生们虽然有些遗憾前人已经早于我们发现了这定理,但是通过探索能够深刻感受到这个定理能将所有几何里的面积和体积的计算方法统一了起来,包括长方形等图形面积都可以用这定理来解释,充分感受到数学的魅力以及探索数学的乐趣。
布鲁纳曾说过学习的实质是一个人把同类事物联系起来,学习就是认知结构的组织和重新组织。而深度学习是指在教师引领下,学生围绕具有挑战性的学习主题,全身心积极参与、体验成功、获得发展的有意义的学习过程。学生们经历了这次圆柱体、圆锥体的体积、环形面积奇特的推导过程,激发了学生探索数学的热情,这也给孩子们埋下一颗探索未知的种子,培养了学生的创新意识和应用意识。
参考文献
[1]孙双金.深度学习与批判性思维的研究[J].江苏教育,2019(01)
[2]马丽云.巴普斯定理及其应用[J].中学理科.综合,2018(01)
