基于互信息PSO-LSSVM的SO2浓度预测
2021-06-28金秀章
金秀章,李 京
(华北电力大学 控制与计算机工程学院,河北 保定 071003)
1 引 言
发展经济的同时,环保达标已经成为了一项重要指标[1]。近年来我国对使用火电机组的电厂SO2排放的要求[2]为小于35 mg/m3。所以,火电厂需要严格控制SO2排放,SO2浓度的检测也更需要达到准确、迅速以及对入口SO2浓度进行提前控制。
目前,由于测量SO2的仪器测量时间较长且火电厂的SO2测量仪的安装位置距烟气管道较远等原因,无法及时测得SO2值,使得存在煤燃烧后要经过一定延迟才会发现SO2浓度的变化,对脱硫作业以及提前喷浆控制都十分不利。因此,需要对SO2入口浓度进行预测,进行喷浆提前控制。
传统的SO2排放预测是通过CEMS仪表进行检测。这些仪表价格昂贵且需要人工安装以及硬件的维护,建设与维护费用较高。通过本文提出的软测量预测模型,预测精度贴近实际仪表测量值,可以节约建设成本与维护费用。
软测量技术是通过计算机,利用实际中易测量的辅助变量,对难测量或无法测量的主导变量进行预测[3]。软测量建模有基于机理建模法[4]、数模建模法[5]、回归分析法[6]、灰色预测法[7]、人工神经网络建模法(artificial neural network,ANN)[8]、支持向量机建模法[9]等。其中,在支持向量机分类法基础上发展出了最小二乘支持向量机(least squares support vector machines,LSSVM),预测结果的好坏,由LSSVM模型的参数决定。本文采用粒子群算法(particle swarm optimization,PSO)进行参数选取的优化,提高了模型的预测精度。
2 互信息理论
在机器学习中,信息熵(information entropy)常用来描述一个事物所包含信息量的多少,因此信息熵可以成为函数的优化目标或者方程式中参数选取的最佳值。信息熵的定义公式为:

(1)
若两个时间不相互独立,满足:
H(A,B)=H(A)+H(B)-I(A,B)
(2)
式中:I(A,B)为A与B之间的互信息量[10],表示A变量中含有B变量信息的多少或者B变量中含有A变量信息的多少。
事件中一个随机事件关于另一个随机事件的信息量称为互信息量,互信息量I(A,B)是定量地研究信息流通问题的重要基础。通常用事件A的后验概率p(A|B)与先验概率p(A)比值的对数表示互信息量,即:
(3)
同理,可以定义B对A的互信息量:
(4)
而p(AB)=p(A)p(B|A)=p(B)p(A|B),可得:
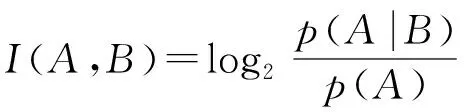
=I(A)-I(A|B)
=I(B)-I(B|A)
=I(A)+I(B)-I(AB)
(5)
算法性能的表现由评价函数决定,因此在互信息选择特征时该函数起着至关重要的作用。通常直接选取输出变量B与输入变量A互信息值作为评价指标,引入BIF算法进行评价,BIF算法第一步会将所有候选特征变量f进行其评价函数(J(f))计算,然后依据函数值大小按降序排序,最终选择前k个特征变量作为子集S。BIF算法的优点是效率高,因此它适用于高维数据处理中。其中BIF算法的评价函数如式(6)所示。
J(fi)=I(fi;c)
(6)
式中:fi为辅助变量;c为预测模型的主导变量。
这种算法最终能从较多辅助变量中筛选出与主导变量相关性最大的辅助变量,却未考虑到辅助变量之间的信息冗余。MIFS算法将惩罚因子引入了评价函数中,大大降低了辅助变量之间的信息冗余。MIFS算法的评价函数为:
(7)
式中:fi∈f为辅助变量;β为惩罚因子;Si∈S为已选变量。
利用式(7)的评价函数,既能筛选出与输出变量相关性最大的辅助变量,还剔除了辅助变量之间的冗余性,达到了辅助变量之间相关性最大、信息冗余性最低的目的。β越大,则评价函数反映出的辅助变量之间的信息冗余越多。
参数β的选取很大程度上影响MIFS算法选取辅助变量,而最小冗余最大相关性(minimum redundancy and maximum relevance, mRMR)算法很好地解决了β难以确定的问题。其评价函数为:
(8)
mRMR算法的具体步骤如下:
Step1: 初始化辅助变量中已选变量与未选变量的集合S和f。
Step2: 确定未选变量fi∈f,同时分别求得fi与主导变量c之间的互信息。
Step3: 确定第一辅助变量。用上述BIF算法,求得与主导变量之间的互信息,将辅助变量按互信息数值从大到小依次排列。
Step4: 贪心搜索。循环计算第一辅助变量fS与未选变量fi之间的互信息数值,依据评价函数J,将未选辅助变量中与第一辅助变量相关性最大的变量fi作为下一个变量;与此同时,f=f-{fi},S=S+{fi},继续循环,直到筛选的变量个数达到初始设置的变量个数n。
3 LSSVM理论
f(x)=WTφ(xk)+b+ek
(9)
式中:W∈Rdn;b∈R;ek∈R,k=1,2,…,n。
根据结果风险最小化原则,并引入最小二乘法,式(9)必须满足式(10):
(10)
式中:e为误差;γ为正则化参数。
依据拉格朗日法,可写成下式:

(11)
式中αk(k=1,2,…,n)为拉格朗日因子。
消除参数W和e后,有:
(12)
式中:y=[y1,y2,…,yn];l=[1,1,…,1];α=[α1,α2,…,αn];Ωkl=φ(xk)Tφ(xl);k=1,2,…,n。
寻找满足式(11)的α和b是LSSVM建模的目标。最小二乘支持向量机核函数定义公式为:
k(xk,xl)=φ(xk)Tφ(xl)
k(xk,xl)是Mercer约束条件的任意对称函数。引入核函数后的函数如式(13)。
(13)
核函数的选择对最小二乘支持向量机的预测有较大影响,但核函数选取至今没有好的方法及经验。径向基函数(RBF)、多项式函数和S函数等较为普遍使用,本文选用径向基函数(RBF)。
4 粒子群(PSO)理论
粒子群算法源于对鸟群中飞行动作的模仿[12],较遗传算法等寻优算法简单,可用来优化多种函数组合下的参数,从而寻找最佳工作参数。对于计算过程而言,使用粒子群算法首先需要初始化粒子群的各项参数,例如粒子的初始速度、位移及其决定的适应值等,然后进行迭代计算。迭代过程中,每个粒子都以2个最优值为标准框定自己的行进路线,1个是粒子本身所找到的目前最优解,该最优解将被粒子记录;剩下的1个粒子在所有种群中寻找到最优解。若粒子群间有相互通讯的方式,则各粒子都能寻找到自己所在的最优位置。其算法如下:
vij(t+1)=wvij(t)+c1r1j(t)(pij(t)-Xij(t))+
c2r2j(t)(pgj(t)-Xij(t))
(14)
Xij(t+1)=Xij(t)+vij(t+1)
(15)
式中各参数的含义如下:
1)i为第i个粒子,i=1,2,…,M。M是该群体粒子的总数,本文选取M=300。
2)j为各粒子中寻优的第j个参数。
3)w为惯性权值因子,其大小影响整体的寻优能力,为了保证其收敛到全局最优,避免出现早熟收敛,一般采用权值w在wmax与wmin之间线性递减的方法。本文选取wmax=0.9,wmin=0.4。
4)t为此时优化的代数。
5)vij(t)为第i个粒子在j维空间中的速度。
6)c1和c2为加速因子,本文中选取c1=1.7,c2=1.5。
7)r1j和r2j为相对独立的两个随机参数,其值变化范围在[0~1]之间。
8)pij(t)为粒子i的历史最优解的j维值。
9)pgj(t)=min{pij(t)}为各粒子在t时刻的历史最优解的j维值,即所有粒子在所优化的第j个参数中的历史最优解。
10)Xij(t)为粒子i处于j维空间的位置。
根据这2个方程,进行迭代计算动态更新粒子的位置和速度,搜索迭代过程中粒子的各个适应值的最优值,根据目标函数计算适应度值。整个搜索过程中获得的最佳方程解是全局最优解。当群体搜索到满足最小适应值的最优位置或者达到迭代次数之后即可结束计算。
5 入口SO2浓度预测模型的建立及仿真
对陕西某电厂所采样的数据进行优化处理后,利用互信息的方法筛选出辅助变量,并采用PSO算法对LSSVM的参数进行寻优,建立出SO2浓度的预测模型。
5.1 辅助变量的选择
本文通过机理分析[13],筛选出了36个辅助变量,其中主要有机组负荷、总煤量、总风量、石灰石浆液浓度、石灰石浆液循环泵电流等。通过互信息(mutual information,MI)和最大相关-最小冗余(mRMR)结合的方法,以预测模型的输出精度作为筛选标准来确定最终辅助变量的个数,建立了以入口SO2浓度为主导变量的预测模型。筛选出的变量有浆液循环泵电流、氧化风机电流、空预器含氧量等18个辅助变量作为模型输入。辅助变量及预测流程如图1所示。
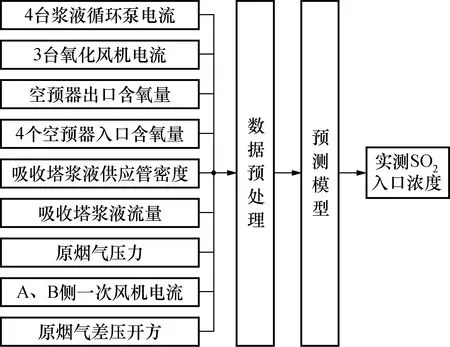
图1 SO2入口浓度排放模型结构图Fig.1 Structure diagram of SO2 inlet concentration emission model
5.2 数据预处理
在分析数据的相关性方面,采用皮尔逊(Pearson)相关性[14]分析变量的相关性,得出数据的相关性非常低,不能较好地作为模型辅助变量的输入。通过对10 000个样本进行分析,辅助变量与主导变量之间的相关性系数大都在0.5以下,很难确定出相关性较高的辅助变量。因此,本文采用互信息方法筛选辅助变量,从现场的36个辅助变量中最终筛选出18个辅助变量作为模型的输入,再通过mRMR方法[15]排列出与主导变量信息量最大的辅助变量,经过调试选出最合理的辅助变量。为了防止各辅助变量之间因数值差异过大而产生的样本间的相互影响,对数据进行了归一化和反归一化。对辅助变量进行皮尔逊相关性分析,相关性较大的辅助变量如表1所示。互信息筛选出的辅助变量如表2所示。
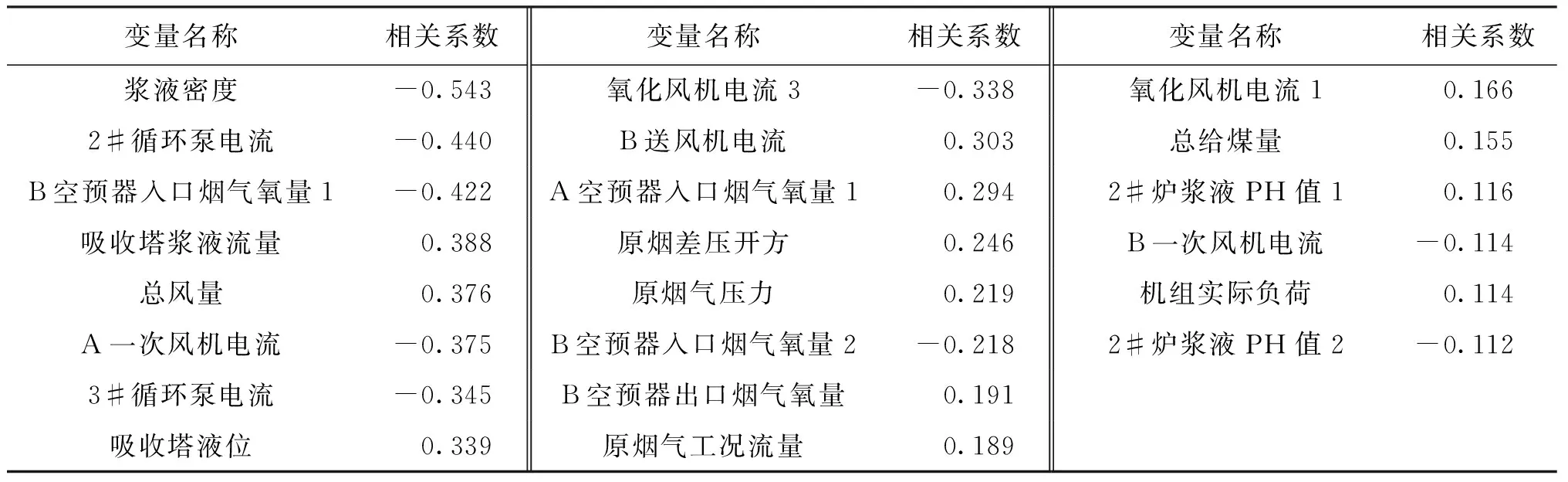
表1 皮尔逊相关性分析得到的相关性较大的辅助变量Tab.1 The auxiliary variables with high correlation were obtained by Pearson correlation analysis
火电厂锅炉的燃烧工作过程是一个非常复杂的过程,存在多变量、多耦合以及迟延滞后的问题,通过分析给煤量、总风量以及机组负荷等变量的变化与入口二氧化硫浓度变化之间的变化趋势做了时间序列的调整,通过调整入口二氧化硫浓度与辅助变量的时序进一步提升了模型的预测精度,调整时间为600 s。
5.3 预测结果分析
利用上述方法选取1 100组变负荷时的数据进行仿真预测实验,对800组采样间隔为1 s的数据进行训练,采用300组采样间隔为1 s的具有代表性的升负荷时数据进行预测。LSSVM的参数采用PSO算法进行寻优,LSSVM采用径向基函数RBF作为核函数;通过PSO算法得到模型的正规化参数δ2和核函数参数C,分别为37.140 7和128。利用模型LSSVM与PSO-LSSVM得出的预测结果如图2和图3所示。
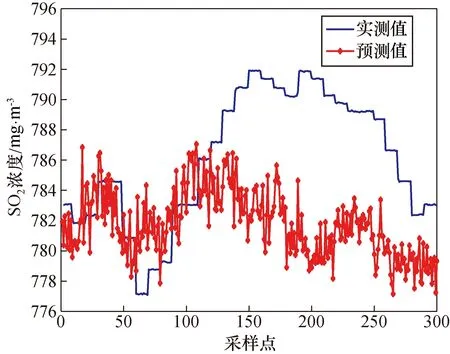
图2 Pearson LSSVM模型预测结果Fig.2 Pearson LSSVM model prediction results
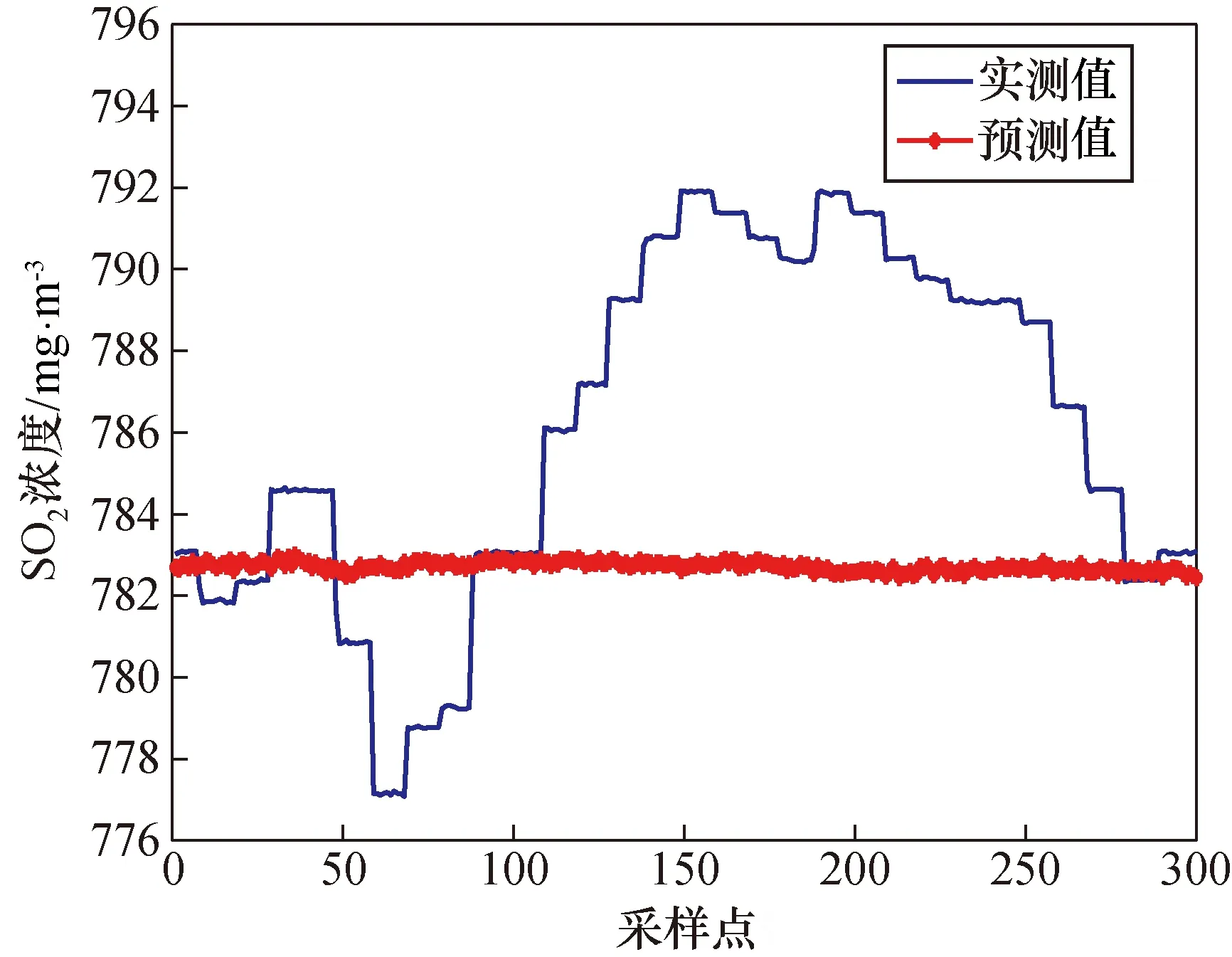
图3 Pearson PSO-LSSVM模型预测结果Fig.3 Pearson PSO-LSSVM model prediction results
利用互信息理论分析得出的辅助变量如表2所示,利用模型LSSVM与PSO-LSSVM得出的预测结果如图4和图5所示。

图4 互信息 LSSVM模型预测结果Fig.4 Mutual Information (MI) LSSVM model prediction results
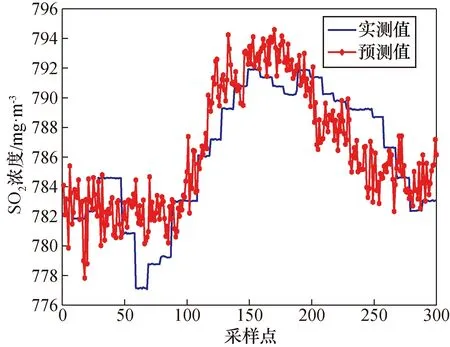
图5 互信息 PSO-LSSVM模型预测结果Fig.5 Mutual Information (MI) PSO-LSSVM model prediction results
经对比可以发现,基于互信息方法筛选出的辅助变量利用PSO算法进行参数寻优后的LSSVM模型相对于李龙等[16]提出的未寻优得到的LSSVM模型对SO2浓度的预测值更接近实际值,且均方根误差与最大误差均优于普通LSSVM模型。综合对比可以得出,基于互信息的PSO-LSSVM模型预测结果最好。各算法的均方根误差(RMSE)、平均相对误差(MRE)和最大误差(ME)如表3所示。
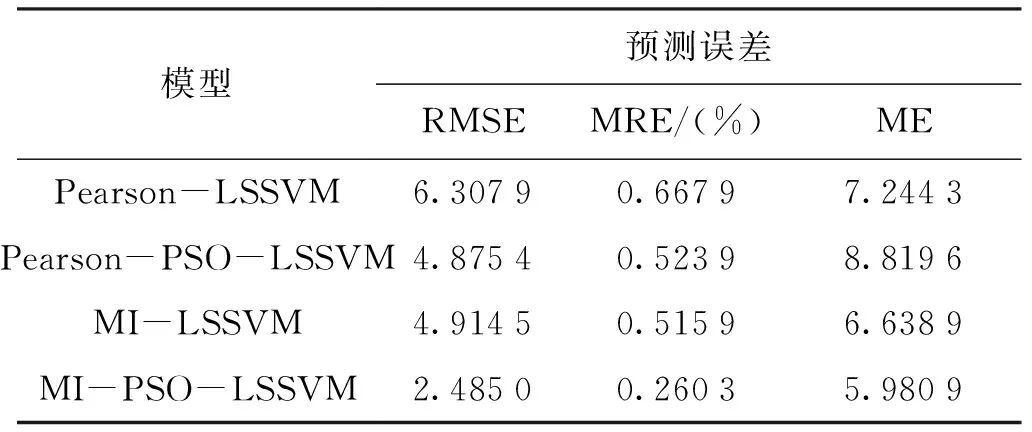
表3 不同模型误差对比Tab.3 Comparison of different model errors
6 结 论
本文提出了基于互信息的PSO-LSSVM模型预测二氧化硫浓度的方法,通过互信息与mRMR结合的方法筛选出的18个与主导变量相关性较大的辅助变量作为模型的输入,减少了辅助变量,降低了算法的复杂性。通过粒子群(PSO)算法对LSSVM模型参数寻优提升了模型的预测精度。对比LSSVM与PSO-LSSVM两种模型的仿真结果,可以发现本文所提出的模型预测精度更贴近实际值,误差小于未经寻优的LSSVM模型。
