基于改进半阈值迭代算法的ECT图像重建
2021-06-28刘一斐刘亚楠
马 敏,刘一斐,刘亚楠
(中国民航大学 电子信息与自动化学院,天津 300300)
1 引 言
电容层析成像(electrical capacitance tomography,ECT)技术问世于20世纪80年代中期。由于其具有非侵入性、安全性、响应速度快、安装便捷以及成本低廉等优点,并且与传统的仪器仪表相比较,电学层析技术具有更高的检测水平,所以ECT技术得到了国内外相关研究人员的广泛关注,并应用于国民经济多个领域[1~3]。
ECT技术在成像的过程中主要分为正问题和反问题[2],本文着重于反问题的讨论。一般在求解数学物理反问题的过程中,有两个实际的困难:一是原始数据可能与所论问题无关,则经典意义下的近似解可能不存在;二是原始数据中小的观测误差会导致近似解与真实解严重偏离,因而反问题常常是不适定的,很难得到合理的解答与答案。在ECT技术中成像是通过将测量得出的所有电极对之间的电容值作为投影数据,并根据被测区域电磁场分布形成的灵敏度矩阵,利用两者反演出场域内各相的介电常数分布[4]。由于ECT传感器提供的数据(受电极数目限制)远少于成像像素数目,导致ECT成像质量偏低,分辨率较差,具有严重的欠定性问题[5]。
因此在重建图像的过程中运用合适的图像重建算法尤为重要。目前已知的典型重建算法大部分是基于l2-范数的的凸优化算法,其特点是通过平滑图像使求解稳定,并没有产生更稀疏的解,导致图像分辨能力较差[7]。为了得到更加稀疏的解,本文将压缩感知理论[8]引入ECT图像重建当中,进一步提高了图像分辨能力。
由于传统信号的采集与传输需要满足奈奎斯特(Nyquist)采样定理,即采样频率必须大于原始信号最高频率的2倍,这样能够有效恢复原始信号,保证信息的高效传输。2006年,加利福尼亚理工学院的Candes E等人证明了:在图像的傅里叶表示中,若含有K个非零傅里叶系数,满足系数个数M≥2K,就可以将原始图像准确重构出来[9~11]。同年,斯坦福大学Donoho D L,以及加州大学的Tao T等在稀疏表示的基础上,将压缩和采样过程进行了合并,压缩感知理论应运而生。压缩感知理论包括3个步骤:1) 信号的稀疏表示;2) 设计测量矩阵,要在降低维数的同时保证原始信号x的信息损失最小;3) 设计信号恢复算法,利用M个观测值无失真地恢复出长度为N的原始信号。
近年,压缩感知理论被应用到图像处理、频谱分析、人脸识别、无线通信以及生物医学等众多领域,在电容层析成像领域的研究成果主要有:
2013年,吴新杰提出一种基于CS理论的ECT流型辨识方法,根据待测样本和标准样本稀疏解之间的线性相关程度来确定归属流型,为ECT流型辨识技术的研究提供了一种新的手段[12]。
2014年,王琦在ECT/CT双模态成像中引入了压缩感知理论,建立了一种随机采样模型,并结合相应的l1正则化算法进行动态成像,通过具体实验得到了多相流介质分布的真实情况[13]。
2017年,张立峰利用FFT基进行图像灰度的稀疏化;并基于高斯随机方法设计了ECT系统的观测矩阵;最后计算相应的雅可比矩阵;研究了基于内点法、GPSR算法以等CS重建算法,进行ECT图像重建[14,21]。该文首先选取了合适的稀疏基将原始灰度信号转化为相应的稀疏信号;其次针对ECT系统中灵敏度矩阵与稀疏基不相关性较弱的问题,基于高斯随机阵对灵敏度矩阵的各行重新排列,随后进行SVD分解,并加入修正因子得到了列独立性更高的观测矩阵;最后,采用基于l1/2-范数的半阈值迭代算法对ECT逆问题进行求解,考虑到惩罚项在原点处并不光滑,于是在罚函数中又加入了l2约束项,改善了原有算法在原点处的光滑性。通过改进的半阈值迭代算法求解,既缩小了图像误差又兼顾了成像速度,验证了本文所提算法在ECT成像过程中的可行性与优越性。
2 压缩感知理论
2.1 信号的稀疏表示
信号的稀疏性可以简单理解为信号向量具有较少的非零元素,一般的真实信号并非绝对稀疏,而是在某个变换域下近似稀疏,这样的信号称为可压缩信号。
假设在RN空间中存在一组向量基φi,构建一个基矩阵Ψ=[φ1,φ2,…,φN],在其上存在一个具有稀疏度K(即有K个非零值)的采样信号x,x∈RN,即
(1)
式中:α为X在Ψ域上的稀疏表示,α的稀疏度为k,若存在k≤K≪N,则说明x是稀疏的(即可压缩的),Ψ则称为信号x的稀疏基。要使信号的稀疏度尽可能减少,需要选取恰当的稀疏基。
本文的研究对象为ECT系统,需要对管道中的气固两相流进行图像仿真重建,初始信号选择被测管道中的图像灰度信号,该信号包含众场域介质分布信息并非稀疏信号,根据压缩感知理论,需要找到合适的稀疏基将初始灰度信号变为稀疏信号。
常见的稀疏基有离散余弦变换基(DCT)、离散正弦变换基(DST)、离散傅里叶变换基(DFT)将LBP算法获得的灰度矩阵作为初始信号矩阵,经不同的稀疏基处理之后效果如图1所示。
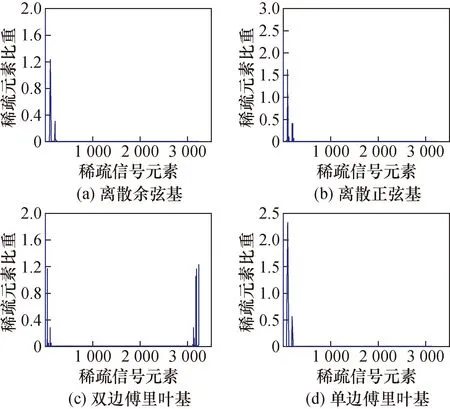
图1 不同稀疏基的稀疏效果图Fig.1 Sparse effects of different sparse matrix
横坐标表示为原始信号经稀疏基稀疏后的有用信号数量,纵坐标表示为有用信号的数值。以矩阵零范数度量信号的稀疏度,稀疏度在55~78,稀疏效果大致相同。离散余弦变换相当于一个长度大概是它两倍的离散傅里叶变换,由于实偶序列的DFT基是实对称的,因此数据存在一半的冗余[15]。注意到本文的初始灰度信号并非实偶矩阵,经过FFT基变换之后会产生虚数,从而对重构算法的要求更高。同DST基相比,DCT基的稀疏效果更好,因此本文选择DCT基作为初始信号的稀疏基。
2.2 观测矩阵与重构算法
观测器的采样目的是在获得M个观测值的情况下,同时保证其可以输出一个长度为N的的信号x对于信号测量的过程可以记为:
y=Φx
(2)
式中:Φ∈RM×N表示为观测矩阵,在ECT系统中则为灵敏度矩阵;y为观测值(即电容值)。
如果x是稀疏的,则按照式(1)将x变换到Ψ域,式(2)可写成:
y=Φx=ΦΨα
(3)
选取非相关性作为ECT系统中灵敏度矩阵的优化准则。因此,需要在灵敏度矩阵的基础上进一步增大与稀疏基的不相关性,同时提高灵敏度矩阵的列独立性。
考虑到高斯矩阵与大多数的稀疏基并不相关,如果将灵敏度矩阵的各行按照高斯随机顺序重新排列[14],便可以增大灵敏度矩阵与稀疏基的不相关性,对应的电容矩阵也做相同变换,因此选取非相关性作为ECT系统中灵敏度矩阵的优化准则,将灵敏度矩阵的各行按照高斯随机顺序重新排列,并引入截断奇异值的思想[16],增大奇异值中较小的数值,对变换后的灵敏度矩阵进行奇异值分解重新得到:
y=S1Ψα=Aα
(4)
式中:y表示变换后的电容矩阵;S1表示变换后的灵敏度矩阵即新的测量矩阵;Ψ代表稀疏基;A=S1Ψ代表观测矩阵;α是初始灰度信号G0变换后的稀疏向量。
对于式(4)的求解过程称为算法的重构,转换为如下形式:
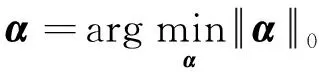
s.t.y=Aα
(5)
由于l0-范数的求解过程是把重构信号α的非零项位置逐一列出,利用线性组合求解,是一个NP-hard问题。通常将其转化为其他替代模型利用不同的重构算法进行求解。
3 l1/2正则化的半阈值迭代算法
针对y=Aα此类具有欠定性特点的优化求解问题,利用lp代替l0构建新的泛函模型,并且p取0.5,则基于l1/2正则化[17]的泛函模型如下:
(6)
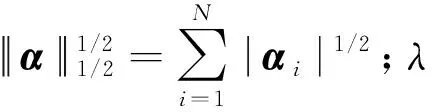
(7)
αn+1=H1/2(α+μAΤ(y-Aα))
(8)
H1/2(·)代表阈值函数,设其自变量Bμ(α)=α+μAΤ(y-Aα),存在正实数阈值t*>0使得下式成立:
(9)
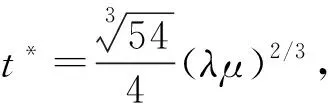
(10)
g(Bμ(α))=
(11)
文献[18]中提出若用Bμ(α)k代表Bμ(α)进行降序排列的第k个值,据此求得λ的取值范围:
(12)
根据文献[19]中的经验值,参数λ被确定为:
(13)
4 l1/2正则化的改进半阈值迭代算法
考虑到l1/2正则子在α=0处并不是光滑的,需要对罚函数项进一步约束,在原点处加入了更加平滑的l2约束项,对式(11)进行修改,重新构建基于非凸正则子的ECT模型:
(14)
根据据第3节中的步骤重新计算一阶最优性条件,并加入稀疏信号变换可得:
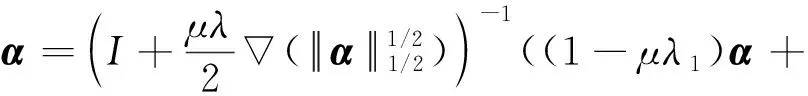
(15)
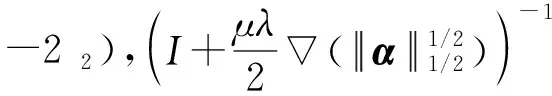
(16)
于是得到原点处的迭代公式:
(17)
根据文献[20],原点处的优化计0算结果如下:
(18)
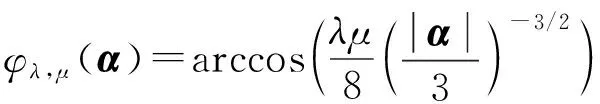
(19)
λ1为l2-范数优化约束下的正则化参数,在ECT系统中,通常情况下按照经验值取λ1=0.000 3。基于l1/2正则子的参数λ可利用交叉验证法进行选取,将Bμ(α)代入式(10)中,可知存在半阈值函数需满足:
(20)
若用Bμ(α)k代表Bμ(α)进行降序排列的第k个值,并结合ECT系统中的数据计算,进一步可得λ=0.001 5。
如果ε代表一个较小的常数值,改进的半阈值迭代算法最终可写成如下形式:
(21)
ECT系统中基于l1/2正则化的半阈值迭代算法求解步骤如下:
1) LBP算法得到的灰度矩阵作为初始矩阵,并采用DCT基进行稀疏化;
2) 将灵敏度矩阵S的各行向量按高斯随机顺序重排,随后进行奇异值分解,加入修正因子增大观测矩阵的奇异值,从而得到优化后的观测矩阵;
3) 改变罚函数,构建基于l1/2正则化的ECT图像优化模型;
4) 初始化,设置初始迭代矩阵为零矩阵;
5) 采用半阈值迭代算法对优化模型进行求解;
6) 结合匹配追踪策略,加速迭代收敛过程;
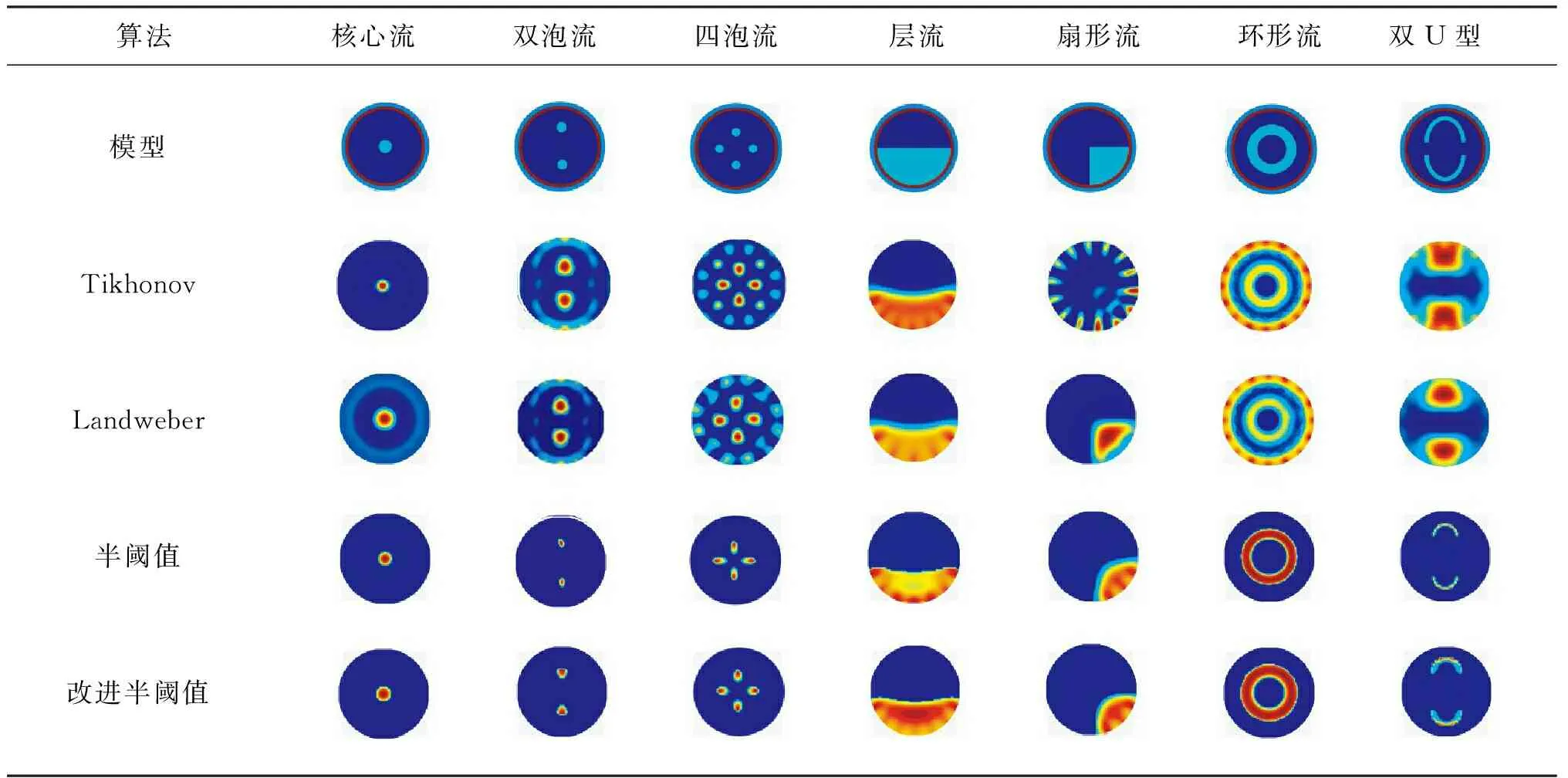
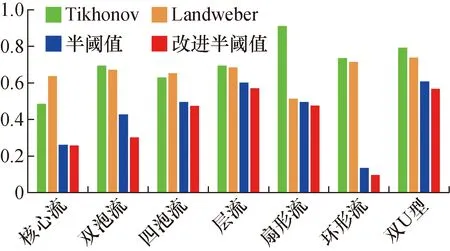
7) 设置迭代终止条件α(k+1)-α(k) 8) 将精确解α*代入G=ΨDCTα*得到重建后的图像灰度信号。 基于改进半阈值迭代算法流程图如图2所示。 图2 基于l1/2正则化的改进半阈值迭代算法的流程图Fig.2 Diagram of improved half threshold iterative algorithm based on l1/2 regularization 在实验仿真的过程中,将LBP算法获得的灰度矩阵作为初始信号矩阵,选择DCT基作为初始信号的稀疏基对初始信号进行稀疏;将灵敏度矩阵的各行按照高斯随机顺序重新排列,并引入截断奇异值的思想,增大奇异值中较小的数值,从而得到新的奇异值矩阵和观测值,重新建立了基于压缩感知理论的ECT图像重建问题。 本次仿真使用COMOSL 5.5软件对16电极管道的ECT传感系统建模,空场中材料(空气)的相对介电常数设置为1.0;电极和屏蔽罩(铜)的相对介电常数设置为2.2;管道材料(塑料)相对介电常数设置为5.8;管道内被测物体的相对介电常数设置为3.0。分割网络设置为64*64,共3 228个有效单元。利用MATLAB 2014a进行图像重建和评估,仿真流型选择核心流、二泡流、四泡流、层流、扇形流、环流和双U型。 不同算法的仿真成像效果如表1所示。 表1 改进半阈值算法与其他算法成像效果对比Tab.1 Comparison of image effect of improved half threshold algorithm and other algorithm 选取直接算法中的Tikhonov正则化、迭代类算法中的Landweber和基于压缩感知理论的半阈值迭代类算法进行对比实验。 比较不同算法成像效果可得:ECT典型成像算法中的Tikhonov正则化和Landweber迭代算法在泡状流和层流中的成像效果较好,但是受到周围电极影响,图像会产生明显的粘连以及伪影现象;在环形、双U型中成像效果较差,无法正确分辨被测物体的实际形状和大小。半阈值迭代算法在各个流型中均不会产生伪影和粘连现象,几乎可以完整复现被测物体的实际位置和形状,但是在多泡流中所呈现图形的大小稍有欠缺。而改进的半阈值迭代算法同上述传统的算法相比可以有效改善多泡流中的伪影粘连现象,与半阈值迭代算法相比可以更准确复现被测物体的位置和大小。 为了更加客观地评价不同算法的成像效果,定量反映成像质量的优劣,选取图像误差(image error,IME)和图像相关系数(correlation coefficient,CORR)作为评价指标,并计算了算法运行时间。 (22) (23) 表2 不同算法的图像误差Tab.2 Image error of different algorithms 表3 不同算法的图像相关系数Tab.3 Image correlation coefficients of different algorithms 表4 不同算法的成像时间Tab.4 Imaging time of different algorithms s 通过分析表2~表4可得:大多数流型中,Landweber迭代算法成像时间最长,Tikhonov正则化算法次之;所有流型中,半阈值迭代算法最短,改进半阈值算法与半阈值时间相近。同时Landweber迭代算法和Tikhonov正则化法图像误差相差不大,但Tikhonov正则化的实时性更好。半阈值迭代算法相较于传统的算法,图像误差较小,成像的精度更高,而且成像速度更快,即使与非迭代算法中的Tikhonov正则化相比,成像时间也仅为后者的六分之一,改进后的半阈值迭代算法,虽然成像时间稍微有所增加,但是在一定程度上减小了图像误差,且成像时间仍旧比其他算法的量级小很多,从图3~图5可以更直观看出改进半阈值迭代算法的优势。综合考虑系统实时性和重建质量的要求,改进半阈值迭代算法的优势更为明显,改进的半阈值迭代算法与所有对照组的对比结果最优,证明了该算法在求取稀疏解时强大的寻优能力。 图3 各算法图像误差图对比Fig.3 Comparison of image error of each algorithm 图4 各算法图像相关系数对比Fig.4 Comparison of image correlation coefficient of each algorithm 图5 各算法图像成像时间对比Fig.5 Comparison of imaging time of each algorithm 电容层析成像逆问题的求解存在欠定性和病态性,传统的直接算法和迭代类算法往往无法兼顾求解速度和成像质量。本文将压缩感知理论引入ECT成像逆问题的研究中,通过稀疏化初始信号、重构观测矩阵以及重构算法等过程完成了ECT图像重建的任务,有效改善了系统的欠定性问题。通过对ECT系统的泛函模型进行修正,采用改进的半阈值迭代算法求解,精确复现了初始信号,且系统具有较好的实时性。同传统算法和部分压缩感知中的算法相比,成像精度较高,同时能够兼顾成像速度,显示出本文所提算法在ECT系统中的良好应用。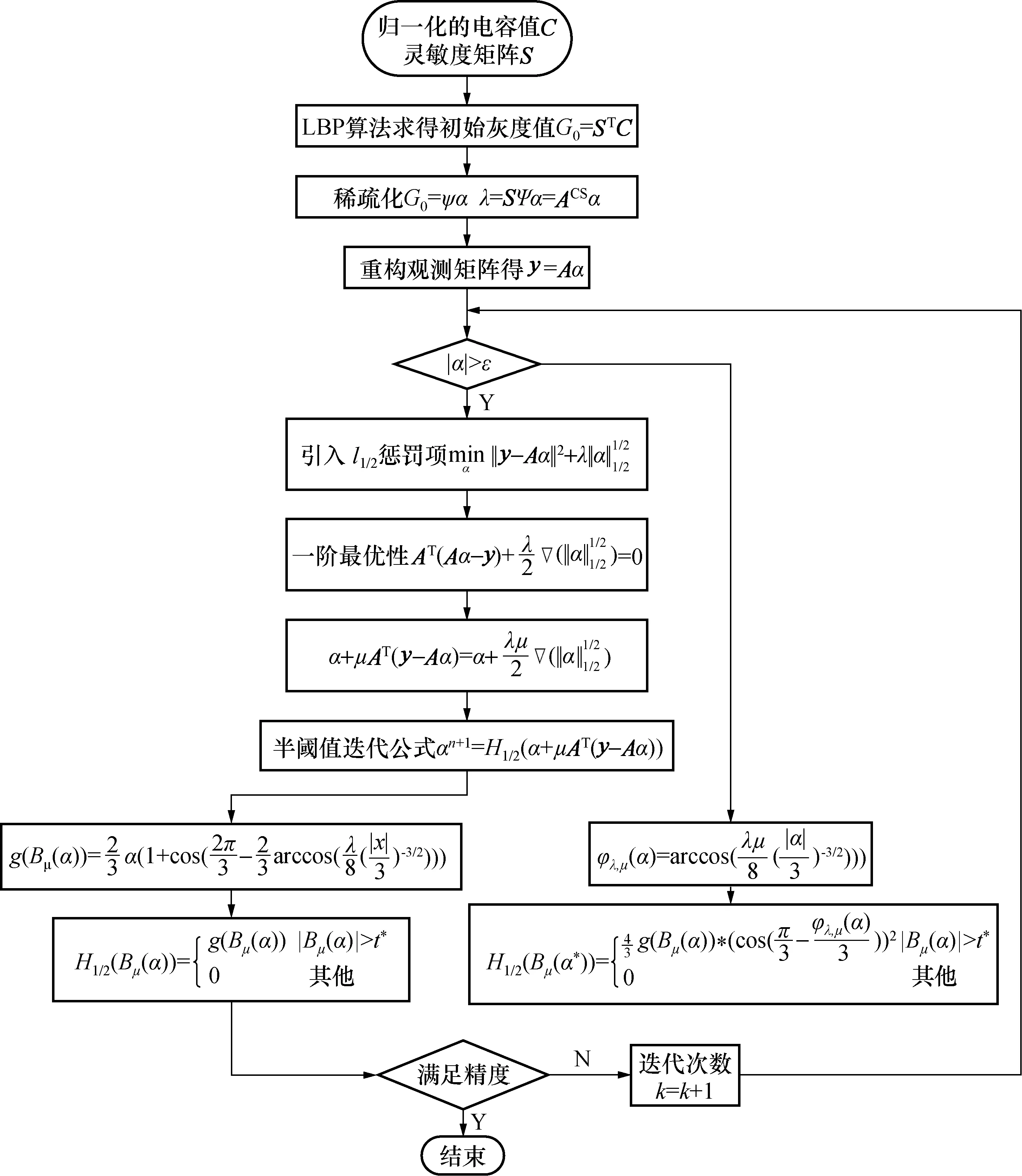
5 算法成像效果
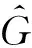
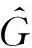



6 结 论
