基于深度循环神经网络的协作机器人动力学误差补偿
2021-06-28汪火明侯至丞杨文林梁济民
徐 征,张 弓✉,汪火明,侯至丞,杨文林,梁济民,王 建,顾 星
1) 广州中国科学院先进技术研究所机器人与智能装备中心,广州 511458 2) 中国地质大学机械与电子信息学院,武汉 430074
准确的机器人动力学模型是搭建仿真模型,验证先进控制算法和对控制系统进行深度分析的基础[1-2].随着对机器人动态性能要求的提高和协作机器人概念的兴起,常规无模型控制方法,如PID算法不仅轨迹跟踪精度较低,抗干扰能力较差,尤其无法实现碰撞检测、柔顺控制等人机交互功能[3].
对于多轴串联机器人进行动力学建模一般会考虑重力、科里奥利力、惯性力和摩擦力等主要因素,但是对于较复杂的特性,例如减速机柔性、连杆弹性、摩擦力随工况的变化、电机转子惯性力等,较少建立其数学模型[4-5],从而导致计算力矩与实际力矩误差较大,阻碍了协作机器人碰撞检测、拖动示教和柔顺控制的良好实现.有学者对此进行了研究,文献[6-8]各自建立了摩擦特性模型并提出了针对性的补偿方法,也有采用机器学习方法的,如利用反向传播(Back propagation,BP)神经网络[9]和径向基函数(Radial basis function,RBF)网络进行拟合或补偿[10-11],有些也提出了对应的控制方法[12],但鲜有研究对各种复杂特性综合起来考虑的.
对于参数辨识技术,有解体测量计算方法[13-14]、解体实验测量法[15-16]、不解体实验测量方法[17-18]和理论辨识[19]等方法.解体方法无法或难以计算机器人关节特性[20],理论辨识法得到的惯性张量矩阵在任意形位上不一定是正定的,实际中也不可能存在,其控制也不稳定[21].
为此,本文提出利用深度循环神经网络对协作机器人动力学模型进行误差补偿,首先建立动力学方程,然后采用不解体实验测量方法结合最小二乘法对其中参数进行辨识.接着,针对协作机器人的未建模特性或建模不精确的问题,采用深度循环神经网络进行补偿,以减小动力学模型误差并提高力矩预测精度.最后在实验中,以电机电流等效作为关节力矩信号,把电机电流和电机常数的乘积作为输出轴力矩,同时结合摩擦力模型计算得到机器人关节的输出力矩,代替价格高昂且安装不便的力矩传感器,以完成补偿方法的实验验证.
1 协作机器人动力学模型
本研究基于自主研发的六自由度协作机器人,图1和图2分别为其三维模型图和Denavit-Hartenberg(D-H)模型图,从图中可以看到轴 2、3、4的相互平行,逆运动学存在封闭解.考虑重力、科里奥利力、惯性离心力和摩擦力,采用欧拉-拉格朗日法计算关节力矩,得到机器人刚体动力学方程:


图 1 协作机器人三维模型图Fig.1 3D model of the collaborative robot

图 2 协作机器人D-H模型图Fig.2 D-H structure of the collaborative robot
式中:q为关节角向量;为关节角速度向量;为关节角加速度向量;M(q)为机械臂惯性矩阵;H(q,)为离心力和科里奥利力矩阵;G(q)为重力矩阵;τf为摩擦力项.
机器人关节的减速机、轴承等带来的摩擦影响较大[15],导致角速度换向处,即在速度零点附近,计算力矩相对实际误差较大.针对该现象,采用Stribeck摩擦力模型对关节摩擦机械建模,其摩擦力矩为:
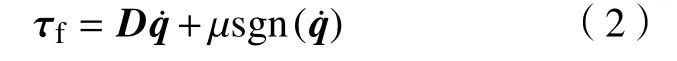
式中:D为 黏滞摩擦系数矩阵;μ为库伦摩擦系数.
综合式(1)和(2),可以得到方程:
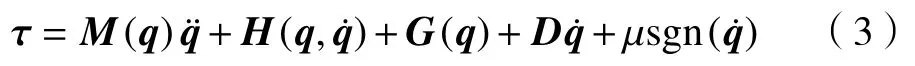
故方程(1)可改成如下线性形式:


式中:Φr为重组后的观测矩阵;θr为最小惯性参数集向量.
对于模型精度,本文以预测力矩(计算力矩)相对于实际测量力矩的均方根误差作为评价标准.若均方根误差较小,则说明模型精度高,反之则精度较低.
2 激励轨迹生成
不解体实验测量方法需要驱动机器人运动以获取数据,考虑到计算精度和实验可行性,机器人运动轨迹即激励轨迹需要满足多种条件.六轴机器人动力学运算复杂度高,在辨识后三轴的动力学参数时可以锁定前三轴单独实验,辨识的难度大大降低,更具针对性且减小了运算量[16].限于篇幅和运算量,本文仅对协作机器人末端轴4至轴6的动力学参数进行了辨识和研究.实验采用傅里叶级数前五项,即式(5)作为激励轨迹.由于是周期函数,便于重复多次进行该实验,同时与驱动器通信采集位移、速度和电流等信息.

式中:qi(t)∈Rn为关节i在关节空间中的轨迹关于时间t的函数;ωf是基频;qi,0(t)∈Rn为常量偏移;每条轨迹包含11个参数,即ai,k,bi,k,qi,0和ωf=1.
激励轨迹的优劣与观测矩阵抑制噪声的能力和其病态性息息相关,直接影响辨识参数的精度,这里通过观测矩阵W的条件数来定义目标函数:

式中:Cond(W)=σmax(W)/σmin(W),σmax(W)和σmin(W)分别为W的最大和最小奇异值.
目标函数值越小,则辨识参数 θ对测量误差的敏感度越低,实验辨识得到的参数精度就有可能更高.同时还要考虑实际机器人有运动性能的限制,以运动范围、起始和停止阶段的速度和加速度为约束,则该激励轨迹优化问题可描述为:

式(8)是一个非线性多约束的优化问题,可以采用NSGA等目标优化算法[22]对其进行优化,得到优化后的激励轨迹如图3所示.三张图中,横轴均为时间,纵轴依次为角位移,角速度和角加速度.从图中可以看出,轨迹变化平滑,起止点均为零,运动幅值较大,但也未超出限制范围,该优化后的激励轨迹将用于第4节的实验研究.
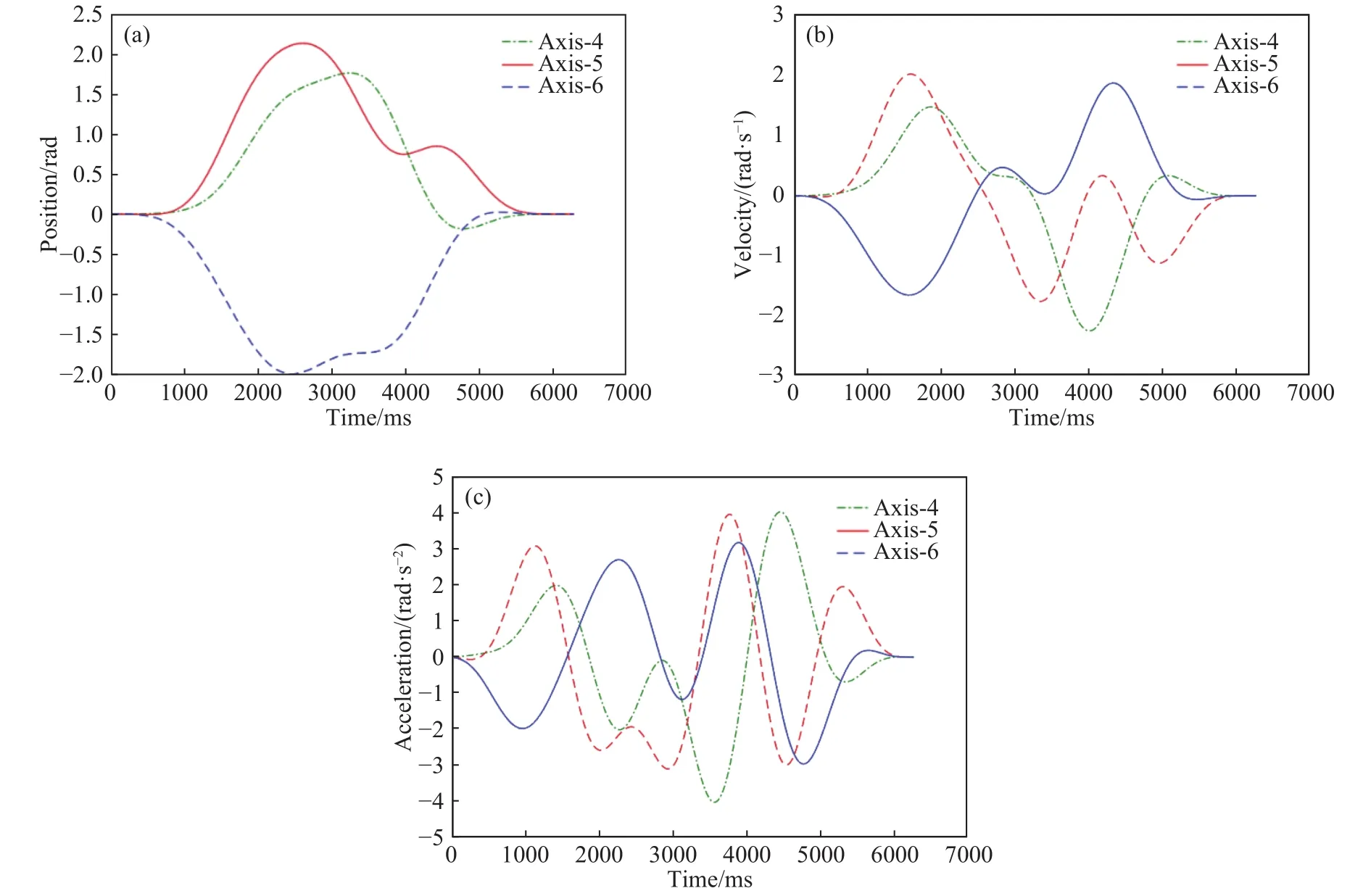
图 3 参数辨识所用激励轨迹.(a)位移;(b)速度;(c)加速度Fig.3 Excitation trajectory for parameter identification: (a) position; (b) velocity; (c) acceleration
3 深度循环神经网络误差补偿
循环神经网络(Recurrent neural network,RNN)是一类用于处理序列数据的神经网络,其中的长短期记忆(Long short-term memory,LSTM)单元网络相比于普通的人工神经网络,解决了早期RNN网络存在的长时期依赖,梯度爆炸和梯度消失等问题[23-24],在对历史信息的保留和对未来信息的预测上有较大进步.本研究将进一步探索LSTM在机器人动力学方面的应用.
机器人运动学和动力学数据在时间上连续相关,且摩擦力的记忆特性和电机参数随温度变化带来的时变特性,采用LSTM网络可以很好地补偿这些因素.本研究采用具有细胞状态和门控结构的LSTM细胞单元以期实现较好的补偿效果.
如图4所示,LSTM细胞单元增加了细胞状态向量C和相关的门控结构,以控制遗忘和记忆的方法较好地解决了普通RNN Cell存在的梯度爆炸和梯度消失问题.其前向运算过程为:


图 4 LSTM隐含层细胞结构Fig.4 LSTM cell of hidden layer
式中:σ为 sigmoid函数;ft为遗忘门输出量;Wf,Wi、WC和Wo依次为遗忘门、输入门、更新状和输出门状态参数;bf,bi、bC和bo依次为遗忘门、输入门、更新状和输出门状态的偏移量;C和h分别为细胞输出向量和隐含状态,x为输入向量,i和为细胞更新状态中间变量,o为输出门中间变量,以上各变量下角标为时间序列编号.
LSTM网络训练过程采用是随时间反向传播算法 (Back propagation trough time,BPTT),与经典的反向传播算法类似,包括前向计算、反向计算、计算梯度、更新参数等步骤.
其中基于梯度的优化算法种类众多,本文选用适应性动量估计(Adaptive moment estimation,Adam)算法[25].该算法是一种有效的基于梯度的随机优化方法,能够对不同参数计算适应性学习率且占用存储资源较少,相比于其他随机优化方法,Adam算法在实际应用中整体表现更优.
综上所述,提出如图5所示的技术框架,包括LSTM网络、数据集的产生、网络训练手段等.其中网络的输入和输出层为全连接网络,隐含层由LSTM细胞单元组成,其中x为分批数据,C为细胞输出,H为细胞隐含状态,P为每层网络输出,角标L为网络层数,Compensation value是实际力矩和计算力矩的差值.其主要步骤为:
(1)原始数据(位移、速度、加速度、力矩)采集;
(2)原始数据(位移、速度、加速度)经未补偿动力学模型计算得到预测力矩;
(3)原始数据和预测力矩经过归一化操作,分为训练集和测试集;
(4)训练集进入全连接的输入层;
(5)经过包括64个LSTM节点的隐含层迭代计算(依次计算每个细胞输出);
(6)经过输出层输出经网络补偿后的力矩值;
(7)损失为预测力矩(计算力矩)相对于实际测量力矩的均方根误差;
(8)以该损失最小采用Adam优化器对网络参数迭代优化;
(9)反向计算每个LSTM细胞的误差项,包括按时间和网络层级两个反向传播方向;
(10)根据相应的误差项计算每个权重的梯度;
(11)应用更新权重;
(12)测试集经过网络计算出经补偿后的预测力矩,评估补偿效果.
网络由开源机器学习平台Tensorflow1.15.0实现,根据经验和实际情况,确定网络主要超参数如表1所示.

表 1 网络主要超参数值Table 1 Hyperparameters of the net
其中输入向量依次包括4、5和6各轴的计算力矩、历史各时刻实际力矩、实际速度和实际位移.输出向量依次包括4、5和6各轴的下一时刻预测力矩.网络的节点数则根据特征维度和数据量进行选择,损失即为下一时刻预测力矩相对于下一时刻实际力矩的均方根误差,即:
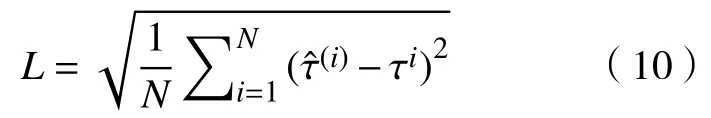
式中:N为数据集样本数量,实际为机器人连续运动量的采样点数量;(i)为预测力矩值;τi为实际力矩.
数据集来源于激励轨迹驱动下的机器人实际采集的数据,可分为两部分:训练集Ftr和测试集Fte.对于训练集,激励轨迹即是第3节中得到的最优激励轨迹;对于测试集,可以通过增加新约束条件的方法再产生一条新的激励轨迹.在式(6)的基础上增加约束:qi(t=3.8)=0,得到测试集轨迹如图6所示.
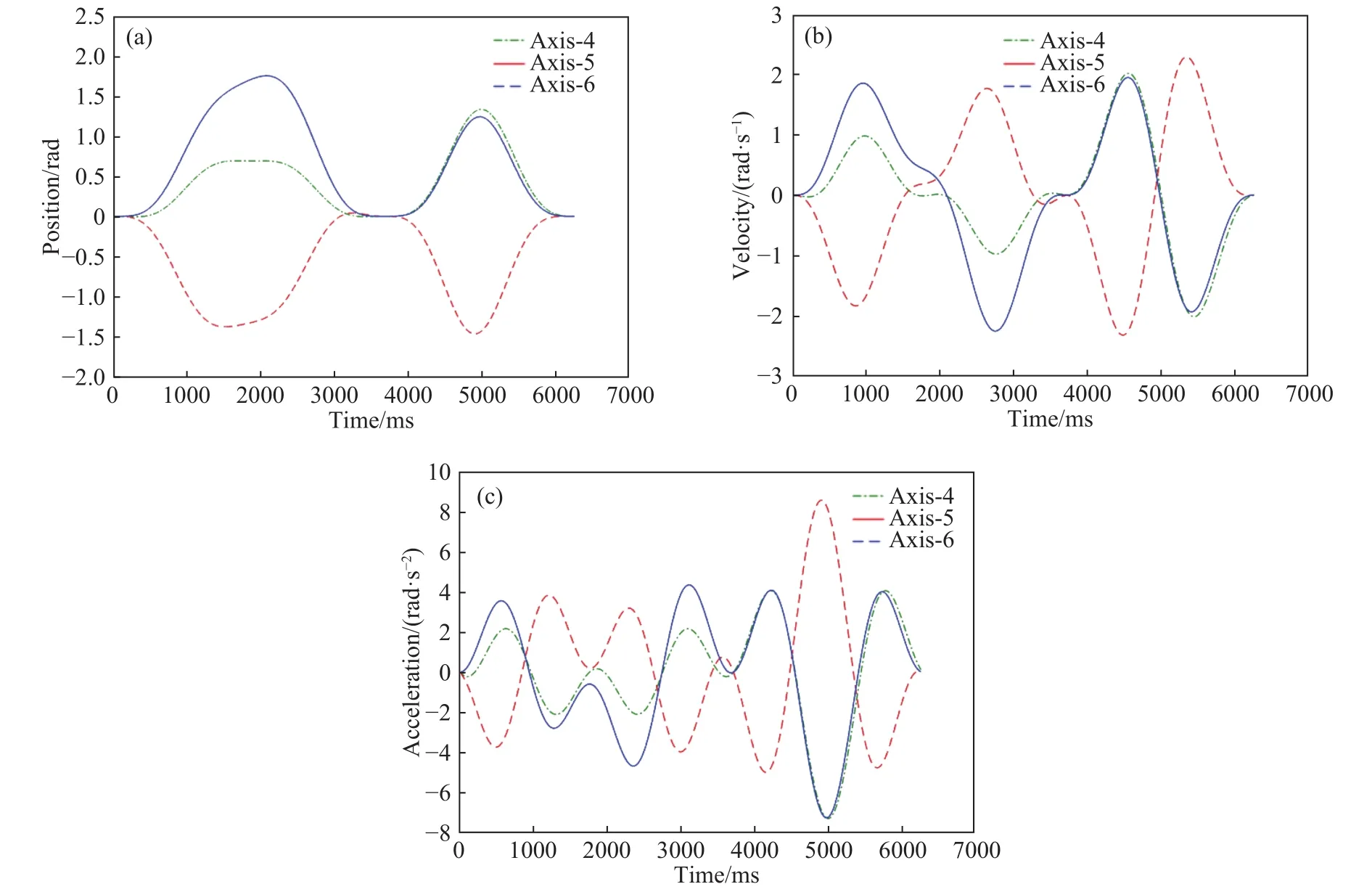
图 6 测试集的激励轨迹.(a)位移;(b)速度;(c)加速度Fig.6 Excitation trajectory of test set: (a) position; (b) velocity; (c) acceleration
从图6中可以看出,测试集曲线各处平滑连续,运动幅值较大,但也未超出限制范围,相比于图3的训练集曲线,图6中的各轴位移曲线具有两个显著分开的波峰,运动中存在一个零点,且速度和加速度也有较大差异,可在充分利用机器人性能的同时测试网络的泛化能力.同时,运动过程中的零点便于在实验中核对误差,起到监控机器人工作状态的作用.
下一步的工作,如网络的训练,需要实验数据的支撑,故在下一节实验部分继续进行.
4 实验结果
本次实验仅对该机器人末端的轴4、轴5和轴6进行分析和实验.由于靠近末端的轴4至轴6三轴力臂相对较短,质量相对较小,惯性和重力矩相对较小,摩擦力和电机转子惯量等未精确建模的特性会带来更大的相对误差,因此误差补偿技术具有较大的实际应用价值.
实验中,各轴电机伺服驱动器与控制器由EtherCAT连接通信,驱动器置为周期性位置模式,控制器以100 Hz固定频率发送图3和图6的激励轨迹至驱动器,保证整个运动过程连续流畅.由于只研究轴4至轴6的动力学特性,轴1至轴3的位移指令始终为零.
网络的训练采用上述的激励轨迹与实验数据为训练数据集,以理论计算力矩和实际力矩的均方根误差为损失函数,训练目标即为该损失函数最小.随着网络训练次数增加,损失逐渐减小,如图7所示.

图 7 网络训练步数与均方根损失Fig.7 Epochs vs RMS loss
图8和图9分别为测试集激励轨迹下,补偿前和补偿后轴5的实际力矩、预测力矩和误差曲线,可以明显看到经过LSTM补偿后的动力学模型对力矩的预测误差相比未经补偿的有显著提高,各轴补偿前后预测力矩与实际力矩的均方根误差如表2所示.从图表中可以看出,补偿后的动力学模型对力矩具有良好的预测效果,轴4至轴6预测力矩(理论计算)与实际力矩的均方根误差,相比于传统模型分别降低了66.5%、78.9%和61.8%.这是由于协作机器人轴4至轴6结构轻巧,惯性力和重力较小,因此摩擦力等未建模或未能精确建模的因素影响占比很大,造成很大误差.
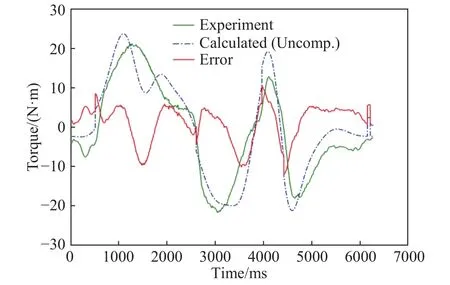
图 8 轴5计算力矩(未经补偿)、实际力矩和误差Fig.8 Calculated torque (uncompensated), real toruqe, and errors of axis-5

图 9 轴5经过LSTM网络补偿后的计算力矩、实际力矩和误差Fig.9 Calculated torque with LSTM compensation, real torque, and errors of axis-5

表 2 各关节计算力矩相对实际力矩的均方根误差Table 2 RMS error of calculated torque between real value
5 结论
为了解决协作机器人动力学模型难以建立与辨识,导致机器人计算预测力矩误差较大的问题,本文针对自主研发的六自由度协作机器人,首先建立了一般的机器人动力学模型,然后生成了优化后的激励轨迹并进行了相关实验.同时,在此基础上采用深度循环神经网络中的长短期记忆模型对模型预测力矩和实际力矩之间的误差进行了补偿.结论如下:协作机器人轴4至轴6结构轻巧,惯性力和重力较小,摩擦力、转子惯性力等未建模或未能精确建模的因素影响占比很大,依靠一般动力学方程计算预测力矩有较大误差.采用深度循环神经网络中的长短期记忆模型可有效补偿动力学模型误差.实验表明轴4、5和6的预测力矩与实际力矩的均方根误差与传统模型相比,分别下降了66.5%,78.9%和61.8%.由此可见,基于循环神经神经网络的误差补偿技术是可行和有效的,可为后续的动力学控制研究提供良好的基础.
